2.1. Probability Theory and Stochastic Processes in RL link

Probability theory is the mathematical cornerstone of reinforcement learning (RL), providing the tools to model and reason about uncertainty in complex, dynamic systems. Just as a sailor navigates uncharted waters using probabilistic predictions of wind and current, RL agents rely on probability theory to make informed decisions in environments with unknown or stochastic dynamics. Central to this theory is the concept of a random variable, which acts as a mapping from the outcomes of random experiments to numerical values that describe those outcomes. This abstraction enables us to quantify and work with uncertainty in a mathematically rigorous way.

Figure 1: Key use cases of probability theory in Reinforcement Learning.

Consider the example of flipping a biased coin, which can represent an RL agent's decision-making process when selecting between two actions, such as turning left or moving forward. This scenario can be captured by a discrete random variable $X$, which takes values in the set $\{0, 1\}$ corresponding to the possible outcomes. The probabilities associated with these outcomes, $P(X = 0) = p$ and $P(X = 1) = 1 - p$, define the agent's inclination towards each action. Much like meteorologists use probability distributions to predict the likelihood of rain or sunshine, RL uses similar constructs to anticipate and respond to environmental feedback.

Expanding the analogy further, think of an RL agent as a chess player deliberating its next move. Each potential action, from moving a pawn to sacrificing a queen, is governed by a probability distribution reflecting the expected payoff or utility of that action. Probability theory allows the agent to model both the immediate outcomes of its actions and their longer-term consequences, capturing the inherent randomness in its environment and the uncertainty about future states. For example, the randomness might stem from unpredictable environmental transitions, such as an opponent's move in chess or a gust of wind altering a drone's trajectory.

Moreover, probability theory forms the backbone of key RL components, such as Markov decision processes (MDPs), where state transitions and rewards are modeled probabilistically, and Bayesian inference, which allows agents to update their beliefs about the environment as they gather new information. It also enables the application of sophisticated methods like Monte Carlo simulations to estimate expected returns and stochastic gradient descent to optimize policy parameters.

In essence, probability theory not only equips RL with the ability to model and handle uncertainty but also provides the mathematical machinery to analyze, predict, and optimize outcomes in uncertain domains. It transforms the agent's decision-making from a blind trial-and-error process into a structured and adaptive strategy, much like how a seasoned explorer uses probabilistic maps to navigate uncharted terrain with confidence.

The behavior of a random variable is captured by its probability distribution. For discrete random variables, the probability mass function (PMF) $P(X=x)$ gives the likelihood of each possible value, while for continuous random variables, the probability density function (PDF) $f_X(x)$ provides the density of probabilities over the real numbers. The expectation, or mean, of a random variable quantifies its average outcome over an infinite number of trials and is given by:

$$ \mathbb{E}[X] = \begin{cases} \sum_{x} x P(X=x) & \text{(discrete case)} \\ \int_{-\infty}^\infty x f_X(x) dx & \text{(continuous case)} \end{cases}. $$

In reinforcement learning, conditional probability is used extensively to model dependencies between events. For example, the probability of transitioning to a new state $s'$ given a current state sss and action $a$ is written as $P(s'|s, a)$. This conditional dependency is the core of the state transition dynamics in RL. Another important tool is the law of total probability, which helps compute the marginal probabilities of events by summing over their conditional probabilities:

$$ P(B) = \sum_{A} P(B|A) P(A). $$

Stochastic processes extend probability theory to model systems that evolve over time. A stochastic process is a sequence of random variables $\{X_t\}_{t=0}^\infty$, where each $X_t$ represents the system’s state at time $t$. A crucial class of stochastic processes in RL is the Markov chain, characterized by the Markov property, which states that the future state depends only on the current state and not on the past history:

$$ P(S_{t+1} = s_{t+1} | S_t = s_t, S_{t-1} = s_{t-1}, \dots, S_0 = s_0) = P(S_{t+1} = s_{t+1} | S_t = s_t). $$

Markov chains are often represented by their transition matrix, $\mathbf{P}$, where $P_{ij} = P(S_{t+1} = s_j | S_t = s_i)$. Over time, a Markov chain may converge to a stationary distribution $\pi$, satisfying:

$$\pi \mathbf{P} = \pi,$$

where $\pi$ represents the long-term probabilities of being in each state.

Reinforcement learning extends Markov chains into the realm of decision-making using Markov Decision Processes (MDPs). An MDP includes a set of states $\mathcal{S}$, actions $\mathcal{A}$, transition probabilities $P(s'|s, a)$, and a reward function $R(s, a, s')$. The objective in an MDP is to find a policy $\pi(a|s)$ that maximizes the agent’s expected cumulative reward:

$$ G_t = \mathbb{E}\left[\sum_{k=0}^\infty \gamma^k R(S_{t+k}, A_{t+k}, S_{t+k+1})\right], $$

where $\gamma$ is the discount factor that balances immediate and future rewards. The MDP formalism provides the mathematical scaffolding for most RL algorithms.

The theoretical concepts of probability theory and stochastic processes are implemented practically in Rust to make them accessible and actionable. First, we demonstrate probability computations using the rand and statrs crates to generate random samples and calculate properties of distributions. This lays the foundation for stochastic modeling in RL. Next, we simulate a Markov chain using a transition matrix to observe state transitions and long-term behavior, capturing the dynamics over time. Finally, we construct a simple MDP in Rust, defining states, actions, transitions, and rewards to simulate decision-making under uncertainty.

The code snippet below generates random samples from a uniform distribution using the rand crate and calculates the mean of a normal distribution using the statrs crate. These computations serve as building blocks for more complex RL tasks involving random sampling and probabilistic reasoning.

[dependencies]
rand = "0.8.5"
statrs = "0.17.1"

use rand::distributions::{Distribution, Uniform};
use statrs::distribution::Normal;
use statrs::statistics::Distribution as StatrsDistribution;

fn main() {
    // Generate samples from a uniform distribution
    let uniform = Uniform::new(0.0, 1.0);
    let mut rng = rand::thread_rng();
    let samples: Vec<f64> = (0..10).map(|_| uniform.sample(&mut rng)).collect();
    println!("Uniform samples: {:?}", samples);

    // Compute the mean of a normal distribution
    let normal = Normal::new(0.0, 1.0).unwrap();
    let mean = normal.mean().unwrap(); // `mean` returns an Option<f64>, so unwrap() is used
    println!("Mean of normal distribution: {}", mean);
}

This implementation highlights the simplicity and power of Rust for handling probabilistic models. The generated samples can represent actions taken by an agent or outcomes of stochastic transitions, while the mean and other statistical properties can help analyze distributions of rewards or state transitions.

The following code simulates a Markov chain by defining a transition matrix and repeatedly sampling the next state based on the current state. This simulation demonstrates the dynamics of state transitions over time and provides insight into steady-state behavior.

use rand::distributions::{Distribution, WeightedIndex};

fn main() {
    let states = ["A", "B", "C"];
    let transition_matrix = [
        [0.1, 0.6, 0.3], // Transitions from state A
        [0.4, 0.4, 0.2], // Transitions from state B
        [0.3, 0.3, 0.4], // Transitions from state C
    ];

    let mut current_state = 0; // Start in state A
    let mut rng = rand::thread_rng();

    for _ in 0..10 {
        let dist = WeightedIndex::new(&transition_matrix[current_state]).unwrap();
        current_state = dist.sample(&mut rng);
        println!("Next state: {}", states[current_state]);
    }
}

The weighted probabilities in the transition matrix define how likely it is to move from one state to another, encapsulating the Markov property. Over repeated iterations, the chain evolves, and its long-term behavior can approximate the stationary distribution.

The final code defines a simple MDP, complete with states, actions, transition probabilities, and rewards. It simulates a single step of decision-making, showing how actions influence transitions and rewards.

use rand::distributions::{Distribution, Uniform};

struct MDP {
    states: Vec<&'static str>,
    actions: Vec<&'static str>,
    transition_probabilities: Vec<Vec<Vec<f64>>>,
    rewards: Vec<Vec<f64>>,
}

fn main() {
    let mdp = MDP {
        states: vec!["S1", "S2"],
        actions: vec!["A1", "A2"],
        transition_probabilities: vec![
            vec![vec![0.7, 0.3], vec![0.4, 0.6]], // Transitions for S1
            vec![vec![0.6, 0.4], vec![0.5, 0.5]], // Transitions for S2
        ],
        rewards: vec![
            vec![5.0, 10.0], // Rewards for actions in S1
            vec![3.0, 8.0],  // Rewards for actions in S2
        ],
    };

    let state = 0; // Start in S1
    let action = 1; // Take action A2
    let prob = Uniform::new(0.0, 1.0);
    let mut rng = rand::thread_rng();

    let transition = &mdp.transition_probabilities[state][action]; // Borrow the transition probabilities
    let next_state = if prob.sample(&mut rng) < transition[0] { 0 } else { 1 };
    let reward = mdp.rewards[state][action];

    println!(
        "Starting state: {}, Action: {}, Next state: {}, Reward: {}",
        mdp.states[state], mdp.actions[action], mdp.states[next_state], reward
    );
}

This implementation provides a concrete example of decision-making in an MDP. The defined transitions and rewards reflect the probabilistic and reward-driven nature of RL, where agents must navigate uncertainty to maximize cumulative returns.

By integrating theoretical insights and practical coding, this section establishes a strong foundation for understanding and implementing stochastic processes and MDPs in Rust, setting the stage for advanced RL algorithms.

2.2. Linear Algebra and Matrix Operations in RL link

Linear algebra is a cornerstone of reinforcement learning (RL), as it provides a structured way to handle the multidimensional nature of the problems RL seeks to solve. At its core, RL deals with understanding and optimizing the behavior of agents within environments characterized by states, actions, rewards, and transitions. Linear algebra enables the representation of these components using vectors and matrices, offering a compact and efficient way to model complex relationships. For instance, transition probabilities, which describe the likelihood of moving from one state to another given an action, are naturally represented as matrices. Reward functions, often multi-dimensional and tied to different state-action pairs, can be encoded as vectors. Through linear algebraic operations, such as matrix multiplication and inversion, RL algorithms can compute policies and value functions, unlocking the ability to optimize agent performance in environments with potentially high complexity.

Figure 2: Use cases of linear algebra in RL models.

Moreover, understanding linear algebra is critical for implementing modern RL techniques that rely heavily on matrix computations. For example, value iteration and policy evaluation involve solving systems of linear equations, which require a solid grasp of matrix transformations and decompositions. Techniques such as singular value decomposition (SVD) and eigenvalue analysis are essential in advanced RL scenarios where dimensionality reduction or stability analysis is needed. Even more fundamentally, the connection between linear algebra and neural networks—a backbone of deep reinforcement learning—is undeniable, as neural network weights and activations are expressed and computed through matrix operations. A robust understanding of linear algebra empowers practitioners to navigate these mathematical tools, enhancing their ability to design, debug, and optimize RL systems effectively.

Linear algebra provides the tools to model and solve problems involving multidimensional data structures such as state-action spaces, transition probabilities, and reward functions. At its heart are vectors and matrices, which are the building blocks for representing RL dynamics. A vector, denoted $\mathbf{v}$, is a one-dimensional array of scalars that often represents quantities like state values or policy probabilities:

$$ \mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}. $$

Matrices extend this concept to two-dimensional arrays, with each entry representing a specific relationship between two entities. A matrix $\mathbf{M}$ of size $m \times n$ can be written as:

$$ \mathbf{M} = \begin{bmatrix} m_{11} & m_{12} & \cdots & m_{1n} \\ m_{21} & m_{22} & \cdots & m_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ m_{m1} & m_{m2} & \cdots & m_{mn} \end{bmatrix}. $$

Matrix operations, such as addition, multiplication, and inversion, are essential for RL computations. For example, the matrix product $\mathbf{C} = \mathbf{A} \cdot \mathbf{B}$, where $\mathbf{A}$ is an $m \times n$ matrix and $\mathbf{B}$ is an $n \times p$ matrix, is defined as:

$$ c_{ij} = \sum_{k=1}^n a_{ik} b_{kj}. $$

In RL, these operations form the basis for calculating state values, optimizing policies, and modeling transitions in Markov Decision Processes (MDPs).

Matrix operations are indispensable in RL, particularly when solving systems of linear equations that arise during value iteration and policy evaluation. These operations allow for compact and efficient representations of the underlying computations.

Consider the Bellman equation, which describes the value function $\mathbf{v}$ of an MDP:

$$ \mathbf{v} = \mathbf{R} + \gamma \mathbf{P} \mathbf{v}, $$

where:

• $\mathbf{v}$: Vector of state values.

• $\mathbf{R}$: Reward vector.

• $\mathbf{P}$: State transition matrix.

• $\gamma$: Discount factor.

Rearranging gives a system of linear equations:

$$ (\mathbf{I} - \gamma \mathbf{P}) \mathbf{v} = \mathbf{R}. $$

Here, $\mathbf{I}$ is the identity matrix. The matrix $(\mathbf{I} - \gamma \mathbf{P})$ encapsulates the interaction between states and their future rewards, while solving this system yields the optimal value function.

Another application is in policy evaluation, where we iteratively refine the value estimates of a given policy by solving similar equations. These computations, heavily reliant on matrix operations, highlight the centrality of linear algebra in RL.

The concepts of eigenvalues and eigenvectors are crucial for understanding the stability and dynamics of RL models, particularly those involving Markov chains and iterative algorithms. For a square matrix $\mathbf{A}$, an eigenvector $\mathbf{x}$ and its corresponding eigenvalue $\lambda$ satisfy the relationship:

$$ \mathbf{A} \mathbf{x} = \lambda \mathbf{x}. $$

The eigenvalue $\lambda$ describes the magnitude by which the eigenvector $\mathbf{x}$ is scaled under the transformation defined by $\mathbf{A}$.

In RL, eigenvalues and eigenvectors provide insight into the convergence of iterative algorithms. For example, the spectral radius (largest absolute eigenvalue) of the matrix $\gamma \mathbf{P}$ determines whether the solution to $(\mathbf{I} - \gamma \mathbf{P}) \mathbf{v} = \mathbf{R}$ converges. If the spectral radius is less than 1, the system is stable, ensuring the iterative computation of $\mathbf{v}$ will converge to the correct values.

Spectral analysis is also key to understanding the long-term behavior of Markov chains. The stationary distribution of a Markov chain corresponds to the eigenvector of its transition matrix $\mathbf{P}$ associated with the eigenvalue $\lambda = 1$. This stationary distribution reveals the probabilities of being in each state after a large number of transitions.

Matrix decomposition methods, such as LU decomposition and Singular Value Decomposition (SVD), simplify complex RL computations. LU decomposition factors a matrix $\mathbf{A}$ into:

$$\mathbf{A} = \mathbf{L} \mathbf{U},$$

where $\mathbf{L}$ is a lower triangular matrix and $\mathbf{U}$ is an upper triangular matrix. This decomposition is particularly useful when solving linear systems repeatedly, as it avoids redundant computations.

Similarly, SVD decomposes a matrix $\mathbf{A}$ into three components:

$$ \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top, $$

where $\mathbf{U}$ and $\mathbf{V}$ are orthogonal matrices, and $\mathbf{\Sigma}$ is a diagonal matrix of singular values. SVD is powerful for dimensionality reduction and stability analysis in RL, where large-scale problems require computational efficiency.

The following examples demonstrate linear algebra operations in Rust using ndarray and nalgebra. The first example covers basic matrix operations like addition and multiplication, essential for implementing Bellman updates. Next, we solve a system of linear equations using $(\mathbf{I} - \gamma \mathbf{P}) \mathbf{v} = \mathbf{R}$, illustrating its role in computing value functions. Finally, we compute eigenvalues and eigenvectors to analyze the stability and long-term behavior of RL models.

The first implementation demonstrates how to create and manipulate matrices using the ndarray crate. Operations like addition and multiplication are directly mapped to RL tasks like value updates.

[dependencies]
ndarray = "0.16.1"

use ndarray::Array2;

fn main() {
    // Define two matrices
    let a = Array2::from_shape_vec((2, 2), vec![1.0, 2.0, 3.0, 4.0]).unwrap();
    let b = Array2::from_shape_vec((2, 2), vec![5.0, 6.0, 7.0, 8.0]).unwrap();

    // Perform matrix addition
    let c = &a + &b;
    println!("Matrix addition:\n{}", c);

    // Perform matrix multiplication
    let d = a.dot(&b);
    println!("Matrix multiplication:\n{}", d);
}

This code shows how matrices represent the interactions between states and transitions, where addition combines effects and multiplication propagates state probabilities.

Next, we solve $(\mathbf{I} - \gamma \mathbf{P}) \mathbf{v} = \mathbf{R}$ to compute the value function, an essential task in RL.

[dependencies]
nalgebra = "0.33.2"

use nalgebra::{Matrix2, Vector2};

fn main() {
    let gamma = 0.9; // Discount factor
    let p = Matrix2::new(0.7, 0.3, 0.4, 0.6); // Transition matrix
    let r = Vector2::new(5.0, 10.0); // Reward vector

    let identity: Matrix2<f64> = Matrix2::identity(); // Explicit type for identity matrix
    let lhs: Matrix2<f64> = identity - gamma * p; // Compute (I - gamma * P)
    let v = lhs.lu().solve(&r).unwrap(); // Solve for v

    println!("Value function:\n{}", v);
}

This demonstrates the power of linear algebra for solving RL problems efficiently and accurately.

Finally, we compute eigenvalues and eigenvectors to analyze Markov chains' stability.

use nalgebra::DMatrix;

fn main() {
    let p = DMatrix::from_row_slice(3, 3, &[
        0.5, 0.2, 0.3,
        0.3, 0.4, 0.3,
        0.2, 0.4, 0.4,
    ]);

    let eigen = p.symmetric_eigen();
    println!("Eigenvalues:\n{}", eigen.eigenvalues);
    println!("Eigenvectors:\n{}", eigen.eigenvectors);
}

This example highlights how eigenvalues reveal convergence and eigenvectors identify stationary distributions, connecting theory to practical RL analysis.

By blending theoretical foundations with hands-on Rust implementations, this section equips readers to understand and apply linear algebra in RL, enabling efficient computation and robust problem-solving.

2.3. Dynamic Programming and Bellman Equations link

Dynamic Programming (DP) is a cornerstone of computational problem-solving, particularly in scenarios where problems exhibit overlapping subproblems and optimal substructure properties. At its essence, DP transforms complex, seemingly intractable problems into a series of smaller, manageable subproblems, solving each one only once and storing their solutions in a systematic way. This approach eliminates the inefficiency of redundant computations, enabling solutions to be built up from the ground floor efficiently. Think of DP as building a staircase: instead of jumping to the top in one go or calculating each step anew every time, DP ensures that you solve for each step once, storing the result to reuse it as you ascend further. This systematic reuse of prior results makes DP a highly efficient strategy, particularly in reinforcement learning (RL), where decisions must be made sequentially in environments with numerous states and possible actions.

Figure 3: The role of dynamic programming in Reinforcement Learning to find optimal solutions of complex problems.

To illustrate DP with a relatable analogy, imagine you're planning a road trip across a series of cities. Without DP, you might repeatedly calculate the best route from your starting city to every destination. This is like solving the same puzzle over and over, wasting time and resources. DP, on the other hand, allows you to calculate and store the best route from each city to your final destination just once. This stored knowledge lets you quickly determine the optimal route no matter where you start. In the context of RL, the Bellman equation, a cornerstone of DP, plays a similar role. It formalizes the relationship between a state, its possible actions, and their expected outcomes, allowing an agent to learn the value of each state based on its future rewards. By storing these computed values, the Bellman equation ensures that the agent doesn't need to repeatedly recalculate the same outcomes, streamlining its learning process in a dynamic environment. This combination of efficiency and systematic reuse is why DP and the Bellman equation are integral to solving sequential decision-making problems in RL.

Mathematically, DP relies on recursive relationships. Suppose the solution to a problem V(s)V(s)V(s) depends on smaller components $V(s')$. Then $V(s)$ can be expressed as:

$$ V(s) = \text{immediate cost at } s + \text{best future cost reachable from } s. $$

In RL, this recursion plays out in the Bellman equations, where the value of a state is the reward received plus the expected value of future states.

The Bellman equations are the cornerstone of RL, defining the recursive relationships between the value of a state and its successor states. They come in two flavors: the Bellman expectation equation for evaluating a fixed policy and the Bellman optimality equation for finding the best possible policy.

The Bellman expectation equation captures the idea that the value of a state under a policy $\pi$, $V^\pi(s)$, is the immediate reward plus the discounted expected value of successor states:

$$ V^\pi(s) = \mathbb{E}_\pi \left[ R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^\pi(s') \right]. $$

Here’s an analogy: imagine climbing stairs where each step has a reward. If you follow a fixed strategy (policy), the value of your current step is the reward from this step plus the discounted value of all future steps.

The Bellman optimality equation generalizes this to optimal decision-making:

$$ V^*(s) = \max_a \left[ R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^*(s') \right]. $$

This equation says the value of a state is the best possible outcome achievable by choosing the optimal action. Using the stair analogy, instead of following a fixed strategy, you now choose the step with the maximum reward and the best future steps ahead.

These equations are iteratively solved in RL algorithms to compute either the optimal value function $V^*(s)$ or the value function under a given policy $V^\pi(s)$.

Dynamic programming ensures computational efficiency using memoization or lookup tables. A lookup table stores solutions to subproblems, enabling instant retrieval. In RL, this translates into maintaining tables like the value table $V(s)$, which stores the value of each state, or the Q-table $Q(s, a)$, which stores the value of taking an action in a given state.

Think of memoization like a library catalog. Instead of recalculating the answer every time you need information, the catalog helps you quickly retrieve stored knowledge. Similarly, DP avoids recomputing subproblem solutions, making it scalable and efficient for RL tasks.

The recursive structure of the Bellman equations arises from the Markov property, which asserts that the future depends only on the current state and action, not the past. This property allows RL algorithms to iteratively update value estimates. For example, in value iteration, the Bellman equation serves as the update rule:

$$ V(s) \leftarrow \max_a \left[ R(s, a) + \gamma \sum_{s'} P(s'|s, a) V(s') \right]. $$

An analogy for recursion is solving a jigsaw puzzle. Instead of focusing on the whole puzzle at once, you complete smaller sections and fit them together. The Bellman equations recursively solve RL problems in smaller pieces, iteratively building up to the optimal solution.

The following code demonstrates how to implement value iteration and policy iteration, two key dynamic programming techniques in RL, using Rust. In the first example, we compute the optimal value function for a simple RL environment using the Bellman optimality equation. In the second example, we combine policy evaluation and improvement to refine a policy iteratively until convergence. The implementations use Rust’s safety and performance features to illustrate the power of DP techniques.

In this example, we define a simple MDP with three states and two actions. Using the Bellman optimality equation, we iteratively compute the value function for each state.

use ndarray::Array2;

fn main() {
    let states = 3; // Number of states
    let actions = 2; // Number of actions
    let gamma = 0.9; // Discount factor

    // Transition probabilities: P(s' | s, a)
    let transitions = vec![
        vec![
            Array2::from_shape_vec((3, 3), vec![0.7, 0.2, 0.1, 0.1, 0.6, 0.3, 0.0, 0.1, 0.9]).unwrap(),
            Array2::from_shape_vec((3, 3), vec![0.5, 0.4, 0.1, 0.0, 0.8, 0.2, 0.2, 0.3, 0.5]).unwrap(),
        ],
    ];

    // Rewards: R(s, a)
    let rewards = Array2::from_shape_vec((3, 2), vec![5.0, 10.0, 0.0, 3.0, -1.0, 2.0]).unwrap();

    // Initialize value function
    let mut values = vec![0.0; states];
    let mut new_values = values.clone();

    // Value iteration loop
    for _ in 0..100 {
        for s in 0..states {
            let mut max_value = f64::NEG_INFINITY;
            for a in 0..actions {
                let mut value = rewards[(s, a)];
                for s_next in 0..states {
                    value += gamma * transitions[0][a][[s, s_next]] * values[s_next];
                }
                max_value = max_value.max(value);
            }
            new_values[s] = max_value;
        }
        values.clone_from(&new_values);
    }

    println!("Optimal value function: {:?}", values);
}

This implementation demonstrates the iterative computation of the value function using value iteration. The core logic involves calculating the maximum expected value over all possible actions for each state, incorporating immediate rewards and future discounted values. The transitions are stored as matrices, and the rewards are encoded as a table for efficiency. Iterative updates to the value function continue until convergence, resulting in the optimal value function.

The next example implements policy iteration, which alternates between evaluating a policy and improving it until the optimal policy is reached.

use ndarray::{Array2, Array1};

fn main() {
    let states = 3;
    let actions = 2;
    let gamma = 0.9;

    // Define the reward matrix
    let rewards = Array2::from_shape_vec((states, actions), vec![
        5.0, 10.0,  // Rewards for state 0
        3.0, 8.0,   // Rewards for state 1
        2.0, 4.0,   // Rewards for state 2
    ]).unwrap();

    // Define the transition probabilities as a vector of 2D arrays
    let transitions = vec![
        Array2::from_shape_vec((states, states), vec![
            0.7, 0.3, 0.0,  // Transition probabilities for action 0
            0.4, 0.6, 0.0,
            0.0, 0.0, 1.0,
        ]).unwrap(),
        Array2::from_shape_vec((states, states), vec![
            0.5, 0.5, 0.0,  // Transition probabilities for action 1
            0.3, 0.7, 0.0,
            0.0, 0.0, 1.0,
        ]).unwrap(),
    ];

    // Initialize policy
    let mut policy = Array1::from_elem(states, 0);

    // Policy iteration loop
    loop {
        // Policy evaluation
        let mut values = Array1::zeros(states);
        for _ in 0..100 {
            for s in 0..states {
                let a = policy[s];
                values[s] = rewards[(s, a)]
                    + gamma * (0..states)
                        .map(|s_next| transitions[a][[s, s_next]] * values[s_next])
                        .sum::<f64>();
            }
        }

        // Policy improvement
        let mut policy_stable = true;
        for s in 0..states {
            let mut best_action = 0;
            let mut best_value = f64::NEG_INFINITY;
            for a in 0..actions {
                let value = rewards[(s, a)]
                    + gamma * (0..states)
                        .map(|s_next| transitions[a][[s, s_next]] * values[s_next])
                        .sum::<f64>();
                if value > best_value {
                    best_value = value;
                    best_action = a;
                }
            }

            if policy[s] != best_action {
                policy[s] = best_action;
                policy_stable = false;
            }
        }

        if policy_stable {
            break;
        }
    }

    println!("Optimal policy: {:?}", policy);
}

Policy iteration alternates between two phases: evaluating the current policy to determine its value function and improving the policy by selecting actions that maximize expected rewards. The implementation uses the Bellman expectation equation during policy evaluation and updates the policy greedily based on improved value estimates. The loop terminates when the policy stabilizes, ensuring convergence to the optimal policy.

These examples showcase the power and elegance of dynamic programming techniques in RL, bridging mathematical principles with efficient Rust implementations to solve complex decision-making problems.

2.4. Optimization Techniques in RL link

Optimization is a foundational pillar in reinforcement learning (RL), enabling agents to learn and adapt effectively in complex and dynamic environments. At its core, RL aims to solve sequential decision-making problems where an agent interacts with its environment to achieve a long-term objective. Optimization plays a critical role in this process by fine-tuning the agent's behavior to maximize cumulative rewards. Without robust optimization techniques, RL would be reduced to mere trial-and-error processes, making it infeasible to tackle large-scale or high-dimensional problems like robotics, game playing, or autonomous systems.

The importance of optimization in RL stems from its ability to address two key challenges: exploration and exploitation. Exploration involves discovering new strategies or actions that might yield higher rewards, while exploitation focuses on leveraging known information to achieve the best outcomes. Balancing these aspects requires optimization to handle complex trade-offs efficiently. For instance, in stochastic environments where outcomes are uncertain, optimization helps an agent estimate expected rewards and refine its policies systematically. This ensures that learning converges to an optimal or near-optimal strategy, even when faced with noisy or incomplete data.

Figure 4: The optimization is important aspect of RL system.

The scope of optimization in RL is vast, encompassing tasks like value function approximation, policy optimization, and gradient-based learning. Techniques such as stochastic gradient descent (SGD), Q-learning, and actor-critic methods are all rooted in optimization principles. Beyond algorithmic development, optimization also addresses practical concerns like computational efficiency and scalability. For example, modern advancements like proximal policy optimization (PPO) and trust region policy optimization (TRPO) are designed to improve stability and performance in high-dimensional spaces. In essence, optimization serves as the mathematical backbone that empowers RL to navigate and solve real-world challenges effectively, from managing resource allocation to controlling self-driving vehicles.

Optimization is the engine driving learning in reinforcement learning (RL). At its heart is the goal of adjusting parameters to minimize or maximize a target function iteratively. A cornerstone concept in optimization is the gradient, which provides the direction of the steepest ascent or descent. Imagine hiking up a hill in thick fog; the gradient tells you which direction leads upward or downward most steeply. Mathematically, the gradient of a scalar function $f(\mathbf{w})$ with respect to a parameter vector $\mathbf{w}$ is:

$$ \nabla f(\mathbf{w}) = \begin{bmatrix} \frac{\partial f}{\partial w_1} \\ \frac{\partial f}{\partial w_2} \\ \vdots \\ \frac{\partial f}{\partial w_n} \end{bmatrix}. $$

The gradient descent algorithm uses this information to iteratively update parameters w\\mathbf{w}w in the direction opposite to the gradient (to minimize the function):

$$ \mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla f(\mathbf{w}_t), $$

where $\eta$, the learning rate, controls the size of each step. Think of the learning rate as your hiking speed; too fast, and you might overshoot the destination; too slow, and progress becomes painstakingly gradual.

In RL, optimization is used to improve policies and value functions. For instance, in policy optimization, the goal is to maximize the expected return:

$$ J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_{t=0}^\infty \gamma^t R(s_t, a_t) \right], $$

where $\pi_\theta$ is the policy parameterized by $\theta$, $\tau$ represents trajectories, and $\gamma$ is the discount factor.

Optimization techniques like stochastic gradient descent (SGD) and its variants are particularly suited for RL due to the high-dimensional and stochastic nature of RL problems. The policy gradient theorem provides a foundation for gradient-based methods:

$$ \nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \nabla_\theta \log \pi_\theta(a_t | s_t) Q^\pi(s_t, a_t) \right], $$

where $Q^\pi(s_t, a_t)$ represents the expected return of taking action $a_t$ in state $s_t$. Imagine you're running a restaurant and want to allocate resources to dishes that sell well. The policy gradient theorem essentially tells you to focus on actions (dishes) that perform best, adjusting the policy (menu) accordingly.

Optimization in RL often leverages stochasticity to handle uncertainty, making it possible to update policies based on noisy feedback from the environment. This contrasts with traditional gradient descent, which requires a complete dataset to compute precise gradients. The stochastic approach updates parameters using estimates based on subsets (mini-batches) of data:

$$ \mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla \tilde{f}(\mathbf{w}_t), $$

where $\nabla \tilde{f}$ is the gradient estimate. Variants like momentum and Adam further enhance optimization by accelerating convergence and improving stability.

Optimization in RL must carefully manage the trade-off between exploration (trying new actions to discover better strategies) and exploitation (choosing actions that maximize immediate rewards). Imagine running a coffee shop: you could either stick to tried-and-true recipes (exploitation) or experiment with new drinks to potentially attract more customers (exploration). Optimization algorithms strike this balance by gradually shifting focus toward exploitation as learning progresses.

The learning rate $\eta$ significantly impacts this balance. A large $\eta$ encourages rapid exploration but risks instability, like driving a car with jerky accelerations. A small $\eta$, on the other hand, ensures steady but slow progress, akin to walking carefully to avoid tripping.

Optimization in RL shares many principles with other areas of machine learning, such as supervised learning. In supervised learning, the objective is to minimize a predefined loss function, such as the mean squared error. Similarly, in RL, optimization minimizes the negative expected return or improves policy performance. However, RL introduces additional complexity due to delayed rewards and the stochastic nature of environment feedback.

For example, in supervised learning, gradients are computed directly from labeled data. In RL, gradients often rely on estimates derived from sampled trajectories, requiring careful handling of variance to maintain stability.

The following Rust implementations demonstrate optimization techniques in RL. The first example uses gradient descent to minimize a simple quadratic loss function, showcasing basic optimization dynamics. The second example implements a policy gradient method, allowing exploration of different learning rates and convergence criteria. Finally, the third example compares the performance of advanced optimization techniques like SGD, momentum, and Adam in a simple RL task.

This code demonstrates gradient descent to minimize a quadratic function, $f(w) = (w - 3)^2$, with its minimum at $w = 3$.

fn main() {
    // Define a simple quadratic function: f(w) = (w - 3)^2
    let gradient = |w: f64| 2.0 * (w - 3.0);

    // Initialize parameters
    let mut w = 0.0; // Initial guess
    let learning_rate = 0.1;

    // Gradient descent loop
    for _ in 0..100 {
        let grad = gradient(w);
        w -= learning_rate * grad; // Update w using gradient descent
    }

    println!("Optimized parameter: {}", w);
}

The function $f(w) = (w - 3)^2$ represents a simple optimization problem. Starting with an initial guess, gradient descent iteratively updates www by subtracting the gradient scaled by the learning rate. Each iteration brings www closer to the optimal solution $w = 3$. This process mirrors how RL policies are optimized using gradients.

This code demonstrates a simple policy gradient algorithm, optimizing a stochastic policy to maximize rewards.

use rand::Rng;

fn main() {
    // Define a simple stochastic policy: π(a|s) = θ
    let mut theta = 0.5; // Policy parameter
    let learning_rate = 0.1;

    // Simulated environment feedback: Reward function R(s, a)
    let reward = |a: f64| if a > 0.5 { 1.0 } else { 0.0 };

    // Policy gradient loop
    for _ in 0..100 {
        let action = rand::thread_rng().gen_range(0.0..1.0); // Sample action
        let grad = (action - theta) * reward(action); // Policy gradient
        theta += learning_rate * grad; // Update policy parameter
    }

    println!("Optimized policy parameter: {}", theta);
}

In this example, the policy is represented by a parameter $\theta$, determining the probability of taking actions. The policy gradient update adjusts $\theta$ to increase the likelihood of actions yielding higher rewards. The reward function simulates an environment where actions greater than 0.5 are favorable. This algorithm showcases the essence of policy gradient methods in RL.

This code demonstrates the implementation of various optimization algorithms commonly used in machine learning and reinforcement learning to update model parameters effectively. The optimization methods include Stochastic Gradient Descent (SGD), Momentum, AdaGrad, RMSProp, and Adam, each addressing different challenges in learning. These methods iteratively adjust a parameter w based on gradients computed from an example objective function, illustrating their mechanics and how they influence convergence. The code provides a comparative view of how each algorithm accumulates information about the gradient (e.g., through momentum or adaptive learning rates) to optimize the parameter's update path, ultimately converging to the optimal value. It highlights the differences in their update strategies and is a practical demonstration of foundational optimization concepts in machine learning.

fn sgd_update(w: &mut f64, grad: f64, lr: f64) {
    *w -= lr * grad; // Standard gradient descent
}

fn momentum_update(w: &mut f64, grad: f64, lr: f64, momentum: &mut f64, beta: f64) {
    *momentum = beta * *momentum + grad; // Add momentum
    *w -= lr * *momentum;
}

fn adam_update(w: &mut f64, grad: f64, lr: f64, m: &mut f64, v: &mut f64, t: usize, beta1: f64, beta2: f64, eps: f64) {
    *m = beta1 * *m + (1.0 - beta1) * grad;
    *v = beta2 * *v + (1.0 - beta2) * grad * grad;
    let m_hat = *m / (1.0 - beta1.powi(t as i32));
    let v_hat = *v / (1.0 - beta2.powi(t as i32));
    *w -= lr * m_hat / (v_hat.sqrt() + eps);
}

fn adagrad_update(w: &mut f64, grad: f64, lr: f64, cache: &mut f64, eps: f64) {
    *cache += grad * grad; // Accumulate squared gradients
    *w -= lr * grad / (cache.sqrt() + eps); // Adjust learning rate for each parameter
}

fn rmsprop_update(w: &mut f64, grad: f64, lr: f64, cache: &mut f64, beta: f64, eps: f64) {
    *cache = beta * *cache + (1.0 - beta) * grad * grad; // Exponentially weighted average of squared gradients
    *w -= lr * grad / (cache.sqrt() + eps); // Adjust learning rate based on moving average
}

fn main() {
    let gradient = |w: f64| 2.0 * (w - 3.0);

    // SGD
    let mut w = 0.0;
    for _ in 0..100 {
        let grad = gradient(w); // Compute gradient first
        sgd_update(&mut w, grad, 0.1);
    }
    println!("SGD result: {}", w);

    // Momentum
    w = 0.0;
    let mut momentum = 0.0;
    for _ in 0..100 {
        let grad = gradient(w);
        momentum_update(&mut w, grad, 0.1, &mut momentum, 0.9);
    }
    println!("Momentum result: {}", w);

    // Adam
    w = 0.0;
    let mut m = 0.0;
    let mut v = 0.0;
    for t in 1..=100 {
        let grad = gradient(w);
        adam_update(&mut w, grad, 0.1, &mut m, &mut v, t, 0.9, 0.999, 1e-8);
    }
    println!("Adam result: {}", w);

    // AdaGrad
    w = 0.0;
    let mut cache_adagrad = 0.0;
    for _ in 0..100 {
        let grad = gradient(w);
        adagrad_update(&mut w, grad, 0.1, &mut cache_adagrad, 1e-8);
    }
    println!("AdaGrad result: {}", w);

    // RMSProp
    w = 0.0;
    let mut cache_rmsprop = 0.0;
    for _ in 0..100 {
        let grad = gradient(w);
        rmsprop_update(&mut w, grad, 0.1, &mut cache_rmsprop, 0.9, 1e-8);
    }
    println!("RMSProp result: {}", w);
}

The code implements and compares five popular optimization algorithms: Stochastic Gradient Descent (SGD), Momentum, AdaGrad, RMSProp, and Adam, by applying them to iteratively optimize a single parameter, w. Each algorithm updates w based on the gradient of an example objective function, $f(w) = (w - 3)^2$, where the gradient is calculated as $2(w - 3)$. SGD performs simple gradient updates, while Momentum incorporates a velocity term to accelerate convergence. AdaGrad adjusts the learning rate for each update by scaling it inversely with the square root of accumulated squared gradients, adapting to steep or flat regions. RMSProp modifies AdaGrad by decaying past gradients to focus on recent updates. Adam combines Momentum and RMSProp, maintaining moving averages of gradients and their squared values for robust updates. The main function sequentially applies each algorithm to demonstrate their individual behaviors and how they converge toward the optimal value of w = 3.

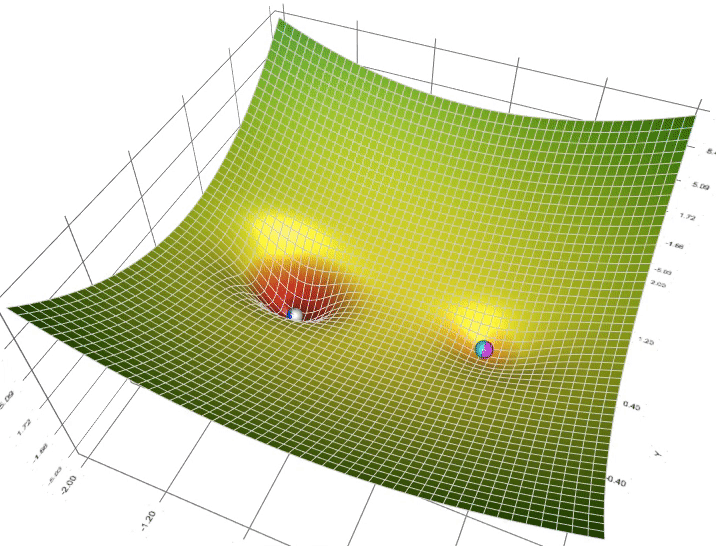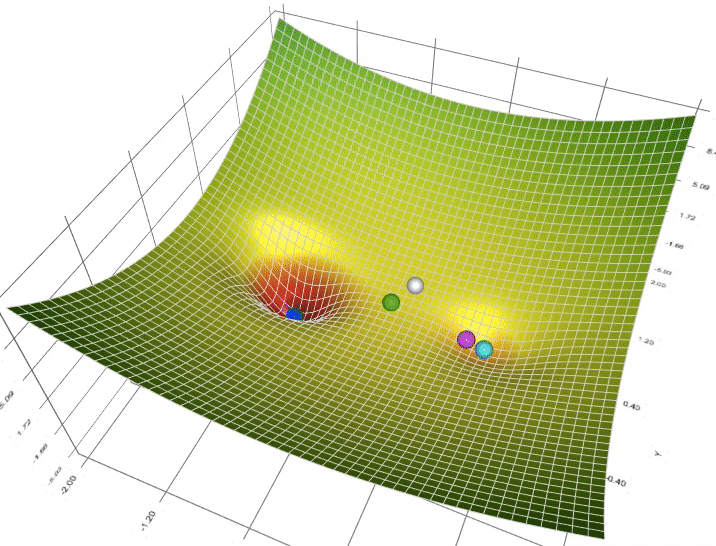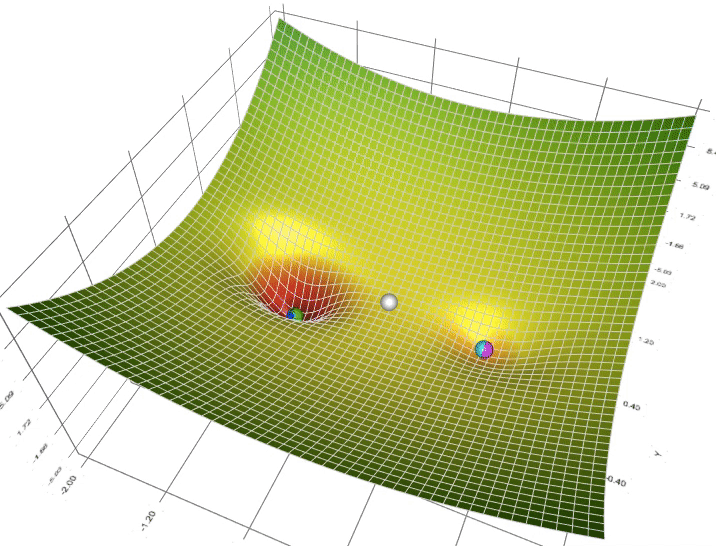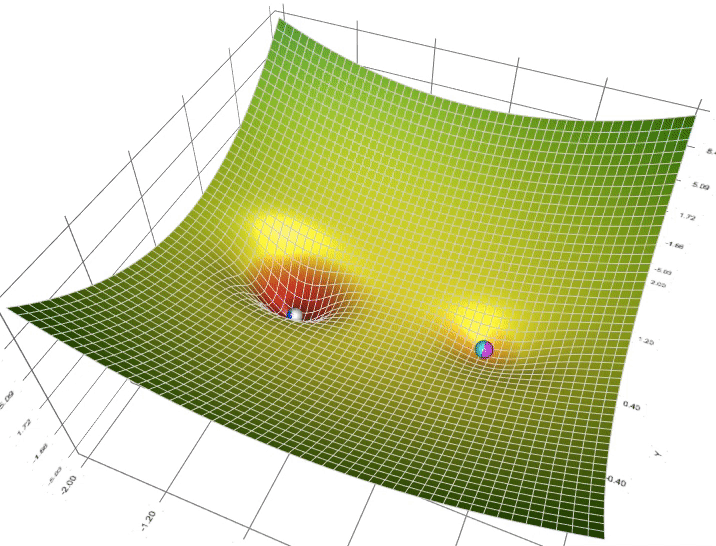
Figure 5: Animation of 5 gradient descent methods on a surface: SGD (cyan), momentum (magenta), AdaGrad (white), RMSProp (green), Adam (blue). Left well is the global minimum; right well is a local minimum. (Credit: Lili Jiang)

In practice of optimization, Stochastic Gradient Descent (SGD), Momentum, AdaGrad, RMSProp, and Adam represent a progression of increasingly advanced strategies for efficiently navigating complex optimization landscapes in machine learning and reinforcement learning. These methods address the fundamental problem of finding the minimum (or maximum) of a target function by iteratively updating parameters based on gradients. Each method improves upon its predecessor, introducing innovations to overcome challenges such as oscillations, slow convergence, and uneven or sparse gradients.

SGD, the simplest of these methods, updates parameters in the direction of the negative gradient, akin to taking steps downhill in the steepest direction. It is computationally efficient and forms the backbone of most optimization techniques. However, SGD's simplicity can be a drawback in real-world scenarios with noisy or uneven gradients, as it often results in zigzagging and slow progress, particularly in areas where gradients are small or flat. For example, in optimization landscapes with long, narrow valleys, SGD requires numerous small adjustments, significantly increasing computation time and reducing efficiency.

Momentum addresses these issues by introducing a "velocity" term, which accumulates the influence of past gradients to smooth the optimization path. Imagine rolling a heavy ball down a hill—the ball builds momentum as it moves in the same direction, helping it traverse shallow gradients faster and ignore small oscillations caused by uneven terrain. This method accelerates convergence, especially in deep valleys, by allowing optimization steps to build inertia, but it may lag when encountering sharp changes in direction, as the accumulated velocity takes time to adjust.

AdaGrad introduces adaptivity to the learning rate, making it particularly effective in scenarios where some parameters require larger updates than others. It adjusts the step size for each parameter based on the cumulative sum of past squared gradients. This approach is akin to hiking while keeping track of how rugged each direction has been. On steep paths, AdaGrad takes smaller, more cautious steps, while on flatter paths, it moves more boldly. This makes it especially powerful in handling sparse data or problems with non-uniform gradients. However, AdaGrad's reliance on cumulative gradients often causes it to slow down excessively over time, as the learning rate becomes overly small.

RMSProp refines AdaGrad by introducing an exponential decay term, which selectively "forgets" older gradients to maintain a balance between past and recent information. Imagine hiking with a memory elastic band that stretches to track recent terrain but gradually releases older, less relevant information. By smoothing the gradient accumulation over time, RMSProp ensures that optimization remains adaptive without being overly influenced by historical gradients. This makes it highly effective for non-stationary problems, such as deep reinforcement learning, where the optimization landscape changes dynamically as the agent learns.

Adam (Adaptive Moment Estimation) integrates the advantages of Momentum and RMSProp into a single, powerful optimizer. It combines the smooth progress of Momentum with the adaptive learning rate adjustments of RMSProp. Picture hiking with both a guide who remembers past directions (Momentum) and a dynamically updating map that adjusts step sizes based on the steepness of the terrain (RMSProp). Adam maintains two moving averages: one for the gradients (Momentum) and another for the squared gradients (RMSProp), correcting both for bias in the early stages of training. This dual adaptation makes Adam highly effective in diverse scenarios, from convex optimization problems to non-convex landscapes with plateaus, sharp cliffs, and saddle points. Its robustness and ability to perform well with minimal hyperparameter tuning have made Adam the default choice for many deep learning applications.

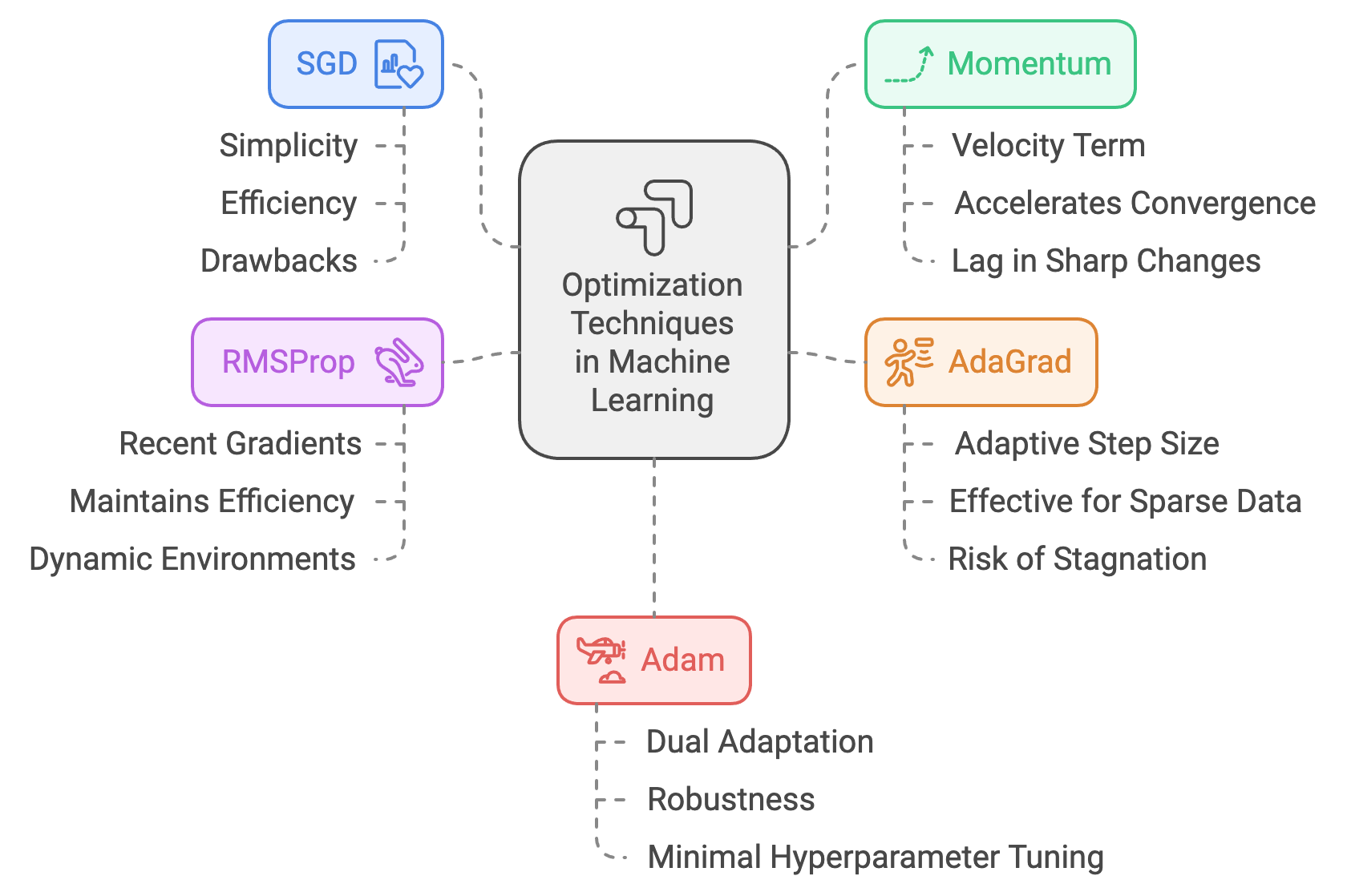
Figure 6: Common optimizers for Machine Learning.

In summary, these optimization techniques represent an evolution in addressing the challenges of modern machine learning. SGD offers simplicity but struggles with inefficiencies in complex landscapes. Momentum accelerates progress by leveraging the inertia of past gradients, while AdaGrad adapts step sizes to handle sparse or uneven data but risks stagnation. RMSProp improves upon AdaGrad by focusing on recent gradients, maintaining efficiency in dynamic environments. Adam synthesizes these innovations into a highly adaptive and robust optimizer, balancing speed, stability, and generalization, making it indispensable in solving the diverse and complex problems encountered in machine learning today.

2.5. Conclusion link

Chapter 2 equips you with the mathematical tools necessary to understand and implement reinforcement learning algorithms. By mastering these foundational concepts, you will be able to develop more sophisticated and effective RL systems, leveraging the precision and efficiency of Rust to bring your ideas to life.

2.5.1. Further Learning with GenAI link

Each prompt is crafted to guide you through complex concepts, technical challenges, and practical implementations in Rust, enabling you to develop a robust understanding of how these mathematical principles are applied in modern RL.

• Analyze the role of probability theory in reinforcement learning. How do concepts like random variables, probability distributions, and expectations contribute to the modeling of RL environments? Discuss how Rust can be used to implement these probabilistic concepts in RL simulations.

• Discuss the significance of stochastic processes, particularly Markov chains and Markov Decision Processes (MDPs), in reinforcement learning. How do these processes model the uncertainty and sequential nature of decision-making in RL? Explore the implementation of Markov chains and MDPs in Rust.

• Examine the concept of conditional probability and its relevance to reinforcement learning. How is conditional probability used to model the likelihood of transitions between states in an RL environment? Implement a simple conditional probability model in Rust to simulate state transitions.

• Explore the mathematical structure of Markov Decision Processes (MDPs). How do states, actions, rewards, and transition probabilities interact within an MDP to define an RL problem? Implement a basic MDP in Rust and analyze its behavior under different policies.

• Discuss the importance of stationary distributions and steady-state behavior in Markov chains. How do these concepts relate to the long-term behavior of reinforcement learning agents? Implement a Markov chain in Rust and calculate its stationary distribution.

• Examine the role of linear algebra in reinforcement learning. How are vectors, matrices, and their operations used to represent and solve RL problems? Discuss how matrix operations can be efficiently implemented in Rust using crates like ndarray and nalgebra.

• Analyze the significance of matrix decomposition techniques, such as LU decomposition and Singular Value Decomposition (SVD), in reinforcement learning. How do these techniques simplify the computation of value functions and policies in RL? Implement matrix decomposition in Rust for an RL problem.

• Discuss the concept of eigenvalues and eigenvectors in the context of reinforcement learning. How do these mathematical constructs help analyze the stability and convergence of RL algorithms? Explore the computation of eigenvalues and eigenvectors in Rust for a Markov chain.

• Examine the principles of dynamic programming in reinforcement learning. How does dynamic programming break down complex RL problems into simpler subproblems? Implement a dynamic programming solution in Rust for a simple RL task, such as grid navigation.

• Discuss the Bellman equations and their significance in reinforcement learning. How do Bellman expectation equations and Bellman optimality equations provide the foundation for value iteration and policy iteration? Implement the Bellman equations in Rust to compute value functions.

• Explore the recursive nature of the Bellman equations in reinforcement learning. How do these equations relate the value of a state to the values of successor states? Implement an iterative computation of the Bellman equations in Rust for a policy evaluation task.

• Analyze the role of discount factors in reinforcement learning. How do different discount factors impact the convergence and stability of value functions in RL? Experiment with various discount factors in a Rust-based RL implementation and observe their effects.

• Discuss the importance of optimization techniques in reinforcement learning, particularly in policy optimization methods. How do concepts like gradients and gradient descent apply to RL? Implement a simple gradient descent algorithm in Rust to optimize an RL policy.

• Examine the trade-offs between exploration and exploitation in policy optimization. How do optimization algorithms in RL manage these trade-offs to achieve efficient learning? Implement a policy gradient method in Rust and experiment with different exploration strategies.

• Explore the role of learning rates, convergence criteria, and regularization in optimizing RL algorithms. How do these factors influence the performance and stability of RL models? Implement and analyze the impact of these factors in a Rust-based RL project.

• Discuss the connection between optimization problems in reinforcement learning and other areas of machine learning, such as supervised learning. How do shared optimization techniques benefit both fields? Implement a comparative study of optimization methods in Rust for RL and supervised learning tasks.

• Examine the concept of stochastic gradient descent (SGD) and its variants, such as momentum and Adam, in the context of reinforcement learning. How do these optimization techniques enhance the efficiency of policy learning? Implement SGD and its variants in Rust and compare their performance in RL tasks.

• Discuss the challenges of solving linear systems in reinforcement learning, particularly in the computation of value functions. How can Rust be used to efficiently solve these systems using matrix operations? Implement a Rust-based solution for solving linear systems in an RL context.

• Explore the application of spectral analysis in reinforcement learning. How does spectral analysis help in understanding the dynamics and stability of RL algorithms? Implement spectral analysis in Rust to evaluate the behavior of an RL agent in a Markov chain.

• Analyze the importance of convergence guarantees in dynamic programming and reinforcement learning. How do these guarantees ensure the correctness and reliability of RL algorithms? Implement a dynamic programming algorithm in Rust and investigate its convergence properties.

By engaging with these robust questions, you will not only solidify your theoretical knowledge but also gain hands-on experience in implementing these concepts using Rust.

2.5.2. Hands On Practices link

Here are five in-depth self-exercises for you to practice, designed to solidify their understanding of the mathematical foundations of reinforcement learning and their implementation using Rust.

Exercise 2.1: Implementing and Analyzing Markov Decision Processes (MDPs) link

Task:

• Implement a Markov Decision Process (MDP) in Rust for a simple decision-making scenario, such as navigating a grid world. Define the states, actions, rewards, and transition probabilities.

• Once implemented, analyze how different policies affect the agent's behavior and the overall performance in terms of accumulated rewards.

Challenge:

• Experiment with various policies and modify the reward structure to observe how these changes impact the MDP's behavior. Consider running simulations to see how the agent adapts over time with different policies.

• Compare the performance of deterministic versus stochastic policies in your MDP implementation.

Exercise 2.2: Solving Linear Systems for Value Functions in RL link

Task:

• Implement a system of linear equations in Rust to solve for the value functions in a small-scale reinforcement learning problem. Use techniques like matrix inversion or iterative methods to find the solution.

• Focus on ensuring that the implementation is efficient and can handle variations in the problem's scale or complexity.

Challenge:

• Apply your implementation to different RL scenarios and evaluate the accuracy and convergence speed of your solutions. Consider testing with different discount factors and state-transition matrices.

• Compare the results from your Rust implementation with theoretical values or solutions obtained from other mathematical tools or libraries.

Exercise 2.3: Dynamic Programming and the Bellman Equation link

Task:

• Implement the Bellman equations in Rust for a given RL environment, such as a grid world or a simple game. Use dynamic programming techniques like value iteration to compute the optimal value function.

• Ensure that your implementation accurately reflects the recursive nature of the Bellman equations and is capable of iterating until convergence.

Challenge:

• Experiment with different discount factors and initial value functions to observe how they influence the convergence process. Visualize the progression of value function updates across iterations.

• Extend your implementation to include policy iteration and compare the effectiveness of value iteration versus policy iteration in finding the optimal policy.

Exercise 2.4: Exploring Optimization Techniques in Policy Learning link

Task:

• Implement a policy gradient method in Rust, applying gradient descent to optimize a simple RL policy. Choose a problem with a continuous action space, such as controlling the angle of a pendulum.

• Focus on the optimization process, experimenting with different learning rates, and exploring how they impact the stability and efficiency of learning.

Challenge:

• Compare the performance of different gradient-based optimization techniques, such as stochastic gradient descent (SGD), momentum, and Adam. Analyze which method provides the best trade-off between convergence speed and stability in your RL environment.

• Test your implementation in environments with varying levels of noise and uncertainty to see how robust your optimization technique is under different conditions.

Exercise 2.5: Implementing and Analyzing Stochastic Gradient Descent (SGD) in RL link

Task:

• Implement stochastic gradient descent (SGD) in Rust to optimize an RL model, such as a simple Q-learning algorithm. Focus on the efficiency of the implementation, especially when dealing with large state-action spaces.

• Analyze how the choice of learning rate and batch size affects the performance and convergence of the RL model.

Challenge:

• Experiment with variations of SGD, such as mini-batch SGD, momentum, and adaptive learning rates. Evaluate their impact on the learning process, particularly in terms of reducing variance and accelerating convergence.

• Apply your implementation to a complex RL task, such as a multi-armed bandit problem, and compare the results with those obtained using other optimization methods.

By implementing these techniques in Rust and experimenting with different scenarios and parameters, you will gain valuable insights into how these foundational principles influence the behavior and performance of RL models.