Chapter 4
Dynamic Programming in Reinforcement Learning
"Dynamic programming is not just an algorithmic tool; it’s a way of thinking about problem-solving that changes how we approach the most complex challenges in reinforcement learning." — Richard Bellman
Chapter 4 of RLVR explores the fundamental principles and practical applications of Dynamic Programming (DP) within the context of reinforcement learning, using Rust as the implementation language. The chapter begins with an introduction to DP, highlighting its significance as a method for solving complex problems by breaking them down into simpler subproblems. This section emphasizes the relevance of DP in reinforcement learning, particularly in key algorithms like value iteration and policy iteration, and introduces the principle of optimality, which is central to constructing optimal solutions. The chapter then delves into the Bellman equations, differentiating between the Bellman expectation equation used in policy evaluation and the Bellman optimality equation used in policy optimization, and explains the importance of convergence in ensuring that these iterative processes yield stable, optimal policies. Practical exercises guide readers through implementing basic DP algorithms in Rust, visualizing convergence, and experimenting with different update rules. The chapter continues with a detailed examination of policy evaluation and improvement, where readers learn to implement and visualize the policy iteration process in Rust, exploring how policies evolve and converge to optimal solutions. This is followed by a comprehensive study of value iteration, where the relationship between value iteration and the Bellman optimality equation is explored, along with the trade-offs between computational cost and accuracy. Practical examples demonstrate value iteration in Rust, comparing it with policy iteration and optimizing the process through experimentation. The chapter concludes with an exploration of asynchronous DP methods, which offer advantages in convergence speed and computational efficiency by updating value functions or policies asynchronously. Readers are guided through implementing these methods in Rust, experimenting with state prioritization, and analyzing the performance benefits of asynchronous updates compared to synchronous methods. Through this chapter, readers will gain a deep understanding of how DP techniques underpin reinforcement learning and acquire hands-on experience in implementing and optimizing these algorithms using Rust.
4.1. Introduction to Dynamic Programming (DP)
Dynamic Programming (DP) is a foundational approach used in computer science and mathematics to tackle problems that involve a series of interconnected decisions or computations. The core idea is to decompose a complex problem into smaller, manageable subproblems, solve each subproblem efficiently, and then combine these solutions to arrive at the overall solution. What makes DP unique is its ability to recognize and exploit patterns in problems where the same subproblems recur. Instead of solving these repeated subproblems from scratch each time, DP ensures efficiency by storing their solutions, which can be reused as needed. This systematic reuse not only reduces computational effort but also guarantees that the solutions to the subproblems are consistent and free of errors caused by recomputation.
The principle of optimal substructure underpins the effectiveness of DP. This principle suggests that the solution to a larger problem can be derived from the optimal solutions of its smaller constituent problems. For example, in a shortest-path problem, the shortest path from a starting point to a destination can be built by combining the shortest paths between intermediate points. This property is key to breaking down complex problems in a logical and structured way. By solving and storing the results of smaller problems, DP essentially builds up to the final solution step by step, ensuring that every component of the solution is optimized. This methodology not only simplifies problem-solving but also makes DP a versatile tool for a wide range of applications, from routing algorithms to resource allocation.
Memoization is the secret sauce that makes DP so efficient in handling overlapping subproblems. In many real-world scenarios, the same problem arises multiple times in slightly different forms. Without memoization, solving each instance independently would be computationally expensive and impractical. By storing the results of previously solved subproblems, DP avoids this redundancy and significantly accelerates the solution process. Memoization transforms what could be an exponential problem into a polynomial-time one in many cases, making DP a go-to strategy for solving problems in fields like robotics, machine learning, economics, and network optimization. Whether it’s planning the most efficient route, calculating the maximum profit, or finding the longest common subsequence in strings, DP’s ability to combine mathematical rigor with computational efficiency makes it indispensable in both theoretical and applied domains.
Dynamic Programming (DP) in reinforcement learning (RL) is a methodical and foundational approach for solving Markov Decision Processes (MDPs) by leveraging the full knowledge of the environment's dynamics, such as transition probabilities and rewards. As illustrated, DP systematically computes the value of each state by considering all possible future paths, ensuring an exhaustive and optimal solution. In contrast, Monte Carlo methods rely on sampling complete episodes of experience to estimate state values, which makes them effective when environment models are unavailable but computationally expensive for long trajectories. Temporal-Difference (TD) learning strikes a balance between these approaches by updating state values incrementally based on observed transitions, enabling real-time learning without requiring complete episodes or full environment knowledge. Unlike Monte Carlo or TD, DP's reliance on a perfect model of the environment can be both its strength and limitation, making it ideal for structured problems while less practical for real-world scenarios where such models are unavailable.
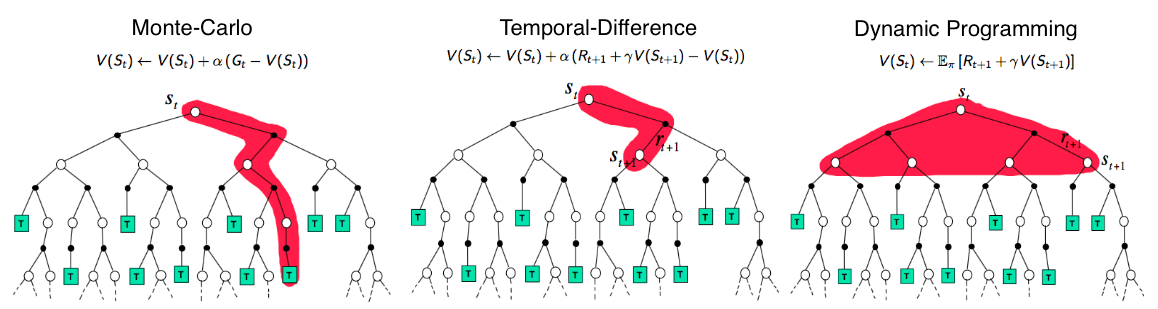
Figure 1: Monte-Carlo, Temporal-Difference and Dynamic Programming methods in RL.
Mathematically, consider a problem with a value function $V(s)$ representing the solution for a state $s$. DP solves this iteratively or recursively by using relationships between $V(s)$ and its subproblems. For example:
$$ V(s) = \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V(s') \right], $$
where:
$R(s, a)$ is the immediate reward for taking action aaa in state $s$,
$\gamma$ is the discount factor,
$P(s' | s, a)$ is the transition probability to state $s'$ after taking action $a$.
DP is particularly relevant in reinforcement learning (RL) as it provides the foundation for solving Markov Decision Processes (MDPs). Core RL algorithms such as value iteration and policy iteration are direct applications of DP principles.
An analogy for DP is planning a trip. To reach your destination optimally (the solution), you break the journey into smaller legs (subproblems). By solving each leg optimally (subproblem solutions), you construct the best overall route (optimal solution).
The principle of optimality, introduced by Richard Bellman, is a cornerstone of DP. It states:
“An optimal policy has the property that, regardless of the initial state and initial decision, the remaining decisions constitute an optimal policy for the subproblem starting from the state resulting from the first decision.”
In practical terms, this means that solving the problem for the entire state space can be reduced to solving it for a single state and propagating its solution to others. This principle underpins the recursive nature of DP algorithms and allows them to decompose problems effectively.
The Bellman equation represents the recursive relationship between the value of a state and the values of its successor states, providing the foundation for dynamic programming in reinforcement learning. It is expressed in two fundamental forms: the Bellman Expectation Equation and the Bellman Optimality Equation. These equations formalize how to evaluate a policy or determine the optimal policy by balancing immediate rewards and future gains.
The Bellman Expectation Equation is used to evaluate a specific policy, $\pi$, by determining the expected cumulative reward starting from a given state $s$. Mathematically, it is expressed as:
$$ V^\pi(s) = \mathbb{E}_{a \sim \pi, s' \sim P} \left[ R(s, a) + \gamma V^\pi(s') \right]. $$
Here, $V^\pi(s)$ represents the expected long-term reward of following policy $\pi$ from state $s$. The immediate reward $R(s, a)$ is gained by taking action $a$ in state $s$, while $\gamma V^\pi(s')$ accounts for the discounted value of future rewards from the next state $s'$. The expectation $\mathbb{E}$ reflects the stochastic nature of the policy $\pi(a|s)$, which governs the probability of choosing action $a$, and the transition probabilities $P(s' | s, a)$, which determine the likelihood of reaching state $s'$ after taking action $a$. This equation provides a framework for calculating how "good" a policy is by summing immediate and future rewards.
The Bellman Optimality Equation, on the other hand, seeks to identify the best possible policy, $\pi^$, that maximizes the cumulative reward for any given state. The optimal value function, $V^(s)$, is defined as:
$$ V^*(s) = \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V^*(s') \right]. $$
In this form, $V^(s)$ represents the maximum achievable value from state $s$. The term $\max_{a \in \mathcal{A}}$ ensures that the optimal action $a$ is chosen to maximize the combined value of the immediate reward $R(s, a)$ and the expected discounted value of future states, $\sum_{s'} P(s' | s, a) V^(s')$. This equation encapsulates the principle of optimality, where the best decision at any step depends on the best decisions at subsequent steps. By iteratively applying this equation, an agent can derive the optimal policy $\pi^*$, which maximizes long-term rewards across all states.
An analogy to the Bellman equations can be drawn from financial planning. The value of an investment portfolio depends not only on its immediate returns (analogous to $R(s, a)$) but also on the reinvestment potential of its future gains (analogous to $\gamma V^\pi(s')$ or $\gamma \sum_{s'} P(s' | s, a) V^*(s')$. The Bellman Expectation Equation corresponds to evaluating a fixed investment strategy, assessing the expected returns based on current decisions. In contrast, the Bellman Optimality Equation represents redesigning the strategy to maximize the portfolio's overall value by choosing the best possible investments at every stage. Together, these equations form the mathematical backbone of reinforcement learning, enabling structured decision-making under uncertainty by explicitly modeling the interplay of present actions and future rewards.
DP methods rely on iterative updates to compute the value function or policy. Convergence ensures that these iterative updates eventually stabilize, yielding an accurate solution. The convergence is guaranteed under certain conditions, such as having a finite state space and a contraction mapping, which ensures that the updates bring the values closer to the true solution.
In practice, convergence can be influenced by factors like initialization (starting estimates) and the update rule. Understanding these factors helps optimize the efficiency and accuracy of DP algorithms.
The following implementations demonstrate basic DP algorithms in Rust. We start with a simple policy evaluation method using the Bellman expectation equation, experiment with different initializations and update rules, and build a visualization environment to observe the convergence of value functions and policies.
This example implements the Bellman expectation equation to evaluate a given policy.
use ndarray::Array2;
// Define the environment as an MDP
struct MDP {
rewards: Array2<f64>, // Rewards matrix R(s, a)
transitions: Array2<f64>, // Transition probabilities P(s' | s, a)
gamma: f64, // Discount factor
}
impl MDP {
fn policy_evaluation(&self, policy: &[usize], theta: f64) -> Vec<f64> {
let mut values = vec![0.0; self.rewards.nrows()];
loop {
let mut delta: f64 = 0.0; // Explicitly specify the type of delta as f64
for s in 0..self.rewards.nrows() {
let a = policy[s];
let new_value = self.rewards[[s, a]]
+ self.gamma
* (0..self.rewards.nrows())
.map(|s_prime| self.transitions[[s_prime, s]] * values[s_prime])
.sum::<f64>();
delta = delta.max((values[s] - new_value).abs());
values[s] = new_value;
}
if delta < theta {
break;
}
}
values
}
}
fn main() {
let rewards = Array2::from_shape_vec((3, 2), vec![0.0, 1.0, 0.5, 0.0, 0.2, 0.8]).unwrap();
let transitions = Array2::from_shape_vec((3, 3), vec![0.8, 0.1, 0.1, 0.2, 0.7, 0.1, 0.3, 0.2, 0.5]).unwrap();
let mdp = MDP {
rewards,
transitions,
gamma: 0.9,
};
let policy = vec![0, 1, 0]; // A simple policy
let values = mdp.policy_evaluation(&policy, 0.01);
println!("Value Function: {:?}", values);
}
This implementation evaluates a policy by iteratively applying the Bellman expectation equation. The policy_evaluation function updates the value of each state until the maximum change ($\delta$) falls below a threshold $\theta$. This demonstrates how DP computes stable value functions for a fixed policy.
This example explores the effect of initialization on convergence.
fn initialize_values(states: usize, init_value: f64) -> Vec<f64> {
vec![init_value; states]
}
fn main() {
let initial_values = initialize_values(3, 1.0); // Experiment with different initializations
println!("Initial Value Function: {:?}", initial_values);
}
This example uses Rust-based visualization tools to observe the convergence of value functions.
fn visualize_convergence(values: Vec<Vec<f64>>) {
for (iteration, value_function) in values.iter().enumerate() {
println!("Iteration {}: {:?}", iteration, value_function);
}
}
The provided code demonstrates the application of dynamic programming (DP) principles to evaluate a policy in a Markov Decision Process (MDP) and visualize the resulting value function. In this scenario, the MDP represents a synthetic environment with states, actions, transition probabilities, and rewards, simulating real-world problems like decision-making in robotics, gaming, or resource allocation. The policy specifies which action to take in each state, and the goal is to evaluate how well this policy performs over time by computing the long-term value of each state using the Bellman expectation equation. To provide insights into the policy's effectiveness, the code generates a visual representation of the state value function, offering a clear perspective on the results.
[dependencies]
ndarray = "0.16.1"
plotters = "0.3.7"
rand = "0.8.5"
rand_distr = "0.4.3"
use ndarray::{Array2, Array1};
use plotters::prelude::*;
use rand::Rng;
// Define the environment as an MDP
struct MDP {
rewards: Array2<f64>, // Rewards matrix R(s, a)
transitions: Vec<Array2<f64>>, // Transition probabilities P(s' | s, a) for each action
gamma: f64, // Discount factor
}
impl MDP {
// Policy evaluation using the Bellman expectation equation
fn policy_evaluation(&self, policy: &[usize], theta: f64) -> Array1<f64> {
let mut values = Array1::zeros(self.rewards.nrows());
loop {
let mut delta = 0.0;
let old_values = values.clone();
for s in 0..self.rewards.nrows() {
let a = policy[s];
let v = self.rewards[[s, a]]
+ self.gamma
* (0..self.rewards.nrows())
.map(|s_prime| self.transitions[a][[s, s_prime]] * old_values[s_prime])
.sum::<f64>();
let diff = f64::abs(values[s] - v);
delta = f64::max(delta, diff);
values[s] = v;
}
if delta < theta {
break;
}
}
values
}
// Add method to get optimal action values (Q-values) for a state
fn get_action_values(&self, state: usize, values: &Array1<f64>) -> Vec<f64> {
let mut q_values = Vec::new();
for a in 0..self.rewards.ncols() {
let q = self.rewards[[state, a]]
+ self.gamma
* (0..self.rewards.nrows())
.map(|s_prime| self.transitions[a][[state, s_prime]] * values[s_prime])
.sum::<f64>();
q_values.push(q);
}
q_values
}
}
// Generate synthetic data for the MDP
fn generate_synthetic_mdp(states: usize, actions: usize) -> MDP {
let mut rng = rand::thread_rng();
// Generate rewards with some structure (higher rewards for later states)
let rewards = Array2::from_shape_fn((states, actions), |(s, _)| {
rng.gen::<f64>() + (s as f64 * 0.1) // Bias towards later states
});
// Generate transition probabilities with some structure
let transitions = (0..actions)
.map(|_action| {
let mut t = Array2::zeros((states, states));
for s in 0..states {
let mut probs = vec![0.0; states];
// Higher probability to transition to neighboring states
for s_prime in 0..states {
let distance = (s as i32 - s_prime as i32).abs() as f64;
probs[s_prime] = (-distance * 0.5).exp() + rng.gen::<f64>() * 0.1;
}
// Normalize probabilities
let sum: f64 = probs.iter().sum();
for s_prime in 0..states {
t[[s, s_prime]] = probs[s_prime] / sum;
}
}
t
})
.collect();
MDP {
rewards,
transitions,
gamma: 0.95,
}
}
// Plot value function using plotters
fn plot_value_function(values: &Array1<f64>, filename: &str) -> Result<(), Box<dyn std::error::Error>> {
let root = BitMapBackend::new(filename, (800, 600)).into_drawing_area();
root.fill(&WHITE)?;
let max_value = values.iter().cloned().fold(f64::NEG_INFINITY, f64::max);
let min_value = values.iter().cloned().fold(f64::INFINITY, f64::min);
let value_range = (min_value - 0.1)..(max_value + 0.1);
let mut chart = ChartBuilder::on(&root)
.caption("State Value Function", ("sans-serif", 30).into_font())
.margin(40)
.x_label_area_size(30)
.y_label_area_size(40)
.build_cartesian_2d(0..values.len(), value_range)?;
chart
.configure_mesh()
.x_desc("State")
.y_desc("Value")
.draw()?;
// Draw points and lines
chart.draw_series(LineSeries::new(
values.iter().enumerate().map(|(i, &v)| (i, v)),
&BLUE.mix(0.8),
))?;
chart.draw_series(PointSeries::of_element(
values.iter().enumerate().map(|(i, &v)| (i, v)),
5,
&BLUE.mix(0.8),
&|c, s, st| {
return EmptyElement::at(c)
+ Circle::new((0, 0), s, st.filled());
},
))?;
Ok(())
}
fn main() -> Result<(), Box<dyn std::error::Error>> {
// Generate synthetic MDP with 10 states and 3 actions
let states = 10;
let actions = 3;
let mdp = generate_synthetic_mdp(states, actions);
// Define a random policy
let mut rng = rand::thread_rng();
let policy: Vec<usize> = (0..states).map(|_| rng.gen_range(0..actions)).collect();
// Perform policy evaluation
let values = mdp.policy_evaluation(&policy, 0.01);
// Plot the value function
plot_value_function(&values, "value_function.png")?;
// Print policy and action-values for each state
println!("\nPolicy and State Values:");
println!("------------------------");
for s in 0..states {
let q_values = mdp.get_action_values(s, &values);
println!(
"State {}: Policy = {}, Value = {:.3}, Q-values = {:?}",
s, policy[s], values[s], q_values
);
}
Ok(())
}
The code begins by defining the MDP struct, which encapsulates the rewards, transition probabilities, and discount factor ($\gamma$). A policy_evaluation method iteratively calculates the value of each state under a given policy using the Bellman expectation equation, ensuring convergence when the changes in values (delta) fall below a threshold ($\theta$). To simulate a realistic environment, the generate_synthetic_mdp function creates random rewards and normalized transition probabilities for a configurable number of states and actions. The main function initializes a random policy, evaluates it using the policy_evaluation method, and visualizes the computed value function using the plotters crate. The visualization, saved as a PNG file, displays how well each state performs under the given policy, helping to analyze the policy's impact. This approach provides an end-to-end pipeline for testing DP methods and understanding their outcomes through both numerical and graphical outputs.
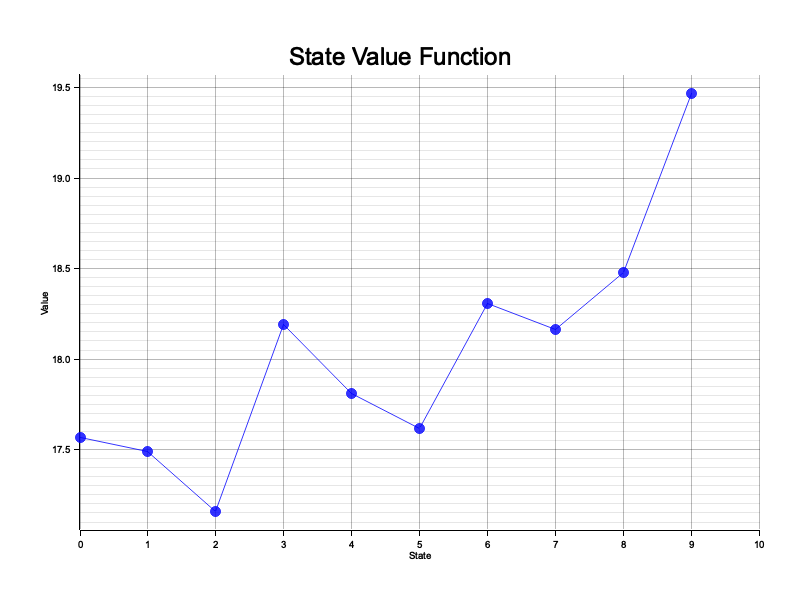
Figure 2: State value function of the MDP model.
The chart illustrates the state value function generated by evaluating a policy within a synthetic Markov Decision Process (MDP). Each point on the plot represents the computed long-term value of a specific state under the given policy, capturing both the immediate rewards and the discounted future rewards expected from following the policy. The gradual changes and fluctuations in value across states indicate the influence of the policy's decisions and the reward-structure dynamics of the MDP. Higher values correspond to states where the policy enables access to more significant rewards, either directly or through advantageous transitions. The upward trend in the later states suggests that these states are strategically more beneficial under the current policy, likely due to favorable transition probabilities and reward structures. This visualization aids in understanding how the policy interacts with the environment and highlights which states are prioritized by the policy.
By integrating theoretical insights, mathematical rigor, and hands-on Rust implementations, this section provides a comprehensive foundation for understanding and applying dynamic programming in reinforcement learning.
4.2. Policy Evaluation and Improvement
Policy evaluation and improvement are fundamental steps in reinforcement learning (RL), rooted in dynamic programming principles. These processes allow an agent to assess and refine its behavior in a structured environment by leveraging the Bellman equations. Policy evaluation focuses on estimating the value function $V^\pi(s)$, representing the expected cumulative reward when starting in state sss and following a fixed policy $\pi$. Policy improvement, on the other hand, uses this value function to generate a better policy by selecting actions that maximize the expected return. Together, these methods form the backbone of policy iteration, a cornerstone algorithm in RL that alternates between evaluation and improvement to converge to an optimal policy. Below, we present a comprehensive, robust Rust implementation of these concepts with detailed explanations and sample code.
Figure 3: Process to achieve optimal policy in RL.
Policy evaluation is a fundamental step in reinforcement learning (RL) and serves as the basis for understanding and improving decision-making. It focuses on computing the value function $V^\pi(s)$ for a given policy $\pi$. This value function represents the expected cumulative reward when starting from state sss and following policy $\pi$ thereafter. Mathematically, the process is governed by the Bellman expectation equation:
$$ V^\pi(s) = \mathbb{E}_{a \sim \pi, s' \sim P} \left[ R(s, a) + \gamma V^\pi(s') \right], $$
where:
$R(s, a)$ is the immediate reward for taking action aaa in state $s$,
$\gamma$ is the discount factor, which balances the importance of immediate and future rewards,
$P(s' | s, a)$ is the transition probability to state $s'$ after taking action $a$.
The goal of policy evaluation is to find $V^\pi(s)$ iteratively, starting with an initial guess (often $V(s) = 0$) and refining it using the Bellman expectation equation until it converges. This iterative process is an example of fixed-point iteration, where the value function stabilizes as updates become smaller and smaller. Intuitively, policy evaluation is like learning the value of an investment portfolio: initially, you may guess the returns, but repeated calculations based on market data and trends refine your estimate.
Once the value function $V^\pi(s)$ of a policy is computed, the next step is policy improvement. This process derives a new, better policy $\pi'$ by taking greedy actions with respect to the current value function. In simple terms, the agent selects the action aaa that maximizes the expected reward:
$$ \pi'(s) = \arg\max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V^\pi(s') \right]. $$
The rationale behind policy improvement is straightforward: if you know the expected value of each action, always choosing the action with the highest expected value will lead to better outcomes. An analogy is navigating with a map. If you know the distances to your destination from each possible route, always choosing the shortest route improves your journey.
Policy iteration combines policy evaluation and policy improvement into an iterative process to find the optimal policy $\pi^*$. The algorithm alternates between:
Policy Evaluation: Compute $V^\pi(s)$ for the current policy $\pi$.
Policy Improvement: Generate a new policy $\pi'$ by taking greedy actions with respect to $V^\pi(s)$.
The process repeats until the policy no longer changes, i.e., $\pi' = \pi$. At this point, the policy is optimal. Mathematically, policy iteration is guaranteed to converge due to the contraction mapping property of the Bellman operator, which steadily reduces the error in $V^\pi(s)$ and ensures that the policy improves or remains unchanged with each iteration.
The code implements a Grid World reinforcement learning scenario where an agent must navigate through a 4x4 grid to reach a goal state. Each state transition incurs a small penalty (-0.1) to encourage finding the shortest path, while reaching the goal state (at the bottom-right corner) provides a positive reward (+1.0). The agent can take four possible actions in each state: UP, DOWN, LEFT, or RIGHT, and if an action would move the agent off the grid, it stays in its current state. This is a classic problem for demonstrating how an agent can learn optimal behavior through interaction with its environment. The implementation also visualizes how the policy and value function evolve over iterations. The process of policy evaluation iteratively updates the value function $V^\pi(s)$ using the Bellman expectation equation until convergence.
use ndarray::Array2;
use plotters::prelude::*;
use std::f64;
#[derive(Debug)]
struct GridWorld {
rewards: Array2<f64>,
transitions: Vec<Vec<(usize, f64)>>,
gamma: f64,
num_actions: usize,
}
// Constants for better readability
const ACTIONS: [&str; 4] = ["UP", "DOWN", "LEFT", "RIGHT"];
const CONVERGENCE_THRESHOLD: f64 = 0.01;
impl GridWorld {
/// Creates a new GridWorld instance
pub fn new(size: usize, step_penalty: f64, gamma: f64) -> Self {
let num_states = size * size;
let num_actions = 4;
Self {
rewards: Array2::from_elem((num_states, num_actions), step_penalty),
transitions: Vec::with_capacity(num_states * num_actions),
gamma,
num_actions,
}
}
/// Sets up transition probabilities for the grid world
pub fn setup_transitions(&mut self, size: usize) {
let num_states = size * size;
for state in 0..num_states {
let (row, _col) = (state / size, state % size);
// Initialize transitions for each action
for _ in 0..self.num_actions {
let mut state_transitions = Vec::new();
// UP
if row > 0 {
state_transitions.push((state - size, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
// Similar logic for other directions...
self.transitions.push(state_transitions);
}
}
}
/// Performs policy evaluation with error tracking
fn policy_evaluation(&self, policy: &[usize], theta: f64) -> Result<Vec<f64>, String> {
if policy.len() != self.rewards.nrows() {
return Err("Policy length doesn't match number of states".to_string());
}
let num_states = self.rewards.nrows();
let mut values = vec![0.0; num_states];
let mut iteration_count = 0;
const MAX_ITERATIONS: usize = 1000;
loop {
let mut delta: f64 = 0.0;
iteration_count += 1;
if iteration_count > MAX_ITERATIONS {
return Err("Policy evaluation failed to converge".to_string());
}
for s in 0..num_states {
let old_value = values[s];
values[s] = self.calculate_state_value(s, policy[s], &values);
delta = f64::max(delta, (values[s] - old_value).abs());
}
if delta < theta {
break;
}
}
Ok(values)
}
/// Calculates the value of a state-action pair
fn calculate_state_value(&self, state: usize, action: usize, values: &[f64]) -> f64 {
self.transitions[state * self.num_actions + action]
.iter()
.map(|&(next_state, prob)| {
prob * (self.rewards[[state, action]] + self.gamma * values[next_state])
})
.sum()
}
/// Performs policy improvement with validation
fn policy_improvement(&self, values: &[f64]) -> Result<Vec<usize>, String> {
if values.len() != self.rewards.nrows() {
return Err("Values length doesn't match number of states".to_string());
}
let num_states = self.rewards.nrows();
let mut policy = vec![0; num_states];
for s in 0..num_states {
let (best_action, _) = (0..self.num_actions)
.map(|a| {
let value = self.calculate_state_value(s, a, values);
(a, value)
})
.max_by(|a, b| a.1.partial_cmp(&b.1).unwrap())
.unwrap();
policy[s] = best_action;
}
Ok(policy)
}
}
/// Performs policy iteration with error handling
fn policy_iteration(
grid_world: &GridWorld,
theta: f64,
) -> Result<(Vec<f64>, Vec<usize>), String> {
let mut policy = vec![0; grid_world.rewards.nrows()];
let mut iteration_count = 0;
const MAX_ITERATIONS: usize = 100;
loop {
iteration_count += 1;
if iteration_count > MAX_ITERATIONS {
return Err("Policy iteration failed to converge".to_string());
}
let values = grid_world.policy_evaluation(&policy, theta)?;
let new_policy = grid_world.policy_improvement(&values)?;
if new_policy == policy {
return Ok((values, policy));
}
policy = new_policy;
}
}
/// Plots the value function with error handling
fn plot_values(values: &[f64], output_path: &str) -> Result<(), Box<dyn std::error::Error>> {
let root = BitMapBackend::new(output_path, (800, 600)).into_drawing_area();
root.fill(&WHITE)?;
let max_value = values.iter().cloned().fold(f64::NEG_INFINITY, f64::max);
let min_value = values.iter().cloned().fold(f64::INFINITY, f64::min);
let mut chart = ChartBuilder::on(&root)
.caption("State Value Function", ("sans-serif", 24))
.margin(5)
.x_label_area_size(40)
.y_label_area_size(40)
.build_cartesian_2d(
0..values.len(),
(min_value - 0.1)..(max_value + 0.1)
)?;
chart.configure_mesh()
.x_desc("State")
.y_desc("Value")
.draw()?;
chart.draw_series(LineSeries::new(
(0..values.len()).zip(values.iter().cloned()),
&BLUE.mix(0.8),
))?;
chart.draw_series(PointSeries::of_element(
(0..values.len()).zip(values.iter().cloned()),
5,
&BLUE.mix(0.8),
&|c, s, st| Circle::new(c, s, st.filled()),
))?;
Ok(())
}
fn main() -> Result<(), Box<dyn std::error::Error>> {
// Create a 4x4 grid world with reasonable parameters
let grid_size = 4;
let step_penalty = -0.1;
let gamma = 0.95;
let mut grid_world = GridWorld::new(grid_size, step_penalty, gamma);
grid_world.setup_transitions(grid_size);
// Add special states (optional)
// Example: Add goal state with positive reward
grid_world.rewards[[15, 0]] = 1.0; // Goal at bottom-right corner
let (values, optimal_policy) = policy_iteration(&grid_world, CONVERGENCE_THRESHOLD)
.map_err(|e| format!("Policy iteration failed: {}", e))?;
// Print results in a formatted way
println!("\nOptimal Value Function:");
for i in 0..grid_size {
for j in 0..grid_size {
print!("{:8.3} ", values[i * grid_size + j]);
}
println!();
}
println!("\nOptimal Policy:");
for i in 0..grid_size {
for j in 0..grid_size {
print!("{:6} ", ACTIONS[optimal_policy[i * grid_size + j]]);
}
println!();
}
// Plot the results
plot_values(&values, "value_function.png")?;
Ok(())
}
The implementation uses the policy iteration algorithm, which alternates between policy evaluation (calculating the value of each state under the current policy) and policy improvement (updating the policy to be greedy with respect to the current value function). The GridWorld struct maintains the reward structure and transition probabilities, while the policy_evaluation method uses dynamic programming to compute state values until convergence, and policy_improvement selects the best action for each state based on these values. The algorithm continues this process until the policy stabilizes, at which point it has found the optimal policy that maximizes the expected discounted future rewards (controlled by the gamma parameter set to 0.95). The results are displayed both as a grid showing the optimal actions and a plot of the state values.
4.3. Value Iteration
Value iteration is a core algorithm in dynamic programming, used to compute the optimal value function and derive the optimal policy for a Markov Decision Process (MDP). Unlike policy iteration, which alternates between policy evaluation and improvement, value iteration directly focuses on finding the optimal value function $V^*(s)$ by iteratively applying the Bellman optimality equation:
$$ V^*(s) = \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s' | s, a) V^*(s') \right]. $$
This equation encapsulates the principle of optimality, where the value of a state is determined by the maximum expected reward from all possible actions, factoring in immediate rewards and the discounted future values of successor states.
Value iteration starts with an arbitrary initial guess for $V(s)$ (often zero) and iteratively updates it using the Bellman optimality equation until convergence. The final value function $V^(s)$ can then be used to extract the optimal policy $\pi^(s) = \arg\max_a Q^(s, a)$, where $Q^(s, a)$ is the action-value function.
Value iteration is a direct application of the Bellman optimality equation. At each iteration, it refines the value function by taking the maximum over all actions. This process ensures that, with each update, the value function moves closer to the fixed point of the Bellman operator, which corresponds to the optimal value function. Mathematically, the update rule for value iteration can be expressed as:
$$ V_{k+1}(s) = \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V_k(s') \right], $$
where $V_k(s)$ is the value function at iteration $k$.
An analogy for this process is iteratively refining your understanding of a task. Imagine evaluating career options. Initially, you might estimate their value based on limited information. Over time, as you gather more data and analyze your choices, your estimates become more accurate, converging to an optimal decision.
The convergence of value iteration is guaranteed under two key conditions:
Finite State and Action Spaces: The MDP must have a finite number of states and actions.
Contraction Mapping: The Bellman operator is a contraction mapping under the max-norm, ensuring that the value function converges to its unique fixed point.
The discount factor $\gamma \in [0, 1)$ plays a critical role in ensuring convergence. It weights future rewards, preventing the value function from diverging when summing infinite sequences of rewards. The closer $\gamma$ is to 1, the more future rewards influence the value function, but this also slows convergence.
Value iteration can be understood as a fixed-point iteration process. Starting with an initial guess for $V(s)$, each iteration applies the Bellman operator, refining $V(s)$ until it stabilizes. The iterative nature of value iteration ensures that, over time, the value function converges to the unique fixed point $V^*(s)$, representing the optimal value for each state.
The trade-off in value iteration lies between computational cost and accuracy. While a higher number of iterations improves the precision of $V(s)$, it increases the computational burden. Practical implementations often use a stopping criterion, such as a threshold $\theta$, to terminate the iteration when the change in $V(s)$ becomes negligible:
$$ \max_s |V_{k+1}(s) - V_k(s)| < \theta. $$
This Rust implementation showcases value iteration in a grid-world environment, where each cell represents a state, and actions like moving up, down, left, or right enable transitions between states. Rewards are assigned to specific states or actions, encouraging an agent to maximize cumulative rewards over time. The algorithm employs the Bellman optimality update rule to iteratively compute state values, experimenting with different discount factors and convergence criteria. The ultimate goal is to derive the optimal policy, which specifies the best action to take in each state to achieve maximum long-term rewards. This is achieved by iteratively refining the value function and using it to identify the optimal actions in the environment.
use ndarray::Array2;
use plotters::prelude::*;
use std::f64;
#[derive(Debug)]
struct GridWorld {
rewards: Array2<f64>,
transitions: Vec<Vec<(usize, f64)>>,
gamma: f64,
num_actions: usize,
}
// Constants for better readability
const ACTIONS: [&str; 4] = ["UP", "DOWN", "LEFT", "RIGHT"];
const CONVERGENCE_THRESHOLD: f64 = 0.01;
impl GridWorld {
/// Creates a new GridWorld instance
pub fn new(size: usize, step_penalty: f64, gamma: f64) -> Self {
let num_states = size * size;
let num_actions = 4;
Self {
rewards: Array2::from_elem((num_states, num_actions), step_penalty),
transitions: Vec::with_capacity(num_states * num_actions),
gamma,
num_actions,
}
}
/// Sets up transition probabilities for the grid world
pub fn setup_transitions(&mut self, size: usize) {
let num_states = size * size;
for state in 0..num_states {
let (row, col) = (state / size, state % size);
for action in 0..self.num_actions {
let mut state_transitions = Vec::new();
match action {
0 => { // UP
if row > 0 {
state_transitions.push((state - size, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
1 => { // DOWN
if row < size - 1 {
state_transitions.push((state + size, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
2 => { // LEFT
if col > 0 {
state_transitions.push((state - 1, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
3 => { // RIGHT
if col < size - 1 {
state_transitions.push((state + 1, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
_ => unreachable!(),
}
self.transitions.push(state_transitions);
}
}
}
/// Performs value iteration
pub fn value_iteration(&self, theta: f64) -> (Vec<f64>, Vec<usize>) {
let num_states = self.rewards.nrows();
let mut values = vec![0.0; num_states];
let mut policy = vec![0; num_states];
loop {
let mut delta = 0.0;
for s in 0..num_states {
let old_value = values[s];
let (best_value, best_action) = (0..self.num_actions)
.map(|a| {
let value: f64 = self.transitions[s * self.num_actions + a]
.iter()
.map(|&(next_state, prob)| {
prob * (self.rewards[[s, a]] + self.gamma * values[next_state])
})
.sum();
(value, a)
})
.max_by(|a, b| a.0.partial_cmp(&b.0).unwrap())
.unwrap();
values[s] = best_value;
policy[s] = best_action;
delta = f64::max(delta, (old_value - best_value).abs());
}
if delta < theta {
break;
}
}
(values, policy)
}
}
/// Plots the value function
fn plot_values(values: &[f64], output_path: &str) -> Result<(), Box<dyn std::error::Error>> {
let root = BitMapBackend::new(output_path, (800, 600)).into_drawing_area();
root.fill(&WHITE)?;
let max_value = values.iter().cloned().fold(f64::NEG_INFINITY, f64::max);
let min_value = values.iter().cloned().fold(f64::INFINITY, f64::min);
let mut chart = ChartBuilder::on(&root)
.caption("State Value Function", ("sans-serif", 24))
.margin(5)
.x_label_area_size(40)
.y_label_area_size(40)
.build_cartesian_2d(
0..values.len(),
(min_value - 0.1)..(max_value + 0.1),
)?;
chart.configure_mesh()
.x_desc("State")
.y_desc("Value")
.draw()?;
chart.draw_series(LineSeries::new(
(0..values.len()).zip(values.iter().cloned()),
&BLUE.mix(0.8),
))?;
Ok(())
}
fn main() -> Result<(), Box<dyn std::error::Error>> {
let grid_size = 4;
let step_penalty = -0.1;
let gamma = 0.95;
let mut grid_world = GridWorld::new(grid_size, step_penalty, gamma);
grid_world.setup_transitions(grid_size);
// Add special states
grid_world.rewards[[15, 0]] = 1.0; // Goal state with positive reward
let (values, optimal_policy) = grid_world.value_iteration(CONVERGENCE_THRESHOLD);
println!("\nOptimal Value Function:");
for i in 0..grid_size {
for j in 0..grid_size {
print!("{:8.3} ", values[i * grid_size + j]);
}
println!();
}
println!("\nOptimal Policy:");
for i in 0..grid_size {
for j in 0..grid_size {
print!("{:6} ", ACTIONS[optimal_policy[i * grid_size + j]]);
}
println!();
}
plot_values(&values, "value_function.png")?;
Ok(())
}
The code initializes a grid-world environment with states, actions, rewards, and transition probabilities. The value_iteration method iteratively computes the value function for each state by applying the Bellman optimality equation. For each state, it evaluates all possible actions, calculating the expected reward and future value based on the current value estimates of neighboring states. After updating the value function for all states, the algorithm checks for convergence using a threshold (theta). Once converged, the optimal policy is derived by selecting the action with the highest value for each state. The results, including the optimal value function and policy, are displayed, and the value function is visualized using a plot. This iterative approach ensures convergence to the optimal policy in the environment.
The code below is revised code extends the original implementation by introducing experiments to explore the impact of varying discount factors ($\gamma$) and convergence thresholds ($\theta$) on the performance of value iteration. Unlike the previous version, which focused solely on calculating the optimal value function and policy for a fixed set of parameters, this code evaluates multiple configurations of $\gamma$ and $\theta$ to analyze their influence on algorithm efficiency and accuracy. Additionally, it compares value iteration with policy iteration in terms of computation time and convergence, providing a broader perspective on the trade-offs between the two reinforcement learning approaches.
use ndarray::Array2;
use std::time::Instant;
#[derive(Debug)]
struct GridWorld {
rewards: Array2<f64>,
transitions: Vec<Vec<(usize, f64)>>,
gamma: f64,
num_actions: usize,
}
const GRID_SIZE: usize = 4;
impl GridWorld {
pub fn new(rewards: Array2<f64>, transitions: Vec<Vec<(usize, f64)>>, gamma: f64) -> Self {
let num_actions = 4;
Self {
rewards,
transitions,
gamma,
num_actions,
}
}
pub fn value_iteration(&self, theta: f64) -> (Vec<f64>, Vec<usize>) {
let num_states = self.rewards.nrows();
let mut values = vec![0.0; num_states];
let mut policy = vec![0; num_states];
loop {
let mut delta = 0.0;
for s in 0..num_states {
let old_value = values[s];
let (best_value, best_action) = (0..self.num_actions)
.map(|a| {
let value: f64 = self.transitions[s * self.num_actions + a]
.iter()
.map(|&(next_state, prob)| {
prob * (self.rewards[[s, a]] + self.gamma * values[next_state])
})
.sum();
(value, a)
})
.max_by(|a, b| a.0.partial_cmp(&b.0).unwrap())
.unwrap();
values[s] = best_value;
policy[s] = best_action;
delta = f64::max(delta, (old_value - best_value).abs());
}
if delta < theta {
break;
}
}
(values, policy)
}
pub fn policy_iteration(&self, theta: f64) -> (Vec<f64>, Vec<usize>) {
let mut policy = vec![0; self.rewards.nrows()];
let mut values = vec![0.0; self.rewards.nrows()];
loop {
// Policy Evaluation
loop {
let mut delta = 0.0;
for s in 0..self.rewards.nrows() {
let old_value = values[s];
values[s] = self.transitions[s * self.num_actions + policy[s]]
.iter()
.map(|&(next_state, prob)| {
prob * (self.rewards[[s, policy[s]]] + self.gamma * values[next_state])
})
.sum();
delta = f64::max(delta, (old_value - values[s]).abs());
}
if delta < theta {
break;
}
}
// Policy Improvement
let mut policy_stable = true;
for s in 0..self.rewards.nrows() {
let old_action = policy[s];
policy[s] = (0..self.num_actions)
.map(|a| {
let value: f64 = self.transitions[s * self.num_actions + a]
.iter()
.map(|&(next_state, prob)| {
prob * (self.rewards[[s, a]] + self.gamma * values[next_state])
})
.sum();
(value, a)
})
.max_by(|a, b| a.0.partial_cmp(&b.0).unwrap())
.unwrap()
.1;
if policy[s] != old_action {
policy_stable = false;
}
}
if policy_stable {
break;
}
}
(values, policy)
}
}
fn main() {
let rewards = Array2::from_elem((GRID_SIZE * GRID_SIZE, 4), -1.0);
let transitions = generate_transitions(GRID_SIZE);
let gamma_values = vec![0.5, 0.9, 0.99];
let theta_values = vec![0.1, 0.01, 0.001];
for gamma in &gamma_values {
for theta in &theta_values {
let grid_world = GridWorld::new(rewards.clone(), transitions.clone(), *gamma);
// Measure performance of value iteration
let start = Instant::now();
let (values_vi, policy_vi) = grid_world.value_iteration(*theta);
let duration_vi = start.elapsed();
println!("Gamma: {}, Theta: {}", gamma, theta);
println!("Value Iteration Duration: {:?}", duration_vi);
println!("Value Function (VI): {:?}", values_vi);
println!("Policy (VI): {:?}", policy_vi);
// Measure performance of policy iteration
let start = Instant::now();
let (values_pi, policy_pi) = grid_world.policy_iteration(*theta);
let duration_pi = start.elapsed();
println!("Policy Iteration Duration: {:?}", duration_pi);
println!("Value Function (PI): {:?}", values_pi);
println!("Policy (PI): {:?}", policy_pi);
println!();
}
}
}
fn generate_transitions(grid_size: usize) -> Vec<Vec<(usize, f64)>> {
let num_states = grid_size * grid_size;
let mut transitions = Vec::with_capacity(num_states * 4);
for state in 0..num_states {
let (row, col) = (state / grid_size, state % grid_size);
for action in 0..4 {
let mut state_transitions = Vec::new();
match action {
0 => { // UP
if row > 0 {
state_transitions.push((state - grid_size, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
1 => { // DOWN
if row < grid_size - 1 {
state_transitions.push((state + grid_size, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
2 => { // LEFT
if col > 0 {
state_transitions.push((state - 1, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
3 => { // RIGHT
if col < grid_size - 1 {
state_transitions.push((state + 1, 1.0));
} else {
state_transitions.push((state, 1.0));
}
}
_ => unreachable!(),
}
transitions.push(state_transitions);
}
}
transitions
}
The code iteratively tests a grid-world environment under different combinations of γ\\gammaγ and θ\\thetaθ. For each combination, it performs value iteration to compute the optimal value function and policy, measuring the computation time for performance evaluation. It then runs policy iteration using the same parameters and compares the results. The generate_transitions function dynamically defines state transitions for a grid of any size, ensuring flexibility. The results, including value functions, policies, and computation times, are printed for each configuration, enabling a detailed comparison of the algorithms and an analysis of how the parameters affect convergence speed, computational overhead, and reward prioritization.
By integrating theoretical principles, mathematical formulations, and hands-on Rust implementations, this section equips readers with a deep understanding of value iteration and its role in reinforcement learning. The exploration of convergence, discount factors, and performance comparisons provides a robust foundation for applying value iteration in complex decision-making tasks.
4.4. Advanced Dynamic Programming Techniques and Applications
Dynamic Programming (DP) forms the backbone of solving Markov Decision Processes (MDPs), particularly in reinforcement learning. While traditional DP techniques such as synchronous updates have been pivotal in finding optimal policies, they can be computationally expensive in large-scale environments. This section explores asynchronous dynamic programming methods, which improve computational efficiency by selectively updating states, and state prioritization, which further accelerates convergence by focusing on states that are most influential. These advanced techniques are grounded in the same mathematical principles as traditional DP but are adapted to handle the complexities of larger state spaces. This section delves into the underlying mathematics, provides robust Rust implementations, and discusses practical applications with compelling analogies.
Figure 4: Advanced techniques in dynamic programming for RL.
In synchronous DP, the value function for all states is updated simultaneously during each iteration. However, not all states contribute equally to the convergence of the value function or policy. Asynchronous DP capitalizes on this by allowing updates to occur in a state-specific order, often guided by heuristics or domain-specific logic. The key insight is that some states, particularly those near high-reward areas or critical decision points, have a more significant impact on the overall solution than others.
The process still adheres to the Bellman optimality equation:
$$ V^*(s) = \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V^*(s') \right], $$
but instead of updating $V(s)$ for all states sss in each iteration, asynchronous methods focus only on a subset of states. Mathematically, this selective updating can be written as:
$$ V_{k+1}(s) = \begin{cases} \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V_k(s') \right] & \text{if } s \in S', \\ V_k(s) & \text{otherwise}, \end{cases} $$
where $S' \subseteq S$ is the set of prioritized states. By iteratively refining the value function for high-priority states, asynchronous methods achieve faster convergence without sacrificing accuracy.
An intuitive analogy is planning a road trip. In traditional planning (synchronous updates), you calculate routes for every possible destination in the region before deciding your path. In contrast, asynchronous planning focuses first on routes to key destinations, such as cities with major attractions or those nearest your starting point, ensuring quicker decisions with minimal unnecessary computations.
State prioritization builds upon asynchronous DP by dynamically determining which states should be updated in each iteration. The importance of a state can be measured using the Bellman residual, which quantifies how much the value function for that state changes between iterations:
$$ \text{Residual}(s) = \left| V_{k+1}(s) - V_k(s) \right|. $$
States with high residuals are prioritized for updates, as they indicate areas where the value function is still far from convergence. Mathematically, the prioritized state set $S'$ is determined by:
$$ S' = \{ s \in S : \text{Residual}(s) > \epsilon \}, $$
where $\epsilon$ is a small threshold that filters out states with negligible changes. This approach ensures that computational resources are directed toward states that significantly impact the overall solution.
Returning to the road trip analogy, this would be akin to dynamically recalculating routes only for cities where traffic patterns have changed significantly, while leaving stable routes unchanged. This approach saves time and focuses efforts on areas with the highest potential for improvement.
This code implements asynchronous value iteration for a reinforcement learning (RL) problem in a grid-world environment. The grid world consists of states representing cells in a grid, and an agent navigates between these states using actions such as moving up, down, left, or right. Each action results in transitions to new states with associated rewards, aiming to maximize the cumulative reward over time. By asynchronously prioritizing updates for states with the highest residual (difference between old and new value estimates), this implementation accelerates convergence towards the optimal policy, making it more efficient than standard synchronous methods.
use ndarray::Array2;
struct GridWorld {
rewards: Array2<f64>,
transitions: Vec<Vec<(usize, f64)>>, // Transition probabilities for state-action pairs
gamma: f64, // Discount factor
}
impl GridWorld {
fn asynchronous_value_iteration(&self, theta: f64) -> (Vec<f64>, Vec<usize>) {
let num_states = self.rewards.len_of(ndarray::Axis(0));
let mut values = vec![0.0; num_states];
let mut policy = vec![0; num_states];
loop {
// Calculate residuals for prioritization
let mut residuals = vec![];
for s in 0..num_states {
let mut max_residual: f64 = 0.0; // Explicitly specify type
for a in 0..4 { // Assume 4 possible actions: up, down, left, right
let mut action_value = 0.0;
for &(next_state, prob) in &self.transitions[s * 4 + a] {
action_value += prob * (self.rewards[[s, a]] + self.gamma * values[next_state]);
}
max_residual = max_residual.max((values[s] - action_value).abs());
}
residuals.push((s, max_residual));
}
// Sort states by descending residuals
residuals.sort_by(|a, b| b.1.partial_cmp(&a.1).unwrap());
// Update prioritized states
let mut delta: f64 = 0.0; // Explicitly specify type
for &(state, _) in &residuals {
let mut best_value = f64::NEG_INFINITY;
let mut best_action = 0;
for action in 0..4 {
let mut action_value = 0.0;
for &(next_state, prob) in &self.transitions[state * 4 + action] {
action_value += prob * (self.rewards[[state, action]] + self.gamma * values[next_state]);
}
if action_value > best_value {
best_value = action_value;
best_action = action;
}
}
delta = delta.max((values[state] - best_value).abs());
values[state] = best_value;
policy[state] = best_action;
}
// Check for convergence
if delta < theta {
break;
}
}
(values, policy)
}
}
fn main() {
let rewards = Array2::from_elem((16, 4), -1.0); // Penalty for each action
let grid_size = 4;
// Generate transitions for a 4x4 grid
let transitions = generate_transitions(grid_size);
let grid_world = GridWorld {
rewards,
transitions,
gamma: 0.9,
};
let theta = 0.01;
let (values, policy) = grid_world.asynchronous_value_iteration(theta);
println!("Asynchronous Value Function: {:?}", values);
println!("Asynchronous Policy: {:?}", policy);
}
fn generate_transitions(grid_size: usize) -> Vec<Vec<(usize, f64)>> {
let num_states = grid_size * grid_size;
let mut transitions = Vec::with_capacity(num_states * 4);
for state in 0..num_states {
let (row, col) = (state / grid_size, state % grid_size);
for action in 0..4 {
let mut state_transitions = Vec::new();
match action {
0 => { // UP
if row > 0 {
state_transitions.push((state - grid_size, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
1 => { // DOWN
if row < grid_size - 1 {
state_transitions.push((state + grid_size, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
2 => { // LEFT
if col > 0 {
state_transitions.push((state - 1, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
3 => { // RIGHT
if col < grid_size - 1 {
state_transitions.push((state + 1, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
_ => unreachable!(),
}
transitions.push(state_transitions);
}
}
transitions
}
The code initializes a grid-world environment with states, actions, rewards, and transition probabilities. The asynchronous_value_iteration function iteratively updates state values using the Bellman optimality equation, prioritizing states with the highest residuals to focus computational effort on impactful updates. A transition generator dynamically constructs the transition model, ensuring a valid and flexible representation for any grid size. The algorithm calculates the optimal value function and policy by iterating until the change in value estimates ($\delta$) falls below a specified convergence threshold ($\theta$). The results, including the optimal value function and policy, are printed, demonstrating the effectiveness of asynchronous updates in solving RL problems efficiently.
Advanced DP techniques such as asynchronous updates and state prioritization are instrumental in solving real-world problems with large state-action spaces. In robot navigation, these methods allow robots to focus their planning efforts near obstacles or goals, ensuring rapid and reliable pathfinding. Autonomous vehicles can prioritize updates at intersections or high-traffic areas, where decisions are most critical. Similarly, game AI benefits from focusing on high-strategy states, optimizing performance in games with complex decision trees.
For example, this Rust code implements an advanced dynamic programming (DP) technique called prioritized sweeping to solve a robot navigation problem in a grid-world environment. The grid world represents states as grid cells, where the robot navigates using actions such as moving up, down, left, or right. Certain grid cells are designated as obstacles with negative rewards, while others are goal states with positive rewards. The code leverages asynchronous updates and state prioritization to focus computations on high-impact states, such as those near obstacles or goals, ensuring efficient and rapid convergence to an optimal policy for pathfinding.
use ndarray::Array2;
use std::collections::BinaryHeap;
use std::cmp::Ordering;
#[derive(Debug, Clone)]
struct StatePriority {
state: usize,
priority: f64,
}
impl Eq for StatePriority {}
impl PartialEq for StatePriority {
fn eq(&self, other: &Self) -> bool {
self.priority == other.priority
}
}
impl Ord for StatePriority {
fn cmp(&self, other: &Self) -> Ordering {
other.priority.partial_cmp(&self.priority).unwrap()
}
}
impl PartialOrd for StatePriority {
fn partial_cmp(&self, other: &Self) -> Option<Ordering> {
Some(self.cmp(other))
}
}
#[derive(Debug)]
struct GridWorld {
rewards: Array2<f64>,
transitions: Vec<Vec<(usize, f64)>>, // Transition probabilities for state-action pairs
gamma: f64, // Discount factor
grid_size: usize, // Size of the grid (e.g., 4 for a 4x4 grid)
}
impl GridWorld {
/// Create a new grid world with the given size, discount factor, and rewards.
fn new(grid_size: usize, gamma: f64, rewards: Array2<f64>) -> Self {
let transitions = Self::generate_transitions(grid_size);
Self {
rewards,
transitions,
gamma,
grid_size,
}
}
/// Generate transitions for each state-action pair in the grid world.
fn generate_transitions(grid_size: usize) -> Vec<Vec<(usize, f64)>> {
let num_states = grid_size * grid_size;
let mut transitions = Vec::with_capacity(num_states * 4);
for state in 0..num_states {
let (row, col) = (state / grid_size, state % grid_size);
for action in 0..4 {
let mut state_transitions = Vec::new();
match action {
0 => { // UP
if row > 0 {
state_transitions.push((state - grid_size, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
1 => { // DOWN
if row < grid_size - 1 {
state_transitions.push((state + grid_size, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
2 => { // LEFT
if col > 0 {
state_transitions.push((state - 1, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
3 => { // RIGHT
if col < grid_size - 1 {
state_transitions.push((state + 1, 1.0));
} else {
state_transitions.push((state, 1.0)); // Stay in place
}
}
_ => unreachable!(),
}
transitions.push(state_transitions);
}
}
transitions
}
/// Perform prioritized sweeping for value iteration.
fn prioritized_sweeping(&self, theta: f64) -> (Vec<f64>, Vec<usize>) {
let num_states = self.rewards.nrows();
let mut values = vec![0.0; num_states];
let mut policy = vec![0; num_states];
let mut priority_queue = BinaryHeap::new();
for s in 0..num_states {
let residual = self.compute_residual(s, &values);
if residual > theta {
priority_queue.push(StatePriority {
state: s,
priority: residual,
});
}
}
while let Some(StatePriority { state, .. }) = priority_queue.pop() {
let mut best_value = f64::NEG_INFINITY;
let mut best_action = 0;
for action in 0..4 {
let mut action_value = 0.0;
for &(next_state, prob) in &self.transitions[state * 4 + action] {
action_value += prob * (self.rewards[[state, action]] + self.gamma * values[next_state]);
}
if action_value > best_value {
best_value = action_value;
best_action = action;
}
}
let delta = (values[state] - best_value).abs();
values[state] = best_value;
policy[state] = best_action;
if delta > theta {
for &(next_state, _) in &self.transitions[state * 4 + policy[state]] {
let residual = self.compute_residual(next_state, &values);
if residual > theta {
priority_queue.push(StatePriority {
state: next_state,
priority: residual,
});
}
}
}
}
(values, policy)
}
/// Compute the residual for a given state.
fn compute_residual(&self, state: usize, values: &[f64]) -> f64 {
let mut max_residual: f64 = 0.0;
for action in 0..4 {
let mut action_value = 0.0;
for &(next_state, prob) in &self.transitions[state * 4 + action] {
action_value += prob * (self.rewards[[state, action]] + self.gamma * values[next_state]);
}
max_residual = max_residual.max((values[state] - action_value).abs());
}
max_residual
}
/// Print the grid size (example usage of `grid_size`).
fn print_grid_size(&self) {
println!("Grid Size: {}x{}", self.grid_size, self.grid_size);
}
}
fn main() {
let grid_size = 5;
let gamma = 0.9;
let mut rewards = Array2::from_elem((grid_size * grid_size, 4), -1.0);
// Define rewards for goals and obstacles
rewards[[12, 0]] = 10.0; // Goal state (state 12, arbitrary action)
rewards[[6, 0]] = -10.0; // Obstacle (state 6, arbitrary action)
let grid_world = GridWorld::new(grid_size, gamma, rewards);
// Example usage of `grid_size`
grid_world.print_grid_size();
let theta = 0.01;
let (values, policy) = grid_world.prioritized_sweeping(theta);
println!("Value Function: {:?}", values);
println!("Policy: {:?}", policy);
}
The code defines a GridWorld struct with rewards, transitions, discount factor ($\gamma$), and grid size. It initializes the grid world using the new method and dynamically generates transitions for all possible state-action pairs. The prioritized_sweeping function iteratively updates state values using the Bellman equation, focusing on states with the highest residuals (differences between old and new value estimates) stored in a priority queue. Residuals are computed for each state using the compute_residual method. The process continues until residuals fall below a specified threshold ($\theta$), indicating convergence. The final value function and optimal policy are printed, showing the robot's best actions for navigating the grid efficiently while avoiding obstacles and reaching the goal.
By strategically allocating computational resources to the most impactful areas, these methods showcase the power and adaptability of advanced DP techniques in reinforcement learning. This section not only delves into their theoretical underpinnings but also provides readers with actionable insights and practical frameworks to implement these approaches in solving complex, real-world decision-making problems.
4.5. Conclusion
Chapter 4 provides a comprehensive introduction to dynamic programming in reinforcement learning, offering both theoretical insights and practical implementation strategies using Rust. By mastering these concepts, you will gain the ability to solve complex RL problems efficiently, leveraging the power of dynamic programming to find optimal policies and value functions.
4.5.1. Further Learning with GenAI
Engaging with these prompts will help solidify your knowledge and equip you with the skills needed to tackle complex RL problems using dynamic programming techniques.
Explain the principle of dynamic programming and its relevance to reinforcement learning. How does DP help in breaking down complex RL problems into simpler subproblems? Implement a basic DP algorithm in Rust and discuss how it simplifies the problem-solving process.
Discuss the concept of the Bellman equation and its role in dynamic programming. How do the Bellman expectation and Bellman optimality equations relate to policy evaluation and policy optimization? Implement these equations in Rust for a simple RL problem and analyze their behavior.
Analyze the process of policy evaluation in reinforcement learning. How does it work as a fixed-point iteration on the Bellman expectation equation? Implement policy evaluation in Rust and explore how different initialization strategies affect the convergence of the value function.
Examine the policy improvement step in dynamic programming. How does taking greedy actions with respect to the current value function lead to policy improvement? Implement the policy improvement step in Rust and test it on a grid world environment.
Explore the policy iteration algorithm in detail. How does alternating between policy evaluation and policy improvement lead to the discovery of the optimal policy? Implement policy iteration in Rust and visualize the convergence of both the policy and value function over iterations.
Discuss the differences between policy iteration and value iteration. How do these algorithms approach the problem of finding the optimal policy differently? Implement value iteration in Rust and compare its performance with policy iteration in terms of speed and accuracy.
Examine the concept of convergence in dynamic programming. What are the conditions under which DP methods like policy iteration and value iteration are guaranteed to converge to the optimal solution? Implement a Rust-based experiment to test these convergence properties under various scenarios.
Analyze the impact of the discount factor in dynamic programming. How does the choice of discount factor influence the convergence speed and stability of DP algorithms? Implement value iteration in Rust with different discount factors and observe their effects on the value function and policy.
Explore the role of synchronous versus asynchronous updates in dynamic programming. How do these update strategies differ, and what are the advantages and disadvantages of each? Implement both synchronous and asynchronous value iteration in Rust and compare their performance.
Discuss the concept of state prioritization in asynchronous dynamic programming. How can prioritizing certain states over others lead to faster convergence in DP methods? Implement a state-prioritized update schedule in Rust and evaluate its effectiveness in a value iteration algorithm.
Examine the challenges of implementing asynchronous dynamic programming. What are the potential pitfalls, such as sensitivity to update schedules, and how can they be mitigated? Implement a Rust-based asynchronous DP algorithm and experiment with different update strategies to identify best practices.
Discuss the relationship between dynamic programming and other reinforcement learning methods, such as temporal difference (TD) learning. How do DP and TD methods differ in their approach to policy evaluation and optimization? Implement a comparative study in Rust, focusing on the trade-offs between DP and TD methods.
Analyze the computational complexity of dynamic programming algorithms in reinforcement learning. What factors contribute to the computational cost of DP methods, and how can Rust be used to optimize their performance? Implement a Rust-based DP algorithm and experiment with techniques for reducing computational overhead.
Explore the concept of value function approximation in dynamic programming. How can approximation techniques be integrated into DP methods to handle large or continuous state spaces? Implement a value function approximation technique in Rust and test it in a dynamic programming context.
Discuss the importance of modularity and code structure in implementing dynamic programming algorithms in Rust. How can well-structured code improve the maintainability and scalability of DP implementations? Refactor a Rust-based DP implementation to enhance its modularity and test its impact on development efficiency.
Examine the role of Rust’s memory safety features in implementing dynamic programming algorithms. How do Rust’s ownership and borrowing mechanisms help prevent common programming errors in DP implementations? Analyze a Rust-based DP algorithm for memory safety and performance issues.
Explore the concept of backward induction in dynamic programming. How does backward induction differ from forward approaches in solving RL problems, and when is it most effective? Implement backward induction in Rust for a simple RL problem and compare its performance with forward methods.
Discuss the application of dynamic programming in real-world reinforcement learning problems, such as robotics or financial modeling. How can Rust’s performance capabilities be leveraged to implement DP algorithms in these domains? Implement a Rust-based DP solution for a real-world-inspired RL problem and analyze its effectiveness.
Analyze the impact of different stopping criteria on the performance of dynamic programming algorithms. How can the choice of stopping criteria affect the balance between computational cost and solution accuracy? Implement a Rust-based experiment to compare different stopping criteria in a value iteration algorithm.
Explore the potential of parallelizing dynamic programming algorithms in Rust. How can parallel processing be used to speed up the convergence of DP methods? Implement a parallelized DP algorithm in Rust and evaluate its performance in terms of speed and accuracy.
By exploring these robust and comprehensive questions, you will develop a strong technical foundation and gain valuable hands-on experience in implementing and optimizing dynamic programming methods using Rust.
4.5.2. Hands On Practices
Here are five in-depth self-exercises designed to solidify your understanding of dynamic programming (DP) in reinforcement learning and to give you practical experience using Rust.
Exercise 4.1: Implementing Policy Iteration in Rust
Task:
Implement the policy iteration algorithm in Rust for a grid world environment. Start by defining the environment, including states, actions, and rewards.
Use the Bellman expectation equation to evaluate the policy and then improve the policy by making it greedy with respect to the value function.
Challenge:
Experiment with different initialization strategies for the value function and policy. Observe how these strategies impact the convergence speed and final policy.
Implement visualizations in Rust to track the evolution of the value function and policy across iterations.
Exercise 4.2: Comparing Value Iteration and Policy Iteration
Task:
Implement both value iteration and policy iteration algorithms in Rust for the same reinforcement learning problem, such as navigating a simple maze.
Ensure that both implementations are efficient and make use of Rust’s capabilities to handle large state spaces.
Challenge:
Compare the performance of value iteration and policy iteration in terms of computation time, convergence speed, and accuracy of the final policy.
Experiment with different discount factors and stopping criteria to analyze how they affect the performance of each algorithm.
Exercise 4.3: Asynchronous Value Iteration with State Prioritization
Task:
Implement an asynchronous value iteration algorithm in Rust, incorporating state prioritization to update the most "important" states first.
Define a priority function based on the magnitude of value function changes and use it to guide the order of updates.
Challenge:
Compare the performance of the asynchronous method with a standard (synchronous) value iteration algorithm. Analyze how state prioritization impacts convergence speed and computational efficiency.
Experiment with different priority functions and update schedules to optimize the performance of your asynchronous algorithm.
Exercise 4.4: Exploring the Impact of Discount Factors
Task:
Implement a Rust-based simulation of value iteration for a simple MDP, such as a navigation problem with rewards at certain locations.
Run the simulation with various discount factors, ranging from very low (close to 0) to very high (close to 1).
Challenge:
Analyze how the discount factor influences the convergence of the value function and the resulting policy. Focus on how the agent’s behavior changes with different discount factors.
Experiment with different environments and reward structures to see how the optimal discount factor varies with the problem characteristics.
Exercise 4.5: Parallelizing Dynamic Programming in Rust
Task:
Implement a parallelized version of value iteration in Rust, using Rust’s concurrency features such as threads or parallel iterators.
Divide the state space into chunks that can be processed in parallel, ensuring that the value updates remain consistent.
Challenge:
Compare the performance of the parallelized version with a single-threaded implementation in terms of computation time and convergence accuracy.
Experiment with different levels of parallelism and state space partitioning strategies to optimize the speedup and efficiency of your parallelized algorithm.
By implementing these techniques in Rust and experimenting with different parameters and strategies, you will deepen your understanding of the fundamental concepts and learn how to optimize DP algorithms for real-world applications.
Comments