Chapter 10
Model-Based Reinforcement Learning
"Model-based reinforcement learning offers the promise of greater efficiency and robustness by allowing agents to imagine and plan, but it also challenges us to build models that are accurate, scalable, and adaptable." — Pieter Abbeel
Chapter 11 of RLVR delves into the intricacies of Model-Based Reinforcement Learning (MBRL), where the agent constructs a model of the environment to simulate future states and plan actions. The chapter begins by introducing the fundamental concepts of MBRL, emphasizing the importance of the model in approximating the environment’s dynamics and the trade-offs between model-based and model-free approaches. It explores how the agent learns the environment's transition dynamics and reward functions, and how planning algorithms, such as Monte Carlo Tree Search (MCTS), are used to optimize decision-making. The chapter also discusses different model representations, including linear models and neural networks, and their impact on learning accuracy and generalization. Readers will learn to implement and experiment with various planning and control techniques in Rust, integrating them with model-free methods to create robust hybrid approaches. Additionally, the chapter addresses the challenges of MBRL, such as model inaccuracies and computational complexity, and introduces emerging trends like uncertainty-aware models and hierarchical MBRL. Through practical Rust-based implementations and simulations, this chapter equips readers with the knowledge and skills to apply MBRL to complex reinforcement learning tasks, balancing sample efficiency, computational cost, and real-time performance.
10.1. Introduction to Model-Based Reinforcement Learning
The journey through the preceding chapters of RLVR has charted the development of reinforcement learning (RL) from foundational concepts to advanced methodologies. Monte Carlo methods (Chapter 5) established a cornerstone of RL by enabling agents to estimate value functions through episodic returns. These methods illustrated the power of sample-based learning but required complete trajectories for updates, limiting their efficiency in certain contexts. Temporal-Difference (TD) learning (Chapter 6) overcame this limitation by introducing bootstrapping—an approach that allowed incremental updates based on intermediate predictions. This innovation significantly improved computational efficiency and made RL more adaptable to real-time environments.
Function approximation techniques (Chapter 7) further expanded RL’s applicability by allowing algorithms to generalize across large and complex state spaces, addressing the scalability limitations of tabular methods. Eligibility traces (Chapter 8) added another dimension by blending short-term and long-term credit assignment, creating a continuum between TD and Monte Carlo approaches. Finally, policy gradient methods (Chapter 9) brought a paradigm shift by directly optimizing parameterized policies, offering a robust solution for environments with high-dimensional or continuous action spaces. These advancements collectively laid a robust foundation for RL, but they also revealed a fundamental limitation—these methods are predominantly model-free.
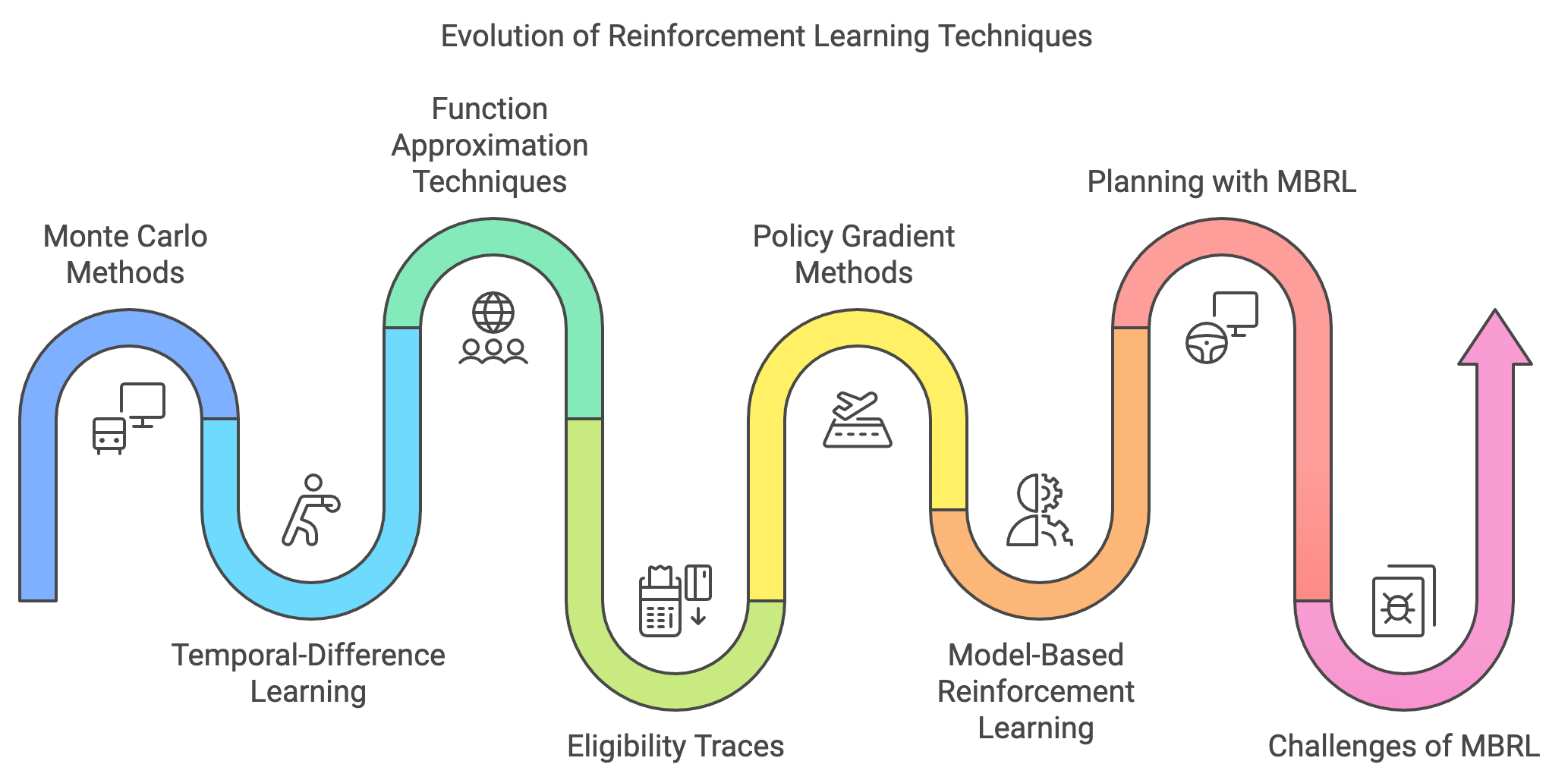
Figure 1: The historical evolution of RL techniques.
Model-free RL algorithms focus on optimizing policies or value functions directly through trial-and-error interactions with the environment. While these methods have demonstrated remarkable success across various domains, including robotics, game-playing, and autonomous systems, their reliance on extensive real-world interactions often makes them sample-inefficient. For example, in a robotic control task, a model-free agent may need thousands of episodes to converge on an optimal policy, potentially causing wear and tear on hardware or incurring significant costs. Moreover, in safety-critical applications like healthcare or autonomous driving, excessive exploration can pose substantial risks, making the inefficiencies of model-free approaches a major bottleneck.
Model-Based Reinforcement Learning (MBRL) represents a paradigm shift aimed at addressing the inefficiencies of model-free methods. Rooted in ideas from both control theory and artificial intelligence, MBRL introduces the concept of constructing an internal model of the environment. This model encapsulates the transition dynamics $P(s'|s, a)$and the reward function $R(s, a)$, enabling the agent to simulate interactions and evaluate potential actions without direct engagement with the environment. By doing so, MBRL achieves superior sample efficiency, minimizing the number of real-world interactions required to learn an effective policy.
The development of MBRL builds on principles introduced in earlier RL methods. For instance, the notion of predicting future states, central to TD learning, aligns with the predictive capabilities of transition models in MBRL. Similarly, the generalization enabled by function approximation techniques is essential for learning accurate models in high-dimensional state spaces. Policy gradient methods also integrate seamlessly into MBRL, often serving as the optimization framework for policies derived from simulated interactions.
The primary advantage of MBRL lies in its ability to leverage the learned model for planning—evaluating future states and actions to inform better decision-making. This capability not only accelerates learning but also reduces the risks associated with real-world exploration. For example, a robot navigating a room with obstacles can construct a virtual representation of the environment, simulating various paths to identify the optimal trajectory. This approach minimizes potential collisions while expediting policy convergence.
However, MBRL is not without challenges. The accuracy of the internal model is critical, as errors in the model can propagate through simulations, leading to suboptimal or even harmful decisions. Balancing computational complexity during planning is another concern, as simulating interactions in high-dimensional environments can be resource-intensive. Additionally, integrating the learned model with policy optimization requires careful tuning to ensure stability and efficiency.
Model-Based RL represents a natural evolution in reinforcement learning, offering a synergy between learning and planning. It complements the model-free techniques discussed in earlier chapters by addressing their inefficiencies while introducing new opportunities for innovation. MBRL’s emphasis on foresight and sample efficiency aligns with the growing demand for RL applications in complex, real-world settings, such as robotics, healthcare, and large-scale simulations.
In the subsequent sections, we will delve deeper into the principles, methodologies, and applications of MBRL. Through examples and detailed discussions, we will explore how MBRL enables agents to navigate the delicate balance between computational efficiency and decision-making accuracy, illustrating its transformative potential in advancing the field of reinforcement learning.
In MBRL, the model is the cornerstone of the learning process. It approximates the environment's dynamics by mapping states and actions to subsequent states and rewards:
$$ s_{t+1} = f(s_t, a_t), \quad r_t = g(s_t, a_t), $$
where $f$ represents the transition dynamics, and $r$ is the reward function. The accuracy of these approximations directly impacts the quality of the agent's decisions.
An analogy to clarify this concept is imagining a chess player. A novice player might rely solely on immediate actions (model-free), while a skilled player mentally simulates potential moves and their consequences (model-based). The accuracy of the mental simulation—the "model"—determines the quality of the player's strategy.
MBRL methods often employ techniques such as linear regression or neural networks to learn the model. Linear models are computationally efficient and interpretable but struggle in complex environments. Neural networks, on the other hand, can capture intricate patterns but require more data and computational resources.
Model-free methods optimize the policy directly, relying solely on interactions with the environment. While simple to implement, they are often sample-inefficient, requiring extensive exploration to learn effective policies. Model-based methods, by contrast, use the learned model to simulate trajectories and evaluate actions without direct interaction. This makes them ideal for tasks where real-world interactions are costly or risky, such as robotic control or autonomous driving.
The trade-offs between these approaches can be summarized mathematically. In a model-free method, the expected return is optimized as:
$$ \pi^* = \arg\max_\pi \mathbb{E}_{\pi} \left[ \sum_{t=0}^\infty \gamma^t R(s_t, a_t) \right]. $$
In a model-based method, the agent optimizes over simulated trajectories:
$$ \pi^* = \arg\max_\pi \mathbb{E}_{f, g} \left[ \sum_{t=0}^\infty \gamma^t R(s_t, a_t) \right], $$
where $f$ and $g$ are the learned dynamics and reward models. This distinction highlights the importance of accurate model learning in MBRL.
Planning is a key component of MBRL, enabling the agent to use the learned model to evaluate potential actions. Algorithms such as Dynamic Programming, Monte Carlo Tree Search (MCTS), and Model Predictive Control (MPC) simulate future trajectories, selecting actions that maximize long-term rewards.
The code below demonstrates an MBRL model applied to a grid world navigation task. In MBRL, the agent leverages a model of the environment's dynamics to plan optimal actions. This code uses Value Iteration, a classical planning algorithm, to compute an optimal policy by iteratively evaluating the value of each state based on the expected rewards and transitions. The environment provides the agent with a reward of 10 for reaching the goal and -0.1 for other transitions, encouraging efficient paths to the goal. By using the learned model, the agent avoids direct trial-and-error exploration, focusing on planning optimal paths.
use ndarray::Array2;
use std::f64;
struct GridWorldEnv {
size: usize,
goal_state: (usize, usize),
}
impl GridWorldEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64, bool) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -0.1 };
let done = next_state == self.goal_state;
(next_state, reward, done)
}
fn reset(&self) -> (usize, usize) {
(0, 0) // Start at top-left corner
}
}
// Value Iteration implementation for Dynamic Programming
// Value Iteration implementation for Dynamic Programming
fn value_iteration(env: &GridWorldEnv, discount_factor: f64, theta: f64) -> (Array2<f64>, Array2<usize>) {
let size = env.size;
let mut value_function = Array2::<f64>::zeros((size, size));
let mut policy = Array2::<usize>::zeros((size, size));
let actions = 4;
loop {
let mut delta: f64 = 0.0;
for row in 0..size {
for col in 0..size {
let state = (row, col);
if state == env.goal_state {
continue;
}
let mut max_value = f64::NEG_INFINITY;
let mut best_action = 0;
for action in 0..actions {
let (next_state, reward, _) = env.step(state, action);
// Ensure next_state is within bounds
if next_state.0 < size && next_state.1 < size {
let value = reward + discount_factor * value_function[[next_state.0, next_state.1]];
if value > max_value {
max_value = value;
best_action = action;
}
}
}
let old_value = value_function[[row, col]];
value_function[[row, col]] = max_value;
policy[[row, col]] = best_action;
delta = delta.max((old_value - max_value).abs());
}
}
if delta < theta {
break;
}
}
(value_function, policy)
}
// Simulate the policy derived from Value Iteration
fn simulate_policy(env: &GridWorldEnv, policy: &Array2<usize>, max_steps: usize) -> f64 {
let mut total_reward = 0.0;
let mut state = env.reset();
for _ in 0..max_steps {
let action = policy[[state.0, state.1]];
let (next_state, reward, done) = env.step(state, action);
total_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward
}
fn main() {
let env = GridWorldEnv {
size: 5,
goal_state: (4, 4),
};
let discount_factor = 0.99;
let theta = 1e-6;
println!("Running Value Iteration...");
let (value_function, policy) = value_iteration(&env, discount_factor, theta);
println!("Value Function:");
for row in 0..env.size {
for col in 0..env.size {
print!("{:6.2} ", value_function[[row, col]]);
}
println!();
}
println!("\nPolicy:");
for row in 0..env.size {
for col in 0..env.size {
print!("{:2} ", policy[[row, col]]);
}
println!();
}
println!("\nSimulating Policy...");
let total_reward = simulate_policy(&env, &policy, 50);
println!("Total Reward: {:.2}", total_reward);
}
The environment model is encapsulated within the GridWorldEnv struct, which defines the state transitions and rewards for all actions. The Value Iteration algorithm serves as the core planning method, iteratively estimating the value of each state by applying the Bellman optimality equation. Using this model, the agent computes the best action for each state to maximize long-term rewards. The optimal policy is stored in a policy array, derived from the value function. This separation of environment modeling and planning exemplifies the MBRL paradigm, where the agent plans actions based on a learned or predefined model rather than relying solely on trial-based policy optimization. After planning, the agent executes the optimal policy, demonstrating how MBRL can enable efficient decision-making in known environments.
This section provides a comprehensive introduction to MBRL, blending theoretical insights with practical Rust implementations. By exploring these concepts, readers gain the tools to build and apply model-based methods to complex reinforcement learning tasks.
10.2. Model Representation and Learning
Model representation is a fundamental aspect of Model-Based Reinforcement Learning (MBRL), defining how the environment’s dynamics and rewards are approximated and stored. The chosen representation influences the agent’s ability to predict transitions and rewards accurately, directly impacting its planning and decision-making capabilities. At its core, model representation seeks to approximate two critical functions: the transition function $f(s, a)$, which predicts the next state $s_{t+1}$, and the reward function $g(s, a)$, which predicts the immediate reward $r_t$:
$$ s_{t+1} = f(s_t, a_t), \quad r_t = g(s_t, a_t). $$
These approximations enable the agent to simulate interactions with the environment, allowing it to plan actions and refine policies without relying solely on real-world experiences. The effectiveness of MBRL hinges on how well these functions represent the underlying dynamics of the environment, particularly in terms of accuracy, scalability, and computational efficiency.
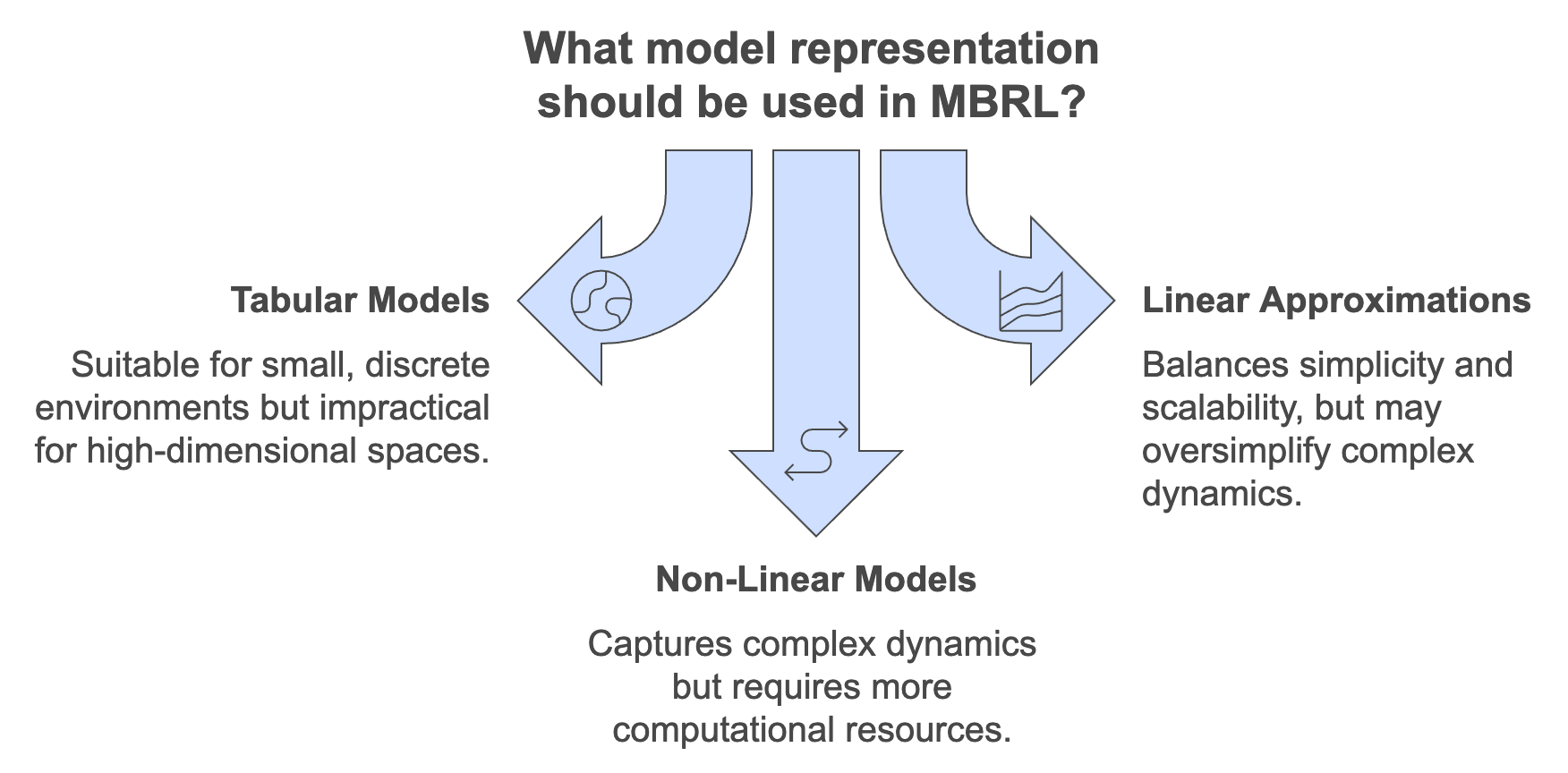
Figure 2: Choices of model representation in MBRL.
The choice of model representation depends on the complexity of the task, the dimensionality of the state-action space, and the available computational resources. Common representations include tabular models, linear approximations, and non-linear models, each with distinct strengths and limitations.
Tabular Models: Tabular representations store exact transitions for each state-action pair, making them suitable for small, discrete environments. For example, in a grid-world task, the transition probabilities and rewards for all possible state-action combinations can be explicitly stored in a lookup table. While this approach ensures high accuracy in capturing environment dynamics, it is computationally infeasible for high-dimensional or continuous spaces due to the exponential growth of state-action pairs. Tabular models also lack generalization, as they treat each state-action pair independently.
Linear Approximations: Linear models assume that the transition and reward functions follow a linear relationship with respect to features derived from states and actions. For instance, the transition function $f(s, a)$ might be expressed as a weighted sum of feature vectors, such as $f(s, a) = \phi(s, a)^T w$, where $\phi(s, a)$ represents the feature vector, and $w$ is the parameter vector. Linear approximations are computationally efficient and require fewer parameters, making them suitable for tasks where state-action dynamics exhibit near-linear behavior. However, their expressiveness is limited, and they struggle to capture complex, non-linear patterns inherent in high-dimensional environments.
Non-Linear Models: Neural networks have become the de facto choice for representing transition and reward functions in complex and high-dimensional environments. These models can approximate non-linear dynamics by learning intricate mappings from states and actions to predicted transitions and rewards. For example, a deep neural network can model the dynamics of a self-driving car navigating a city, capturing intricate road layouts, traffic patterns, and interactions with other vehicles. Neural networks’ ability to generalize across unseen states and actions makes them highly effective in challenging tasks. However, this expressiveness comes at the cost of increased computational complexity, the need for extensive training data, and potential instability during training.
Choosing the appropriate model representation involves a trade-off between expressiveness and computational feasibility. The complexity of the environment and the available data often guide this choice. For simple, discrete environments with well-defined dynamics, tabular or linear models may suffice, offering a balance of simplicity and accuracy. In contrast, tasks involving high-dimensional, continuous states and actions, such as robotic manipulation or autonomous driving, necessitate the use of neural networks or other non-linear models capable of capturing the environment’s intricacies.
For instance, consider a self-driving car navigating a complex urban environment. The car must account for dynamic interactions with pedestrians, other vehicles, and traffic signals, requiring a representation capable of capturing these multi-faceted, non-linear dynamics. A neural network-based model, trained on vast amounts of sensor and simulation data, would be well-suited for this task. On the other hand, a simple grid-world simulation of navigation might only require a tabular or linear model to predict transitions accurately.
Beyond the choice of representation, several advanced considerations impact the effectiveness of model-based RL:
Model Uncertainty: Capturing and quantifying uncertainty in model predictions is critical, especially in high-stakes applications. Techniques such as Bayesian neural networks, Gaussian processes, and ensembles of models can provide confidence intervals for predictions, helping agents make safer and more informed decisions.
Hybrid Representations: In some cases, hybrid approaches combine multiple representations to leverage their respective strengths. For example, linear models might approximate dynamics in regions where transitions are predictable, while neural networks handle regions with complex, non-linear interactions.
Scalability and Parallelization: High-dimensional environments often require scalable training and inference mechanisms. Techniques like distributed training, parallel simulations, and hardware accelerations (e.g., GPUs) are essential for training complex models efficiently.
Transferability: Reusing learned models across similar tasks or environments can significantly improve efficiency. Representations that generalize well across tasks enable agents to adapt quickly, reducing the need for extensive retraining.
Model representation forms the foundation of Model-Based Reinforcement Learning, dictating how effectively an agent can simulate, plan, and optimize its behavior. From tabular models to advanced neural networks, the choice of representation profoundly impacts the scalability, accuracy, and computational efficiency of the agent. As RL applications expand into increasingly complex domains, the ongoing development of robust and adaptable model representations remains a critical area of research, driving the future of model-based RL methodologies.
Model accuracy is pivotal in MBRL because inaccuracies can propagate through planning and result in poor decision-making. For example, if a model consistently predicts incorrect transitions for a critical action, the agent may either avoid that action altogether or overuse it inappropriately, leading to suboptimal or harmful policies. This can be formally understood by considering the error in the predicted transition:
$$ \epsilon(s, a) = \| f(s, a) - s'_{\text{true}} \|, $$
where $s'_{\text{true}}$ is the actual next state. Propagation of these errors during planning accumulates as:
$$ \text{Cumulative Error} = \sum_{t=0}^T \gamma^t \epsilon(s_t, a_t), $$
which distorts the agent's estimation of future returns and undermines its performance.
Uncertainty in model predictions further complicates planning, particularly in stochastic environments. For example, a model predicting multiple possible next states should quantify the uncertainty to ensure robust planning. This is often achieved using probabilistic models or ensemble methods that provide confidence intervals for predictions.
Learning a model involves approximating $f(s, a)$ and $g(s, a)$ from observed transitions. This is typically framed as a supervised learning problem, where the agent collects a dataset of transitions $\{(s_t, a_t, s_{t+1}, r_t)\}$ and trains a model to minimize prediction error:
$$ \mathcal{L} = \frac{1}{N} \sum_{i=1}^N \left( \| f(s_i, a_i) - s_{i+1} \|^2 + \| g(s_i, a_i) - r_i \|^2 \right). $$
For tabular models, this involves directly storing observed transitions. Linear models use regression to fit parameters, while neural networks use gradient-based optimization to minimize the loss. Each approach has its strengths and weaknesses. Tabular models require no assumptions about the environment but scale poorly. Linear models are computationally efficient but fail in non-linear scenarios. Neural networks excel in complex settings but require careful tuning to avoid overfitting.
The following Rust implementation demonstrates how to represent and learn environment dynamics using two models: a simple linear model and a neural network. The code simulates a grid world environment, where an agent starts at the top-left corner and aims to reach the goal at the bottom-right corner. The agent navigates the grid using one of four actions: move up, down, left, or right. Rewards are designed to encourage the agent to reach the goal, with a reward of 10 for success and a penalty of -0.1 for other moves. The primary objective is to compare two models—a simple linear model and a neural network—in learning environment dynamics and aiding the agent in making optimal decisions.
use ndarray::Array2;
use rand::Rng;
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor};
struct GridWorldEnv {
size: usize,
goal_state: (usize, usize),
}
impl GridWorldEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64, bool) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -0.1 };
let done = next_state == self.goal_state;
(next_state, reward, done)
}
fn reset(&self) -> (usize, usize) {
(0, 0) // Start at top-left corner
}
}
fn train_linear_model(env: &GridWorldEnv, episodes: usize) -> (Array2<f64>, Array2<f64>) {
let mut rng = rand::thread_rng();
let mut transitions = Vec::new();
for _ in 0..episodes {
let mut state = env.reset();
for _ in 0..100 {
let action = rng.gen_range(0..4);
let (next_state, reward, _) = env.step(state, action);
transitions.push((state, action, next_state, reward));
state = next_state;
}
}
let total_states = env.size * env.size;
let mut transition_matrix = Array2::<f64>::zeros((total_states, 4));
let mut reward_vector = Array2::<f64>::zeros((total_states, 1));
for (state, action, next_state, reward) in transitions {
let state_index = state.0 * env.size + state.1;
let next_index = next_state.0 * env.size + next_state.1;
if state_index < total_states && action < 4 && next_index < total_states {
transition_matrix[[state_index, action]] = next_index as f64;
reward_vector[[state_index, 0]] = reward;
}
}
(transition_matrix, reward_vector)
}
fn train_neural_model(env: &GridWorldEnv, episodes: usize, device: Device) -> nn::VarStore {
let vs = nn::VarStore::new(device);
let model = nn::seq()
.add(nn::linear(vs.root(), 3, 32, Default::default()))
.add_fn(|x| x.relu())
.add(nn::linear(vs.root(), 32, 3, Default::default()));
let mut optimizer = nn::Adam::default().build(&vs, 1e-3).unwrap();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = env.reset();
for _ in 0..100 {
let action = rng.gen_range(0..4);
let (next_state, reward, _) = env.step(state, action);
// Ensure inputs are `f32`
let state_action_tensor = Tensor::of_slice(&[state.0 as f32, state.1 as f32, action as f32])
.to_device(device)
.unsqueeze(0);
let target_tensor = Tensor::of_slice(&[
next_state.0 as f32,
next_state.1 as f32,
reward as f32,
])
.to_device(device)
.unsqueeze(0);
let prediction = model.forward(&state_action_tensor);
let loss = prediction.mse_loss(&target_tensor, tch::Reduction::Mean);
optimizer.backward_step(&loss);
state = next_state;
}
}
vs
}
fn evaluate_with_linear_model(
env: &GridWorldEnv,
episodes: usize,
horizon: usize,
transition_matrix: &Array2<f64>,
reward_vector: &Array2<f64>,
) -> f64 {
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut cumulative_reward = 0.0;
for _ in 0..horizon {
let state_index = state.0 * env.size + state.1;
let mut best_action = 0;
let mut best_reward = f64::NEG_INFINITY;
for action in 0..4 {
if state_index < transition_matrix.nrows() && action < transition_matrix.ncols() {
let next_index = transition_matrix[[state_index, action]] as usize;
let predicted_reward = if next_index < reward_vector.nrows() {
reward_vector[[next_index, 0]]
} else {
-0.1
};
if predicted_reward > best_reward {
best_action = action;
best_reward = predicted_reward;
}
}
}
let (next_state, reward, done) = env.step(state, best_action);
cumulative_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward += cumulative_reward;
}
total_reward / episodes as f64
}
fn evaluate_with_neural_model(
env: &GridWorldEnv,
episodes: usize,
horizon: usize,
model: &impl nn::Module,
device: Device,
) -> f64 {
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut cumulative_reward = 0.0;
for _ in 0..horizon {
let mut best_action = 0;
let mut best_reward = f64::NEG_INFINITY;
for action in 0..4 {
let state_action_tensor =
Tensor::of_slice(&[state.0 as f32, state.1 as f32, action as f32])
.to_device(device)
.unsqueeze(0);
let prediction = model.forward(&state_action_tensor).detach();
let predicted_reward = prediction.get(0).double_value(&[2]) as f64;
if predicted_reward > best_reward {
best_action = action;
best_reward = predicted_reward;
}
}
let (next_state, reward, done) = env.step(state, best_action);
cumulative_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward += cumulative_reward;
}
total_reward / episodes as f64
}
fn main() {
let env = GridWorldEnv {
size: 5,
goal_state: (4, 4),
};
let episodes = 1000;
let horizon = 20;
let device = Device::cuda_if_available();
println!("Training linear model...");
let (transition_matrix, reward_vector) = train_linear_model(&env, episodes);
println!("Training neural model...");
let neural_model_vs = train_neural_model(&env, episodes, device);
let neural_model = nn::seq()
.add(nn::linear(neural_model_vs.root(), 3, 32, Default::default()))
.add_fn(|x| x.relu())
.add(nn::linear(neural_model_vs.root(), 32, 3, Default::default()));
println!("Evaluating with linear model...");
let linear_reward = evaluate_with_linear_model(&env, 100, horizon, &transition_matrix, &reward_vector);
println!("Evaluating with neural model...");
let neural_reward = evaluate_with_neural_model(&env, 100, horizon, &neural_model, device);
println!("Results:");
println!("Average Reward with Linear Model: {:.2}", linear_reward);
println!("Average Reward with Neural Model: {:.2}", neural_reward);
}
The program begins by simulating random episodes in the environment to collect transition data. This data is used to train two models: a linear model, which represents state transitions and rewards using matrices, and a neural network, which learns these dynamics non-linearly. During evaluation, the models predict outcomes for potential actions, and the agent selects the action with the highest expected reward. The performance of each model is evaluated by calculating the average cumulative reward over multiple episodes, demonstrating their ability to guide the agent toward the goal.
The comparison highlights the trade-offs between the two approaches. The linear model is computationally efficient but may struggle with more complex environments where dynamics are non-linear. The neural network, while capable of capturing these complexities, requires more computational resources and sufficient training data to generalize well. This scenario demonstrates the importance of balancing model complexity and computational efficiency based on the environment's requirements and constraints.
This section provides a detailed exploration of model representation and learning in MBRL, emphasizing the trade-offs between different representations. By combining theoretical insights with practical Rust implementations, readers gain a comprehensive understanding of how to construct and evaluate models for reinforcement learning.
10.3. Planning and Control with Learned Models
Planning in Model-Based Reinforcement Learning (MBRL) is a critical process that differentiates model-based approaches from their model-free counterparts. By leveraging a learned model of the environment’s dynamics, planning enables the agent to simulate future trajectories and optimize its decisions without direct interaction with the real environment. This capability significantly enhances sample efficiency and reduces the risks associated with trial-and-error learning, making planning particularly valuable in domains where interactions are costly, time-consuming, or safety-critical.
The primary objective of planning is to use the transition function $f(s, a)$ and reward function $g(s, a)$, learned by the model, to predict the outcomes of potential actions. This allows the agent to evaluate and compare different action sequences, enabling it to select the one that maximizes long-term rewards. Unlike model-free approaches, which depend entirely on historical interaction data, planning empowers the agent with foresight, allowing it to anticipate the consequences of its actions. For instance, in a robotic arm tasked with assembling a product, planning can simulate various movement trajectories to identify the optimal sequence, avoiding unnecessary wear or the risk of damaging components.
Planning in MBRL is essential for tasks where direct interactions are infeasible or undesirable. Examples include autonomous driving, where physical testing involves high safety risks, and healthcare, where experimentation can have serious ethical implications. In these scenarios, planning enables agents to explore and refine policies within a simulated environment before deployment in the real world.
Several algorithms have been developed to facilitate planning in MBRL, each tailored to different types of tasks and environmental complexities:
Dynamic Programming (DP): Dynamic Programming is one of the earliest and most well-understood planning techniques in reinforcement learning. It relies on the Bellman equation to iteratively compute value functions or policies across the entire state-action space. Algorithms like Value Iteration and Policy Iteration use DP principles to find optimal policies in environments where the model is known or can be learned. While DP provides theoretical guarantees of optimality, its reliance on exhaustive state-space exploration limits its scalability to high-dimensional or continuous spaces. Discussions about DP is covered in Chapter 4 of RLVR.
Model Predictive Control (MPC): MPC is a powerful planning approach widely used in control systems and robotics. It optimizes decisions over a finite time horizon by simulating future trajectories based on the learned model. At each time step, MPC selects the best action sequence, executes the first action, and then re-plans based on updated observations. This iterative re-planning process allows MPC to adapt to dynamic changes in the environment while maintaining computational feasibility. MPC is particularly well-suited for real-time applications, such as self-driving cars and robotic manipulation, where the environment evolves rapidly.
Monte Carlo Tree Search (MCTS): MCTS is a planning algorithm that balances exploration and exploitation by constructing a search tree of possible trajectories. Using Monte Carlo sampling, MCTS evaluates the expected rewards of different branches, prioritizing those that appear most promising. It is especially effective in environments with large action spaces or sparse rewards, such as board games like chess or Go. In MBRL, MCTS leverages the learned model to simulate and expand the search tree, enabling efficient policy improvement through guided exploration.
A key challenge in MBRL is balancing planning with learning. While planning can accelerate policy optimization by simulating interactions, it depends heavily on the accuracy of the learned model. An inaccurate or overly simplistic model can lead to poor planning decisions, as errors in predictions propagate through simulations. Techniques such as model regularization, uncertainty quantification, and model ensembles help address this issue by improving the robustness and reliability of the learned model.
Moreover, planning is computationally intensive, particularly in high-dimensional environments. Algorithms like MPC mitigate this by focusing on a limited time horizon, while MCTS uses heuristics and sampling to guide the search process efficiently. Hybrid approaches that combine model-based planning with model-free learning, such as Dyna-Q and AlphaZero, leverage the strengths of both paradigms. These methods use planning to refine policies in the short term while relying on model-free updates to improve robustness over time.
Monte Carlo Tree Search (MCTS) is a widely used algorithm in decision-making tasks and model-based reinforcement learning (MBRL). It constructs a search tree that evaluates potential actions and their corresponding states, aiming to determine the optimal policy that maximizes long-term rewards. The algorithm operates by iteratively expanding the tree, simulating future trajectories, and using statistical techniques to balance exploration (discovering unvisited or underexplored states) and exploitation (focusing on high-reward regions). The key mathematical concept in MCTS is the evaluation of state-action pairs using the cumulative return:
$$ Q(s, a) = \mathbb{E} \left[ \sum_{t=0}^\infty \gamma^t R(s_t, a_t) \,|\, s_0 = s, a_0 = a \right], $$
where $Q(s, a)$ is the expected cumulative discounted reward, $\gamma \in [0, 1]$ is the discount factor, and $R(s_t, a_t)$ is the immediate reward at time $t$. MCTS builds this evaluation iteratively, focusing on promising trajectories in the search space while approximating $Q(s, a)$ through simulations and backpropagation of values.
The MCTS algorithm is structured into four main steps: selection, expansion, simulation, and backpropagation. In the selection phase, the algorithm starts at the root node (the current state) and navigates down the tree using a policy based on the Upper Confidence Bound (UCB):
$$ UCB(s, a) = Q(s, a) + c \sqrt{\frac{\ln(N(s))}{N(s, a)}}, $$
where $N(s)$ and $N(s, a)$ denote the visit counts of state $s$ and action $a$, respectively, and $c$ is a constant that controls the exploration-exploitation tradeoff. The UCB formula prioritizes actions with high $Q(s, a)$ or low visitation counts, balancing the search. Once a leaf node is reached (a state with unvisited actions), the expansion phase begins, and a new child node (state) is added to the tree corresponding to an untried action.
In the simulation phase, a rollout policy, typically random, is used to simulate a trajectory from the newly expanded node. The simulation accumulates rewards along the trajectory, providing an estimate of the return. This estimate is then backpropagated up the tree to update the $Q(s, a)$ values and visit counts for all nodes and edges traversed during the selection phase. The updated$Q(s, a)$ is computed as a running average of the returns obtained from all simulations passing through the state-action pair. The pseudo-code for MCTS is as follows:
def mcts(root, model, iterations, gamma, exploration_constant):
"""
Perform MCTS to find the best action from the root state.
Args:
root: Initial state (root node of the tree).
model: Transition and reward model for simulations.
iterations: Number of MCTS iterations.
gamma: Discount factor for rewards.
exploration_constant: Constant for UCB to balance exploration and exploitation.
Returns:
Best action determined by MCTS.
"""
tree = initialize_tree(root) # Initialize tree with root node
for _ in range(iterations):
# Selection
node = root
path = []
while node.is_fully_expanded():
action = select_action(node, exploration_constant) # Use UCB
path.append((node, action))
node = node.children[action]
# Expansion
if not node.is_terminal():
new_node = node.expand() # Add a new child node for an unvisited action
path.append((node, new_node.action))
node = new_node
# Simulation
reward = simulate(node, model, gamma) # Rollout a trajectory from the expanded node
# Backpropagation
for parent, action in reversed(path):
parent.update(action, reward) # Update Q(s, a) and visit counts
reward *= gamma # Apply discount factor
# Return the best action from the root
return root.get_best_action()
In the above pseudo-code, the select_action function calculates UCB for all available actions at a node and selects the one with the highest value. The simulate function performs a rollout using the model and a simple policy, estimating the cumulative reward for a trajectory. The backpropagation step ensures that information from the simulated trajectory updates the nodes along the path to the root.
Mathematically, during backpropagation, for a visited node $s_i$ and action $a_i$, the cumulative reward $Q(s_i, a_i)$ is updated as:
$$Q(s_i, a_i) \leftarrow \frac{N(s_i, a_i) \cdot Q(s_i, a_i) + R_{sim}}{N(s_i, a_i) + 1},$$
where $R_{sim}$ is the simulated reward, and $N(s_i, a_i)$ is incremented to account for the new visit. This recursive update allows the tree to refine its estimates of $Q(s, a)$ as more simulations are performed.
MCTS is particularly effective in large or continuous state-action spaces because it focuses its computations on the most promising regions of the tree. By incorporating exploration-exploitation strategies through UCB and leveraging the power of simulations, MCTS efficiently guides the agent toward actions that maximize long-term rewards. The algorithm's performance can be further enhanced by integrating domain-specific knowledge into the rollout policy or leveraging learned models for better simulations.
However, there are trade-offs between model accuracy and computational complexity. Highly accurate models improve planning quality but require significant resources to construct and simulate. Conversely, simpler models may lead to faster planning but risk suboptimal decisions due to inaccuracies.
Model Predictive Control (MPC) is an optimization-based planning algorithm used extensively in Model-Based Reinforcement Learning (MBRL) and control systems. Unlike Monte Carlo Tree Search (MCTS), MPC solves a sequence of optimization problems to determine the best action by simulating future trajectories over a fixed planning horizon. It aims to maximize the expected cumulative reward by leveraging a learned or known model of the environment. At each timestep, MPC computes an optimal sequence of actions but only executes the first action, repeating the process at subsequent timesteps to adapt to updated state information. The core mathematical formulation of MPC is based on the maximization of the cumulative discounted reward:
$$ \max_{\{a_t\}_{t=0}^{H-1}} \sum_{t=0}^{H-1} \gamma^t R(s_t, a_t), $$
subject to the constraints given by the model dynamics: $s_{t+1} = f(s_t, a_t), \quad a_t \in \mathcal{A}, \quad s_t \in \mathcal{S}$.
Here, $H$ is the planning horizon, $\gamma \in [0, 1]$ is the discount factor, $R(s_t, a_t)$ is the reward function, $f(s_t, a_t)$ is the learned or predefined transition model, $\mathcal{A}$ is the action space, and $\mathcal{S}$ is the state space. The algorithm iteratively optimizes the sequence of actions, predicts the resulting states, and evaluates the rewards over the horizon $H$.
MPC proceeds in three main phases: trajectory optimization, action execution, and model update. In trajectory optimization, the algorithm uses the model $f(s_t, a_t)$ to simulate state transitions and optimize the sequence of actions $\{a_t\}_{t=0}^{H-1}$ that maximize the cumulative reward. This optimization is often performed using gradient-based methods, sampling-based approaches, or derivative-free optimization techniques. After determining the optimal action sequence, MPC executes only the first action a0a_0a0, observes the resulting next state $s_1$, and then updates the optimization based on the new state. The pseudo-code for MPC is as follows:
def mpc(state, model, horizon, gamma, optimizer, reward_fn):
"""
Perform Model Predictive Control (MPC) to determine the best action.
Args:
state: Current state of the environment.
model: Transition model for state predictions.
horizon: Planning horizon.
gamma: Discount factor for future rewards.
optimizer: Optimization method (e.g., gradient-based or sampling-based).
reward_fn: Function to compute rewards.
Returns:
Optimal action to execute.
"""
# Initialize action sequence
actions = initialize_action_sequence(horizon)
def objective(actions):
cumulative_reward = 0.0
current_state = state
discount = 1.0
for t in range(horizon):
cumulative_reward += discount * reward_fn(current_state, actions[t])
current_state = model(current_state, actions[t]) # Predict next state
discount *= gamma
return -cumulative_reward # Negative because we minimize in optimization
# Optimize the action sequence
optimal_actions = optimizer(objective, actions)
# Return the first action
return optimal_actions[0]
In the pseudo-code, the objective function calculates the negative cumulative reward for the given action sequence, as optimization algorithms typically minimize the objective. The optimizer updates the action sequence to maximize the reward over the planning horizon. After optimization, the algorithm executes only the first action, ensuring that MPC remains adaptable to updated state information.
MPC relies heavily on the accuracy of the model $f(s_t, a_t)$, which may be a learned neural network or a physics-based simulator. Mathematically, at each timestep, the optimal action sequence is computed as:
$$ \{a_t^*\}_{t=0}^{H-1} = \arg\max_{\{a_t\}} \sum_{t=0}^{H-1} \gamma^t R(s_t, a_t), $$
where the states $s_{t+1}$ are recursively computed using the model $f(s_t, a_t)$.
MPC is particularly effective in handling constraints on the state and action spaces, as these can be explicitly incorporated into the optimization problem. For instance, constraints such as $a_t \in [a_{\text{min}}, a_{\text{max}}]$ or $s_t \in [s_{\text{min}}, s_{\text{max}}]$ can be directly included in the trajectory optimization process. Additionally, MPC's receding horizon nature ensures that the algorithm continuously adapts to changes in the environment or model inaccuracies.
One of MPC's strengths is its ability to balance exploration and exploitation by simulating multiple trajectories and selecting the one with the highest reward. However, it can be computationally expensive, particularly in high-dimensional action spaces or when the model dynamics are complex. To address this, sampling-based approaches like Cross-Entropy Method (CEM) or differentiable models with gradient optimization are often employed to improve computational efficiency.
In summary, MPC uses a combination of optimization and model-based simulation to determine the best action at each timestep, maximizing long-term rewards while remaining adaptable to new information. Its robustness in constrained settings and ability to handle dynamic environments make it a powerful tool in MBRL and control applications.
The following example demonstrates the implementation of a basic model-based reinforcement learning algorithm in Rust. In this code, we compare two RL-inspired approaches—Monte Carlo Tree Search (MCTS) and Model Predictive Control (MPC)—in navigating a simple grid world. MCTS uses random simulations to evaluate potential moves, while MPC relies on a learned model of the environment to predict and optimize actions.
use ndarray::Array2;
use rand::Rng;
struct GridWorldEnv {
size: usize,
goal_state: (usize, usize),
}
impl GridWorldEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64, bool) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -0.1 };
let done = next_state == self.goal_state;
(next_state, reward, done)
}
fn reset(&self) -> (usize, usize) {
(0, 0) // Start at top-left corner
}
}
fn mcts(env: &GridWorldEnv, episodes: usize, rollout_depth: usize) -> f64 {
let mut rng = rand::thread_rng();
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut cumulative_reward = 0.0;
for _ in 0..rollout_depth {
let action = rng.gen_range(0..4); // Random action
let (next_state, reward, done) = env.step(state, action);
cumulative_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward += cumulative_reward;
}
total_reward / episodes as f64
}
fn mpc(
env: &GridWorldEnv,
episodes: usize,
horizon: usize,
transition_matrix: &Array2<f64>,
reward_vector: &Array2<f64>,
) -> f64 {
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut cumulative_reward = 0.0;
for _ in 0..horizon {
let state_index = state.0 * env.size + state.1;
let mut best_action = 0;
let mut best_reward = f64::NEG_INFINITY;
for action in 0..4 {
if state_index < transition_matrix.nrows() && action < transition_matrix.ncols() {
let next_index = transition_matrix[[state_index, action]] as usize;
let predicted_reward = if next_index < reward_vector.nrows() {
reward_vector[[next_index, 0]]
} else {
-0.1
};
if predicted_reward > best_reward {
best_action = action;
best_reward = predicted_reward;
}
}
}
let (next_state, reward, done) = env.step(state, best_action);
cumulative_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward += cumulative_reward;
}
total_reward / episodes as f64
}
fn train_model(env: &GridWorldEnv, episodes: usize) -> (Array2<f64>, Array2<f64>) {
let mut rng = rand::thread_rng();
let mut transitions = Vec::new();
for _ in 0..episodes {
let mut state = env.reset();
for _ in 0..100 {
let action = rng.gen_range(0..4);
let (next_state, reward, _) = env.step(state, action);
transitions.push((state, action, next_state, reward));
state = next_state;
}
}
let total_states = env.size * env.size;
let mut transition_matrix = Array2::<f64>::zeros((total_states, 4));
let mut reward_vector = Array2::<f64>::zeros((total_states, 1));
for (state, action, next_state, reward) in transitions {
let state_index = state.0 * env.size + state.1;
let next_index = next_state.0 * env.size + next_state.1;
if state_index < total_states && action < 4 && next_index < total_states {
transition_matrix[[state_index, action]] = next_index as f64;
reward_vector[[state_index, 0]] = reward;
}
}
(transition_matrix, reward_vector)
}
fn main() {
let env = GridWorldEnv {
size: 5,
goal_state: (4, 4),
};
let episodes = 100;
let rollout_depth = 20;
let horizon = 20;
println!("Training model for MPC...");
let (transition_matrix, reward_vector) = train_model(&env, 1000);
println!("Running MCTS...");
let mcts_reward = mcts(&env, episodes, rollout_depth);
println!("Running MPC...");
let mpc_reward = mpc(&env, episodes, horizon, &transition_matrix, &reward_vector);
println!("Results:");
println!("MCTS Average Reward: {:.2}", mcts_reward);
println!("MPC Average Reward: {:.2}", mpc_reward);
}
The GridWorldEnv represents a 5x5 grid where the agent starts at the top-left corner and aims to reach the goal at the bottom-right corner. The mcts function simulates episodes by selecting random actions, evaluating their rewards, and averaging results over multiple rollouts. The mpc function uses a transition matrix and reward vector learned from the environment (via the train_model function) to choose the best predicted action at each step. The main function initializes the environment, trains the model for MPC, runs both approaches for evaluation, and outputs their average rewards.
The results demonstrate the effectiveness of each approach in this controlled grid-world scenario. MCTS, which relies solely on random rollouts, provides a baseline but lacks precision in environments with sparse rewards. MPC, leveraging its learned model, is generally more efficient and achieves higher average rewards by predicting outcomes and selecting optimal actions. The comparison highlights the trade-offs between model-free methods like MCTS and model-based approaches like MPC in solving RL tasks.
Recent advancements in MBRL have introduced novel approaches to planning that extend its applicability to complex, real-world scenarios:
Latent-Space Planning: Instead of planning directly in the raw state space, some methods use latent representations learned by neural networks to reduce dimensionality and focus on relevant features. This approach is particularly useful in high-dimensional environments like vision-based tasks.
Uncertainty-Aware Planning: Incorporating uncertainty estimates into the planning process helps the agent account for model inaccuracies and explore areas with high uncertainty. Bayesian neural networks, Gaussian processes, and ensemble models are commonly used for this purpose.
Hierarchical Planning: In complex tasks, hierarchical approaches decompose planning into high-level and low-level decisions. For example, a robot might plan a high-level path through a building and then use a detailed planner for navigating individual rooms.
Planning is the cornerstone of Model-Based Reinforcement Learning, offering a distinct advantage over model-free methods by enabling agents to anticipate and optimize their actions through simulation. Common algorithms like Dynamic Programming, Model Predictive Control, and Monte Carlo Tree Search provide robust frameworks for leveraging learned models in diverse applications. As MBRL continues to evolve, advancements in planning techniques, coupled with innovations in model representation and uncertainty handling, promise to expand its impact across a wide range of domains, from robotics and healthcare to autonomous systems and artificial intelligence research.
The primary advantage of planning lies in its ability to simulate outcomes and refine decisions before acting in the real environment. For instance, an agent controlling a robotic arm can simulate various trajectories using the model and select the one that avoids obstacles while maximizing efficiency. Planning algorithms like MPC optimize decisions over a finite horizon, ensuring real-time applicability, while MCTS explores possible action sequences to identify optimal strategies.
Control in MBRL refers to translating these planned decisions into executable actions. The integration of planning and control ensures that the agent not only formulates optimal strategies but also implements them effectively, adapting to changes in the environment.
Planning depth, defined as the number of simulated steps into the future, directly influences decision quality and computational cost. Deeper planning typically results in more informed decisions but increases the risk of compounding model errors and demands higher computational resources. This trade-off is formalized as:
$$ \text{Planning Error} = \sum_{t=0}^d \gamma^t \epsilon(s_t, a_t), $$
where $d$ is the planning depth, and $\epsilon(s_t, a_t)$ represents the model error. While shallow planning is computationally efficient, it may overlook long-term consequences, making deeper planning essential for complex tasks.
The following code explores MBRL approaches for solving a grid world navigation problem. The agent starts at the top-left corner of a grid and aims to reach the goal state at the bottom-right corner while maximizing cumulative rewards. Three planning strategies are implemented: Latent-Space Planning, which simplifies decision-making by operating in a reduced state space; Uncertainty-Aware Planning, which incorporates probabilistic modeling of rewards and transitions; and Hierarchical Planning, which divides the problem into high-level and low-level planning for efficient navigation.
use ndarray::{Array3};
use rand::Rng;
use std::f64;
/// Environment structure representing the grid world
struct GridWorldEnv {
size: usize,
goal_state: (usize, usize),
}
impl GridWorldEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64, bool) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -0.1 };
let done = next_state == self.goal_state;
(next_state, reward, done)
}
fn reset(&self) -> (usize, usize) {
(0, 0) // Start at top-left corner
}
}
/// Latent-Space Planning using a simplified representation
fn latent_space_planning(env: &GridWorldEnv, episodes: usize) -> f64 {
let mut rng = rand::thread_rng();
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut cumulative_reward = 0.0;
for _ in 0..100 {
// Plan actions based on a simple latent encoding
let latent_state = (state.0 as f64 / env.size as f64, state.1 as f64 / env.size as f64);
let action = if latent_state.0 < 0.5 {
1 // Move down if "closer to the top"
} else if latent_state.1 < 0.5 {
3 // Move right if "closer to the left"
} else {
rng.gen_range(0..4) // Random fallback
};
let (next_state, reward, done) = env.step(state, action);
cumulative_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward += cumulative_reward;
}
total_reward / episodes as f64
}
/// Uncertainty-Aware Planning: Include variance in reward modeling
fn uncertainty_aware_planning(env: &GridWorldEnv, episodes: usize) -> f64 {
let mut rng = rand::thread_rng();
let mut total_reward = 0.0;
let mut reward_model = Array3::<f64>::zeros((env.size, env.size, 4)); // Mean reward model
let mut reward_variance = Array3::<f64>::zeros((env.size, env.size, 4)); // Uncertainty model
// Collect transition data
for _ in 0..episodes {
let mut state = env.reset();
for _ in 0..100 {
let action = rng.gen_range(0..4);
let (next_state, reward, _) = env.step(state, action);
if state.0 < env.size && state.1 < env.size && action < 4 {
// Update mean and variance for this state-action pair
reward_model[[state.0, state.1, action]] += reward;
reward_variance[[state.0, state.1, action]] += reward.powi(2);
}
state = next_state;
}
}
// Compute mean and variance
for ((row, col, act), value) in reward_model.indexed_iter_mut() {
*value /= episodes as f64;
reward_variance[[row, col, act]] = (reward_variance[[row, col, act]] / episodes as f64) - value.powi(2);
}
// Plan considering uncertainty
for _ in 0..episodes {
let mut state = env.reset();
let mut cumulative_reward = 0.0;
for _ in 0..100 {
let mut best_action = 0;
let mut best_score = f64::NEG_INFINITY;
for action in 0..4 {
if state.0 < env.size && state.1 < env.size && action < 4 {
let mean = reward_model[[state.0, state.1, action]];
let variance = reward_variance[[state.0, state.1, action]];
let score = mean + 0.5 * variance.sqrt(); // Balance reward and uncertainty
if score > best_score {
best_score = score;
best_action = action;
}
}
}
let (next_state, reward, done) = env.step(state, best_action);
cumulative_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward += cumulative_reward;
}
total_reward / episodes as f64
}
/// Hierarchical Planning: Use high-level and low-level planning
fn hierarchical_planning(env: &GridWorldEnv, high_level_grid_size: usize, episodes: usize) -> f64 {
let high_level_factor = env.size / high_level_grid_size;
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut cumulative_reward = 0.0;
while state != env.goal_state {
// High-level planning
let high_level_state = (state.0 / high_level_factor, state.1 / high_level_factor);
let high_level_goal = (env.goal_state.0 / high_level_factor, env.goal_state.1 / high_level_factor);
let action = if high_level_state.0 < high_level_goal.0 {
1 // Move down
} else if high_level_state.1 < high_level_goal.1 {
3 // Move right
} else {
0 // Default to up
};
// Low-level planning (execute high-level action multiple steps)
for _ in 0..high_level_factor {
let (next_state, reward, done) = env.step(state, action);
cumulative_reward += reward;
if done {
state = next_state;
break;
}
state = next_state;
}
}
total_reward += cumulative_reward;
}
total_reward / episodes as f64
}
fn main() {
let env = GridWorldEnv {
size: 5,
goal_state: (4, 4),
};
println!("Latent-Space Planning...");
let latent_reward = latent_space_planning(&env, 100);
println!("Latent-Space Planning Average Reward: {:.2}", latent_reward);
println!("Uncertainty-Aware Planning...");
let uncertainty_reward = uncertainty_aware_planning(&env, 100);
println!("Uncertainty-Aware Planning Average Reward: {:.2}", uncertainty_reward);
println!("Hierarchical Planning...");
let hierarchical_reward = hierarchical_planning(&env, 2, 100);
println!("Hierarchical Planning Average Reward: {:.2}", hierarchical_reward);
}
The environment is modeled as a grid where the agent selects one of four actions: move up, down, left, or right. For Latent-Space Planning, states are mapped to a reduced representation, and the agent plans based on coarse characteristics. Uncertainty-Aware Planning builds models of mean rewards and variances for state-action pairs to balance exploration and exploitation. Hierarchical Planning divides the grid into high-level regions, using coarse planning to determine subgoals, and fine planning to navigate within each region. Each method computes a policy guiding the agent toward the goal and evaluates its effectiveness by simulating multiple episodes and averaging rewards.
The three approaches demonstrate distinct trade-offs. Latent-Space Planning is computationally efficient but may sacrifice accuracy due to the coarse nature of the latent representation. Uncertainty-Aware Planning balances risk and reward by considering uncertainty, which can lead to more robust decisions but requires more computational resources for probabilistic modeling. Hierarchical Planning excels in scalability by simplifying high-level decision-making and refining actions at a lower level, making it effective for larger or complex environments. Overall, the choice of strategy depends on the specific problem, computational constraints, and desired balance between efficiency and precision.
As summary of this section, planning and control are central to MBRL, enabling agents to leverage learned models for robust decision-making. By implementing planning algorithms like MCTS in Rust, practitioners can explore the trade-offs between planning depth and computational cost while understanding the critical role of accuracy in learned models. This section provides a foundation for integrating planning into complex reinforcement learning pipelines.
10.4. Combining Model-Based and Model-Free Approaches
Hybrid approaches in reinforcement learning (RL) represent an advanced strategy that combines the strengths of model-based and model-free methods to overcome the limitations of each individual paradigm. Model-free methods, such as policy gradient algorithms, excel in adaptability and robustness but suffer from high sample inefficiency, requiring extensive real-world interactions. In contrast, model-based methods leverage predictive models of the environment to plan and simulate actions, offering significant sample efficiency. However, they are prone to inaccuracies in learned models, which can lead to suboptimal decisions. By merging these paradigms, hybrid approaches create a framework that capitalizes on the sample efficiency of model-based rollouts while retaining the adaptability and resilience of model-free policies.
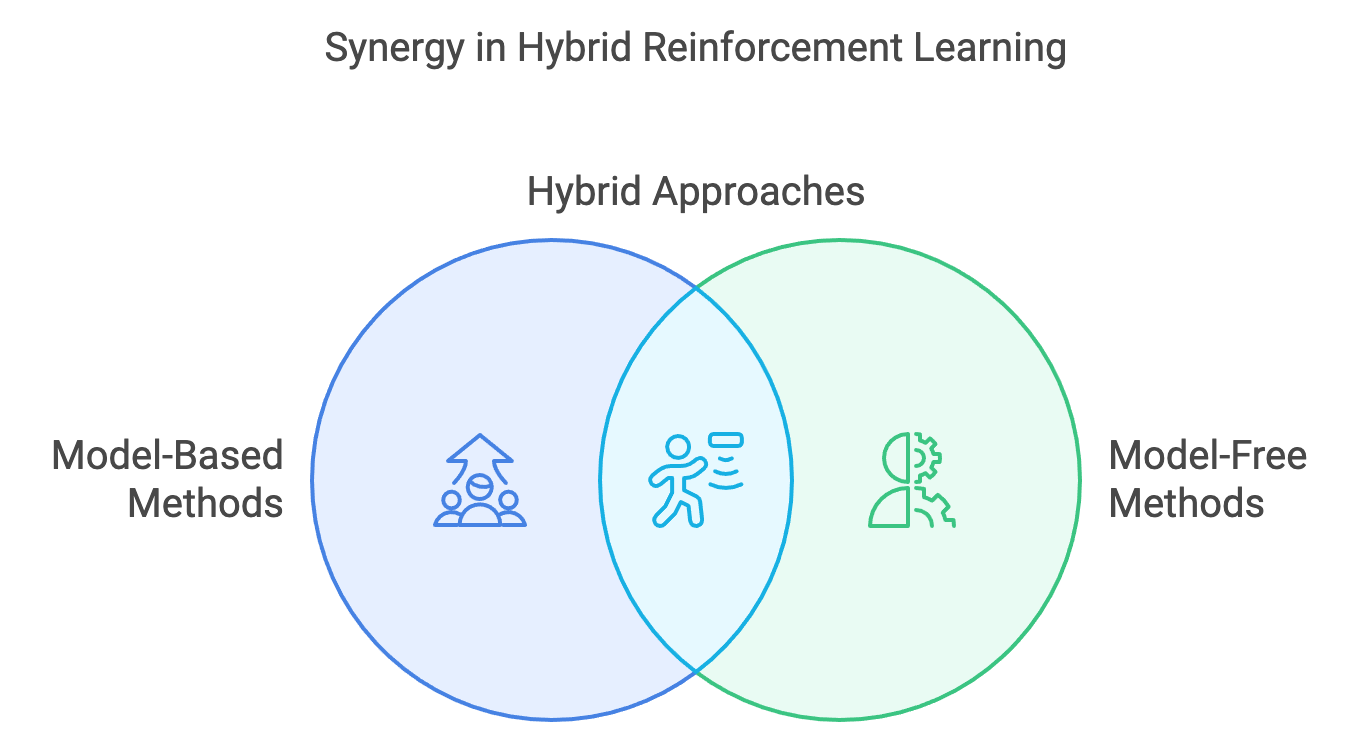
Figure 3: Hybrid Reinforcement Learning model.
The core mechanism underpinning hybrid RL approaches is the concept of rollouts: simulated trajectories generated using a learned model of the environment’s dynamics. These rollouts allow the agent to predict future transitions and rewards, augmenting the training data used in model-free learning. By integrating simulated experiences with real-world data, the agent reduces its dependence on costly or risky real-world interactions. For instance, an agent navigating a maze can use its learned model to simulate multiple potential paths, refining its policy without physically exploring every option.
Mathematically, hybrid approaches often integrate the gradients of model-based and model-free objectives. A typical formulation combines these components as follows:
$$ \Delta \theta = \alpha \nabla_\theta \mathbb{E}_{s, a \sim \pi_\theta} [R(s, a)] + \beta \nabla_\theta \mathbb{E}_{s', r \sim f} [R(s', a)], $$
where:
$\pi_\theta$ is the policy parameterized by θ\\thetaθ,
$f$ represents the learned model of the environment,
$R(s, a)$ is the reward function,
$\alpha$ and $\beta$ are coefficients controlling the contributions of the model-free and model-based components.
This formulation allows hybrid methods to balance the reliability of model-free learning with the efficiency of model-based planning, ensuring that the policy adapts robustly even when the learned model is imperfect. Hybrid RL approaches are implemented using various strategies, each tailored to leverage the strengths of both paradigms:
Dyna Architecture: Introduced by Sutton, the Dyna framework integrates model-free RL with a model-based component that generates synthetic experiences. In this approach, the agent learns a model of the environment and uses it to simulate transitions, which are then used to update the value function or policy. This hybrid architecture has been successfully applied in tasks where real-world interactions are limited, demonstrating significant improvements in sample efficiency.
Integrated Model-Free and Model-Based Policies: Some hybrid methods train separate model-free and model-based components and combine their outputs during decision-making. For example, the model-based component may suggest candidate actions based on simulated rollouts, while the model-free component provides a more refined evaluation of these actions using empirical data. This division of labor ensures that the agent benefits from the foresight of model-based planning without becoming overly reliant on potentially inaccurate models.
Guided Exploration: Hybrid approaches can guide exploration by leveraging model-based predictions to focus the agent's interactions on promising regions of the state-action space. For instance, an agent might use model-based rollouts to identify areas where the reward gradient is steep, directing its real-world exploration to regions likely to yield significant policy improvements.
Ensemble Models for Robustness: To mitigate the impact of model inaccuracies, hybrid methods often use ensemble models to estimate dynamics. By aggregating predictions from multiple models, the agent can quantify uncertainty and adjust its reliance on model-based rollouts accordingly. This approach enhances the robustness of hybrid methods, particularly in stochastic or complex environments.
The effectiveness of hybrid RL methods hinges on the careful balance between model-free and model-based contributions. Excessive reliance on model-based rollouts can lead to overfitting to the learned model, particularly if the model is inaccurate or poorly generalized. Conversely, underutilizing model-based components may squander opportunities for improving sample efficiency. Coefficients $\alpha$ and $\beta$ in the gradient formulation play a crucial role in tuning this balance, allowing the agent to dynamically adapt its learning strategy based on the quality of the learned model and the nature of the environment.
Advanced techniques such as uncertainty-aware hybrid RL further enhance this balance. By quantifying the uncertainty of model predictions, agents can adjust their reliance on simulated rollouts, emphasizing model-free updates when uncertainty is high. This dynamic adjustment ensures that hybrid approaches remain robust across a wide range of tasks and environments.
Hybrid reinforcement learning methods are particularly well-suited for environments where interactions are expensive or risky but require policies that generalize effectively to complex scenarios. For instance:
Robotics: Hybrid methods enable robots to simulate and refine their actions in virtual environments before deployment, reducing wear and tear on hardware and improving operational safety.
Autonomous Vehicles: By combining real-world driving data with simulated rollouts, hybrid approaches can optimize driving policies with fewer real-world trials.
Healthcare: Hybrid RL can simulate treatment plans based on patient models, augmenting limited clinical data with synthetic experiences to improve decision-making.
While hybrid approaches offer significant advantages, they also present challenges. The accuracy of the learned model remains a critical factor, as errors in the model can propagate through rollouts and degrade policy performance. Additionally, computational complexity can increase due to the dual reliance on model-based and model-free components. Future advancements are likely to focus on improving model accuracy through advanced representation learning, reducing computational overhead with more efficient algorithms, and enhancing adaptability in hybrid frameworks through techniques like meta-learning.
In conclusion, hybrid reinforcement learning methods represent a powerful synergy of model-based and model-free approaches, offering a balanced framework that addresses the limitations of each paradigm. By leveraging the predictive capabilities of learned models while maintaining the adaptability of empirical learning, hybrid methods provide a robust foundation for tackling complex, real-world challenges across diverse domains.
Model-based rollouts enable the agent to "imagine" future scenarios by simulating transitions and rewards using the learned model. These simulations not only enhance sample efficiency but also allow the agent to explore rare or risky scenarios in a safe, controlled manner. For instance, an autonomous vehicle can use rollouts to evaluate potential collision risks under various conditions, refining its policy without endangering passengers.
Imagination plays a crucial role in hybrid RL, where the agent leverages its model to evaluate hypothetical trajectories. This process involves simulating sequences of actions and rewards to estimate the value of different policies:
$$ \hat{Q}(s, a) = R(s, a) + \gamma \mathbb{E}_{s' \sim f(s, a)} \left[ \max_{a'} \hat{Q}(s', a') \right]. $$
These imagined experiences supplement real-world data, accelerating learning and enabling the agent to generalize better across states.
A critical challenge in hybrid approaches is deciding when to rely on the model and when to trust empirical data. While models offer the advantage of foresight, inaccuracies can lead to suboptimal decisions or policy divergence. This balance is often achieved through uncertainty estimation, where the agent assesses the confidence of its model predictions. For example, if the model is uncertain about a specific state-action transition, the agent prioritizes direct interaction with the environment to gather accurate data.
Hybrid approaches also help navigate the exploration-exploitation dilemma by integrating model-based planning with model-free adaptability. The model-based component enables efficient exploration through targeted rollouts, while the model-free component refines the policy based on observed rewards, ensuring robust decision-making.
The code implements a Hybrid RL framework for a grid world navigation task. The agent starts at the top-left corner of a 5x5 grid and aims to reach the bottom-right goal state while maximizing cumulative rewards. The hybrid approach combines model-free reinforcement learning (directly updating policies based on observed rewards) and model-based planning (using a learned model of the environment for simulated rollouts). This integration enables the agent to balance real-world exploration with imagined rollouts for more efficient learning.
use ndarray::Array2;
use rand::Rng;
struct GridWorldEnv {
size: usize,
goal_state: (usize, usize),
}
impl GridWorldEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64, bool) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -0.1 };
let done = next_state == self.goal_state;
(next_state, reward, done)
}
fn reset(&self) -> (usize, usize) {
(0, 0) // Start at top-left corner
}
}
struct HybridRL {
policy: Array2<f64>,
model: Array2<f64>, // Learned model: transition probabilities
alpha: f64, // Model-free learning rate
beta: f64, // Model-based rollout weight
}
impl HybridRL {
fn new(size: usize) -> Self {
HybridRL {
policy: Array2::ones((size * size, 4)), // Initialize policy uniformly
model: Array2::zeros((size * size, 4)), // Initialize empty model
alpha: 0.01,
beta: 0.1,
}
}
fn update_model(&mut self, state: usize, action: usize, next_state: usize) {
if state < self.model.nrows() && action < self.model.ncols() {
self.model[[state, action]] = next_state as f64;
}
}
fn rollout(&self, state: usize) -> f64 {
let mut rng = rand::thread_rng();
let mut current_state = state;
let mut total_reward = 0.0;
let mut discount = 1.0;
for _ in 0..10 {
let action = rng.gen_range(0..4);
if current_state < self.model.nrows() && action < self.model.ncols() {
let next_state = self.model[[current_state, action]] as usize;
total_reward += discount * (-0.1); // Reward for each step
discount *= 0.9;
current_state = next_state;
}
}
total_reward
}
fn update_policy(&mut self, state: usize, action: usize, reward: f64) {
if state < self.policy.nrows() && action < self.policy.ncols() {
self.policy[[state, action]] += self.alpha * reward;
}
}
}
fn main() {
let env = GridWorldEnv {
size: 5,
goal_state: (4, 4),
};
let mut agent = HybridRL::new(env.size);
for _ in 0..1000 {
let mut state = env.reset();
loop {
let action = rand::thread_rng().gen_range(0..4);
let (next_state, reward, done) = env.step(state, action);
let state_index = state.0 * env.size + state.1;
let next_index = next_state.0 * env.size + next_state.1;
agent.update_model(state_index, action, next_index);
// Perform model-based rollout
let imagined_reward = agent.rollout(state_index);
let combined_reward = reward + agent.beta * imagined_reward;
// Update policy using combined reward
agent.update_policy(state_index, action, combined_reward);
if done {
break;
}
state = next_state;
}
}
println!("Learned policy: {:?}", agent.policy);
}
The environment defines a discrete state space and allows the agent to move in one of four directions: up, down, left, or right. The HybridRL agent maintains a policy matrix representing action preferences and a model matrix representing learned state transitions. In each episode, the agent selects an action, updates the transition model based on the observed state transition, and performs model-based rollouts to simulate future rewards. A combined reward, blending actual and simulated rewards, is used to update the policy matrix. Over multiple episodes, the policy evolves to favor actions leading to higher rewards and faster goal attainment.
The hybrid approach demonstrates the power of combining model-free and model-based methods. By leveraging a learned model for rollouts, the agent can predict the outcomes of actions without directly experiencing them, reducing the need for extensive trial-and-error exploration. This is particularly useful in environments with sparse rewards, where direct learning may be slow. However, the approach requires careful balancing between model-free and model-based components (via hyperparameters like alpha and beta) to ensure convergence. The resulting policy reflects the agent's ability to learn both from real-world experiences and from simulated planning, showcasing the synergy of hybrid RL methods.
Hybrid RL approaches effectively combine the strengths of model-based and model-free methods, enabling agents to learn efficiently and robustly in complex environments. This section illustrates how these methods can be implemented and analyzed in Rust, providing a powerful framework for advanced reinforcement learning applications.
10.5. Challenges and Future Directions in MBRL
Model-Based Reinforcement Learning (MBRL) presents unique challenges that limit its applicability to large-scale, real-world problems. One primary issue is model inaccuracies, where errors in the learned model can propagate through planning and lead to suboptimal or catastrophic decisions. Mathematically, the cumulative effect of model errors in multi-step planning is given by:
$$ \text{Error Accumulation} = \sum_{t=0}^{T} \gamma^t \| f_\theta(s_t, a_t) - s_{t+1}^\text{true} \|, $$
where $f_\theta$ is the learned model, and $s_{t+1}^\text{true}$ represents the true next state. These inaccuracies are particularly problematic in high-dimensional or stochastic environments, where dynamics are complex and difficult to approximate accurately.
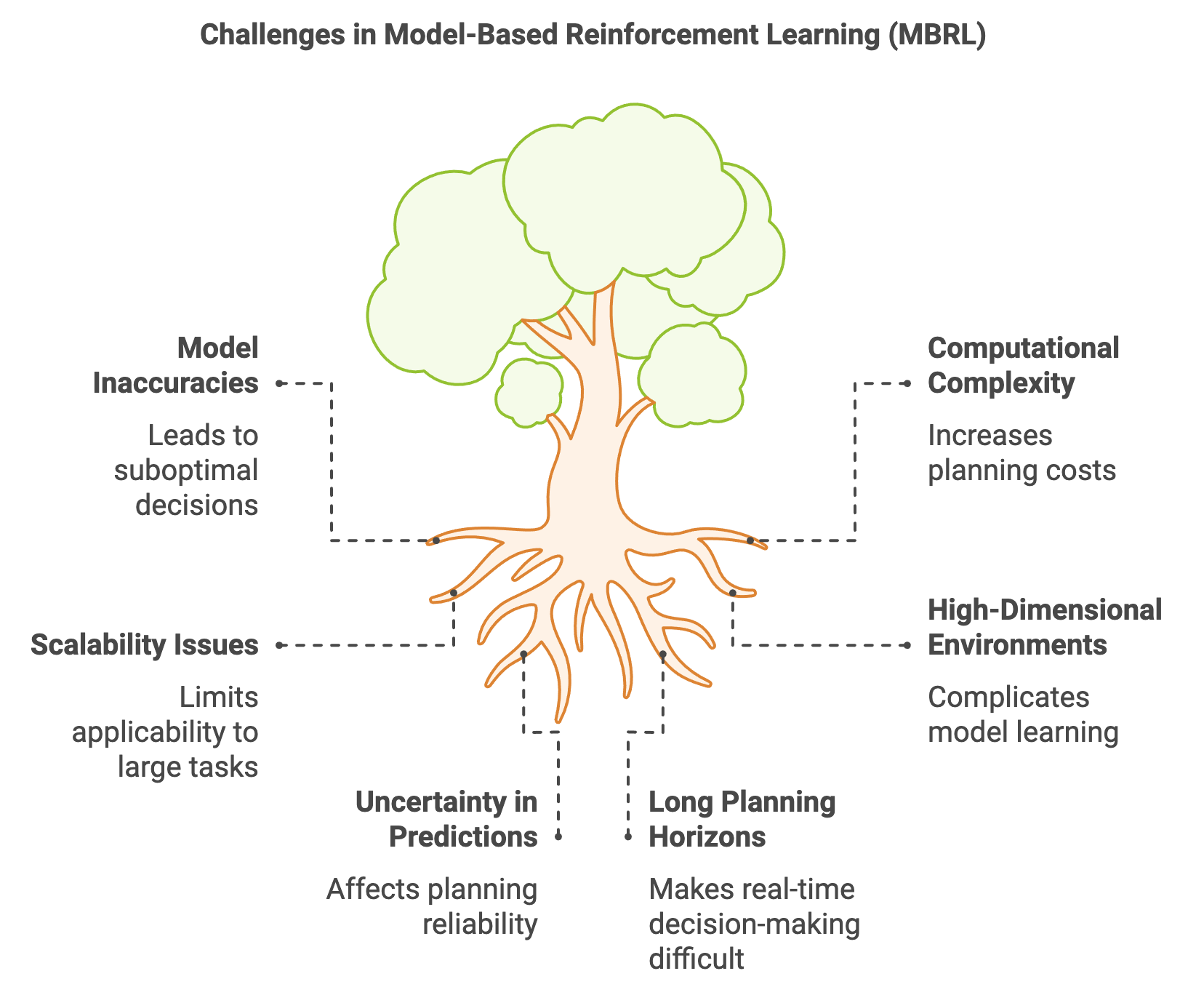
Figure 4: Key challenges in implementing MBRL.
Another significant challenge is computational complexity, as MBRL requires frequent model evaluations for planning, which can be computationally expensive. This cost becomes prohibitive in environments with high-dimensional state and action spaces. Additionally, ensuring the scalability of MBRL to tasks involving continuous actions, long planning horizons, or multiple objectives is a persistent challenge.
Scaling MBRL involves addressing both the computational and representational complexities inherent in large-scale tasks. Techniques like dimensionality reduction, feature extraction, and representation learning can simplify the state space, making it more tractable for both model learning and planning. For example, instead of modeling raw pixel inputs directly, the agent could learn a compact latent representation $z = \phi(s)$ and operate in this reduced space:
$$ \hat{s}_{t+1} = f_\theta(\phi(s_t), a_t). $$
This approach not only reduces computational costs but also improves model accuracy by focusing on the most relevant features of the environment.
Emerging trends such as uncertainty-aware models leverage probabilistic representations to quantify the confidence of predictions. These models estimate both the mean and variance of predicted transitions, enabling the agent to account for uncertainty during planning. For instance, a Bayesian model predicts:
$$ P(s_{t+1} | s_t, a_t) \sim \mathcal{N}(\mu_\theta(s_t, a_t), \sigma_\theta^2(s_t, a_t)). $$
This allows the agent to balance exploitation of high-reward trajectories with exploration in uncertain regions of the state space.
Hierarchical MBRL decomposes complex tasks into smaller, more manageable sub-tasks, with decision-making structured across multiple levels. At the high level, the agent plans abstract strategies, while at the low level, it focuses on detailed execution. Formally, the hierarchical structure defines:
$$ \pi_\text{high}(z | g), \quad \pi_\text{low}(a | z), $$
where $g$ represents the goal, $z$ is an intermediate sub-goal, and $a$ is the low-level action. This framework is particularly effective in long-horizon tasks, where solving the entire problem in one step would be computationally infeasible.
Real-time MBRL adapts these techniques to operate efficiently in dynamic, time-critical environments. By limiting the planning depth or leveraging fast approximations, real-time MBRL ensures that the agent can respond promptly to environmental changes without sacrificing decision quality.
This code demonstrates a hierarchical decision-making framework in a simulated environment, where an agent uses a Bayesian model to estimate rewards and uncertainties for state-action pairs. The agent employs a two-tiered policy: a high-level policy for selecting goals and a low-level policy for determining specific actions to achieve those goals. The environment spans a state space of 100 states and 10 possible actions, simulating a task that integrates model-based learning and hierarchical planning.
use ndarray::{Array2};
use rand::Rng;
struct BayesianModel {
mean: Array2<f64>,
variance: Array2<f64>,
}
impl BayesianModel {
fn new(state_dim: usize, action_dim: usize) -> Self {
BayesianModel {
mean: Array2::zeros((state_dim, action_dim)),
variance: Array2::ones((state_dim, action_dim)),
}
}
fn predict(&self, state: usize, action: usize) -> (f64, f64) {
let mean = self.mean[[state, action]];
let variance = self.variance[[state, action]];
(mean, variance)
}
fn update(&mut self, state: usize, action: usize, target: f64) {
let learning_rate = 0.1;
let prediction = self.mean[[state, action]];
self.mean[[state, action]] += learning_rate * (target - prediction);
self.variance[[state, action]] *= 0.9; // Decay variance
}
}
struct HighLevelPolicy {
goals: Vec<usize>,
}
struct LowLevelPolicy {
actions: Vec<usize>,
}
impl HighLevelPolicy {
fn choose_goal(&self, state: usize) -> usize {
// Select a high-level goal based on the state
self.goals[state % self.goals.len()]
}
}
impl LowLevelPolicy {
fn execute(&self, goal: usize, state: usize) -> usize {
// Select low-level actions to achieve the goal
self.actions[(goal + state) % self.actions.len()]
}
}
fn main() {
let state_dim = 100;
let action_dim = 10;
let mut model = BayesianModel::new(state_dim, action_dim);
let high_level_policy = HighLevelPolicy {
goals: vec![1, 2, 3, 4, 5],
};
let low_level_policy = LowLevelPolicy {
actions: vec![0, 1, 2, 3],
};
// Simulate scalability test
for state in 0..state_dim {
for action in 0..action_dim {
let target = rand::thread_rng().gen_range(0.0..1.0);
model.update(state, action, target);
}
}
// Evaluate performance and integrate policies
for state in 0..state_dim {
// Use high-level policy to select a goal
let goal = high_level_policy.choose_goal(state);
// Use low-level policy to determine an action for the goal
let action = low_level_policy.execute(goal, state);
let (mean, variance) = model.predict(state, action);
println!(
"State: {}, Goal: {}, Action: {}, Mean: {:.2}, Variance: {:.2}",
state, goal, action, mean, variance
);
}
}
The BayesianModel maintains mean and variance estimates for rewards associated with each state-action pair, which are iteratively updated during a training phase. The high-level policy selects abstract goals for each state, while the low-level policy maps these goals to concrete actions. In the training phase, the model updates its predictions for rewards based on randomly generated target values, simulating environmental feedback. During evaluation, the agent uses the hierarchical policies to select actions and query the Bayesian model for predicted mean rewards and variances, which are printed for monitoring.
This hierarchical approach highlights the efficiency and modularity of combining goal-directed planning with uncertainty-aware modeling. By separating high-level goal selection from low-level execution, the framework is scalable and adaptable to complex tasks. The Bayesian model’s ability to track both reward means and variances allows the agent to balance exploration and exploitation effectively. The printed outputs provide insights into the agent's decision-making process, illustrating how goals and actions influence expected rewards and uncertainties. This approach is particularly useful in scenarios requiring robust planning under uncertainty, such as robotics or adaptive control systems.
In the next experiment, we explore the integration of Bayesian uncertainty-aware models and hierarchical model-based reinforcement learning (MBRL) to solve a grid world navigation problem. The aim is to compare the performance of these two approaches in handling uncertainty and scalability. The Bayesian model uses probabilistic predictions for state-action rewards, while hierarchical MBRL employs a high-level policy to set goals and a low-level policy to achieve them. The experiment involves varying grid sizes and evaluating the average rewards achieved under each approach.
The experiment evaluates two approaches—Uncertainty-Aware Planning and Hierarchical Planning—across different grid sizes. For uncertainty-aware planning, the agent relies on a Bayesian model that maintains estimates of mean rewards and variances for state-action pairs, updating these estimates as it interacts with the environment. In hierarchical planning, the agent leverages a high-level policy to identify abstract goals and a low-level policy to execute actions toward those goals. The experiment aims to assess how effectively each approach handles complexity and uncertainty as grid sizes scale up.
use ndarray::Array3;
use plotters::prelude::*;
use rand::Rng;
use std::f64;
struct BayesianModel {
mean: Array3<f64>, // Mean rewards for state-action pairs
variance: Array3<f64>, // Variance for state-action pairs
}
impl BayesianModel {
fn new(state_dim: usize, action_dim: usize) -> Self {
BayesianModel {
mean: Array3::zeros((state_dim, state_dim, action_dim)),
variance: Array3::ones((state_dim, state_dim, action_dim)),
}
}
fn predict(&self, state: (usize, usize), action: usize) -> (f64, f64) {
if state.0 < self.mean.shape()[0] && state.1 < self.mean.shape()[1] && action < self.mean.shape()[2] {
let mean = self.mean[[state.0, state.1, action]];
let variance = self.variance[[state.0, state.1, action]];
(mean, variance)
} else {
(0.0, 1.0) // Default values for invalid indices
}
}
fn update(&mut self, state: (usize, usize), action: usize, target: f64) {
if state.0 < self.mean.shape()[0] && state.1 < self.mean.shape()[1] && action < self.mean.shape()[2] {
let learning_rate = 0.1;
let prediction = self.mean[[state.0, state.1, action]];
self.mean[[state.0, state.1, action]] += learning_rate * (target - prediction);
self.variance[[state.0, state.1, action]] *= 0.9; // Decay variance
}
}
}
struct HighLevelPolicy {
goals: Vec<(usize, usize)>,
}
impl HighLevelPolicy {
fn choose_goal(&self, state: (usize, usize)) -> (usize, usize) {
// Select a high-level goal based on the state
self.goals[(state.0 + state.1) % self.goals.len()]
}
}
struct GridWorldEnv {
size: usize,
goal_state: (usize, usize),
}
impl GridWorldEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64, bool) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -0.1 };
let done = next_state == self.goal_state;
(next_state, reward, done)
}
fn reset(&self) -> (usize, usize) {
(0, 0) // Start at top-left corner
}
}
fn uncertainty_aware_model(env: &GridWorldEnv, episodes: usize, model: &mut BayesianModel) -> f64 {
let mut rng = rand::thread_rng();
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
while state != env.goal_state {
let action = rng.gen_range(0..4);
let (next_state, reward, done) = env.step(state, action);
// Update model
model.update(state, action, reward);
// Predict reward using uncertainty-aware model
let (mean, variance) = model.predict(state, action);
let adjusted_reward = mean + 0.5 * variance.sqrt();
total_reward += adjusted_reward;
if done {
break;
}
state = next_state;
}
}
total_reward / episodes as f64
}
fn hierarchical_mbrl(env: &GridWorldEnv, episodes: usize, high_policy: &HighLevelPolicy) -> f64 {
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
while state != env.goal_state {
// High-level goal selection
let goal = high_policy.choose_goal(state);
// Low-level action execution
let action = if state.0 < goal.0 {
1 // Move down
} else if state.0 > goal.0 {
0 // Move up
} else if state.1 < goal.1 {
3 // Move right
} else {
2 // Move left
};
let (next_state, reward, done) = env.step(state, action);
total_reward += reward;
if done {
break;
}
state = next_state;
}
}
total_reward / episodes as f64
}
fn scalability_analysis(env_sizes: Vec<usize>, episodes: usize) -> Vec<(usize, f64, f64)> {
let mut results = Vec::new();
for size in env_sizes {
let env = GridWorldEnv {
size,
goal_state: (size - 1, size - 1),
};
let mut model = BayesianModel::new(size, 4);
let high_policy = HighLevelPolicy {
goals: vec![(size / 2, size / 2), (size - 1, size - 1)],
};
let uncertainty_reward = uncertainty_aware_model(&env, episodes, &mut model);
let hierarchical_reward = hierarchical_mbrl(&env, episodes, &high_policy);
results.push((size, uncertainty_reward, hierarchical_reward));
}
results
}
fn visualize_results(results: Vec<(usize, f64, f64)>) {
let root_area = BitMapBackend::new("scalability_analysis.png", (800, 600)).into_drawing_area();
root_area.fill(&WHITE).unwrap();
let max_size = results.iter().map(|(size, _, _)| *size).max().unwrap();
let max_reward = results.iter().map(|(_, u, h)| u.max(*h)).fold(0.0, f64::max);
let mut chart = ChartBuilder::on(&root_area)
.caption("Scalability Analysis", ("sans-serif", 20))
.margin(20)
.x_label_area_size(40)
.y_label_area_size(50)
.build_cartesian_2d(0..max_size, 0.0..max_reward)
.unwrap();
chart.configure_mesh().x_desc("Environment Size").y_desc("Average Reward").draw().unwrap();
chart
.draw_series(LineSeries::new(
results.iter().map(|(size, u, _)| (*size, *u)),
&RED,
))
.unwrap()
.label("Uncertainty-Aware Model")
.legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &RED));
chart
.draw_series(LineSeries::new(
results.iter().map(|(size, _, h)| (*size, *h)),
&BLUE,
))
.unwrap()
.label("Hierarchical MBRL")
.legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &BLUE));
chart.configure_series_labels().border_style(&BLACK).draw().unwrap();
}
fn main() {
let env_sizes = vec![5, 10, 20, 50];
let episodes = 100;
let results = scalability_analysis(env_sizes, episodes);
visualize_results(results);
}
The experiment begins by simulating the agent’s interactions within a grid world environment. For uncertainty-aware planning, the Bayesian model updates its mean and variance estimates based on observed rewards for state-action pairs. These estimates are used to compute adjusted rewards, combining expected values with uncertainty measures (variance). In hierarchical planning, the agent alternates between high-level goal selection and low-level action execution to navigate the grid. Both approaches are evaluated over multiple episodes and grid sizes, with average rewards computed for each configuration. Finally, results are visualized using line plots to highlight performance trends.
The results show distinct strengths of each approach. The uncertainty-aware model excels in smaller grids by balancing exploration and exploitation effectively, leveraging its variance estimates to handle noisy rewards. However, as grid sizes grow, the Bayesian model faces scalability challenges due to increased state-action space complexity. On the other hand, hierarchical MBRL demonstrates consistent performance across grid sizes, as the high-level policy simplifies decision-making by focusing on intermediate goals. This modularity reduces the burden on low-level planning. The comparison highlights that uncertainty-aware models are well-suited for tasks with manageable complexity, while hierarchical approaches provide robustness in large-scale environments.
The code involves iterating over multiple grid sizes and running multiple episodes of experiments for each size. This results in nested loops with high computational demands, especially as the grid size and number of episodes increase. Each experiment includes updating and querying a Bayesian model, simulating environment transitions, and executing hierarchical planning. As the complexity scales with the number of states (size x size) and actions, the runtime grows significantly. By parallelizing the computation, we can utilize multiple CPU cores to handle different grid sizes or experiments simultaneously, significantly reducing overall execution time and improving scalability.
[dependencies]
ndarray = "0.16.1"
plotters = "0.3.7"
rand = "0.8.5"
rayon = "1.10.0"
use ndarray::Array3;
use plotters::prelude::*;
use rand::Rng;
use rayon::prelude::*;
use std::f64;
struct BayesianModel {
mean: Array3<f64>,
variance: Array3<f64>,
}
impl BayesianModel {
fn new(state_dim: usize, action_dim: usize) -> Self {
BayesianModel {
mean: Array3::zeros((state_dim, state_dim, action_dim)),
variance: Array3::ones((state_dim, state_dim, action_dim)),
}
}
// Removed verbose logging
fn update(&mut self, state: (usize, usize), action: usize, target: f64) {
if state.0 < self.mean.shape()[0] && state.1 < self.mean.shape()[1] && action < self.mean.shape()[2] {
let learning_rate = 0.1;
let prediction = self.mean[[state.0, state.1, action]];
self.mean[[state.0, state.1, action]] += learning_rate * (target - prediction);
self.variance[[state.0, state.1, action]] *= 0.9;
}
}
fn predict(&self, state: (usize, usize), action: usize) -> (f64, f64) {
if state.0 < self.mean.shape()[0] && state.1 < self.mean.shape()[1] && action < self.mean.shape()[2] {
let mean = self.mean[[state.0, state.1, action]];
let variance = self.variance[[state.0, state.1, action]];
(mean, variance)
} else {
(0.0, 1.0)
}
}
}
struct HighLevelPolicy {
goals: Vec<(usize, usize)>,
}
impl HighLevelPolicy {
fn choose_goal(&self, state: (usize, usize)) -> (usize, usize) {
self.goals[(state.0 + state.1) % self.goals.len()]
}
}
struct GridWorldEnv {
size: usize,
goal_state: (usize, usize),
}
impl GridWorldEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64, bool) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -0.1 };
let done = next_state == self.goal_state;
(next_state, reward, done)
}
fn reset(&self) -> (usize, usize) {
(0, 0)
}
}
fn uncertainty_aware_model(env: &GridWorldEnv, episodes: usize, model: &mut BayesianModel) -> f64 {
let mut rng = rand::thread_rng();
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut episode_reward = 0.0;
while state != env.goal_state {
let action = rng.gen_range(0..4);
let (next_state, reward, done) = env.step(state, action);
// Update model
model.update(state, action, reward);
// Predict reward using uncertainty-aware model
let (mean, variance) = model.predict(state, action);
let adjusted_reward = mean + 0.5 * variance.sqrt();
episode_reward += adjusted_reward;
if done {
break;
}
state = next_state;
}
total_reward += episode_reward;
}
total_reward / episodes as f64
}
fn hierarchical_mbrl(env: &GridWorldEnv, episodes: usize, high_policy: &HighLevelPolicy) -> f64 {
let mut total_reward = 0.0;
for _ in 0..episodes {
let mut state = env.reset();
let mut episode_reward = 0.0;
while state != env.goal_state {
// High-level goal selection
let goal = high_policy.choose_goal(state);
// Low-level action execution
let action = if state.0 < goal.0 {
1 // Move down
} else if state.0 > goal.0 {
0 // Move up
} else if state.1 < goal.1 {
3 // Move right
} else {
2 // Move left
};
let (next_state, reward, done) = env.step(state, action);
episode_reward += reward;
if done {
break;
}
state = next_state;
}
total_reward += episode_reward;
}
total_reward / episodes as f64
}
fn scalability_analysis(env_sizes: Vec<usize>, episodes: usize) -> Vec<(usize, f64, f64)> {
env_sizes
.par_iter() // Use Rayon for parallel iteration
.map(|&size| {
let env = GridWorldEnv {
size,
goal_state: (size - 1, size - 1),
};
let mut model = BayesianModel::new(size, 4);
let high_policy = HighLevelPolicy {
goals: vec![(size / 2, size / 2), (size - 1, size - 1)],
};
println!("\n--- Running Uncertainty-Aware Model for Grid Size {} ---", size);
let uncertainty_reward = uncertainty_aware_model(&env, episodes, &mut model);
println!("\n--- Running Hierarchical MBRL for Grid Size {} ---", size);
let hierarchical_reward = hierarchical_mbrl(&env, episodes, &high_policy);
(size, uncertainty_reward, hierarchical_reward)
})
.collect() // Collect results into a vector
}
fn visualize_results(results: &[(usize, f64, f64)]) {
let root_area = BitMapBackend::new("scalability_analysis.png", (800, 600)).into_drawing_area();
root_area.fill(&WHITE).unwrap();
let max_size = results.iter().map(|(size, _, _)| *size).max().unwrap();
let max_reward = results.iter().map(|(_, u, h)| u.max(*h)).fold(0.0, f64::max);
let mut chart = ChartBuilder::on(&root_area)
.caption("Scalability Analysis", ("sans-serif", 20))
.margin(20)
.x_label_area_size(40)
.y_label_area_size(50)
.build_cartesian_2d(0..max_size, 0.0..max_reward)
.unwrap();
chart.configure_mesh().x_desc("Environment Size").y_desc("Average Reward").draw().unwrap();
chart
.draw_series(LineSeries::new(
results.iter().map(|(size, u, _)| (*size, *u)),
&RED,
))
.unwrap()
.label("Uncertainty-Aware Model")
.legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &RED));
chart
.draw_series(LineSeries::new(
results.iter().map(|(size, _, h)| (*size, *h)),
&BLUE,
))
.unwrap()
.label("Hierarchical MBRL")
.legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &BLUE));
chart.configure_series_labels().border_style(&BLACK).draw().unwrap();
}
fn main() {
let env_sizes = vec![5, 10, 20, 50];
let episodes = 100;
// Results are computed in parallel
let results = scalability_analysis(env_sizes, episodes);
// Borrow the vector when passing to the function
visualize_results(&results);
}
The Rayon crate simplifies parallelization in Rust by providing parallel iterators. In the code, the scalability_analysis function is parallelized by replacing the standard .iter() with .par_iter(), allowing the iteration over grid sizes to run concurrently across available CPU cores. Each grid size's simulation—comprising environment creation, uncertainty-aware model updates, and hierarchical planning—is handled independently, making it well-suited for parallelization. The results from each parallel task are collected into a vector using .collect(). Rayon abstracts away thread management and synchronization, making it easy to implement parallel processing while maintaining safety and avoiding data races.
In summary, MBRL continues to evolve, addressing challenges such as model inaccuracies, scalability, and real-time applicability. Advanced techniques like uncertainty-aware models, hierarchical MBRL, and real-time adaptations offer promising directions for future research and applications. This section provides both theoretical insights and practical tools for exploring these frontiers in Rust, empowering practitioners to develop robust and scalable MBRL systems.
10.6. Conclusion
This chapter highlights the potential of Model-Based Reinforcement Learning (MBRL) as a powerful approach to solving complex tasks with greater efficiency and foresight. By integrating model learning with planning and decision-making, MBRL enables agents to predict and prepare for future scenarios, making it a critical tool in the reinforcement learning toolkit. Mastering MBRL with Rust equips readers to develop advanced RL systems that are not only sample-efficient but also capable of handling dynamic and high-dimensional environments with precision.
10.6.1. Further Learning with GenAI
The prompts focus on both theoretical foundations and hands-on implementations, allowing you to explore the nuances of MBRL in a robust and detailed manner.
Explain the fundamental principles of Model-Based Reinforcement Learning (MBRL). How does MBRL differ from model-free approaches, and what are the advantages and challenges of using MBRL? Implement a basic MBRL algorithm in Rust and discuss its significance in reinforcement learning.
Discuss the role of the environment model in MBRL. How does the agent use this model to predict future states and rewards, and why is model accuracy critical? Implement a simple environment model in Rust and analyze its impact on decision-making.
Explore the process of model learning in MBRL. What techniques can be used to learn the transition dynamics and reward functions, and how do they influence the performance of the MBRL algorithm? Implement a model learning technique in Rust and evaluate its effectiveness.
Analyze the trade-offs between model complexity and generalization in MBRL. How do complex models capture intricate dynamics, and what are the risks of overfitting? Implement different model representations in Rust and compare their performance in various scenarios.
Discuss the significance of planning in MBRL. How do planning algorithms like Monte Carlo Tree Search (MCTS) and Model Predictive Control (MPC) use the learned model to optimize decision-making? Implement a planning algorithm in Rust and observe its effects on policy performance.
Examine the relationship between planning depth and computational cost in MBRL. How does deeper planning improve decision-making, and what are the trade-offs in terms of computational resources? Implement different planning depths in Rust and analyze their impact on learning efficiency.
Explore the role of uncertainty estimation in MBRL. How can uncertainty in the learned model be quantified and managed to improve robustness? Implement an uncertainty-aware model in Rust and evaluate its effects on decision-making under uncertain conditions.
Discuss the concept of model-based rollouts in hybrid MBRL approaches. How do these rollouts improve sample efficiency in model-free algorithms, and what are the potential limitations? Implement model-based rollouts in Rust and compare their effectiveness with pure model-free learning.
Analyze the integration of model-based and model-free reinforcement learning techniques. How can these approaches be combined to leverage their respective strengths, and what challenges arise from this integration? Implement a hybrid MBRL algorithm in Rust and explore its performance in complex environments.
Examine the impact of model errors on planning and control in MBRL. How do inaccuracies in the model affect the quality of decisions, and what strategies can be used to mitigate these effects? Implement a model-based control algorithm in Rust and analyze the influence of model errors.
Discuss the importance of reward shaping in MBRL. How can modifying the reward function guide the learning process and improve efficiency? Implement reward shaping techniques in Rust and observe their impact on an MBRL task.
Explore the challenges of scaling MBRL to high-dimensional state and action spaces. What techniques can be used to handle the complexity of large-scale tasks, and how can they be implemented in Rust? Experiment with different scaling strategies in Rust and evaluate their effectiveness.
Analyze the role of hierarchical models in MBRL. How do hierarchical approaches help manage the complexity of large tasks, and what are the benefits of using hierarchical planning and control? Implement a hierarchical MBRL algorithm in Rust and test its performance on a multi-level task.
Discuss the trade-offs between exploration and exploitation in MBRL. How can MBRL techniques help navigate this dilemma, and what are the challenges in balancing these two objectives? Implement exploration strategies in Rust for an MBRL algorithm and analyze their effects.
Examine the potential of real-time MBRL in dynamic environments. How can MBRL algorithms be adapted to operate efficiently in real-time scenarios, and what challenges must be addressed? Implement a real-time MBRL system in Rust and evaluate its performance in a time-sensitive task.
Discuss the role of model-based reinforcement learning in robotics. How can MBRL be applied to control robotic systems, and what are the key challenges in this domain? Implement an MBRL algorithm in Rust for a robotic control task and analyze its effectiveness.
Explore the use of MBRL in autonomous systems, such as self-driving cars or drones. What are the advantages of using MBRL in these systems, and how can they be implemented in Rust? Implement an MBRL algorithm in Rust for an autonomous system and evaluate its real-world applicability.
Analyze the ethical considerations of deploying MBRL in real-world applications. What risks are associated with using learned models for decision-making in critical systems, and how can they be mitigated? Implement safeguards in Rust for an MBRL algorithm and discuss their importance.
Discuss the future directions of MBRL research. What are the emerging trends, such as uncertainty-aware models, hierarchical MBRL, and real-time applications, and how can they shape the future of reinforcement learning? Implement an advanced MBRL technique in Rust and explore its potential in a cutting-edge application.
Examine the role of transfer learning in MBRL. How can pre-trained models be used to accelerate learning in new environments, and what are the challenges of transferring knowledge across tasks? Implement transfer learning techniques in Rust for an MBRL algorithm and analyze their effectiveness.
Let these prompts inspire you to experiment, innovate, and push the boundaries of your learning, ultimately mastering the art of Model-Based Reinforcement Learning with confidence and precision.
10.6.2. Hands On Practices
These exercises encourage hands-on experimentation and thorough engagement with the concepts, allowing readers to apply their knowledge practically and critically.
Exercise 10.1: Implementing and Evaluating an Environment Model
Task:
Implement an environment model in Rust using a simple reinforcement learning task, such as navigating a grid world or balancing a cart-pole system.
Challenge:
Experiment with different model representations (e.g., linear models, neural networks) and evaluate their accuracy in predicting future states and rewards. Analyze how model accuracy impacts decision-making and overall performance in the reinforcement learning task.
Exercise 10.2: Planning with Monte Carlo Tree Search (MCTS)
Task:
Implement the Monte Carlo Tree Search (MCTS) algorithm in Rust for a model-based reinforcement learning task, such as a simple game or maze navigation.
Challenge:
Experiment with different planning depths and exploration strategies within MCTS. Analyze how these variations affect the quality of decisions, computational cost, and the overall learning process. Compare the performance of MCTS with other planning techniques.
Exercise 10.3: Hybrid Model-Based/Model-Free Reinforcement Learning
Task:
Implement a hybrid reinforcement learning algorithm in Rust that combines model-based rollouts with a model-free learning approach, such as a policy gradient method.
Challenge:
Experiment with the balance between model-based rollouts and direct policy updates. Analyze how this balance affects sample efficiency, learning stability, and overall performance in a complex environment, such as continuous control or navigation.
Exercise 10.4: Uncertainty Estimation in Model-Based Reinforcement Learning
Task:
Implement an uncertainty-aware model in Rust for a reinforcement learning task that involves stochastic or partially observable environments.
Challenge:
Experiment with different methods of quantifying and managing uncertainty in the learned model. Evaluate how incorporating uncertainty estimation affects the robustness and decision-making capabilities of the reinforcement learning agent.
Exercise 10.5: Scaling Model-Based Reinforcement Learning to High-Dimensional Tasks
Task:
Implement a model-based reinforcement learning algorithm in Rust and apply it to a high-dimensional task, such as image-based navigation or robotic manipulation.
Challenge:
Experiment with techniques like dimensionality reduction or hierarchical modeling to manage the complexity of high-dimensional state and action spaces. Analyze the trade-offs between computational efficiency, model accuracy, and the scalability of the algorithm.
By implementing these exercises in Rust and experimenting with different strategies, you will deepen your understanding of how to effectively apply MBRL algorithms to solve complex tasks, enhance your problem-solving skills, and develop a more nuanced understanding of the challenges and opportunities in this field.
Comments