Chapter 6
Temporal-Difference Learning
"Temporal-Difference learning stands at the heart of reinforcement learning, blending the elegance of theory with the power of practical implementation." — Richard Sutton
Chapter 6 of RLVR provides an in-depth exploration of Temporal-Difference (TD) learning, a crucial methodology in reinforcement learning that combines the strengths of both Monte Carlo methods and dynamic programming. This chapter begins with an introduction to the fundamentals of TD learning, explaining how it enables value updates after each step of an episode, rather than waiting for its conclusion. Readers will gain a solid understanding of key concepts such as bootstrapping, TD error, and the significance of real-time updates in achieving computational efficiency. The chapter then delves into SARSA, an on-policy TD control method, illustrating how it updates the policy based on actual actions taken and explores the balance between exploration and exploitation. Practical Rust implementations help solidify understanding by guiding readers through building SARSA for various tasks. The chapter also covers Q-Learning, a powerful off-policy TD method that updates the value function based on the optimal action, offering flexibility in learning the optimal policy while following a different behavior policy. This section provides hands-on exercises in Rust, emphasizing the differences between on-policy and off-policy learning. Next, the chapter introduces n-Step TD methods, which extend TD(0) by considering multiple steps before making an update, offering a spectrum of algorithms that bridge the gap between TD and Monte Carlo methods. The final section discusses eligibility traces and TD(λ), a generalization of TD methods that uses eligibility traces to combine short-term and long-term returns, offering a flexible approach to credit assignment in RL. Through this comprehensive chapter, readers will gain both theoretical insights and practical experience in implementing, experimenting with, and optimizing TD learning algorithms using Rust.
6.1. Introduction to Temporal-Difference (TD) Learning
Temporal-Difference (TD) learning methods are a cornerstone of modern reinforcement learning, tracing their origins to the foundational principles of dynamic programming and Monte Carlo methods. These two paradigms shaped early approaches to sequential decision-making, but their limitations spurred the development of more flexible and efficient learning algorithms.
Dynamic programming, pioneered by Richard Bellman in the 1950s, introduced the Bellman equation as a framework for solving sequential decision problems. The Bellman equation provided a way to decompose complex problems into smaller, manageable subproblems, laying the groundwork for algorithms such as policy iteration and value iteration. These methods relied on the principle of bootstrapping—updating value estimates based on the values of successor states. However, dynamic programming techniques required a complete model of the environment’s dynamics, including transition probabilities and rewards. Additionally, their computational cost made them impractical for large or high-dimensional state spaces.
Monte Carlo methods emerged as an alternative in the 1970s, offering a model-free approach to learning value functions by sampling returns from complete episodes. Unlike dynamic programming, Monte Carlo methods did not require explicit knowledge of the environment, making them more versatile. However, their reliance on full episodes for updates introduced delays and inefficiencies, particularly in environments with long episodes or continuous tasks.
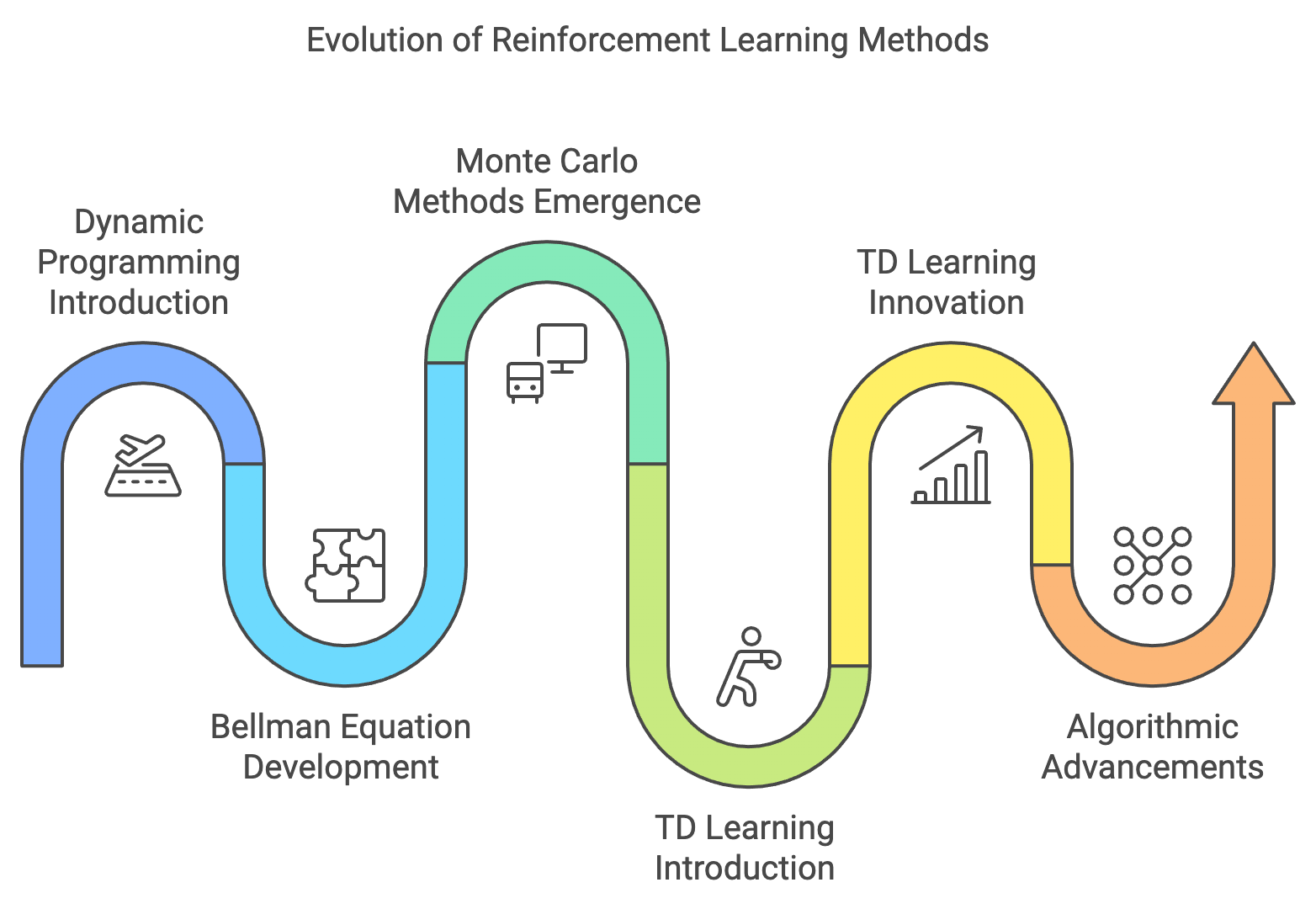
Figure 1: Key milestone and evolution of RL methods.
In the late 20th century, researchers sought to combine the strengths of dynamic programming’s bootstrapping and Monte Carlo’s model-free learning. This effort culminated in Richard Sutton’s seminal work in 1988, where he introduced the concept of Temporal-Difference (TD) learning in his paper Learning to Predict by the Methods of Temporal Differences. TD learning proposed a novel framework that leveraged bootstrapping to update value estimates incrementally after each step, rather than waiting for the end of an episode.
The key innovation of TD learning was its ability to update value functions using temporal differences—the discrepancy between successive value estimates. This incremental approach allowed TD methods to operate in real-time, adapting quickly to changing environments and enabling learning in continuous or ongoing tasks. By combining the advantages of Monte Carlo’s sample-based learning and dynamic programming’s bootstrapping, TD learning provided a versatile and efficient method for reinforcement learning.
The introduction of TD learning revolutionized reinforcement learning and paved the way for subsequent algorithmic advancements. Key developments include:
TD(λ): Extending TD learning with eligibility traces, TD(λ) generalized the algorithm to incorporate returns over multiple steps, creating a continuum between TD(0) (single-step updates) and Monte Carlo methods (full-episode updates).
Q-Learning: An off-policy TD control algorithm introduced by Chris Watkins in 1989, Q-Learning built on TD principles to learn optimal policies while allowing exploratory behavior.
Actor-Critic Methods: Combining TD learning with policy-based approaches, Actor-Critic methods leveraged TD updates to guide policy improvements, enabling efficient learning in complex environments.
TD methods became the foundation for deep reinforcement learning advancements in the 2010s, where they were integrated with neural networks to tackle high-dimensional and complex tasks. For example, Deep Q-Networks (DQNs) use TD principles to update action-value functions while leveraging deep learning for function approximation.
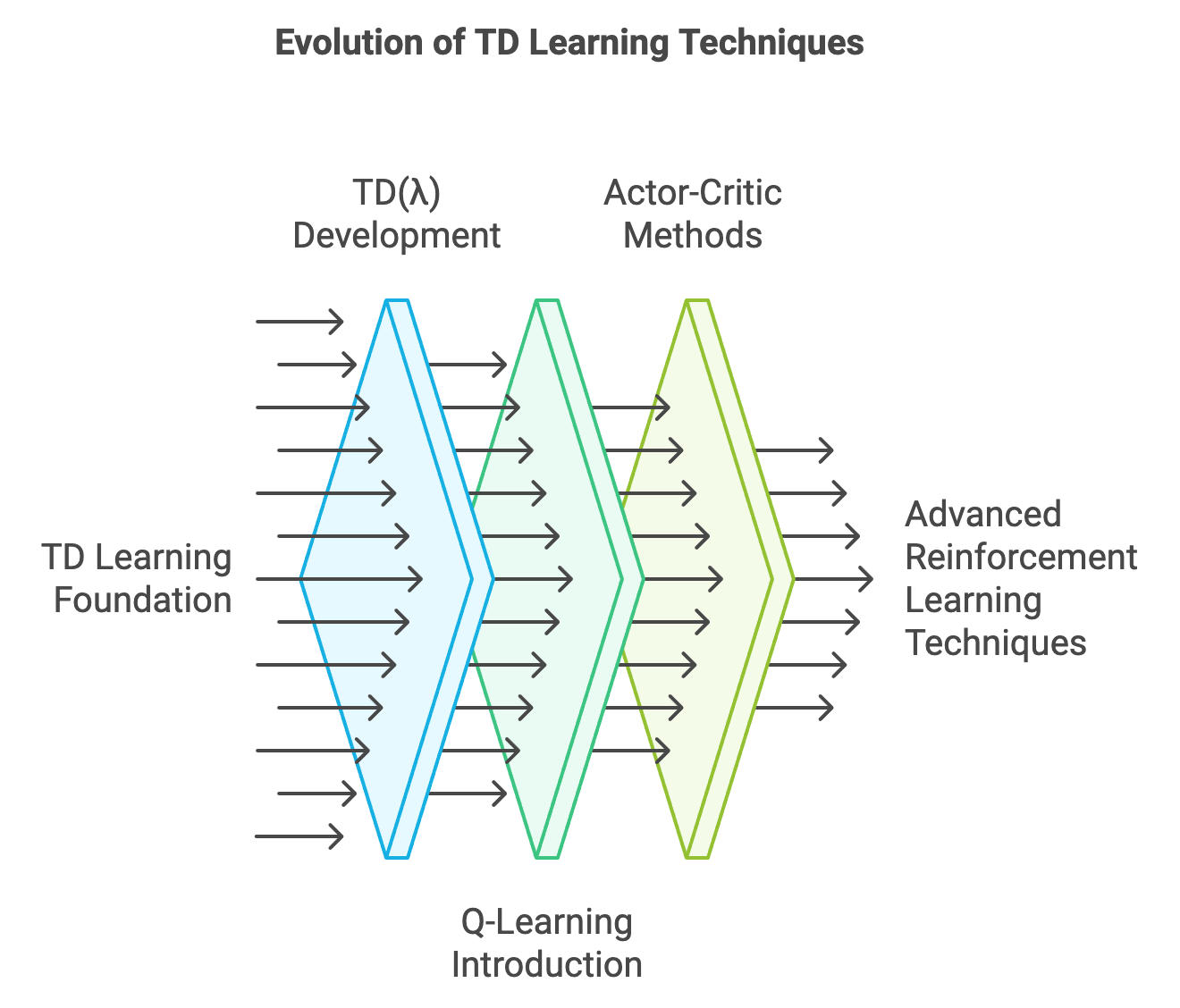
Figure 2: The evolution of TD learning with three major milestones.
At its core, Temporal-Difference learning is characterized by its incremental updates and reliance on bootstrapping. Unlike Monte Carlo methods, which estimate returns based on complete episodes, TD learning updates value functions using:
$$ V(s) \leftarrow V(s) + \alpha [r + \gamma V(s') - V(s)], \text{or} $$
$$V(s) \leftarrow V(s) + \alpha \delta.$$
where $V(s)$ is the value of the current state, $r$ is the immediate reward, $\gamma$ is the discount factor, and $V(s')$ is the value of the next state, $\alpha$ is the learning rate, and $\delta=r + \gamma V(s') - V(s)$ is TD error. This formulation enables agents to update their estimates after each transition, adapting to new information in real-time.
The flexibility and efficiency of TD learning have made it an enduring and fundamental method in reinforcement learning. Its adaptability to dynamic and stochastic environments, combined with its compatibility with both tabular and function approximation methods, ensures its continued relevance in advancing the field.
The core idea behind TD learning is the TD error, which represents the difference between the expected value of a state and the observed reward-plus-discounted-value of the next state. The TD error serves as the driving force for learning, guiding updates to the value function. Mathematically, the TD error is expressed as:
$$\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t),$$
where:
$\delta_t$ is the TD error at time $t$,
$R_{t+1}$ is the reward observed after transitioning to the next state $S_{t+1}$,
$V(S_t)$ and $V(S_{t+1})$ are the value estimates of the current and next states,
$\gamma$ is the discount factor, determining the importance of future rewards.
By incrementally updating the value function $V(S_t)$ using the TD error, TD learning achieves faster convergence compared to Monte Carlo methods while maintaining the flexibility of a model-free approach.
Temporal-Difference (TD) learning can be likened to how an investor updates their understanding of a stock’s value throughout the day. Instead of waiting for the end-of-day report to make adjustments, the investor reacts to real-time price fluctuations, incorporating new information step by step. This dynamic approach allows for quicker adaptation to market changes, mirroring how TD learning updates value estimates incrementally during an episode rather than waiting for its conclusion.
The defining feature of Temporal-Difference (TD) learning is bootstrapping, a process where value updates rely on current estimates of future values rather than waiting for full returns. This mechanism allows TD learning to balance computational efficiency with real-time adaptability. Bootstrapping distinguishes TD learning from two other foundational paradigms: Monte Carlo methods and dynamic programming.
Monte Carlo methods compute the value of a state or action based on the average returns observed over entire episodes. While this approach provides unbiased estimates, it requires waiting until the episode concludes before making updates. This delay makes Monte Carlo methods less efficient in environments with long or continuous episodes, where immediate updates are desirable. Dynamic programming, on the other hand, relies on a complete model of the environment's dynamics, including transition probabilities and reward functions. By systematically solving the Bellman equation, dynamic programming provides optimal solutions but requires full knowledge of the environment, limiting its applicability in scenarios where the model is unknown or too complex to compute.
TD learning bridges these two approaches by enabling incremental updates based solely on observed transitions and the agent’s current estimates. It is model-free, requiring no prior knowledge of the environment, and supports real-time learning, making it a versatile and practical method for reinforcement learning.
One of the primary advantages of TD learning is its ability to perform real-time updates, which enables agents to adapt during ongoing interactions with the environment. This characteristic is particularly valuable in several scenarios. First, for tasks with long or continuous episodes, waiting until the end of the episode to update values, as in Monte Carlo methods, would significantly delay learning. Second, in dynamic environments where conditions can change rapidly, real-time updates allow the agent to respond immediately, ensuring its value estimates remain relevant. Lastly, when data is sparse or costly to obtain, TD learning’s incremental updates make the most of every observed transition, maximizing learning efficiency.
Consider, for example, a robotic navigation task. TD learning enables the robot to adjust its path based on immediate feedback, such as avoiding obstacles or finding a shortcut, without needing to complete its journey before learning. This incremental approach not only improves efficiency but also ensures adaptability in real-world environments that are often unpredictable and dynamic.
The principles of TD learning have broad implications for reinforcement learning. By updating values step-by-step, TD learning minimizes delays and reduces computational overhead, making it highly efficient. Additionally, it scales well to large or infinite state spaces when combined with function approximation techniques, enabling its application to complex problems. Furthermore, TD methods are highly versatile, suitable for both episodic tasks with clear endpoints and continuous tasks that require ongoing adaptation. These characteristics make TD learning indispensable for a wide range of applications, including games, robotics, finance, and healthcare.
By combining the strengths of Monte Carlo methods and dynamic programming while overcoming their limitations, TD learning has become a cornerstone of reinforcement learning. Its ability to update estimates in real time using bootstrapping and TD errors allows agents to learn efficiently and effectively, even in complex and dynamic environments.
TD(0) is the simplest form of TD learning, where updates to the value function are based solely on the immediate transition between states. The update rule for TD(0) is:
$$ V(S_t) \leftarrow V(S_t) + \alpha \delta_t, $$
where:
$\alpha$ is the learning rate, controlling the magnitude of updates,
$\delta_t$ is the TD error, as defined earlier.
The learning rate $\alpha$ determines how quickly the agent adapts to new information, while the discount factor $\gamma$ balances the emphasis between immediate and future rewards. A higher $\gamma$ places more weight on future rewards, while a lower $\gamma$ prioritizes immediate outcomes.
Temporal Difference (TD) learning is a foundational reinforcement learning (RL) approach that combines the strengths of Monte Carlo (MC) methods and Dynamic Programming (DP). Unlike MC, which relies on complete episodes to update value functions, TD updates estimates incrementally after each step, allowing it to learn directly from incomplete episodes. The provided code implements TD(0), the simplest form of TD learning, to estimate the value function for a grid-world environment. TD(0) uses bootstrapping, where updates are based on the current reward and the value of the next state, enabling faster and more efficient learning in environments with stochastic or dynamic transitions.
use std::collections::HashMap;
use rand::Rng;
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 }; // Goal state has no penalty
(next_state, reward)
}
}
// Apply TD(0) to estimate the value function
fn td_zero(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
while state != grid_world.goal_state {
let action = rng.gen_range(0..4); // Random action selection
let (next_state, reward) = grid_world.step(state, action);
let current_value = *value_function.get(&state).unwrap_or(&0.0);
let next_value = *value_function.get(&next_state).unwrap_or(&0.0);
// Compute TD error and update value function
let td_error = reward + gamma * next_value - current_value;
value_function
.entry(state)
.and_modify(|v| *v += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
}
}
value_function
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
let value_function = td_zero(&grid_world, episodes, alpha, gamma);
println!("Estimated Value Function: {:?}", value_function);
}
The td_zero function iteratively updates the value function for each state in the grid-world environment. For a fixed number of episodes, the agent starts at the initial state and takes random actions to explore the environment. Each action results in a transition to a new state, with a reward of $-1$ for non-goal states and $0$ for the goal state. The value function for the current state is updated based on the TD error, which is the difference between the observed reward plus the discounted value of the next state and the current estimate. This error is scaled by the learning rate ($\alpha$) to adjust the value incrementally. By iteratively applying this process, the value function converges to an estimate that reflects the expected cumulative reward for each state, enabling the agent to evaluate states effectively without requiring complete episodes.
The revised Rust code below builds upon the initial version by incorporating dynamic visualizations of how varying learning rates ($\alpha$) and discount factors ($\gamma$) influence the temporal difference (TD(0)) learning process. Unlike the initial version, which merely printed the resulting value function for different parameters, this version utilizes the plotters crate to generate a consolidated visualization. These visualizations provide an intuitive representation of the value function's convergence across different parameter settings, making it easier to analyze the effects of $\alpha$ and $\gamma$ on learning.
use std::collections::HashMap;
use plotters::prelude::*;
use rand::Rng;
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 };
(next_state, reward)
}
}
fn td_zero(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0);
while state != grid_world.goal_state {
let action = rng.gen_range(0..4);
let (next_state, reward) = grid_world.step(state, action);
let current_value = *value_function.get(&state).unwrap_or(&0.0);
let next_value = *value_function.get(&next_state).unwrap_or(&0.0);
let td_error = reward + gamma * next_value - current_value;
value_function
.entry(state)
.and_modify(|v| *v += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
}
}
value_function
}
fn visualize_results(
results: &Vec<(f64, f64, HashMap<(usize, usize), f64>)>,
grid_size: usize,
output_path: &str,
) {
let root = BitMapBackend::new(output_path, (1024, 1024)).into_drawing_area();
root.fill(&WHITE).unwrap();
let areas = root.split_evenly((3, 3)); // Assuming 3x3 grid for alpha and gamma combinations
for (idx, ((alpha, gamma, value_function), area)) in results.iter().zip(areas.iter()).enumerate()
{
let mut chart = ChartBuilder::on(area)
.caption(format!("Alpha: {}, Gamma: {}", alpha, gamma), ("sans-serif", 15))
.margin(10)
.x_label_area_size(20)
.y_label_area_size(20)
.build_cartesian_2d(0..grid_size as i32, 0..grid_size as i32)
.unwrap();
chart.configure_mesh().draw().unwrap();
for ((x, y), value) in value_function {
let intensity = (*value).max(-10.0).min(0.0) / -10.0; // Normalize value for color intensity
chart
.draw_series(std::iter::once(Rectangle::new(
[
(x.clone() as i32, y.clone() as i32),
((x + 1).try_into().unwrap(), (y + 1).try_into().unwrap())
],
ShapeStyle::from(&HSLColor(0.6, 1.0, 1.0 - intensity)).filled(),
)))
.unwrap();
}
}
root.present().unwrap();
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let learning_rates = vec![0.1, 0.5, 0.9];
let discount_factors = vec![0.5, 0.9, 1.0];
let mut results = Vec::new();
for &alpha in &learning_rates {
for &gamma in &discount_factors {
let value_function = td_zero(&grid_world, episodes, alpha, gamma);
results.push((alpha, gamma, value_function));
}
}
visualize_results(&results, grid_world.size, "output.png");
}
The program simulates a 4x4 GridWorld environment where an agent learns the value of states using the TD(0) algorithm. The learning process involves iteratively updating the value function for each state based on the temporal difference error calculated during episodes. The code systematically varies $\alpha$ (learning rate) and $\gamma$ (discount factor), generating value functions for all combinations of these parameters. It then visualizes the results using the plotters crate, where each grid cell’s color intensity represents the learned value of that state. These visualizations are arranged into a single 3x3 image, with captions identifying the corresponding parameter values.
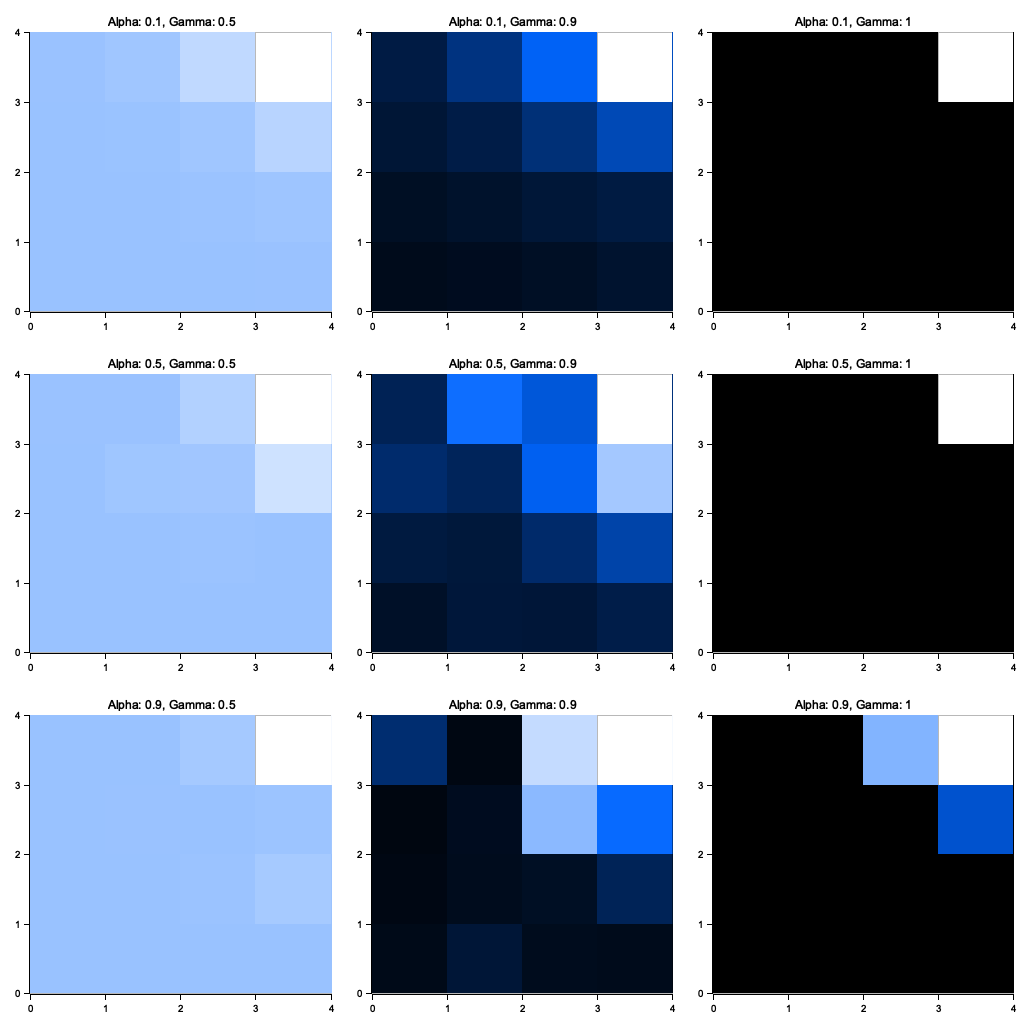
Figure 3: Plotters visualization of the experiment.
The combined visualization illustrates the interplay between $\alpha$ and $\gamma$ in the TD(0) learning process. Higher $\alpha$ values generally lead to faster convergence but may introduce instability, resulting in noisier value functions. Conversely, lower $\alpha$ values yield slower yet smoother convergence. Similarly, higher $\gamma$ values prioritize long-term rewards, often producing more pronounced value gradients, whereas lower $\gamma$ values focus on immediate rewards, leading to less distinct value differentiation. The visualizations highlight these trade-offs, allowing users to select parameter combinations that balance convergence speed and stability for their specific use case.
By integrating theoretical concepts with practical Rust implementations, this section provides a comprehensive introduction to Temporal-Difference learning. The examples illustrate the versatility and efficiency of TD methods, offering readers valuable insights into real-time value updates in reinforcement learning tasks.
6.2. SARSA: On-Policy TD Control
SARSA (State-Action-Reward-State-Action) emerged as a refinement in the reinforcement learning paradigm, specifically addressing the need for on-policy methods that integrate exploration strategies effectively. While its foundational principles align with Temporal-Difference (TD) learning, SARSA’s origins are distinct in its focus on learning policies that are consistent with the agent’s actual behavior.
During the late 1980s and early 1990s, research in reinforcement learning was dominated by efforts to develop model-free algorithms that could balance learning efficiency and adaptability. While off-policy methods like Q-learning, introduced by Chris Watkins in 1989, demonstrated the potential for learning optimal policies by decoupling the learning and behavior policies, they also highlighted challenges in scenarios where exploration was crucial. Off-policy approaches often prioritized exploitation, making it difficult to integrate strategies like epsilon-greedy exploration without destabilizing the learning process.
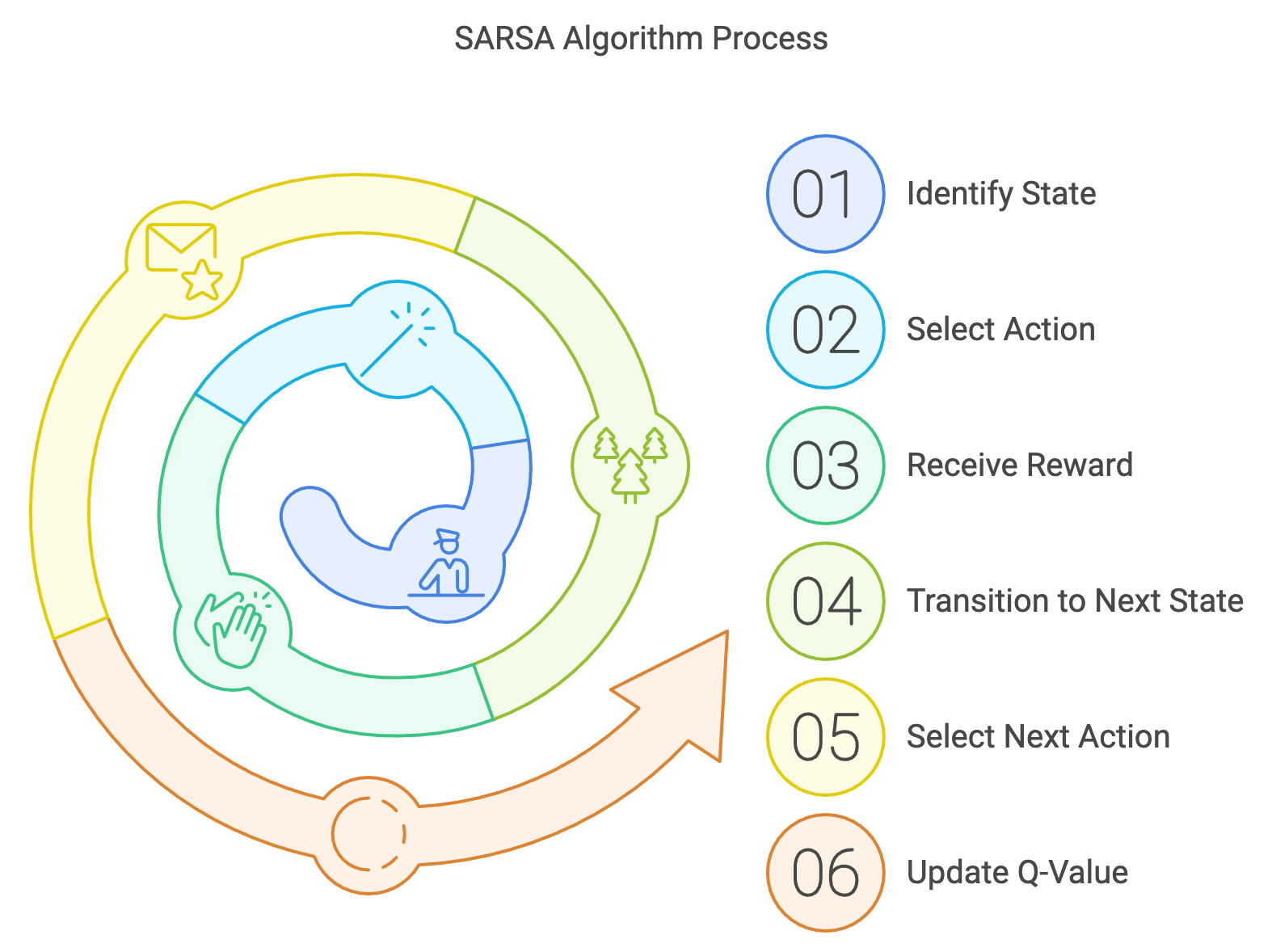
Figure 4: How SARSA algorithm works.
SARSA was introduced in the mid-1990s as an on-policy alternative that retained the agent's behavior policy as the basis for learning. This approach ensured that the updates to the action-value function $Q(s, a)$ were directly tied to the actions actually taken by the agent, rather than hypothetical optimal actions. By doing so, SARSA provided a natural way to incorporate exploration strategies into the learning process, offering a more stable framework for policy improvement in uncertain environments.
The name SARSA reflects the sequence of elements—state, action, reward, next state, and next action—used in its update rule, emphasizing the continuity between the agent’s actions and its learning process. This method became particularly appealing for scenarios requiring safe or controlled exploration, such as navigation tasks, where the agent's behavior policy must align closely with its learned policy.
SARSA's introduction expanded the reinforcement learning toolkit, providing a method that complemented existing algorithms by focusing on the interplay between exploration and policy consistency. It remains a widely studied and applied algorithm, valued for its simplicity and effectiveness in tasks where alignment between learning and behavior is essential.
SARSA is a fundamental on-policy Temporal-Difference (TD) control algorithm in reinforcement learning. Unlike off-policy methods such as Q-learning, SARSA learns the action-value function $Q(s, a)$ based on the actions that the current policy actually takes, rather than the optimal actions. This approach ensures that SARSA remains consistent with the policy being followed, allowing for natural integration of exploration strategies such as epsilon-greedy.
The SARSA update rule is mathematically expressed as:
$$ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ R_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t) \right], $$
where:
$\alpha$ is the learning rate,
$\gamma$ is the discount factor,
$Q(s_t, a_t)$ is the estimated value of taking action $a_t$ in state $s_t$,
$R_{t+1}$ is the reward for transitioning to the next state $s_{t+1}$,
$Q(s_{t+1}, a_{t+1})$ is the value of the next state-action pair under the current policy.
An intuitive analogy for SARSA is navigating through a maze. Imagine you’re trying to find the exit, but you can only update your strategy based on the paths you actually take (even if they are suboptimal), rather than assuming you always make the best move.
SARSA’s update rule captures the essence of on-policy learning. The TD error in SARSA depends on the next action $a_{t+1}$ selected by the policy. This dependence ensures that SARSA takes into account the exploration strategy defined by the policy, such as epsilon-greedy. This makes SARSA particularly suitable for real-world scenarios where agents must balance exploration (trying out new actions) and exploitation (optimizing for rewards).
The exploration-exploitation trade-off is built into SARSA because the agent updates its action-value estimates based on actual, potentially exploratory actions. This ensures that even suboptimal actions contribute to learning, providing a comprehensive understanding of the environment.
SARSA converges to the optimal policy under specific conditions:
Exploration: The policy must explore all state-action pairs infinitely often. This can be achieved using an epsilon-greedy policy, where $\epsilon$-randomness ensures exploration.
Learning Rate: The learning rate $\alpha$ must satisfy the conditions $\sum_{t=1}^\infty \alpha_t = \infty$ and $\sum_{t=1}^\infty \alpha_t^2 < \infty$ to guarantee convergence.
Stationary Environment: The environment must not change during the learning process.
These conditions ensure that SARSA iteratively improves the policy while avoiding premature convergence or oscillations.
The following implementation demonstrates SARSA applied to a simple grid world environment. The agent learns to navigate the grid using an epsilon-greedy policy, balancing exploration and exploitation. The implementation explores how varying epsilon values affect the learning process. SARSA is an on-policy reinforcement learning algorithm used to estimate the optimal action-value function for a given environment. Unlike off-policy methods like Q-learning, SARSA follows the agent's current policy, updating Q-values based on the action it actually takes. This approach incorporates the interaction between the agent's exploration and exploitation strategies, making SARSA particularly well-suited for environments where the exploration behavior is critical to learning.
use std::collections::HashMap;
use rand::Rng;
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 }; // Goal state has no penalty
(next_state, reward)
}
}
// SARSA algorithm
fn sarsa(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
let mut action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
while state != grid_world.goal_state {
let (next_state, reward) = grid_world.step(state, action);
let next_action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(next_state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(next_state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
let next_q = *q_values.get(&(next_state, next_action)).unwrap_or(&0.0);
// Update Q-value using SARSA update rule
let td_error = reward + gamma * next_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
action = next_action;
}
}
q_values
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
let epsilon = 0.1;
let q_values = sarsa(&grid_world, episodes, alpha, gamma, epsilon);
println!("Learned Q-Values: {:?}", q_values);
}
SARSA operates by iteratively updating Q-values using the tuple $(s, a, r, s', a')$, which represents the current state $s$, chosen action aaa, received reward $r$, next state $s'$, and the next action $a'$. The algorithm begins in an initial state, selects an action using an $\epsilon$-greedy policy, and observes the subsequent state and reward. The Q-value is then updated using the temporal difference (TD) error, calculated as the difference between the current Q-value and the reward plus the discounted Q-value of the next state-action pair. By repeating this process over multiple episodes, SARSA learns a policy that balances exploration (via random actions) and exploitation (via the greedy policy), gradually converging to the optimal Q-values.
The modified code extends the initial SARSA implementation by introducing an experiment to analyze the impact of varying $\epsilon$ values on the learning process. While the original code used a fixed $\epsilon$ value, this version systematically evaluates multiple values ranging from 0.1 to 0.9, representing different balances between exploration and exploitation. The results are visualized using heatmaps for each $\epsilon$, allowing a comparative analysis of the learned Q-values across the grid world for varying exploration strategies.
use std::collections::HashMap;
use plotters::prelude::*;
use rand::Rng;
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 }; // Goal state has no penalty
(next_state, reward)
}
}
// SARSA algorithm
fn sarsa(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
let mut action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
while state != grid_world.goal_state {
let (next_state, reward) = grid_world.step(state, action);
let next_action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(next_state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(next_state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
let next_q = *q_values.get(&(next_state, next_action)).unwrap_or(&0.0);
// Update Q-value using SARSA update rule
let td_error = reward + gamma * next_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
action = next_action;
}
}
q_values
}
// Visualize the impact of varying epsilon
fn visualize_epsilon_impact(
epsilons: Vec<f64>,
grid_size: usize,
output_path: &str,
results: Vec<(f64, HashMap<((usize, usize), usize), f64>)>,
) {
let root = BitMapBackend::new(output_path, (1024, 1024)).into_drawing_area();
root.fill(&WHITE).unwrap();
let areas = root.split_evenly((epsilons.len(), 1)); // One row for each epsilon value
for (area, (epsilon, q_values)) in areas.iter().zip(results.iter()) {
let mut chart = ChartBuilder::on(area)
.caption(format!("Epsilon: {}", epsilon), ("sans-serif", 15))
.margin(10)
.x_label_area_size(20)
.y_label_area_size(20)
.build_cartesian_2d(0..grid_size as i32, 0..grid_size as i32)
.unwrap();
chart.configure_mesh().draw().unwrap();
for (((x, y), _), value) in q_values.iter() {
let intensity = (*value).max(-10.0).min(0.0) / -10.0; // Normalize value for color intensity
chart
.draw_series(std::iter::once(Rectangle::new(
// Convert usize to i32 using try_into().unwrap() to handle potential conversion
[(*x as i32, *y as i32), ((*x + 1).try_into().unwrap(), (*y + 1).try_into().unwrap())],
ShapeStyle::from(&HSLColor(0.6, 1.0, 1.0 - intensity)).filled(),
)))
.unwrap();
}
}
root.present().unwrap();
println!("Visualization completed. Saved to {}", output_path);
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
let epsilons = vec![0.1, 0.3, 0.5, 0.7, 0.9];
let mut results = Vec::new();
for &epsilon in &epsilons {
println!("Running SARSA for Epsilon: {}", epsilon);
let q_values = sarsa(&grid_world, episodes, alpha, gamma, epsilon);
results.push((epsilon, q_values));
}
visualize_epsilon_impact(epsilons, grid_world.size, "epsilon_impact.png", results);
}
The visualization highlights the trade-off between exploration and exploitation driven by $\epsilon$. At low $\epsilon$ values (e.g., 0.1), the agent primarily exploits its current knowledge, leading to quicker convergence but potentially suboptimal Q-values due to limited exploration. In contrast, higher $\epsilon$ values (e.g., 0.7 or 0.9) promote extensive exploration, enabling the agent to discover more states and actions, resulting in more robust Q-values but at the cost of slower convergence. These findings underscore the importance of choosing an appropriate $\epsilon$ value to balance learning efficiency and state-action coverage in reinforcement learning.
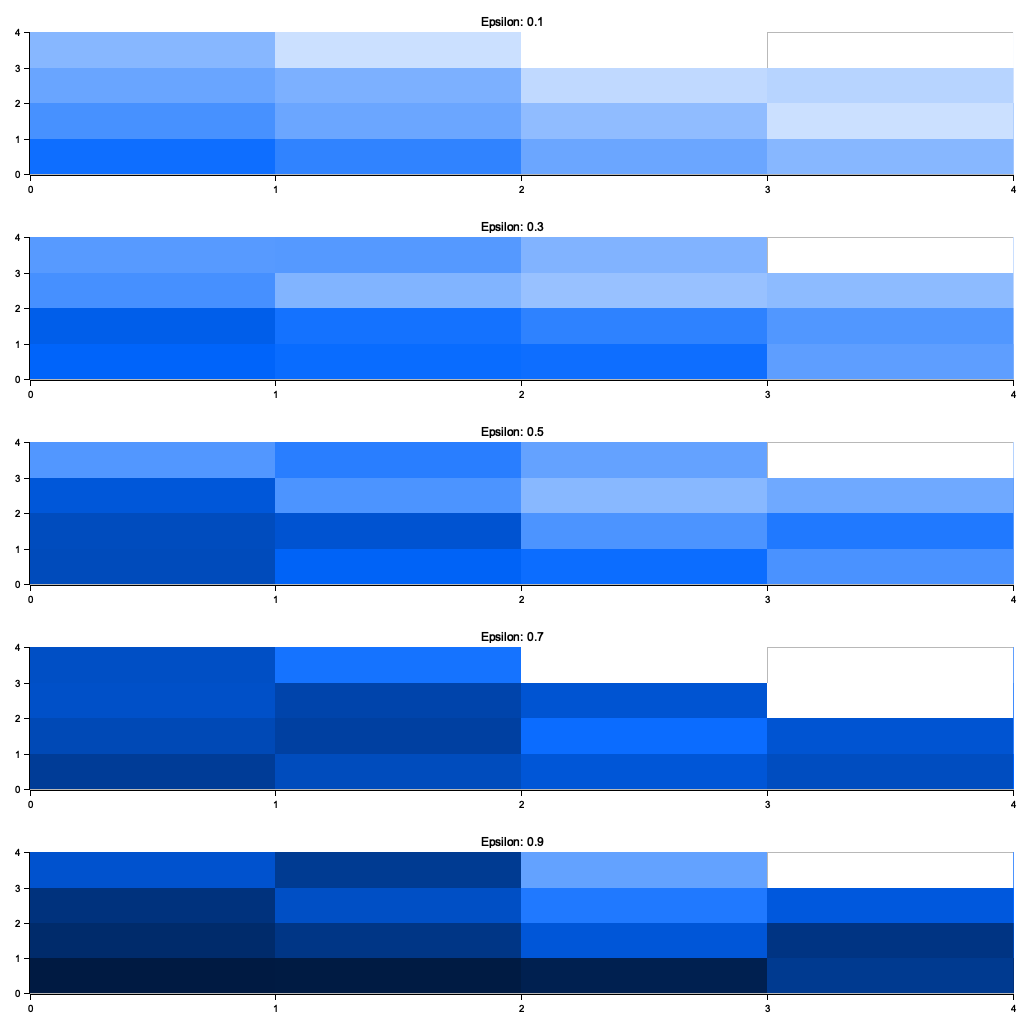
Figure 5: Plotters visualization of varying the value of $\epsilon$.
The next experiment compares the SARSA and Q-learning algorithms, focusing on their convergence speed and stability in a 4x4 grid world environment. Both algorithms are tasked with learning the Q-values for state-action pairs over 1,000 episodes, using identical learning rate ($\alpha = 0.1$), discount factor ($\gamma = 0.9$), and exploration probability ($\epsilon = 0.1$). The key goal is to highlight the differences between SARSA's on-policy updates, which depend on the agent's actual behavior, and Q-learning's off-policy updates, which rely on optimal action assumptions for the next state.
use std::collections::HashMap;
use rand::Rng;
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 }; // Goal state has no penalty
(next_state, reward)
}
}
// SARSA algorithm
fn sarsa(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
let mut action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
while state != grid_world.goal_state {
let (next_state, reward) = grid_world.step(state, action);
let next_action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(next_state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(next_state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
let next_q = *q_values.get(&(next_state, next_action)).unwrap_or(&0.0);
// Update Q-value using SARSA update rule
let td_error = reward + gamma * next_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
action = next_action;
}
}
q_values
}
// Q-learning algorithm
fn q_learning(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
while state != grid_world.goal_state {
let action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let (next_state, reward) = grid_world.step(state, action);
let next_max_q = (0..4)
.map(|a| *q_values.get(&(next_state, a)).unwrap_or(&0.0))
.fold(f64::MIN, f64::max); // Max Q-value for the next state
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
// Update Q-value using Q-learning update rule
let td_error = reward + gamma * next_max_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
}
}
q_values
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
let epsilon = 0.1;
println!("Running SARSA...");
let sarsa_q_values = sarsa(&grid_world, episodes, alpha, gamma, epsilon);
println!("SARSA Q-Values: {:?}", sarsa_q_values);
println!("Running Q-Learning...");
let q_learning_q_values = q_learning(&grid_world, episodes, alpha, gamma, epsilon);
println!("Q-Learning Q-Values: {:?}", q_learning_q_values);
println!("Comparison completed.");
}
The code implements both SARSA and Q-learning as separate functions, each updating Q-values based on their respective update rules. SARSA computes updates using the reward and the Q-value of the next state-action pair ($(s', a')$) based on the agent's chosen policy, promoting stability by aligning updates with the agent's exploration strategy. In contrast, Q-learning updates Q-values using the maximum action-value for the next state ($(s', \max_a Q(s', a))$), emphasizing optimality and potentially faster convergence. Both algorithms interact with a shared grid world environment, taking random or greedy actions based on an $\epsilon$-greedy policy.
The results demonstrate notable differences between the algorithms. SARSA tends to converge more steadily as its updates align with the agent's actual policy, making it robust in environments with significant exploration. However, it may take longer to converge fully to the optimal Q-values. On the other hand, Q-learning often converges faster by directly targeting optimal action-values, but this can lead to instability, especially if the exploration probability ($\epsilon$) is high, as it might overestimate action values. These differences emphasize the trade-off between stability and convergence speed when selecting between on-policy and off-policy methods.
By combining theoretical insights with practical Rust implementations, this section provides readers with a comprehensive understanding of SARSA, its applications, and its strengths as an on-policy TD control method. The examples and experiments offer hands-on experience with one of the most widely used algorithms in reinforcement learning.
6.3. Q-Learning: Off-Policy TD Control
Q-Learning, introduced by Chris Watkins in 1989, marked a significant milestone in the evolution of reinforcement learning algorithms. Its development was driven by the need for methods that could learn optimal policies in environments where explicit models were unavailable or computationally infeasible to use. At the time, most reinforcement learning methods were either model-based, relying on dynamic programming techniques, or on-policy, requiring the agent's learned policy to align with its behavior policy.
Watkins's key insight was to decouple the learning process from the agent’s behavior policy, giving rise to the concept of off-policy learning. This innovation addressed a critical limitation of on-policy methods like SARSA, which updated value functions based only on the actions taken by the current policy. By allowing the action-value function $Q(s, a)$ to be updated based on the optimal action, regardless of the agent’s exploratory behavior, Q-Learning enabled agents to explore their environment freely while still learning toward the optimal policy.
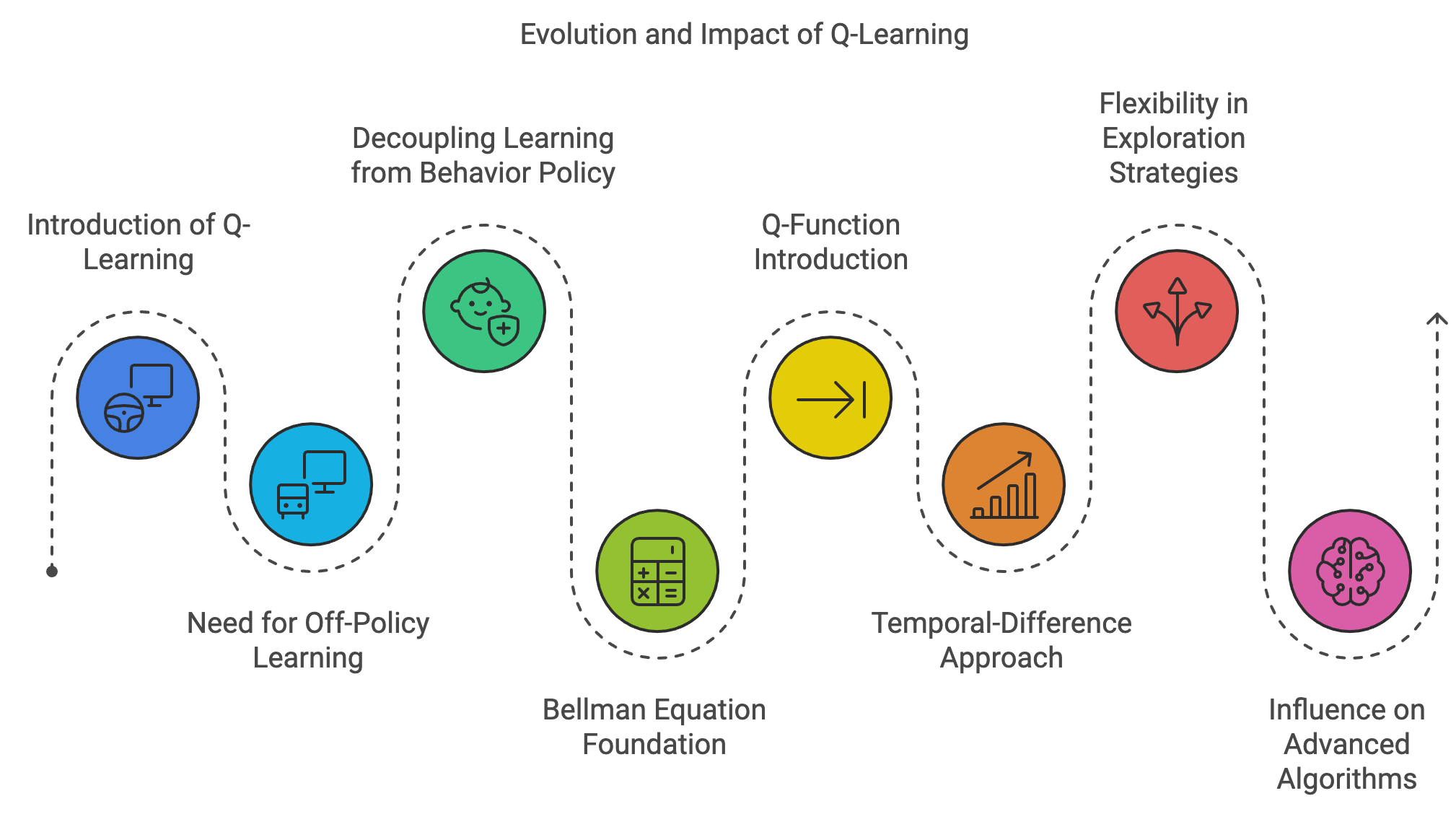
Figure 6: The evolution and impact of Q-learning method.
The algorithm’s foundation lies in the Bellman equation, which provides a recursive relationship for computing value functions. Watkins extended this idea by introducing the Q-function, representing the expected utility of taking an action $a$ in a state $s$ and following the optimal policy thereafter. The Q-Learning update rule incrementally refines the Q-function using a Temporal-Difference (TD) approach, making it both computationally efficient and robust to stochastic environments.
Q-Learning’s off-policy nature became a pivotal feature, allowing agents to explore using strategies like epsilon-greedy or Boltzmann exploration while still converging to the optimal policy. This flexibility made Q-Learning a versatile and powerful algorithm, particularly well-suited for complex, dynamic environments where exploration is critical.
Since its introduction, Q-Learning has influenced a wide range of applications and advancements in reinforcement learning, from robotics to game playing. It served as a foundational building block for more advanced algorithms, such as Deep Q-Networks (DQNs), which combine Q-Learning with deep learning to handle high-dimensional state spaces. Today, Q-Learning remains a cornerstone of reinforcement learning, celebrated for its simplicity, robustness, and enduring impact on the field.
Till now, Q-Learning is one of the most influential algorithms in reinforcement learning, known for its ability to learn the optimal policy while following any behavior policy. Unlike on-policy methods such as SARSA, Q-Learning is an off-policy Temporal-Difference (TD) control algorithm. This means it updates its action-value function $Q(s, a)$ based on the optimal action for the next state, rather than the action actually taken by the agent. This property allows Q-Learning to converge to the optimal policy, even when the agent explores the environment using a suboptimal or exploratory behavior policy.
The update rule for Q-Learning is defined as:
$$ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ R_{t+1} + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t) \right], $$
where:
$\alpha$ is the learning rate, controlling the step size of updates,
$\gamma$ is the discount factor, balancing the importance of immediate versus future rewards,
$R_{t+1}$ is the reward obtained for transitioning to state $s_{t+1}$,
$\max_{a'} Q(s_{t+1}, a')$ represents the value of the optimal action in the next state.
An intuitive analogy for Q-Learning is optimizing a travel route by always considering the shortest possible path from your current location to the destination, even if your current path involves detours for exploration.
On-Policy vs. Off-Policy Learning: In on-policy methods like SARSA, the action-value function is updated based on the action actually taken, making the updates consistent with the policy being followed. In contrast, Q-Learning separates the behavior policy (used for exploration) from the target policy (used for learning). The target policy is implicitly defined as the greedy policy that always selects the action with the highest Q-value.
Role of the Max Operator: The max operator in Q-Learning ensures that the agent always considers the best possible future reward when updating its Q-values. This allows the algorithm to converge to the optimal policy by prioritizing the most rewarding actions in the long run.
Impact of Learning Rate and Discount Factor: The learning rate α\\alphaα determines how much the agent updates its Q-values based on new information, while the discount factor $\gamma$ controls the agent’s emphasis on future rewards. High $\alpha$ values can lead to rapid but unstable learning, while low $\alpha$ values may result in slow convergence. Similarly, a high $\gamma$ encourages long-term planning, while a low $\gamma$ prioritizes immediate rewards.
This code implements a Q-learning algorithm to solve a 4x4 grid world environment, where the objective is to find an optimal policy for reaching a goal state at the bottom-right corner from the top-left corner. The algorithm employs a reinforcement learning approach to iteratively update action-value (Q) estimates for each state-action pair, allowing the agent to balance exploration and exploitation through an $\epsilon$-greedy policy. The grid world rewards the agent with -1 for every step until it reaches the goal, incentivizing shorter paths.
use std::collections::HashMap;
use rand::Rng;
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 }; // Goal state has no penalty
(next_state, reward)
}
}
// Q-Learning algorithm
fn q_learning(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
while state != grid_world.goal_state {
let action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let (next_state, reward) = grid_world.step(state, action);
let max_next_q = (0..4)
.map(|a| *q_values.get(&(next_state, a)).unwrap_or(&0.0))
.fold(f64::NEG_INFINITY, f64::max);
// Update Q-value using Q-Learning update rule
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
let td_error = reward + gamma * max_next_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
}
}
q_values
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
let epsilon = 0.1;
let q_values = q_learning(&grid_world, episodes, alpha, gamma, epsilon);
println!("Learned Q-Values: {:?}", q_values);
}
The q_learning function initializes a Q-table as a hash map and simulates the agent’s interaction with the grid world over multiple episodes. For each episode, the agent begins at the top-left corner and selects actions using an $\epsilon$-greedy policy—random actions with probability $\epsilon$ (exploration) or the action with the highest Q-value for the current state (exploitation). The agent receives a reward and transitions to the next state, where the maximum Q-value of the next state $\max_a Q(s', a)$ is used to calculate the temporal difference (TD) error. The Q-value for the current state-action pair is updated using this error and a learning rate ($\alpha$). This process repeats until the agent reaches the goal state, and the algorithm iteratively improves the policy as it learns the optimal path to the goal.
Compared to the initial version, the code below introduces an experiment to analyze how varying the learning rate ($\alpha$) and discount factor ($\gamma$) affects the Q-learning process in a 4x4 grid world. By iterating over multiple combinations of $\alpha$ and $\gamma$, the code evaluates their impact on the convergence of Q-values. The results are visualized using heatmaps, where each cell represents the Q-values learned for a specific $\alpha, \gamma$ combination, providing an intuitive way to understand their influence on the learning dynamics.
use std::collections::HashMap;
use plotters::prelude::*;
use rand::Rng;
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 }; // Goal state has no penalty
(next_state, reward)
}
}
// Q-Learning algorithm
fn q_learning(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
while state != grid_world.goal_state {
let action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let (next_state, reward) = grid_world.step(state, action);
let max_next_q = (0..4)
.map(|a| *q_values.get(&(next_state, a)).unwrap_or(&0.0))
.fold(f64::NEG_INFINITY, f64::max);
// Update Q-value using Q-Learning update rule
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
let td_error = reward + gamma * max_next_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
}
}
q_values
}
// Visualize the results for varying alpha and gamma
fn visualize_alpha_gamma_impact(
alphas: Vec<f64>,
gammas: Vec<f64>,
grid_size: usize,
output_path: &str,
results: Vec<(f64, f64, HashMap<((usize, usize), usize), f64>)>,
) {
let root = BitMapBackend::new(output_path, (1024, 1024)).into_drawing_area();
root.fill(&WHITE).unwrap();
let areas = root.split_evenly((alphas.len(), gammas.len())); // Each cell corresponds to an alpha-gamma combination
for (area, (alpha, gamma, q_values)) in areas.iter().zip(results.iter()) {
let mut chart = ChartBuilder::on(area)
.caption(format!("Alpha: {}, Gamma: {}", alpha, gamma), ("sans-serif", 15))
.margin(10)
.x_label_area_size(20)
.y_label_area_size(20)
.build_cartesian_2d(0..grid_size as i32, 0..grid_size as i32)
.unwrap();
chart.configure_mesh().draw().unwrap();
for (((x, y), _), value) in q_values.iter() {
let intensity = (*value).max(-10.0).min(0.0) / -10.0; // Normalize value for color intensity
chart
.draw_series(std::iter::once(Rectangle::new(
[(*x as i32, *y as i32), ((*x + 1) as i32, (*y + 1) as i32)],
ShapeStyle::from(&HSLColor(0.6, 1.0, 1.0 - intensity)).filled(),
)))
.unwrap();
}
}
root.present().unwrap();
println!("Visualization completed. Saved to {}", output_path);
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let epsilon = 0.1;
let alphas = vec![0.1, 0.5, 0.9];
let gammas = vec![0.5, 0.9, 1.0];
let mut results = Vec::new();
for &alpha in &alphas {
for &gamma in &gammas {
println!("Running Q-Learning for Alpha: {}, Gamma: {}", alpha, gamma);
let q_values = q_learning(&grid_world, episodes, alpha, gamma, epsilon);
results.push((alpha, gamma, q_values));
}
}
visualize_alpha_gamma_impact(alphas, gammas, grid_world.size, "alpha_gamma_impact.png", results);
}
The Q-learning function iteratively updates Q-values for state-action pairs based on the temporal difference (TD) error calculated using rewards and the maximum Q-value of the next state. The main experiment varies $\alpha$ and $\gamma$, running the Q-learning algorithm for each combination across 1,000 episodes. The learned Q-values are then stored for visualization. The visualize_alpha_gamma_impact function generates heatmaps for each combination of parameters, where the color intensity represents the normalized Q-values. The heatmaps are arranged in a grid layout, with rows corresponding to different $\alpha$ values and columns to different $\gamma$ values.
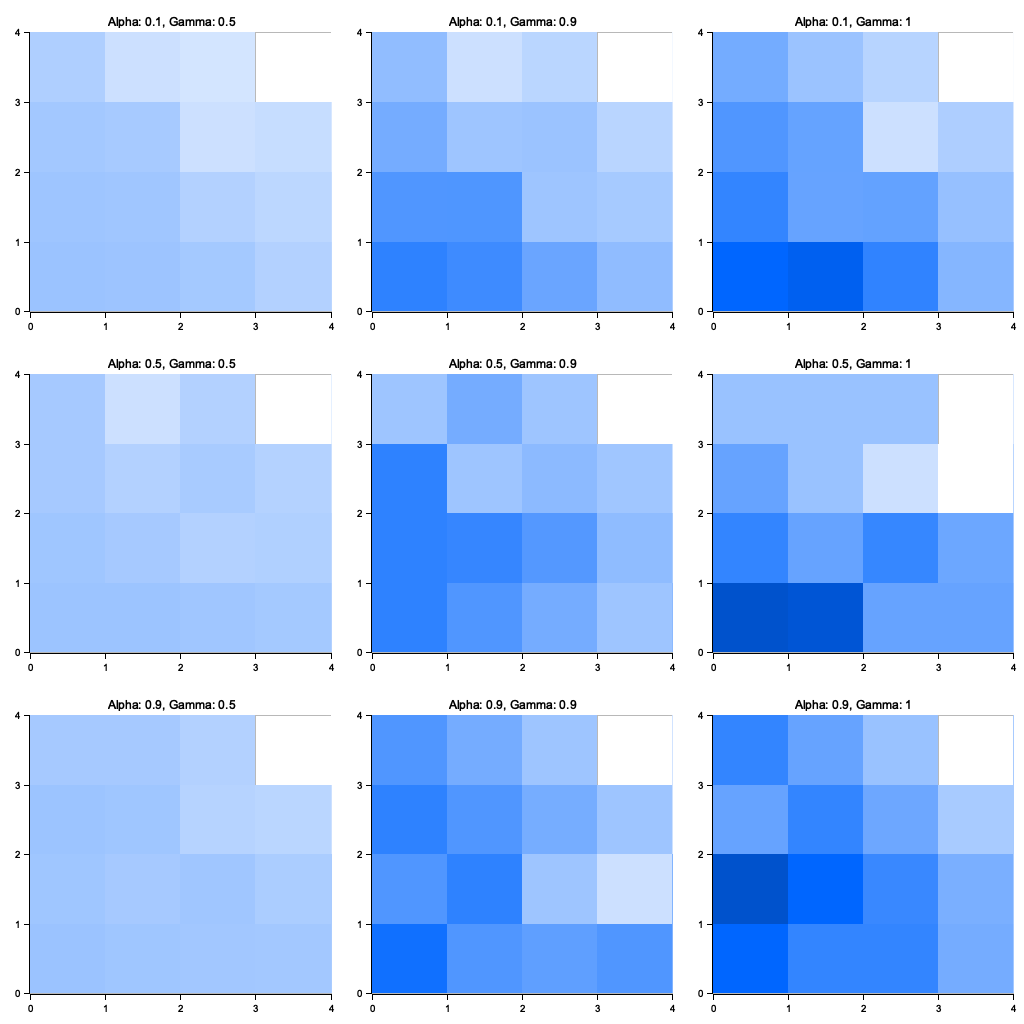
Figure 7: Plotters visualization of the experiment.
The visualizations reveal the trade-offs between learning rate and discount factor in the Q-learning process. Higher $\alpha$ values (e.g., 0.9) lead to faster updates and quicker convergence but can introduce instability, as evident from noisier heatmaps. Lower $\alpha$ values (e.g., 0.1) result in smoother Q-value updates but slower learning. Higher $\gamma$ values (e.g., 1.0) emphasize long-term rewards, creating distinct value gradients that prioritize reaching the goal. Lower $\gamma$ values (e.g., 0.5) focus on immediate rewards, leading to less pronounced value differentiation. These findings highlight the importance of tuning $\alpha$ and $\gamma$ for achieving a balance between learning speed, stability, and prioritization of rewards.
Next experiment compares the performance of Q-Learning (off-policy) and SARSA (on-policy) in a shared 4x4 grid world environment. Both algorithms aim to learn optimal policies for reaching a goal state from a starting state by updating Q-values for state-action pairs over 1,000 episodes. While Q-Learning prioritizes selecting actions based on the maximum future reward (off-policy), SARSA updates Q-values based on the actions actually taken (on-policy), offering a more realistic evaluation of the agent’s policy. The experiment highlights differences in their learning dynamics, convergence, and stability.
use std::collections::HashMap;
use rand::Rng;
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 0.0 } else { -1.0 }; // Goal state has no penalty
(next_state, reward)
}
}
// Q-Learning algorithm
fn q_learning(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0);
while state != grid_world.goal_state {
let action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let (next_state, reward) = grid_world.step(state, action);
let max_next_q = (0..4)
.map(|a| *q_values.get(&(next_state, a)).unwrap_or(&0.0))
.fold(f64::NEG_INFINITY, f64::max);
// Update Q-value using Q-Learning update rule
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
let td_error = reward + gamma * max_next_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
}
}
q_values
}
// SARSA algorithm
fn sarsa(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
epsilon: f64,
) -> HashMap<((usize, usize), usize), f64> {
let mut q_values: HashMap<((usize, usize), usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = (0, 0);
let mut action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
while state != grid_world.goal_state {
let (next_state, reward) = grid_world.step(state, action);
let next_action = if rng.gen::<f64>() < epsilon {
rng.gen_range(0..4) // Random action (exploration)
} else {
(0..4)
.max_by(|&a, &b| {
q_values
.get(&(next_state, a))
.unwrap_or(&0.0)
.partial_cmp(q_values.get(&(next_state, b)).unwrap_or(&0.0))
.unwrap()
})
.unwrap_or(0) // Greedy action (exploitation)
};
let current_q = *q_values.get(&(state, action)).unwrap_or(&0.0);
let next_q = *q_values.get(&(next_state, next_action)).unwrap_or(&0.0);
// Update Q-value using SARSA update rule
let td_error = reward + gamma * next_q - current_q;
q_values
.entry((state, action))
.and_modify(|q| *q += alpha * td_error)
.or_insert(alpha * td_error);
state = next_state;
action = next_action;
}
}
q_values
}
fn main() {
let grid_world = GridWorld {
size: 4,
goal_state: (3, 3),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
let epsilon = 0.1;
println!("Running Q-Learning...");
let q_values = q_learning(&grid_world, episodes, alpha, gamma, epsilon);
println!("Q-Learning Q-Values: {:?}", q_values);
println!("Running SARSA...");
let sarsa_q_values = sarsa(&grid_world, episodes, alpha, gamma, epsilon);
println!("SARSA Q-Values: {:?}", sarsa_q_values);
println!("Comparison completed.");
}
The code implements both Q-Learning and SARSA algorithms, using the same grid world and hyperparameters for fair comparison. Q-Learning updates Q-values using the maximum Q-value of the next state ($\max_a Q(s', a)$), focusing on an idealized optimal policy. SARSA, on the other hand, updates Q-values based on the next action chosen by the agent ($Q(s', a')$), reflecting the agent’s actual policy during learning. Both algorithms use an $\epsilon$-greedy policy for action selection, balancing exploration and exploitation. The Q-values learned by each algorithm are printed for comparative analysis.
The results demonstrate the trade-offs between the two approaches. Q-Learning often converges faster due to its focus on optimal actions, but it can exhibit instability in environments with significant exploration. SARSA, being on-policy, provides more stable learning as it updates Q-values based on the agent’s actual actions, aligning updates with the current exploration strategy. However, this can lead to slower convergence compared to Q-Learning. These insights highlight the importance of choosing the appropriate algorithm based on the stability requirements and the exploration-exploitation balance in a given application.
By integrating theoretical concepts with practical Rust implementations, this section offers a comprehensive understanding of Q-Learning, its strengths as an off-policy TD control method, and its applications in reinforcement learning tasks. The experiments provide hands-on insights into the algorithm’s behavior under different conditions, equipping readers with the tools to apply Q-Learning effectively in real-world scenarios.
6.4. n-Step TD Methods
The development of n-step Temporal Difference (TD) methods represents a natural evolution in reinforcement learning, aimed at unifying and generalizing the strengths of existing approaches like TD(0) and Monte Carlo methods. These methods emerged as researchers sought to balance the trade-offs between computational efficiency and the quality of value estimates.
TD(0), introduced in the foundational work on Temporal Difference learning by Richard Sutton in 1988, updates value estimates incrementally using the immediate reward and a bootstrap estimate of the next state’s value. While computationally efficient and suitable for real-time learning, TD(0) relies heavily on short-term transitions, which can sometimes limit its accuracy in estimating long-term returns.
Monte Carlo methods, on the other hand, estimate value functions by averaging returns over complete episodes. While these methods are unbiased and incorporate long-term outcomes, they require waiting until an episode concludes before updating value estimates. This can be computationally expensive and impractical for tasks involving long or continuous episodes.
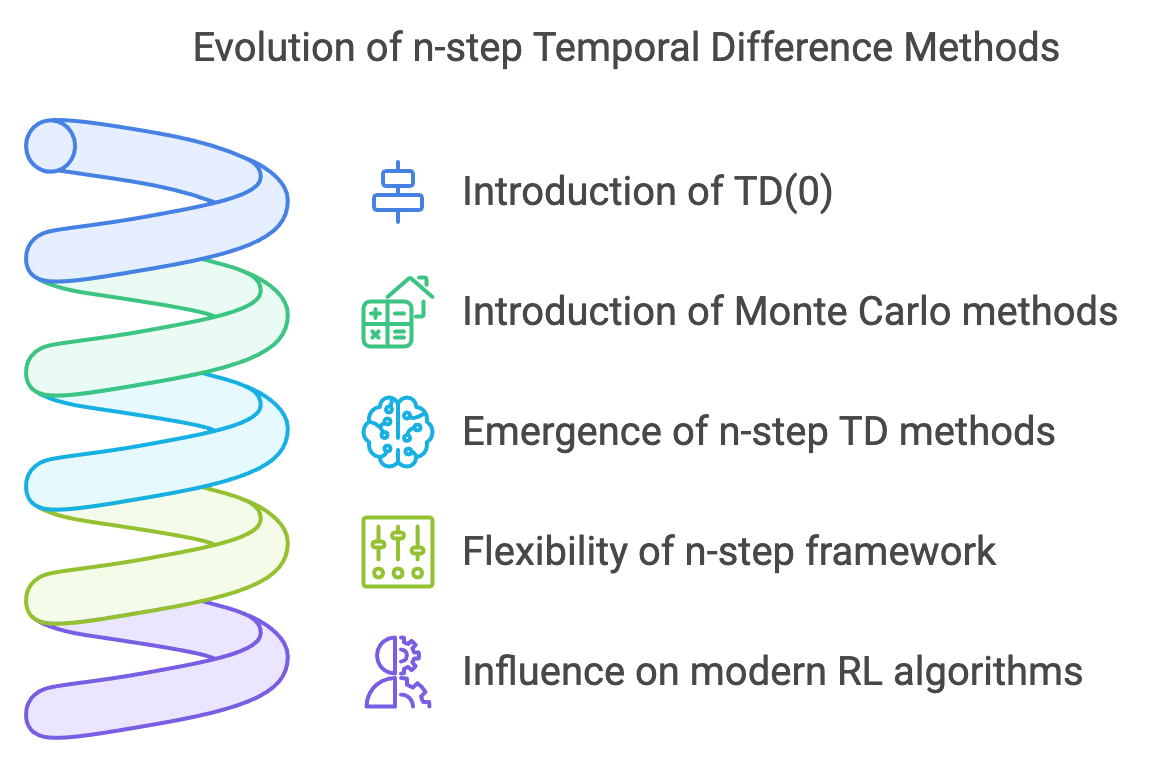
Figure 8: The evolution of n-step TD methods.
The introduction of n-step TD methods aimed to bridge this divide by incorporating information from multiple steps into the update process. By using an $n$-step return that sums rewards over $n$ transitions and bootstraps the value estimate after $n$ steps, these methods allow for greater flexibility. For small $n$, n-step TD resembles TD(0), emphasizing short-term updates. As $n$ increases, the method approaches Monte Carlo techniques, capturing more of the long-term return.
The flexibility of the n-step framework made it particularly appealing for reinforcement learning practitioners, as it offered a tunable parameter $n$ to balance bias and variance in value estimates. This framework also paved the way for more advanced algorithms like TD(λ), which generalizes n-step TD methods by averaging over all possible step lengths weighted by a decay parameter $\lambda$.
Since their introduction, n-step TD methods have been instrumental in advancing reinforcement learning, particularly in scenarios where episodic learning is impractical or where a balance between short-term and long-term value estimates is critical. Their impact continues to resonate in modern RL algorithms, influencing the development of multi-step methods used in deep reinforcement learning frameworks.
n-Step Temporal Difference (TD) methods extend the classical TD(0) approach by considering the cumulative return over multiple steps before updating the value function. This technique bridges the gap between TD(0), which updates based on immediate transitions, and Monte Carlo methods, which rely on entire episodes. The n-step framework introduces a flexible spectrum of algorithms, allowing reinforcement learning practitioners to balance computational efficiency and learning accuracy.
The essence of n-Step TD lies in the n-step return, a cumulative reward that includes $n$ steps of observed rewards followed by a bootstrapped estimate from the value function. The n-step return for state $s_t$ is defined as:
$$ G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n}), $$
where:
$R_{t+1}, R_{t+2}, \dots, R_{t+n}$ are rewards for the next $n$ steps,
$\gamma$ is the discount factor,
$V(S_{t+n})$ is the value of the state after $n$ steps.
The value function is updated as:
$$ V(S_t) \leftarrow V(S_t) + \alpha \left( G_t^{(n)} - V(S_t) \right), $$
where $\alpha$ is the learning rate.
By choosing different values of nnn, this method provides a spectrum of algorithms:
$n = 1$: The method becomes TD(0), relying entirely on immediate transitions.
$n = \infty$: The method approximates Monte Carlo, using complete episodes for updates.
The parameter $n$ is pivotal in determining the trade-off between bias and variance in the learning process:
Smaller values of $n$: Emphasize immediate rewards, resulting in faster updates but potentially introducing bias due to reliance on short-term information.
Larger values of $n$: Incorporate more future rewards, reducing bias but increasing variance due to noise in longer-term returns.
An analogy for $n$ is deciding the granularity of planning a vacation. Using $n = 1$ is like planning just the next activity, ensuring quick decisions but possibly missing long-term opportunities. Using $n = \infty$ is like planning the entire trip, which ensures a well-thought-out journey but requires extensive effort and may involve unforeseen uncertainties.
The n-Step TD methods and eligibility traces are closely related. Eligibility traces generalize the n-step concept by assigning decaying weights to all prior states based on their recency, effectively combining the strengths of various n-step methods into a unified framework. This connection highlights the flexibility of TD methods in addressing diverse reinforcement learning challenges.
The following implementation demonstrates n-Step TD methods applied to a random walk environment. The agent learns to predict the value function for states by updating based on returns calculated over $n$-step transitions. This code implements an $n$-step TD algorithm to solve a random walk problem in a finite environment. The agent starts at the middle of the environment and learns a value function for each state based on episodic interactions, where it moves left or right randomly until reaching one of the terminal states. The algorithm allows experimentation with varying $n$ values, which control how far into the future rewards are considered when updating the value function. The goal is to analyze how different $n$-step updates influence the learning process.
use std::collections::HashMap;
use rand::Rng;
// Define a random walk environment
struct RandomWalk {
size: usize,
terminal_states: (usize, usize),
}
impl RandomWalk {
fn step(&self, state: usize, action: i32) -> (usize, f64) {
let next_state = if action == -1 {
state.saturating_sub(1) // Move left
} else {
(state + 1).min(self.size - 1) // Move right
};
let reward = if next_state == self.terminal_states.0 || next_state == self.terminal_states.1 {
1.0 // Reward at terminal states
} else {
0.0
};
(next_state, reward)
}
}
// n-Step TD algorithm
fn n_step_td(
random_walk: &RandomWalk,
episodes: usize,
alpha: f64,
gamma: f64,
n: usize,
) -> HashMap<usize, f64> {
let mut value_function: HashMap<usize, f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = random_walk.size / 2; // Start at the middle state
let mut states = vec![state];
let mut rewards = Vec::new();
while state != random_walk.terminal_states.0 && state != random_walk.terminal_states.1 {
let action = if rng.gen_bool(0.5) { -1 } else { 1 }; // Random action
let (next_state, reward) = random_walk.step(state, action);
states.push(next_state);
rewards.push(reward);
if states.len() > n {
// Calculate G for n steps
let g: f64 = rewards.iter().take(n).enumerate().fold(0.0, |acc, (i, &r)| {
acc + gamma.powi(i as i32) * r
}) + gamma.powi(n as i32)
* *value_function.get(states.get(n).unwrap_or(&state)).unwrap_or(&0.0);
// Update value function
if !states.is_empty() {
let current_value = value_function.entry(states[0]).or_insert(0.0);
*current_value += alpha * (g - *current_value);
}
// Remove processed state and reward
if !states.is_empty() {
states.remove(0);
}
if !rewards.is_empty() {
rewards.remove(0);
}
}
state = next_state;
}
// Final updates for remaining states
while !states.is_empty() && !rewards.is_empty() {
let g: f64 = rewards.iter().enumerate().fold(0.0, |acc, (i, &r)| {
acc + gamma.powi(i as i32) * r
});
let current_value = value_function.entry(states[0]).or_insert(0.0);
*current_value += alpha * (g - *current_value);
states.remove(0);
rewards.remove(0);
}
}
value_function
}
fn main() {
let random_walk = RandomWalk {
size: 5,
terminal_states: (0, 4),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
for n in [1, 3, 5].iter() {
let value_function = n_step_td(&random_walk, episodes, alpha, gamma, *n);
println!("n: {}, Value Function: {:?}", n, value_function);
}
}
The n_step_td function initializes a value function for all states and simulates episodes where the agent starts in the middle state. At each step, the agent selects an action randomly, transitions to a new state, and receives a reward. The rewards and states are stored, and once enough steps ($n$) are collected, the algorithm computes the return $G$ for the current state by summing discounted rewards and the estimated value of the state $n$ steps ahead. The value function is updated incrementally using the TD error, which is the difference between $G$ and the current estimate. At the end of the episode, any remaining states and rewards are processed to finalize the updates. By adjusting $n$, the algorithm can emphasize short-term or long-term rewards, providing insights into the balance between bias and variance in TD learning.
Compared to the previous code, this experiment investigates the impact of varying nnn values in the nnn-step TD algorithm on the learning process in a random walk environment. While the earlier code executed the TD algorithm without a focus on parameter analysis, this version systematically compares $n = 1, 3, 5$ to observe how shorter vs. longer step updates influence learning dynamics. By visualizing the resulting value functions, the experiment highlights the trade-offs between learning speed, stability, and variance introduced by different $n$ values.
use std::collections::HashMap;
use plotters::prelude::*;
use rand::Rng;
// Define a random walk environment
struct RandomWalk {
size: usize,
terminal_states: (usize, usize),
}
impl RandomWalk {
fn step(&self, state: usize, action: i32) -> (usize, f64) {
let next_state = if action == -1 {
state.saturating_sub(1) // Move left
} else {
(state + 1).min(self.size - 1) // Move right
};
let reward = if next_state == self.terminal_states.0 || next_state == self.terminal_states.1 {
1.0 // Reward at terminal states
} else {
0.0
};
(next_state, reward)
}
}
// n-Step TD algorithm
fn n_step_td(
random_walk: &RandomWalk,
episodes: usize,
alpha: f64,
gamma: f64,
n: usize,
) -> HashMap<usize, f64> {
let mut value_function: HashMap<usize, f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = random_walk.size / 2; // Start at the middle state
let mut states = vec![state];
let mut rewards = Vec::new();
while state != random_walk.terminal_states.0 && state != random_walk.terminal_states.1 {
let action = if rng.gen_bool(0.5) { -1 } else { 1 }; // Random action
let (next_state, reward) = random_walk.step(state, action);
states.push(next_state);
rewards.push(reward);
if states.len() > n {
let g: f64 = rewards.iter().take(n).enumerate().fold(0.0, |acc, (i, &r)| {
acc + gamma.powi(i as i32) * r
}) + gamma.powi(n as i32)
* *value_function.get(states.get(n).unwrap_or(&state)).unwrap_or(&0.0);
let current_value = value_function.entry(states[0]).or_insert(0.0);
*current_value += alpha * (g - *current_value);
states.remove(0);
rewards.remove(0);
}
state = next_state;
}
// Final updates for remaining states
while !states.is_empty() && !rewards.is_empty() {
let g: f64 = rewards.iter().enumerate().fold(0.0, |acc, (i, &r)| {
acc + gamma.powi(i as i32) * r
});
let current_value = value_function.entry(states[0]).or_insert(0.0);
*current_value += alpha * (g - *current_value);
states.remove(0);
rewards.remove(0);
}
}
value_function
}
// Visualization function
fn visualize_n_step_impact(
results: Vec<(usize, HashMap<usize, f64>)>,
output_path: &str,
walk_size: usize,
) {
let root = BitMapBackend::new(output_path, (1024, 768)).into_drawing_area();
root.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root)
.caption("Impact of n on Learning", ("sans-serif", 20))
.margin(10)
.x_label_area_size(30)
.y_label_area_size(30)
.build_cartesian_2d(0..walk_size as i32, 0.0..1.0)
.unwrap();
chart
.configure_mesh()
.x_desc("State")
.y_desc("Value")
.draw()
.unwrap();
for (n, value_function) in results {
let series = (0..walk_size as i32).map(|state| {
let value = *value_function.get(&(state as usize)).unwrap_or(&0.0);
(state, value)
});
chart
.draw_series(LineSeries::new(series, &Palette99::pick(n % 9)))
.unwrap()
.label(format!("n = {}", n))
.legend(move |(x, y)| {
PathElement::new(vec![(x, y), (x + 20, y)], &Palette99::pick(n % 9))
});
}
chart.configure_series_labels().background_style(&WHITE.mix(0.8)).draw().unwrap();
println!("Visualization saved to {}", output_path);
}
fn main() {
let random_walk = RandomWalk {
size: 5,
terminal_states: (0, 4),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
let mut results = Vec::new();
for &n in &[1, 3, 5] {
let value_function = n_step_td(&random_walk, episodes, alpha, gamma, n);
println!("n: {}, Value Function: {:?}", n, value_function);
results.push((n, value_function));
}
visualize_n_step_impact(results, "n_step_impact.png", random_walk.size);
}
The code simulates episodes in a random walk environment, where an agent starts at the middle of a finite state space and moves randomly left or right until reaching a terminal state. The nnn-step TD algorithm collects rewards for nnn steps, computes the return $G$ based on discounted future rewards and value estimates, and updates the value function using the TD error. This process repeats until the agent completes the episode. The experiment runs the algorithm for $n = 1, 3, 5$ across 1,000 episodes, stores the learned value functions, and uses the plotters crate to visualize how each $n$ value impacts the convergence of the value function.
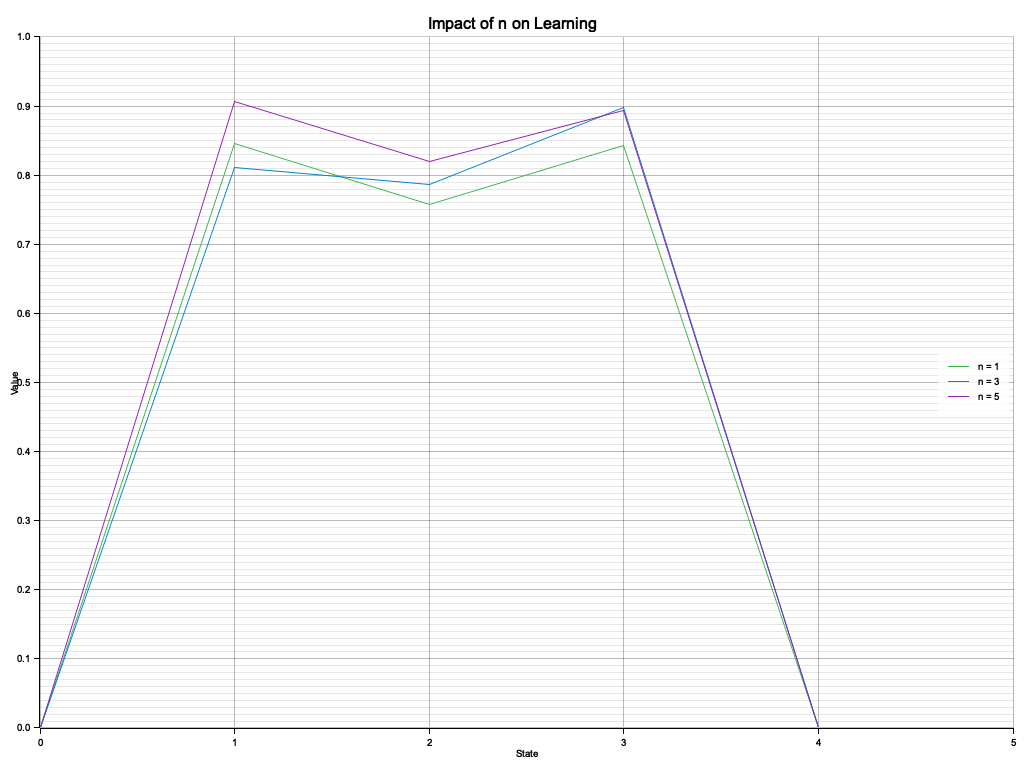
Figure 9: Plotters visualization of n-step experiment.
The results demonstrate clear differences in learning dynamics based on $n$. For smaller $n$ values (e.g., $n = 1$), updates are faster but noisier, reflecting immediate rewards with less emphasis on long-term outcomes. This results in quicker convergence but less stable value functions. Larger $n$ values (e.g., $n = 5$) produce smoother value functions that capture long-term rewards more effectively, but learning is slower and introduces higher variance. The visualization emphasizes the trade-off between responsiveness and stability, showing that the choice of $n$ must align with the desired balance of learning speed and precision in the environment.
This experiment compares three temporal difference (TD) learning approaches—TD(0), Monte Carlo, and nnn-Step TD—in a random walk environment. TD(0) represents the extreme of immediate updates, Monte Carlo waits until the end of an episode to update, and $n$-Step TD acts as a flexible middle ground, balancing between these two extremes. By running the same environment with $n = 1$ (TD(0)), $n = 5$ (Monte Carlo), and $n = 3$ ($n$-Step TD), the experiment highlights how the choice of $n$ affects the trade-offs between computational efficiency, stability, and accuracy in learning.
use std::collections::HashMap;
use rand::Rng;
// Define a random walk environment
struct RandomWalk {
size: usize,
terminal_states: (usize, usize),
}
impl RandomWalk {
fn step(&self, state: usize, action: i32) -> (usize, f64) {
let next_state = if action == -1 {
state.saturating_sub(1) // Move left
} else {
(state + 1).min(self.size - 1) // Move right
};
let reward = if next_state == self.terminal_states.0 || next_state == self.terminal_states.1 {
1.0 // Reward at terminal states
} else {
0.0
};
(next_state, reward)
}
}
// n-Step TD algorithm
fn n_step_td(
random_walk: &RandomWalk,
episodes: usize,
alpha: f64,
gamma: f64,
n: usize,
) -> HashMap<usize, f64> {
let mut value_function: HashMap<usize, f64> = HashMap::new();
let mut rng = rand::thread_rng();
for _ in 0..episodes {
let mut state = random_walk.size / 2; // Start at the middle state
let mut states = vec![state];
let mut rewards = Vec::new();
while state != random_walk.terminal_states.0 && state != random_walk.terminal_states.1 {
let action = if rng.gen_bool(0.5) { -1 } else { 1 }; // Random action
let (next_state, reward) = random_walk.step(state, action);
states.push(next_state);
rewards.push(reward);
if states.len() > n {
let g: f64 = rewards.iter().take(n).enumerate().fold(0.0, |acc, (i, &r)| {
acc + gamma.powi(i as i32) * r
}) + gamma.powi(n as i32)
* *value_function.get(states.get(n).unwrap_or(&state)).unwrap_or(&0.0);
let current_value = value_function.entry(states[0]).or_insert(0.0);
*current_value += alpha * (g - *current_value);
states.remove(0);
rewards.remove(0);
}
state = next_state;
}
// Final updates for remaining states
while !states.is_empty() && !rewards.is_empty() {
let g: f64 = rewards.iter().enumerate().fold(0.0, |acc, (i, &r)| {
acc + gamma.powi(i as i32) * r
});
let current_value = value_function.entry(states[0]).or_insert(0.0);
*current_value += alpha * (g - *current_value);
states.remove(0);
rewards.remove(0);
}
}
value_function
}
fn main() {
let random_walk = RandomWalk {
size: 5,
terminal_states: (0, 4),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
// TD(0) as n = 1
let td_0_values = n_step_td(&random_walk, episodes, alpha, gamma, 1);
println!("TD(0) Value Function: {:?}", td_0_values);
// Monte Carlo as n = size of the random walk
let mc_values = n_step_td(&random_walk, episodes, alpha, gamma, random_walk.size);
println!("Monte Carlo Value Function: {:?}", mc_values);
// n-Step TD as a middle ground
let n_step_values = n_step_td(&random_walk, episodes, alpha, gamma, 3);
println!("n-Step TD (n=3) Value Function: {:?}", n_step_values);
}
The code defines a random walk environment and uses an $n$-Step TD algorithm to estimate state values for each of the three approaches. In TD(0), the algorithm updates state values immediately using one-step returns. For Monte Carlo, it sets nnn equal to the size of the environment, waiting until the episode ends to calculate the full return. The $n$-Step TD implementation for $n = 3$ combines aspects of both, updating state values after considering a limited number of future rewards. By iterating over multiple episodes, the algorithm refines the value function for each state, balancing short-term and long-term reward considerations.
The results demonstrate the distinct characteristics of each approach. TD(0) produces quick updates and computational efficiency but exhibits noisier value functions due to reliance on immediate rewards. Monte Carlo generates smoother and more accurate value estimates by incorporating all future rewards, but it is slower to converge and more computationally intensive. The $n$-Step TD approach with $n = 3$ strikes a balance, capturing longer-term rewards while still updating values more frequently than Monte Carlo. This highlights the flexibility of $n$-Step TD as a practical method that can be tailored to balance efficiency and accuracy depending on the application.
By integrating theory and practical implementations, this section provides a comprehensive understanding of n-Step TD methods, enabling readers to apply them effectively to reinforcement learning tasks using Rust.
6.5. Eligibility Traces and TD(λ)
The concept of eligibility traces arises from the broader challenge in reinforcement learning of credit assignment—determining which past states and actions contributed to an eventual reward. Traditional methods like TD(0) and Monte Carlo represent two ends of the spectrum in this regard. TD(0) focuses on immediate transitions, while Monte Carlo methods consider entire episodes, propagating rewards only after an episode completes. Eligibility traces were introduced as a way to unify these approaches and offer a more flexible mechanism for assigning credit across time.
Richard Sutton, a key figure in reinforcement learning, formalized eligibility traces in the late 1980s as part of his work on Temporal Difference learning. He introduced the idea of maintaining a memory of recently visited states and actions, enabling the algorithm to update their values based on subsequent rewards. This memory decays over time, controlled by a parameter $\lambda$, which determines the balance between short-term and long-term credit assignment.
Figure 10: The evolution and scopes of eligibility traces in RL.
Eligibility traces are central to advanced reinforcement learning methods like TD(λ) and SARSA(λ), where they provide a seamless way to combine the strengths of TD and Monte Carlo approaches. By blending these paradigms, eligibility traces allow algorithms to propagate rewards more effectively in environments with delayed outcomes or sparse rewards, making them particularly useful in complex decision-making tasks.
This topic is fundamental to understanding the intricacies of reinforcement learning and its ability to handle temporal dependencies. Due to its importance, eligibility traces and their applications will be explored in detail in a separate chapter. There, we will delve into the mathematical formulation of eligibility traces, their implementation, and their role in shaping advanced reinforcement learning algorithms.
In reinforcement learning, eligibility traces are a powerful mechanism for assigning credit to states and actions based on how recently they were visited. This allows the learning algorithm to propagate rewards back to not just the immediate predecessor of a state but to all states that contributed to the outcome. Eligibility traces maintain a memory of visited states and decay their influence over time, effectively blending short-term rewards (TD learning) with long-term rewards (Monte Carlo methods).
Eligibility traces are represented as a vector $e(s)$, where each state sss has an associated eligibility value that is updated at each step:
$$ e(s_t) = \gamma \lambda e(s_{t-1}) + 1, $$
where:
$\gamma$ is the discount factor,
$\lambda$ (lambda) is the decay parameter,
$e(s_t)$ is the eligibility trace for state $s_t$.
This mechanism ensures that states visited more recently have higher eligibility, while states visited further in the past have their influence exponentially reduced.
TD(λ) is a generalization of TD(0) and n-Step TD methods, using eligibility traces to unify these approaches into a single framework. The parameter $\lambda$ controls the weight assigned to different returns, creating a spectrum of algorithms:
When$\lambda = 0$, TD(λ) reduces to TD(0), focusing solely on immediate rewards.
When $\lambda = 1$, TD(λ) approximates Monte Carlo methods, incorporating full episodic returns.
For $0 < \lambda < 1$, TD(λ) blends short-term and long-term returns, providing a flexible balance between bias and variance.
The value function in TD(λ) is updated using the TD error and the eligibility traces:
$$ V(s) \leftarrow V(s) + \alpha \delta_t e(s), $$
where:
$\delta_t = R_{t+1} + \gamma V(s_{t+1}) - V(s_t)$ is the TD error,
$e(s)$ is the eligibility trace for state sss.
An intuitive analogy for TD(λ) is learning to play an instrument. Immediate feedback helps you refine your most recent actions (e.g., a wrong note), while occasional reviews of your overall performance improve long-term skills.
The parameter $\lambda$ plays a crucial role in balancing bootstrapping and full returns:
Smaller values of $\lambda$ prioritize immediate updates, making the algorithm faster but potentially less stable in high-variance environments.
Larger values of $\lambda$ incorporate more historical information, improving stability but at the cost of slower updates.
Mathematically, the total return in TD(λ) is a weighted combination of n-step returns:
$$ G_t^\lambda = (1 - \lambda) \sum_{n=1}^\infty \lambda^{n-1} G_t^{(n)}, $$
where $G_t^{(n)}$ is the n-step return. This equation illustrates how TD(λ) seamlessly integrates information from multiple steps.
The following code implements the TD(λ) algorithm with eligibility traces in a grid world environment. The agent learns to estimate the value function for each state through repeated interactions, where it navigates from a starting position to a goal state while maximizing rewards. The TD(λ) algorithm combines elements of both Monte Carlo and temporal difference methods, using eligibility traces to credit multiple states visited during an episode, with the decay rate controlled by the parameter λ. The experiment evaluates the algorithm for different λ values (0.0, 0.5, and 1.0), showcasing how λ affects the learning process.
use std::collections::HashMap;
use rand::Rng;
// Define a grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 }; // Reward for goal
(next_state, reward)
}
}
// TD(λ) with eligibility traces
fn td_lambda(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for episode in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
println!("Episode {} - Start State: {:?}", episode + 1, state);
while state != grid_world.goal_state {
let action = rng.gen_range(0..4); // Random action
let (next_state, reward) = grid_world.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
println!("State: {:?}, Action: {}, Next State: {:?}, Reward: {}, TD Error: {:.4}",
state, action, next_state, reward, td_error);
eligibility_traces
.entry(state)
.and_modify(|e| *e = gamma * lambda * *e + 1.0)
.or_insert(1.0);
println!("Updated Eligibility Traces: {:?}", eligibility_traces);
for (s, e) in &eligibility_traces {
value_function
.entry(*s)
.and_modify(|v| *v += alpha * td_error * e)
.or_insert(alpha * td_error * e);
}
eligibility_traces.retain(|_, e| *e > 1e-6); // Remove negligible traces
state = next_state;
println!("Updated Value Function: {:?}", value_function);
}
println!("End of Episode {}\n", episode + 1);
}
value_function
}
fn main() {
let grid_world = GridWorld {
size: 5,
goal_state: (4, 4),
};
let episodes = 10; // Reduced episodes for more detailed output
let alpha = 0.1;
let gamma = 0.9;
for lambda in [0.0, 0.5, 1.0].iter() {
println!("Running TD(λ) with λ = {:.1}", lambda);
let value_function = td_lambda(&grid_world, episodes, alpha, gamma, *lambda);
println!("λ: {:.1}, Final Value Function: {:?}\n", lambda, value_function);
}
}
The td_lambda function initializes a value function and eligibility traces, which are updated during each episode based on the TD error calculated for the current state and reward. The TD error reflects the difference between the observed reward (plus the discounted future value) and the current estimate. Eligibility traces assign credit to states proportionally to their visitation recency, decaying over time based on λ and γ (discount factor). For each λ value, the algorithm simulates episodes where the agent takes random actions until reaching the goal, updating the value function incrementally. By running the algorithm for multiple λ values, the code highlights the trade-offs between focusing on immediate feedback (λ = 0.0) and crediting long-term rewards (λ = 1.0).
This experiment explores how varying $\lambda$ in the TD($\lambda$) algorithm influences the learning process in a grid world environment. The parameter $\lambda$ controls the balance between immediate and long-term rewards, with $\lambda = 0.0$ prioritizing immediate updates, $\lambda = 1.0$ focusing entirely on long-term rewards, and intermediate values balancing the two. The experiment evaluates the algorithm for $\lambda = 0.0, 0.5, 1.0$, running 1,000 episodes for each case and visualizing the resulting value functions to analyze the trade-offs between learning speed, stability, and accuracy.
use std::collections::HashMap;
use plotters::prelude::*;
use rand::Rng;
// Define a grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 }; // Reward for reaching the goal
(next_state, reward)
}
}
// TD(λ) with eligibility traces
fn td_lambda(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for episode in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
// Log episode start
if episode % 10 == 0 {
println!("Episode {}: Start", episode + 1);
}
while state != grid_world.goal_state {
let action = rng.gen_range(0..4); // Random action
let (next_state, reward) = grid_world.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
eligibility_traces
.entry(state)
.and_modify(|e| *e = gamma * lambda * *e + 1.0)
.or_insert(1.0);
for (s, e) in &eligibility_traces {
value_function
.entry(*s)
.and_modify(|v| *v += alpha * td_error * e)
.or_insert(alpha * td_error * e);
}
eligibility_traces.retain(|_, e| *e > 1e-6); // Remove negligible traces
state = next_state;
}
// Log episode end
if episode % 10 == 0 {
println!("Episode {}: End", episode + 1);
}
}
value_function
}
// Visualization function
fn visualize_lambda_impact(
results: Vec<(f64, HashMap<(usize, usize), f64>)>,
grid_size: usize,
output_path: &str,
) {
let root = BitMapBackend::new(output_path, (1024, 768)).into_drawing_area();
root.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root)
.caption("Impact of λ on Learning", ("sans-serif", 20))
.margin(10)
.x_label_area_size(30)
.y_label_area_size(30)
.build_cartesian_2d(0..grid_size as i32, -10.0..10.0)
.unwrap();
chart
.configure_mesh()
.x_desc("State (flattened)")
.y_desc("Value Estimate")
.draw()
.unwrap();
for (lambda, value_function) in results {
let series = (0..grid_size as i32 * grid_size as i32).map(|index| {
let state = ((index / grid_size as i32) as usize, (index % grid_size as i32) as usize);
let value = *value_function.get(&state).unwrap_or(&0.0);
(index, value)
});
chart
.draw_series(LineSeries::new(series, &Palette99::pick((lambda * 10.0) as usize % 9)))
.unwrap()
.label(format!("λ = {:.1}", lambda))
.legend(move |(x, y)| {
PathElement::new(vec![(x, y), (x + 20, y)], &Palette99::pick((lambda * 10.0) as usize % 9))
});
}
chart.configure_series_labels().background_style(&WHITE.mix(0.8)).draw().unwrap();
println!("Visualization saved to {}", output_path);
}
fn main() {
let grid_world = GridWorld {
size: 5,
goal_state: (4, 4),
};
let episodes = 10; // Reduced for detailed output
let alpha = 0.1;
let gamma = 0.9;
let mut results = Vec::new();
for &lambda in &[0.0, 0.5, 1.0] {
println!("Running TD(λ) with λ = {:.1}", lambda);
let value_function = td_lambda(&grid_world, episodes, alpha, gamma, lambda);
println!("λ: {:.1}, Final Value Function: {:?}\n", lambda, value_function);
results.push((lambda, value_function));
}
visualize_lambda_impact(results, grid_world.size, "lambda_impact.png");
}
The code implements the TD($\lambda$) algorithm with eligibility traces, where each state accumulates credit based on its recency of visitation and the decay factor $\lambda$. The algorithm calculates the TD error for each step, propagates it through eligibility traces, and updates the value function accordingly. The td_lambda function is executed for three $\lambda$ values, and the resulting value functions are stored. These functions are visualized using the plotters crate, with the x-axis representing flattened states and the y-axis showing the value estimates, providing a comparative view of how $\lambda$ affects learning.
The experiment demonstrates the trade-offs inherent in $\lambda$. For $\lambda = 0.0$, the updates are fast and responsive, focusing only on immediate rewards, but this leads to noisier and less stable value estimates. At $\lambda = 1.0$, the algorithm prioritizes long-term rewards, resulting in smoother and more accurate value functions but at the cost of slower updates and convergence. The intermediate $\lambda = 0.5$ strikes a balance, achieving reasonable accuracy while retaining faster updates. These results highlight $\lambda$'s flexibility in tailoring TD ($\lambda$) to specific reinforcement learning scenarios, balancing computational efficiency and stability.
This experiment compares three reinforcement learning methods—TD(0), TD(λ=0.5), and Monte Carlo (approximated by TD(λ=1.0))—in the same grid world environment. The goal is to explore how these approaches differ in balancing short-term and long-term reward estimation. TD(0) focuses on immediate rewards with fast updates, while Monte Carlo relies on the complete trajectory, emphasizing long-term accuracy. TD(λ) bridges the gap, combining both immediate and future rewards based on the parameter λ. The experiment visualizes the value functions of these methods to highlight their trade-offs in learning speed, stability, and accuracy.
use std::collections::HashMap;
use plotters::prelude::*;
use rand::Rng;
// Define a grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 }; // Reward for reaching the goal
(next_state, reward)
}
}
// TD(λ) with eligibility traces
fn td_lambda(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut rng = rand::thread_rng();
for episode in 0..episodes {
let mut state = (0, 0); // Start at the top-left corner
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
if episode % 100 == 0 {
println!("Starting Episode {}", episode + 1);
}
while state != grid_world.goal_state {
let action = rng.gen_range(0..4); // Random action
let (next_state, reward) = grid_world.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
eligibility_traces
.entry(state)
.and_modify(|e| *e = gamma * lambda * *e + 1.0)
.or_insert(1.0);
for (s, e) in &eligibility_traces {
value_function
.entry(*s)
.and_modify(|v| *v += alpha * td_error * e)
.or_insert(alpha * td_error * e);
}
eligibility_traces.retain(|_, e| *e > 1e-6); // Remove negligible traces
if episode % 100 == 0 {
println!(
"Episode {}: State {:?} -> {:?}, Action {}, Reward {}, TD Error {:.4}",
episode + 1,
state,
next_state,
action,
reward,
td_error
);
}
state = next_state;
}
if episode % 100 == 0 {
println!("Ending Episode {}. Current Value Function: {:?}", episode + 1, value_function);
}
}
value_function
}
// Visualization function
fn visualize_td_comparison(
results: Vec<(String, HashMap<(usize, usize), f64>)>,
grid_size: usize,
output_path: &str,
) {
let root = BitMapBackend::new(output_path, (1024, 768)).into_drawing_area();
root.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root)
.caption("Comparison of TD(0), TD(λ), and Monte Carlo", ("sans-serif", 20))
.margin(10)
.x_label_area_size(30)
.y_label_area_size(30)
.build_cartesian_2d(0..grid_size as i32, -10.0..10.0)
.unwrap();
chart
.configure_mesh()
.x_desc("State (flattened)")
.y_desc("Value Estimate")
.draw()
.unwrap();
for (label, value_function) in results {
let label_clone = label.clone(); // Clone the label for reuse
let series = (0..grid_size as i32 * grid_size as i32).map(|index| {
let state = ((index / grid_size as i32) as usize, (index % grid_size as i32) as usize);
let value = *value_function.get(&state).unwrap_or(&0.0);
(index, value)
});
chart
.draw_series(LineSeries::new(series, &Palette99::pick(label.len() % 9)))
.unwrap()
.label(label_clone) // Use the cloned label here
.legend(move |(x, y)| {
PathElement::new(vec![(x, y), (x + 20, y)], &Palette99::pick(label.len() % 9))
});
}
chart.configure_series_labels().background_style(&WHITE.mix(0.8)).draw().unwrap();
println!("Visualization saved to {}", output_path);
}
fn main() {
let grid_world = GridWorld {
size: 5,
goal_state: (4, 4),
};
let episodes = 1000;
let alpha = 0.1;
let gamma = 0.9;
println!("Running TD(0)...");
let td_0_values = td_lambda(&grid_world, episodes, alpha, gamma, 0.0);
println!("Running TD(λ=0.5)...");
let td_lambda_values = td_lambda(&grid_world, episodes, alpha, gamma, 0.5);
println!("Running Monte Carlo (TD(λ=1.0))...");
let mc_values = td_lambda(&grid_world, episodes, alpha, gamma, 1.0);
// Prepare results for visualization
let results = vec![
("TD(0)".to_string(), td_0_values),
("TD(λ=0.5)".to_string(), td_lambda_values),
("Monte Carlo".to_string(), mc_values),
];
visualize_td_comparison(results, grid_world.size, "td_comparison.png");
}
The code uses the TD(λ) algorithm with eligibility traces to estimate state value functions for the grid world. For each method, the td_lambda function is run with a specific λ value: $0.0$ for TD(0), $0.5$ for intermediate TD(λ), and $1.0$ for Monte Carlo. The eligibility traces assign credit to visited states, decaying over time based on λ. The visualize_td_comparison function plots the value functions for each method, with states represented on the x-axis (flattened indices) and value estimates on the y-axis. The chart highlights how each method learns value estimates for the environment.
The results reveal key differences between the methods. TD(0) provides fast updates and prioritizes immediate rewards, but its value estimates are noisier due to limited consideration of future outcomes. Monte Carlo, on the other hand, focuses on long-term rewards, resulting in smoother and more accurate value functions but requiring more episodes to converge. TD(λ=0.5) offers a balance, combining short-term responsiveness with long-term planning. This flexibility of TD(λ) makes it a versatile tool, allowing reinforcement learning practitioners to tailor their approach to specific application requirements, balancing efficiency and accuracy.
By combining theoretical insights with practical Rust implementations, this section equips readers with a comprehensive understanding of TD(λ) and its role in reinforcement learning. The experiments and comparisons highlight its flexibility, effectiveness, and applicability across diverse tasks.
6.6. Conclusion
Chapter 6 offers an in-depth exploration of Temporal-Difference Learning, equipping readers with the knowledge and skills to implement and optimize these methods using Rust. By mastering TD Learning, readers will gain the ability to solve complex reinforcement learning problems efficiently, bridging the gap between theory and practical application in real-world environments.
6.6.1. Further Learning with GenAI
By engaging with these prompts, you will develop a comprehensive understanding of various TD Learning techniques, such as SARSA, Q-Learning, n-Step TD methods, and TD(λ), and how they can be effectively implemented and optimized using Rust.
Explain the fundamental principles of Temporal-Difference (TD) Learning. How does TD Learning combine elements of both Monte Carlo methods and dynamic programming? Implement TD(0) in Rust and analyze its core components.
Discuss the role of bootstrapping in TD Learning. How does it differentiate TD methods from pure Monte Carlo approaches? Implement a TD(0) algorithm in Rust and explore how bootstrapping impacts the convergence of value estimates.
Explore the significance of the TD error in Temporal-Difference Learning. What does the TD error represent, and how is it used to update value functions? Implement the calculation of TD error in Rust and observe its behavior over multiple episodes.
Analyze the impact of different learning rates on the performance of TD(0) methods. How do learning rates influence the stability and speed of convergence? Experiment with various learning rates in Rust and compare their effects on the TD(0) algorithm.
Examine the role of the discount factor in TD Learning. How does the discount factor affect the balance between immediate and future rewards? Implement TD(0) in Rust with different discount factors and observe their influence on the value function and policy.
Discuss the differences between on-policy and off-policy learning in reinforcement learning. How does SARSA as an on-policy method differ from Q-Learning as an off-policy method? Implement both SARSA and Q-Learning in Rust and compare their performance.
Explore the epsilon-greedy policy in the context of SARSA. How does the epsilon-greedy approach balance exploration and exploitation in on-policy learning? Implement SARSA with an epsilon-greedy policy in Rust and experiment with different epsilon values.
Analyze the convergence properties of SARSA. Under what conditions is SARSA guaranteed to converge to the optimal policy? Implement SARSA in Rust and test its convergence behavior in a simple RL environment.
Discuss the significance of the max operator in Q-Learning. How does Q-Learning's use of the max operator influence its off-policy nature and policy convergence? Implement Q-Learning in Rust and observe the impact of the max operator on the learned policy.
Examine the exploration-exploitation trade-off in Q-Learning. How does the separation of behavior and target policies affect the exploration-exploitation balance? Implement Q-Learning in Rust with various exploration strategies and analyze their effects.
Explore the concept of n-Step TD methods in reinforcement learning. How do n-Step TD methods extend TD(0) by incorporating multiple steps before making an update? Implement an n-Step TD method in Rust and compare it with TD(0) in terms of bias and variance.
Analyze the trade-offs between short-term and long-term returns in n-Step TD methods. How does the choice of n influence the balance between accuracy and computational cost? Experiment with different n values in Rust and observe their effects on the learning process.
Discuss the relationship between n-Step TD methods and eligibility traces. How do eligibility traces generalize the concept of n-Step TD methods in reinforcement learning? Implement eligibility traces in Rust and explore their impact on the convergence of value functions.
Examine the concept of TD(λ) in reinforcement learning. How does TD(λ) combine the strengths of both TD(0) and n-Step TD methods using eligibility traces? Implement TD(λ) in Rust and experiment with different λ values to understand their impact on the learning process.
Explore the role of eligibility traces in propagating rewards in TD(λ). How do eligibility traces assign credit to states based on their recency? Implement eligibility traces in Rust and analyze how they influence the convergence of the TD(λ) algorithm.
Discuss the impact of λ (lambda) on the performance of TD(λ) methods. How does varying λ affect the balance between immediate and delayed rewards? Experiment with different λ values in Rust and compare their effects on the stability and accuracy of the value function.
Analyze the differences between TD(0), SARSA, Q-Learning, and TD(λ). How do these TD methods compare in terms of bias, variance, convergence speed, and computational cost? Implement these methods in Rust and conduct a comparative study on their performance in various RL tasks.
Explore the challenges of applying TD Learning to continuous state spaces. What modifications are necessary to adapt TD methods to continuous environments? Implement a TD Learning algorithm in Rust for a continuous state space and analyze the challenges encountered.
Discuss the importance of Rust’s performance capabilities in implementing TD Learning algorithms for large-scale RL problems. How can Rust’s features be leveraged to optimize the performance of TD Learning simulations? Implement a large-scale TD Learning simulation in Rust and evaluate its performance.
Examine the ethical considerations of applying TD Learning methods in real-world scenarios, such as autonomous systems or financial trading. What risks are associated with these applications, and how can they be mitigated? Implement a TD Learning method in Rust for a real-world-inspired scenario and discuss the ethical implications of its deployment.
Let these prompts inspire you to experiment, innovate, and push the boundaries of your knowledge, ultimately mastering the tools needed to apply TD Learning to complex real-world challenges in reinforcement learning.
6.6.2. Hands On Practices
These exercises encourage hands-on experimentation and deep engagement with the concepts, enabling readers to apply their knowledge practically.
Exercise 6.1: Implementing TD(0) and Analyzing Convergence Behavior
Task:
Implement the TD(0) algorithm in Rust to estimate the value function for a simple episodic task, such as navigating a grid world.
Challenge:
Experiment with different learning rates and discount factors to observe their effects on the convergence of the value function. Analyze how the choice of these parameters influences the stability and speed of the algorithm’s convergence.
Visualize the TD error over time and interpret its significance in the learning process.
Exercise 6.2: Implementing and Comparing SARSA and Q-Learning
Task:
Implement both SARSA (on-policy) and Q-Learning (off-policy) algorithms in Rust for a reinforcement learning task, such as balancing a cart-pole or navigating a maze.
Challenge:
Compare the performance of SARSA and Q-Learning in terms of convergence speed, stability, and policy quality. Experiment with different epsilon values in the epsilon-greedy policy to explore how exploration influences the learning process in each algorithm.
Analyze the impact of the on-policy vs. off-policy distinction on the learned policies.
Exercise 6.3: Implementing n-Step TD Methods
Task:
Implement an n-Step TD method in Rust for a reinforcement learning task, such as a random walk or a control problem.
Challenge:
Experiment with different values of n to observe how the algorithm balances bias and variance. Analyze the trade-offs between short-term and long-term returns as n increases.
Compare the performance of the n-Step TD method with TD(0) and Monte Carlo methods in terms of convergence speed, accuracy, and computational cost.
Exercise 6.4: Implementing and Tuning TD(λ) with Eligibility Traces
Task:
Implement the TD(λ) algorithm in Rust, using eligibility traces to combine information from multiple steps before making updates to the value function.
Challenge:
Experiment with different values of λ (lambda) to understand how it influences the balance between bootstrapping and full returns. Analyze how eligibility traces propagate rewards and assign credit to states based on their recency.
Compare the performance of TD(λ) with TD(0) and n-Step TD methods in various reinforcement learning tasks, focusing on flexibility and effectiveness.
Exercise 6.5: Applying TD Learning to Continuous State Spaces
Task:
Implement a TD Learning algorithm in Rust for a reinforcement learning task with a continuous state space, such as controlling a robotic arm or navigating a continuous grid world.
Challenge:
Explore the challenges of applying TD methods to continuous environments, including issues with state representation and value function approximation. Experiment with different techniques to discretize the state space or apply function approximation methods.
Analyze the performance of your TD Learning implementation in the continuous state space, comparing it to a similar task in a discrete state space, focusing on convergence and accuracy.
By implementing these techniques in Rust and experimenting with different scenarios and strategies, you will deepen your understanding of the fundamental concepts and learn how to optimize TD Learning algorithms for real-world applications.
Comments