7.1. Introduction to Function Approximation link

The evolution of function approximation in reinforcement learning (RL) stems from the need to address the limitations of early RL methods when dealing with large or continuous state spaces. Initially, algorithms like Temporal-Difference (TD) learning and Q-Learning relied on tabular representations, maintaining explicit values for every possible state or state-action pair. While effective for small, discrete environments, these tabular methods quickly became impractical as the complexity of tasks increased, suffering from the "curse of dimensionality."

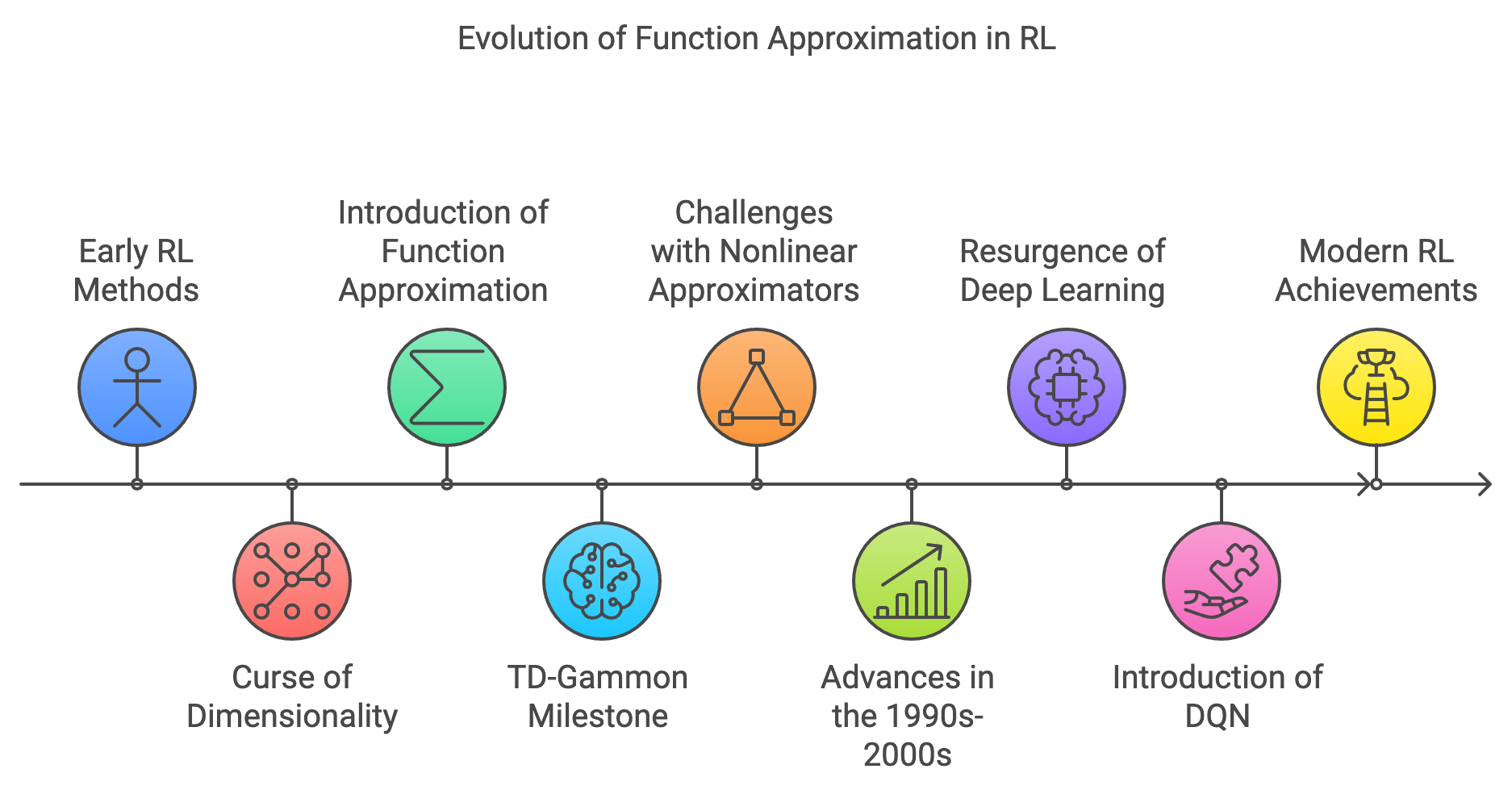
Figure 1: Historical evolution journey of Function Approximation in RL.

In the late 1980s and early 1990s, researchers began exploring ways to generalize learning across similar states to make RL scalable to real-world problems. Function approximation methods were introduced as a solution, aiming to represent value functions using parameterized functions rather than explicit tables. Early approaches utilized linear function approximators, where the value of a state was estimated as a weighted sum of features derived from that state. This allowed for generalization but was limited in capturing complex patterns in the data.

A significant milestone in the journey of function approximation was Gerald Tesauro's work in 1992 with TD-Gammon, a backgammon-playing program. TD-Gammon employed a multilayer neural network to approximate the value function, learning directly from self-play without explicit programming of backgammon strategies. The success of TD-Gammon demonstrated the potential of combining RL with nonlinear function approximators, specifically neural networks, to handle complex tasks.

However, integrating reinforcement learning with nonlinear function approximation introduced new challenges. Early attempts often faced stability and convergence issues, as the theoretical understanding of RL algorithms with function approximators was still developing. The divergence of value estimates and oscillations in learning highlighted the need for more robust methods and a deeper theoretical foundation.

Throughout the 1990s and early 2000s, researchers worked on establishing convergence guarantees and improving the stability of RL algorithms with function approximation. Techniques such as gradient descent methods, residual algorithms, and the development of more sophisticated function approximators contributed to progress in the field.

The resurgence of interest in deep learning in the 2010s provided new tools and perspectives. The advent of deep neural networks offered powerful function approximators capable of processing high-dimensional inputs, such as images and raw sensor data. In 2013, DeepMind introduced the Deep Q-Network (DQN), which successfully combined Q-Learning with deep neural networks to play Atari 2600 games at a human-level performance. DQN addressed previous stability issues by introducing experience replay and target networks, marking a significant breakthrough in deep reinforcement learning.

Since then, the integration of deep learning and reinforcement learning has accelerated, leading to remarkable achievements in areas like game playing, robotics, and autonomous systems. Function approximation has become an essential component of modern RL algorithms, enabling agents to operate in complex, high-dimensional environments where tabular methods are infeasible.

In reinforcement learning, function approximation addresses the challenges of dealing with large or continuous state spaces where tabular methods, like those used in basic TD learning or Q-Learning, become impractical. Instead of maintaining explicit values for each state or state-action pair, function approximators generalize across states by learning a mapping from the state (or state-action pair) to its corresponding value. This enables efficient learning and decision-making even in high-dimensional environments.

Mathematically, function approximation replaces the exact value function $V(s)$ or $Q(s, a)$ with a parameterized function $\hat{V}(s; \mathbf{w})$ or $\hat{Q}(s, a; \mathbf{w})$, where $\mathbf{w}$ represents the parameters of the approximator. For example:

$$ \hat{V}(s; \mathbf{w}) = \sum_{i=1}^d w_i \phi_i(s), $$

where:

• $\phi_i(s)$ are feature functions that extract relevant information from the state,

• $\mathbf{w} = [w_1, w_2, \ldots, w_d]$ are the weights learned during training,

• $d$ is the number of features.

The choice of $\phi_i(s)$ and the structure of the approximator (e.g., linear vs. non-linear) significantly impact the performance and efficiency of reinforcement learning algorithms.

Linear Function Approximation: In linear function approximation, the approximator combines features linearly:

$$ \hat{V}(s; \mathbf{w}) = \mathbf{w}^\top \mathbf{\phi}(s). $$

This method is computationally efficient and interpretable but may struggle to capture complex relationships in the state space.

Non-Linear Function Approximation: Non-linear methods, such as neural networks, use more complex mappings to approximate value functions:

$$ \hat{V}(s; \mathbf{w}) = f(s; \mathbf{w}), $$

where $f$ is a non-linear function like a multi-layer neural network. While powerful, non-linear approximators are computationally intensive and require careful tuning to avoid overfitting.

Function approximation introduces a trade-off between generalization and approximation error:

• Generalization: The ability to apply learned knowledge to unseen states by exploiting the structure of the state space.

• Approximation Error: The difference between the true value and the predicted value due to the limitations of the approximator.

An effective function approximator minimizes approximation error while maintaining the capacity to generalize across states. Balancing this trade-off is essential for successful learning in large or continuous environments.

The bias-variance trade-off plays a critical role in function approximation. High-bias models, like simple linear approximators, may underfit the data and fail to capture important patterns. In contrast, high-variance models, like overparameterized neural networks, may overfit to the training data, reducing their ability to generalize.

Feature engineering is another crucial aspect of function approximation. Designing effective features $\phi_i(s)$ that capture the essential characteristics of the state space can significantly enhance the approximator's performance. For example, in a grid world, features might include the agent’s distance from the goal or obstacles in the environment.

The random walk scenario models an agent navigating a linear environment with $N$ states, starting from the middle. The agent can take random actions, either moving left or right, until reaching one of two terminal states, where a reward of 1 is received. All other transitions have no reward. This environment is a simplified representation of sequential decision-making tasks, ideal for experimenting with reinforcement learning methods like temporal difference (TD) learning. The goal is to approximate the state value function using linear function approximation.

The code below implements two distinct feature representations for a random walk environment to explore their impact on learning accuracy. The one_hot_features function represents each state as a unique one-hot vector, where only the corresponding state index is set to 1, and the rest are 0. This approach is simple and allows independent learning for each state but lacks the ability to generalize across states. In contrast, the radial_features function uses Radial Basis Functions (RBFs) to create feature vectors. Each RBF encodes the proximity of the current state to all other states, enabling smoother transitions and better generalization by considering relationships between states.

use ndarray::{Array1, Array2};
use rand::Rng;

// Define the random walk environment
struct RandomWalk {
    size: usize,
    terminal_states: (usize, usize),
}

impl RandomWalk {
    fn step(&self, state: usize, action: i32) -> (usize, f64) {
        let next_state = if action == -1 {
            state.saturating_sub(1) // Move left
        } else {
            (state + 1).min(self.size - 1) // Move right
        };

        let reward = if next_state == self.terminal_states.0 || next_state == self.terminal_states.1 {
            1.0 // Reward for reaching terminal states
        } else {
            0.0
        };

        (next_state, reward)
    }

    fn features(&self, state: usize) -> Array1<f64> {
        let mut feature_vector = Array1::zeros(self.size);
        feature_vector[state] = 1.0; // One-hot encoding for the state
        feature_vector
    }
}

// Linear function approximation
fn linear_function_approximation(
    random_walk: &RandomWalk,
    episodes: usize,
    alpha: f64,
    gamma: f64,
) -> Array1<f64> {
    let mut weights = Array1::zeros(random_walk.size); // Initialize weights
    let mut rng = rand::thread_rng();

    for _ in 0..episodes {
        let mut state = random_walk.size / 2; // Start in the middle of the random walk

        while state != random_walk.terminal_states.0 && state != random_walk.terminal_states.1 {
            let action = if rng.gen_bool(0.5) { -1 } else { 1 }; // Random action
            let (next_state, reward) = random_walk.step(state, action);

            let features = random_walk.features(state);
            let next_features = random_walk.features(next_state);

            let current_value = weights.dot(&features);
            let next_value = weights.dot(&next_features);

            // Compute TD error
            let td_error = reward + gamma * next_value - current_value;

            // Update weights
            weights = weights + alpha * td_error * features;

            state = next_state;
        }
    }

    weights
}

fn main() {
    let random_walk = RandomWalk {
        size: 5,
        terminal_states: (0, 4),
    };
    let episodes = 1000;
    let alpha = 0.1;
    let gamma = 0.9;

    let weights = linear_function_approximation(&random_walk, episodes, alpha, gamma);
    println!("Learned Weights: {:?}", weights);
}

The code uses a linear function approximation approach to estimate the value function for the random walk environment. Each state is represented as a one-hot encoded feature vector, and a weight vector is learned to approximate state values as the dot product of weights and features. During each episode, the agent randomly selects an action, computes the TD error (the difference between the observed reward plus the discounted future value and the current estimated value), and updates the weights proportionally to this error. By iterating over multiple episodes, the weights converge to approximate the true value function of the random walk environment. The final learned weights represent the value estimates for each state.

Lets do experiment to evaluate the impact of different feature representations on learning accuracy. The code below uses the function_approximation function to learn state values with both one-hot and RBF feature representations. This function accepts a feature representation function (feature_fn) as a parameter, making it straightforward to compare the performance of one-hot encoding and RBFs. By varying the feature representation, the experiment evaluates how effectively each method generalizes and learns value estimates. The results highlight that RBF features reduce overfitting by sharing weights across similar states, while one-hot encoding assigns independent weights to each state, making it prone to overfitting when data is sparse.

use ndarray::Array1;
use rand::Rng;

// Define the random walk environment
struct RandomWalk {
    size: usize,
    terminal_states: (usize, usize),
}

impl RandomWalk {
    fn step(&self, state: usize, action: i32) -> (usize, f64) {
        let next_state = if action == -1 {
            state.saturating_sub(1) // Move left
        } else {
            (state + 1).min(self.size - 1) // Move right
        };

        let reward = if next_state == self.terminal_states.0 || next_state == self.terminal_states.1 {
            1.0 // Reward for reaching terminal states
        } else {
            0.0
        };

        (next_state, reward)
    }

    // One-hot encoding features
    fn one_hot_features(&self, state: usize) -> Array1<f64> {
        let mut feature_vector = Array1::zeros(self.size);
        feature_vector[state] = 1.0; // One-hot encoding for the state
        feature_vector
    }

    // Radial basis function (RBF) features
    fn radial_features(&self, state: usize) -> Array1<f64> {
        let mut feature_vector = Array1::zeros(self.size);
        for i in 0..self.size {
            feature_vector[i] = (-((state as f64 - i as f64).powi(2)) / 2.0).exp(); // Radial basis function
        }
        feature_vector
    }
}

// Function approximation
fn function_approximation(
    random_walk: &RandomWalk,
    episodes: usize,
    alpha: f64,
    gamma: f64,
    feature_fn: fn(&RandomWalk, usize) -> Array1<f64>,
) -> Array1<f64> {
    let mut weights = Array1::zeros(random_walk.size); // Initialize weights
    let mut rng = rand::thread_rng();

    for _ in 0..episodes {
        let mut state = random_walk.size / 2; // Start in the middle of the random walk

        while state != random_walk.terminal_states.0 && state != random_walk.terminal_states.1 {
            let action = if rng.gen_bool(0.5) { -1 } else { 1 }; // Random action
            let (next_state, reward) = random_walk.step(state, action);

            let features = feature_fn(random_walk, state);
            let next_features = feature_fn(random_walk, next_state);

            let current_value = weights.dot(&features);
            let next_value = weights.dot(&next_features);

            // Compute TD error
            let td_error = reward + gamma * next_value - current_value;

            // Update weights
            weights = weights + alpha * td_error * features;

            state = next_state;
        }
    }

    weights
}

fn main() {
    let random_walk = RandomWalk {
        size: 5,
        terminal_states: (0, 4),
    };
    let episodes = 1000;
    let alpha = 0.1;
    let gamma = 0.9;

    // Using one-hot encoding
    println!("Using One-Hot Encoding Features:");
    let one_hot_weights = function_approximation(&random_walk, episodes, alpha, gamma, RandomWalk::one_hot_features);
    println!("Learned Weights (One-Hot): {:?}", one_hot_weights);

    // Using radial basis function (RBF) features
    println!("Using Radial Basis Function Features:");
    let rbf_weights = function_approximation(&random_walk, episodes, alpha, gamma, RandomWalk::radial_features);
    println!("Learned Weights (RBF): {:?}", rbf_weights);
}

The experiment begins by initializing a random walk environment with 5 states and terminal rewards at the boundaries. For each state, both one-hot encoding and RBF features are used as input to a linear function approximator. The approximator is trained using Temporal Difference (TD) learning, which iteratively updates weights based on the TD error—calculated as the difference between predicted and observed rewards plus future estimates. After training, the learned weights for each feature representation are printed, allowing direct comparison of the value estimates generated by the two methods.

Using one-hot encoding, each state is treated independently, resulting in sharp transitions between states in the value function. While this approach converges quickly, it may overfit to specific trajectories, limiting its ability to generalize. On the other hand, RBF features provide a smoother interpolation of values between states, as they share weights across similar states. This improves generalization and reduces approximation error, though it may converge more slowly due to the added complexity. Overall, the experiment underscores the importance of feature engineering in reinforcement learning and demonstrates how RBFs can enhance value estimation by leveraging relationships between states.

By combining theoretical foundations with practical Rust implementations, this section equips readers with the tools to apply function approximation effectively in reinforcement learning tasks. The examples illustrate the versatility of linear function approximation and lay the groundwork for exploring more advanced techniques like neural networks.

7.2. Linear Function Approximation link

Linear function approximation emerged as one of the earliest approaches to address the scalability challenges in reinforcement learning, particularly for problems involving large or continuous state spaces. Traditional tabular methods, which store a unique value for each state or state-action pair, become computationally prohibitive when the number of states grows exponentially or when states are represented by continuous variables. To overcome these limitations, researchers turned to the idea of generalization—estimating values for unseen states based on their similarity to observed states.

The foundation of linear function approximation lies in the concept of feature extraction, where states are mapped into a lower-dimensional feature space. Instead of learning explicit values for every state, the value function is represented as a linear combination of these features, weighted by a set of parameters. Formally, the value of a state sss is approximated as:

$$ V(s) \approx \sum_{i=1}^n w_i \phi_i(s), $$

where $\phi_i(s)$ represents the $i$-th feature of the state $s$, and $w_i$ is the corresponding weight. This formulation enables the representation of complex state spaces in a computationally efficient manner while maintaining interpretability.

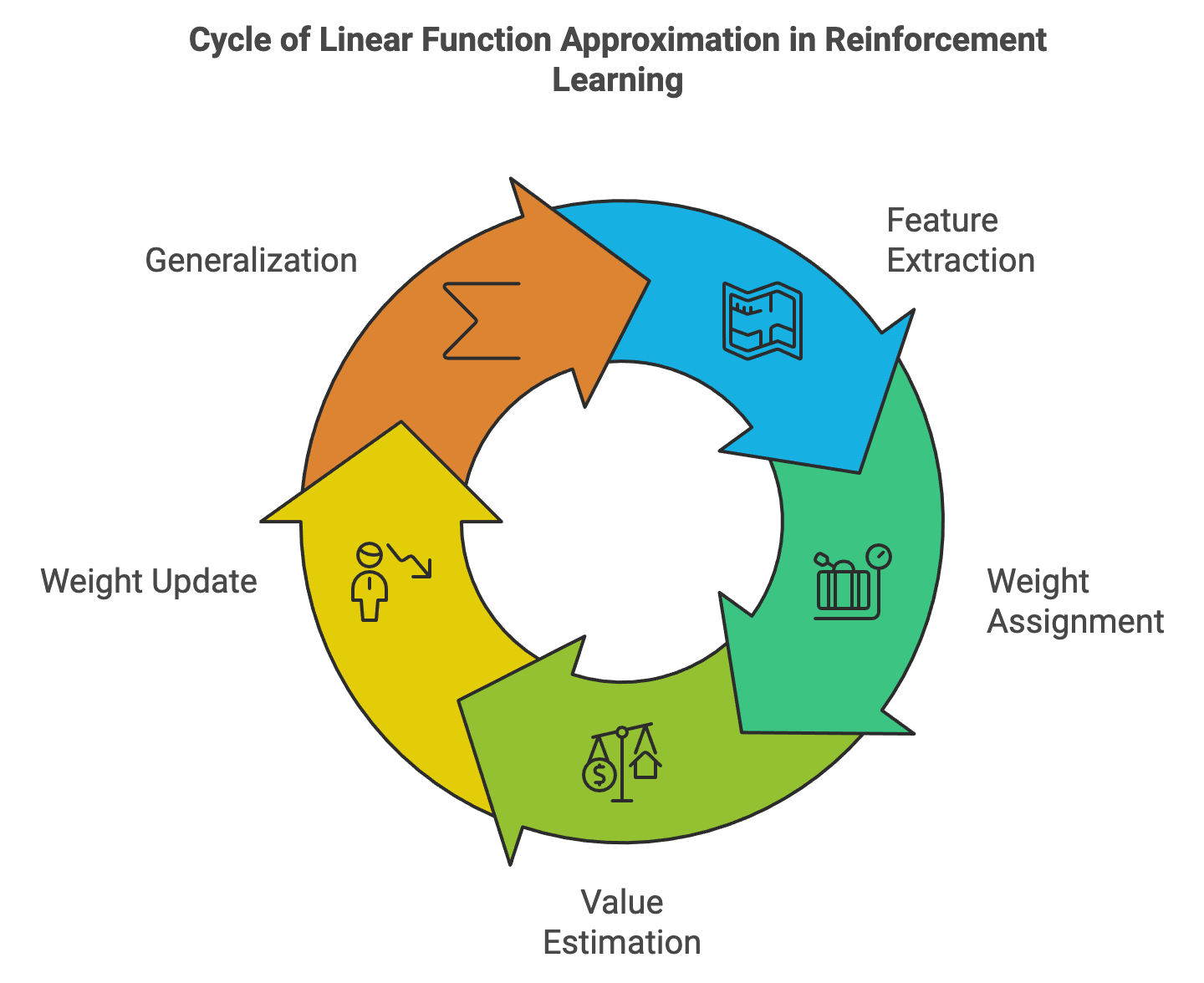
Figure 2: Cycle of linear function approximation.

Linear function approximation gained traction in the late 1980s and early 1990s, particularly with the rise of Temporal-Difference (TD) learning. Its simplicity and efficiency made it a natural choice for combining with TD methods, as the weight updates could be computed incrementally using stochastic gradient descent. Early applications demonstrated its effectiveness in scenarios like resource allocation, navigation tasks, and simple games.

Despite its advantages, linear function approximation comes with inherent limitations. By design, it assumes that the relationship between features and the value function is linear, which may not capture the complexity of certain environments. However, its ease of implementation and theoretical properties, such as convergence guarantees under certain conditions, made it a foundational tool in reinforcement learning.

The success of linear function approximation paved the way for more advanced methods, such as nonlinear approximators using neural networks. While these more complex approaches can model intricate relationships in high-dimensional spaces, linear function approximation remains a valuable baseline, offering insights into the behavior of reinforcement learning algorithms and serving as a stepping stone toward understanding more sophisticated techniques.

Linear function approximation is a foundational technique in reinforcement learning used to estimate value functions or policies by representing them as a weighted sum of features. This method is particularly effective in environments with large or continuous state spaces, where tabular methods become computationally infeasible. By projecting the state space into a feature space and learning a set of weights, linear function approximation provides a scalable way to generalize across states.

Mathematically, the value function $V(s)$ is approximated as:

$$ \hat{V}(s; \mathbf{w}) = \mathbf{w}^\top \mathbf{\phi}(s) = \sum_{i=1}^d w_i \phi_i(s), $$

where:

• $\mathbf{\phi}(s) = [\phi_1(s), \phi_2(s), \ldots, \phi_d(s)]$ is the feature vector representing state $s$,

• $\mathbf{w} = [w_1, w_2, \ldots, w_d]$ are the weights,

• $d$ is the number of features.

Linear function approximation relies on the linearity assumption, which simplifies the learning process but limits its ability to capture non-linear relationships in the data. This makes feature selection critical, as the chosen features must adequately capture the structure of the state space for effective learning.

The linearity assumption states that the value function can be expressed as a linear combination of features. While this assumption simplifies the optimization process, it may introduce bias if the actual value function is highly non-linear. For example, in a grid world, using distance to the goal as a feature may suffice for linear approximation, but complex environments may require more sophisticated features or non-linear methods.

An analogy for understanding this limitation is approximating a curved surface with a flat plane. Linear methods can approximate small regions accurately but struggle with capturing global curvature.

Feature selection plays a crucial role in linear function approximation. Poorly chosen features may lead to underfitting, where the model fails to capture important aspects of the state space. Conversely, using too many irrelevant features can result in overfitting, where the model learns noise rather than underlying patterns.

To mitigate overfitting, regularization techniques such as L2 regularization (Ridge regression) are used. Regularization penalizes large weights, preventing the model from relying too heavily on specific features. The L2 regularized loss function is:

$$ J(\mathbf{w}) = \frac{1}{2} \sum_{s \in S} \left( V(s) - \hat{V}(s; \mathbf{w}) \right)^2 + \frac{\lambda}{2} \|\mathbf{w}\|^2, $$

where $\lambda$ controls the strength of the regularization.

Gradient descent is the most common optimization method for updating weights in linear function approximation. The gradient of the loss function with respect to $\mathbf{w}$ is:

$$ \nabla_{\mathbf{w}} J(\mathbf{w}) = -\sum_{s \in S} \left( V(s) - \hat{V}(s; \mathbf{w}) \right) \mathbf{\phi}(s) + \lambda \mathbf{w}. $$

The weights are updated iteratively using:

$$ \mathbf{w} \leftarrow \mathbf{w} - \alpha \nabla_{\mathbf{w}} J(\mathbf{w}), $$

where $\alpha$ is the learning rate. This process ensures that the weights converge to values that minimize the approximation error, balancing the trade-off between bias and variance.

The code below implements a reinforcement learning experiment in a grid world environment, where an agent learns to approximate the value function using linear function approximation and gradient descent. The grid world consists of $N \times N$ cells, and the agent starts in the top-left corner, navigating randomly until it reaches a designated goal state with a reward of 10.0. The agent employs a one-hot encoding for state features and updates its weights iteratively based on the Temporal Difference (TD) error, gradually learning to predict the long-term value of each state.

use ndarray::Array1;
use rand::Rng;

// Define the grid world environment
struct GridWorld {
    size: usize,
    goal_state: (usize, usize),
}

impl GridWorld {
    fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
        let next_state = match action {
            0 => (state.0.saturating_sub(1), state.1), // Up
            1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
            2 => (state.0, state.1.saturating_sub(1)), // Left
            _ => (state.0, state.1 + 1.min(self.size - 1)), // Right
        };
        let reward = if next_state == self.goal_state { 10.0 } else { -1.0 }; // Reward for goal
        (next_state, reward)
    }

    fn features(&self, state: (usize, usize)) -> Array1<f64> {
        let mut feature_vector = Array1::zeros(self.size * self.size);
        if state.0 < self.size && state.1 < self.size {
            let index = state.0 * self.size + state.1; // Flatten the 2D index
            feature_vector[index] = 1.0; // One-hot encoding
        }
        feature_vector
    }
}

// Linear function approximation with gradient descent
fn linear_function_approximation(
    grid_world: &GridWorld,
    episodes: usize,
    alpha: f64,
    gamma: f64,
    lambda: f64,
) -> Array1<f64> {
    let mut weights = Array1::zeros(grid_world.size * grid_world.size);
    let mut rng = rand::thread_rng();

    for _ in 0..episodes {
        let mut state = (0, 0); // Start at top-left corner

        while state != grid_world.goal_state {
            let action = rng.gen_range(0..4); // Random action
            let (next_state, reward) = grid_world.step(state, action);

            let features = grid_world.features(state);
            let next_features = grid_world.features(next_state);

            let current_value = weights.dot(&features);
            let next_value = weights.dot(&next_features);

            // Compute TD error
            let td_error = reward + gamma * next_value - current_value;

            // Update weights in-place
            for (i, feature_value) in features.iter().enumerate() {
                weights[i] += alpha * (td_error * feature_value - lambda * weights[i]);
            }

            state = next_state;
        }
    }

    weights
}

fn main() {
    let grid_world = GridWorld {
        size: 5,
        goal_state: (4, 4),
    };
    let episodes = 1000;
    let alpha = 0.1;
    let gamma = 0.9;
    let lambda = 0.01;

    let weights = linear_function_approximation(&grid_world, episodes, alpha, gamma, lambda);
    println!("Learned Weights: {:?}", weights);
}

The GridWorld struct defines the environment, including state transitions, rewards, and feature encoding. The agent moves within the grid using random actions, with transitions managed by the step method. State features are represented as one-hot encoded vectors using the features function, mapping each state to a unique vector. The linear_function_approximation function implements the learning process, initializing the weights and updating them iteratively based on the TD error, computed as the difference between predicted and observed rewards plus future value estimates. The learning rate (alpha), discount factor (gamma), and regularization (lambda) control the weight updates. After running multiple episodes, the agent outputs the learned weights, representing the approximated value function for the grid world.

Compared to the original version, this following experiment explores the impact of varying regularization values ($\lambda$) on the weight updates and generalization in a grid world environment. By introducing three different $\lambda$ values (0.0, 0.001, 0.1), the code demonstrates how regularization affects the balance between overfitting and smooth generalization in reinforcement learning. The experiment visualizes learned weights as heatmaps to provide an intuitive understanding of how each $\lambda$ value influences the distribution of learned values across the grid.

use ndarray::Array1;
use plotters::prelude::*;
use rand::Rng;

// Define the grid world environment
struct GridWorld {
    size: usize,
    goal_state: (usize, usize),
}

impl GridWorld {
    fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
        let next_state = match action {
            0 => (state.0.saturating_sub(1), state.1), // Up
            1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
            2 => (state.0, state.1.saturating_sub(1)), // Left
            _ => (state.0, state.1 + 1.min(self.size - 1)), // Right
        };
        let reward = if next_state == self.goal_state { 10.0 } else { -1.0 }; // Reward for goal
        (next_state, reward)
    }

    fn features(&self, state: (usize, usize)) -> Array1<f64> {
        let mut feature_vector = Array1::zeros(self.size * self.size);
        if state.0 < self.size && state.1 < self.size {
            let index = state.0 * self.size + state.1; // Flatten the 2D index
            feature_vector[index] = 1.0; // One-hot encoding
        }
        feature_vector
    }
}

// Linear function approximation with gradient descent
fn linear_function_approximation(
    grid_world: &GridWorld,
    episodes: usize,
    alpha: f64,
    gamma: f64,
    lambda: f64,
) -> Array1<f64> {
    let mut weights = Array1::zeros(grid_world.size * grid_world.size);
    let mut rng = rand::thread_rng();

    for episode in 0..episodes {
        let mut state = (0, 0); // Start at top-left corner
        if episode % 100 == 0 {
            println!("Episode {}: Intermediate weights: {:?}", episode, weights);
        }

        while state != grid_world.goal_state {
            let action = rng.gen_range(0..4); // Random action
            let (next_state, reward) = grid_world.step(state, action);

            let features = grid_world.features(state);
            let next_features = grid_world.features(next_state);

            let current_value = weights.dot(&features);
            let next_value = weights.dot(&next_features);

            // Compute TD error
            let td_error = reward + gamma * next_value - current_value;

            // Update weights in-place
            for (i, feature_value) in features.iter().enumerate() {
                weights[i] += alpha * (td_error * feature_value - lambda * weights[i]);
            }

            state = next_state;
        }
    }

    weights
}

// Visualization function: heatmaps for weights
fn visualize_weights_heatmaps(
    results: Vec<(f64, Array1<f64>)>,
    grid_size: usize,
    output_path: &str,
) {
    let root = BitMapBackend::new(output_path, (1024, 768)).into_drawing_area();
    root.fill(&WHITE).unwrap();

    let areas = root.split_evenly((1, results.len())); // Split into rows for each λ

    for ((lambda, weights), area) in results.into_iter().zip(areas) {
        let reshaped_weights = weights
            .into_shape((grid_size, grid_size))
            .expect("Shape conversion failed");

        let max_weight = reshaped_weights.iter().cloned().fold(f64::NEG_INFINITY, f64::max);
        let min_weight = reshaped_weights.iter().cloned().fold(f64::INFINITY, f64::min);

        let mut chart = ChartBuilder::on(&area)
            .caption(format!("Weights Heatmap (λ = {:.2})", lambda), ("sans-serif", 15))
            .margin(10)
            .x_label_area_size(20)
            .y_label_area_size(20)
            .build_cartesian_2d(0..grid_size, 0..grid_size)
            .unwrap();

        chart.configure_mesh().disable_mesh().draw().unwrap();

        for (x, row) in reshaped_weights.outer_iter().enumerate() {
            for (y, &weight) in row.iter().enumerate() {
                let intensity = if max_weight != min_weight {
                    (weight - min_weight) / (max_weight - min_weight) // Normalize weight
                } else {
                    0.5 // Default intensity for equal weights
                };
                chart
                    .draw_series(std::iter::once(Rectangle::new(
                        [(x, y), (x + 1, y + 1)],
                        ShapeStyle::from(&HSLColor(0.0, 1.0 - intensity, 0.5)).filled(),
                    )))
                    .unwrap();
            }
        }
    }

    println!("Heatmaps saved to {}", output_path);
}

fn main() {
    let grid_world = GridWorld {
        size: 5,
        goal_state: (4, 4),
    };
    let episodes = 1000;
    let alpha = 0.1;
    let gamma = 0.9;

    let mut results = Vec::new();

    for &lambda in &[0.0, 0.01, 0.1] {
        println!("Running linear approximation with λ = {:.2}", lambda);
        let weights = linear_function_approximation(&grid_world, episodes, alpha, gamma, lambda);
        println!("Lambda: {:.2}, Final Weights: {:?}", lambda, weights);
        results.push((lambda, weights));
    }

    visualize_weights_heatmaps(results, grid_world.size, "weights_heatmaps.png");
}

The agent performs a series of random actions in each episode and updates its weight vector based on temporal difference (TD) learning. Regularization is introduced through $\lambda$, which penalizes large weights during updates to encourage generalization. After completing the episodes for each $\lambda$ value, the learned weights are reshaped into a 2D grid and visualized as heatmaps using the plotters crate. Each heatmap shows how weights are distributed across the grid, enabling a direct comparison of the effects of $\lambda$.

The results reveal that low $\lambda$ values (e.g., 0.0) produce sharper transitions in weights, reflecting a tendency to overfit to specific states and actions. Higher $\lambda$ values (e.g., 0.1) lead to smoother weight distributions, indicating better generalization across the grid. The heatmaps also show that higher regularization stabilizes the learning process by reducing noise in the updates, though at the cost of slower convergence. This highlights the trade-off between achieving detailed state-specific value estimates and ensuring a robust, generalized solution in reinforcement learning tasks.

By combining theoretical insights with practical Rust implementations, this section provides a comprehensive understanding of linear function approximation, its applications, and its limitations. The experiments illustrate the importance of feature selection, regularization, and the trade-offs inherent in linear methods.

7.3. Non-Linear Function Approximation with Neural Networks link

While linear function approximation provided a crucial step forward in making reinforcement learning scalable to large or continuous state spaces, its inherent assumption of linearity often proved limiting in capturing the complexities of real-world problems. Many environments exhibit intricate, non-linear relationships between states, actions, and their corresponding values or policies. Addressing this limitation required a more flexible approach to function approximation, one that could model these non-linear relationships effectively.

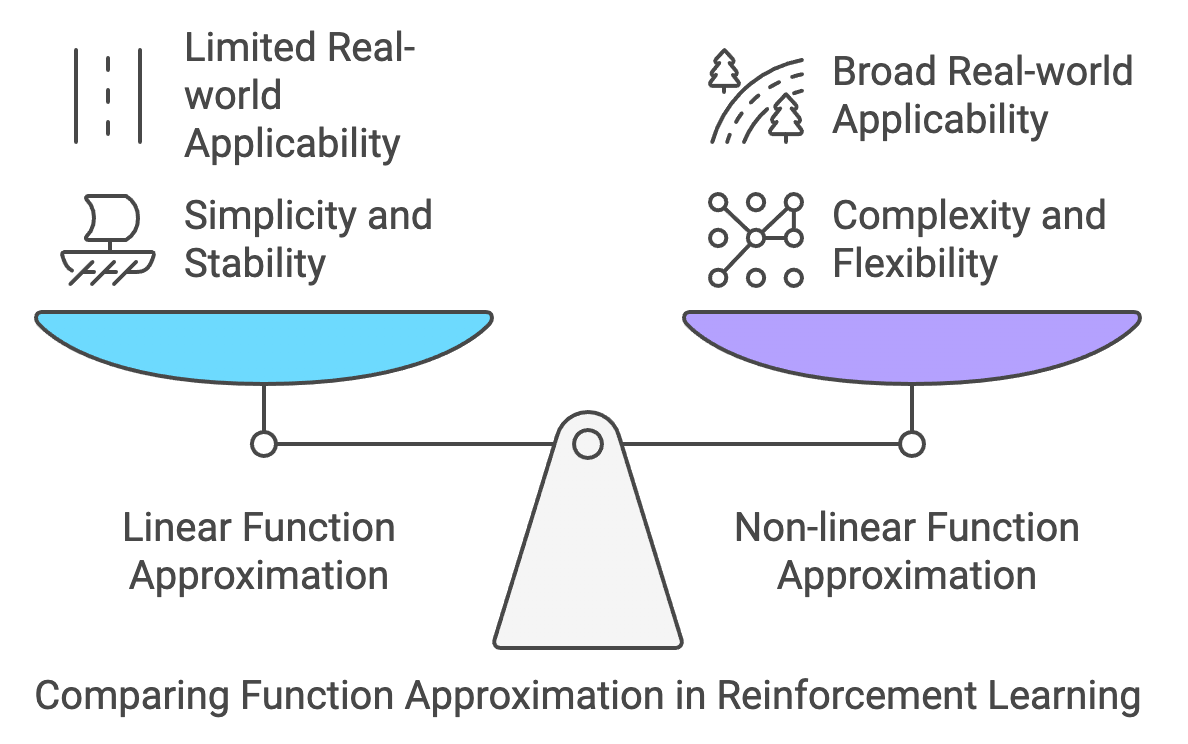
Figure 3: Comparison between linear vs non-linear function approximation in RL.

The exploration of non-linear function approximation in reinforcement learning gained momentum in the late 1980s and early 1990s. Researchers began experimenting with methods that could go beyond the linear constraints of weighted feature combinations. Neural networks emerged as a natural choice, given their success in other areas of machine learning, such as pattern recognition and function approximation. By introducing layers of interconnected nodes with non-linear activation functions, neural networks offered the capacity to learn complex mappings from high-dimensional input spaces to output values.

A pivotal moment in the use of non-linear function approximation came with Gerald Tesauro’s TD-Gammon in 1992. TD-Gammon utilized a multi-layer neural network as a non-linear function approximator to estimate the value function in a backgammon-playing agent. By combining neural networks with Temporal-Difference (TD) learning, the system demonstrated unprecedented performance, achieving a level of play comparable to human experts. This success highlighted the potential of neural networks to handle the non-linear dependencies inherent in many reinforcement learning tasks.

Figure 4: Scopes of non-linear function approximation in RL.

Despite its promise, early applications of non-linear function approximation faced challenges, particularly around stability and convergence. Unlike linear methods, which had well-understood theoretical guarantees, non-linear function approximators could lead to divergence or oscillatory behavior in value estimates. These challenges prompted significant research into techniques for improving stability, including experience replay, target networks, and regularization.

In modern reinforcement learning, non-linear function approximation—primarily through deep neural networks—has become a cornerstone of the field. Advances in optimization techniques, computing power, and algorithm design have made it possible to tackle high-dimensional, non-linear problems across domains like robotics, game playing, and autonomous systems. Neural networks’ ability to approximate intricate mappings between states and values has expanded the scope of what reinforcement learning can achieve, making it an indispensable tool in the RL toolkit.

In reinforcement learning, non-linear function approximation is a powerful method for modeling complex value functions and policies, especially in environments with large or continuous state spaces. Neural networks are the most commonly used non-linear function approximators, offering the flexibility to approximate intricate mappings between states (or state-action pairs) and their corresponding values. Unlike linear function approximation, which relies on weighted sums of features, neural networks use layers of interconnected nodes and non-linear activation functions to capture complex patterns.

Mathematically, a neural network with $L$ layers can be represented as:

$$ \hat{V}(s; \theta) = f_L(f_{L-1}(\cdots f_1(s; \theta_1); \theta_2) \cdots; \theta_L), $$

where:

• $f_l$ represents the transformation at the $l$-th layer, typically a combination of a linear transformation and a non-linear activation function,

• $\theta = \{\theta_1, \theta_2, \ldots, \theta_L\}$ are the parameters (weights and biases) of the network.

This architecture allows neural networks to approximate any continuous function to arbitrary precision, given sufficient depth, width, and training data, a property known as the universal approximation theorem.

A neural network consists of input layers, hidden layers, and output layers:

• Input Layer: Represents the state or state-action pair in the reinforcement learning task. Each node corresponds to a feature.

• Hidden Layers: Perform intermediate computations, transforming inputs into representations that capture essential patterns.

• Output Layer: Produces the approximated value function $\hat{V}(s)$ or policy $\pi(s)$.

Activation functions introduce non-linearity into the network, enabling it to approximate complex functions. Common activation functions include:

• ReLU (Rectified Linear Unit): $f(x) = \max(0, x)$, offering computational efficiency and mitigating the vanishing gradient problem.

• Sigmoid: $f(x) = \frac{1}{1 + e^{-x}}$, useful for probabilistic outputs but prone to vanishing gradients.

• Tanh: $f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$, providing centered outputs but also susceptible to vanishing gradients.

The integration of deep learning into reinforcement learning has revolutionized the field, enabling algorithms like Deep Q-Learning (DQN) and policy gradient methods. Neural networks can approximate high-dimensional value functions, handle continuous action spaces, and learn directly from raw sensory data such as images. The ability to learn complex policies makes deep learning indispensable for solving tasks like robotic control, game playing, and autonomous navigation.

Backpropagation is the algorithm used to train neural networks by minimizing a loss function, such as the mean squared error (MSE) for value function approximation:

$$ L(\theta) = \frac{1}{N} \sum_{i=1}^N \left( \hat{V}(s_i; \theta) - V(s_i) \right)^2, $$

where $N$ is the number of training samples.

The gradient of the loss function with respect to the network parameters θ\\thetaθ is computed using the chain rule, and the weights are updated iteratively using gradient descent:

$$ \theta \leftarrow \theta - \alpha \nabla_\theta L(\theta), $$

where $\alpha$ is the learning rate. This process propagates errors backward through the network, adjusting weights to reduce the discrepancy between predicted and true values.

The following implementation applies a neural network-based function approximator to the cart-pole balancing task. The network approximates the Q-values for state-action pairs, enabling the agent to learn a policy for balancing the pole. The code implements RL framework to train a neural network for the cart-pole problem, a classic control task in RL. The environment (CartPoleEnv) simulates cart-pole dynamics, where the agent balances a pole by taking discrete actions. The neural network (QNetwork) approximates a Q-value function, estimating the expected reward for each state-action pair. The training algorithm uses Temporal Difference (TD) learning with an epsilon-greedy policy for exploration and exploitation.

use tch::{nn, nn::Module, nn::OptimizerConfig, Kind, Tensor};

// Define the cart-pole environment
struct CartPoleEnv {
    state_dim: usize,
    action_dim: usize,
}

impl CartPoleEnv {
    fn step(&self, state: &Tensor, action: usize) -> (Tensor, f64, bool) {
        // Simulate the cart-pole dynamics (simplified)
        let next_state = state + Tensor::from(action as f64 - 0.5);
        let reward = if next_state.abs().max().double_value(&[]) < 1.0 {
            1.0 // Reward for keeping the pole balanced
        } else {
            -1.0 // Penalty for failure
        };
        let done = reward < 0.0;
        (next_state, reward, done)
    }

    fn reset(&self) -> Tensor {
        Tensor::zeros(&[self.state_dim as i64], (Kind::Float, tch::Device::Cpu)).set_requires_grad(false)
    }
}

// Define the neural network architecture
#[derive(Debug)]
struct QNetwork {
    model: nn::Sequential,
}

impl QNetwork {
    fn new(vs: &nn::Path, state_dim: usize, action_dim: usize) -> Self {
        let model = nn::seq()
            .add(nn::linear(vs / "layer1", state_dim as i64, 128, Default::default()))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(vs / "layer2", 128, 128, Default::default()))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(vs / "layer3", 128, action_dim as i64, Default::default()));
        Self { model }
    }

    fn forward(&self, x: &Tensor) -> Tensor {
        self.model.forward(x)
    }
}

// Training the neural network
fn train_cart_pole() {
    let env = CartPoleEnv {
        state_dim: 4,
        action_dim: 2,
    };

    let vs = nn::VarStore::new(tch::Device::Cpu);
    let q_network = QNetwork::new(&vs.root(), env.state_dim, env.action_dim);
    let mut opt = nn::Adam::default().build(&vs, 1e-3).unwrap();

    let episodes = 1000;
    let gamma = 0.99;

    for episode in 0..episodes {
        let mut state = env.reset();
        let mut done = false;

        while !done {
            let q_values = q_network.forward(&state);

            let action = if rand::random::<f64>() < 0.1 {
                rand::random::<usize>() % env.action_dim // Explore
            } else {
                q_values.argmax(-1, false).int64_value(&[]) as usize // Exploit
            };

            let (next_state, reward, terminal) = env.step(&state, action);

            // Compute target and TD error
            let target = reward + gamma * q_network.forward(&next_state.detach()).max().double_value(&[]);
            let td_error = target - q_values.double_value(&[action as i64]);

            println!(
                "Episode: {}, TD Error: {:.4}, Reward: {:.2}",
                episode, td_error, reward
            );

            // Compute and backpropagate loss
            let loss = Tensor::from(td_error).pow(&Tensor::from(2.0)).set_requires_grad(true);
            opt.backward_step(&loss);

            state = next_state.detach(); // Detach to avoid accumulating gradients
            done = terminal;
        }
    }

    println!("Training complete!");
}

fn main() {
    train_cart_pole();
}

The program defines a cart-pole environment where states are updated based on actions, and rewards indicate whether the pole remains balanced. The QNetwork is a feed-forward neural network with two hidden layers, trained to predict Q-values for each action. The training loop iteratively resets the environment, computes actions using an epsilon-greedy policy, and updates the network based on TD error, which measures the difference between the predicted and target Q-values. Gradients are computed using backpropagation, and weights are optimized using the Adam optimizer. The program balances exploration (random actions) and exploitation (selecting the best-known action) to maximize long-term rewards.

By integrating theory with hands-on implementation, this section highlights the transformative power of neural networks in reinforcement learning. Readers gain a deep understanding of non-linear function approximation, its advantages, and the practical challenges of training neural networks in Rust.

7.4. Feature Engineering for Function Approximation link

The development of feature engineering in reinforcement learning is closely tied to the evolution of function approximation methods. As the field progressed from tabular approaches to linear and non-linear function approximators, the importance of extracting meaningful features from raw state representations became increasingly evident. Features serve as the foundation upon which function approximators operate, directly influencing their ability to generalize across states and learn effectively.

In the era of linear function approximation, feature engineering emerged as a critical step in transforming raw state information into a lower-dimensional space where relationships could be modeled as weighted sums. Researchers recognized that poorly chosen features could lead to suboptimal or slow learning, as the approximator might fail to capture essential patterns. Feature selection and transformation techniques, such as polynomial expansion, Fourier basis functions, and tile coding, were developed to improve the representation of state spaces and enhance the performance of linear approximators.

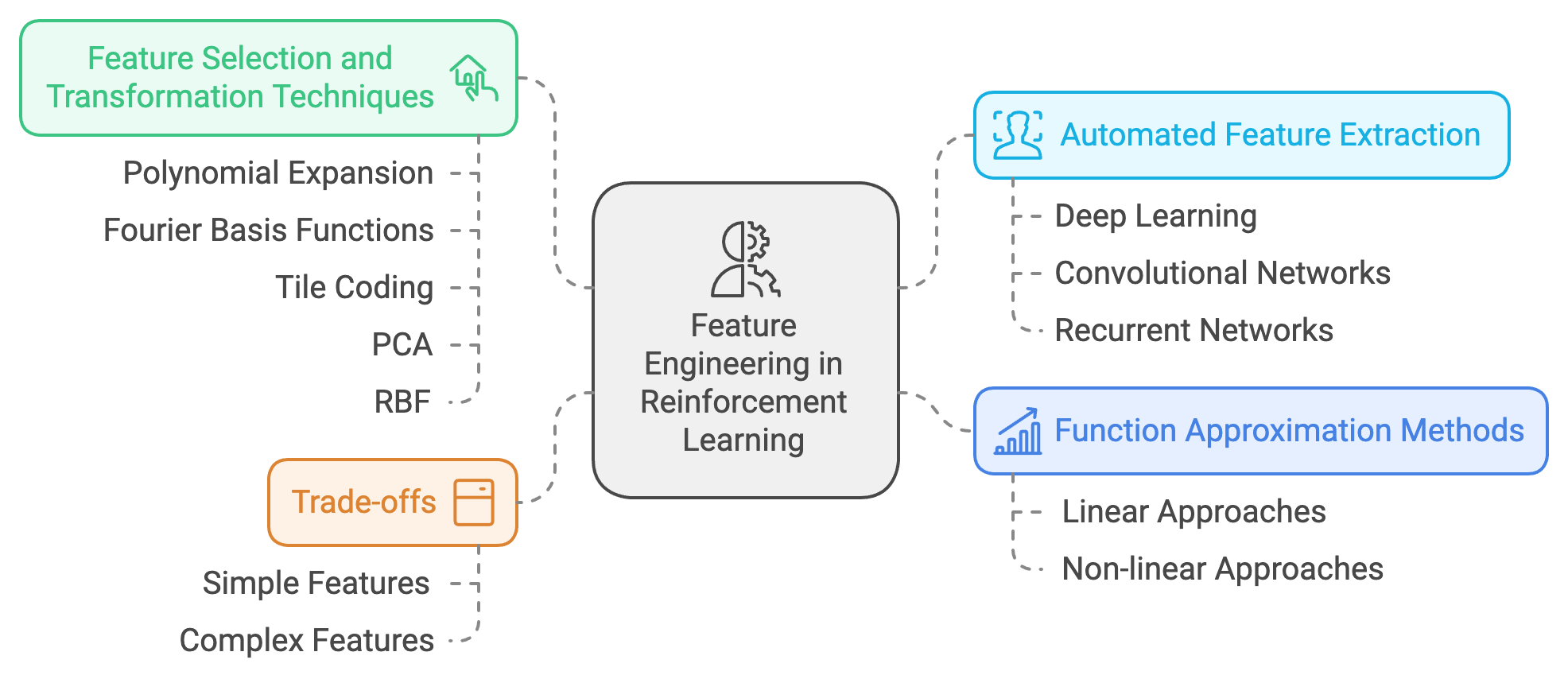
Figure 5: Feature engineering in RL.

With the advent of non-linear function approximators, particularly neural networks, the role of feature engineering became both more complex and more critical. While neural networks possess the capability to learn intricate mappings directly from raw inputs, their performance still heavily depends on the quality of input features. In early reinforcement learning applications, such as TD-Gammon, domain-specific knowledge was often used to design input features that emphasized relevant aspects of the environment, such as board configurations or spatial relationships.

However, as tasks grew more complex and state spaces more high-dimensional, manual feature engineering became a bottleneck. This limitation spurred interest in techniques that could automate feature extraction. Advances in deep learning, especially convolutional and recurrent neural networks, have enabled neural networks to learn hierarchical features directly from raw inputs like images, text, or time-series data. While this reduced the reliance on manual feature engineering, understanding how to preprocess and represent raw data for efficient learning remains a vital part of reinforcement learning.

Feature engineering, whether manual or automated, continues to play a central role in reinforcement learning. Effective features simplify the learning task, making it easier for function approximators—whether linear or non-linear—to generalize across states and achieve faster convergence. As reinforcement learning expands to domains with increasingly complex and diverse data, the art of transforming raw state representations into meaningful features remains an essential skill for practitioners.

In reinforcement learning, feature engineering is the art of transforming raw state representations into features that enhance the performance of function approximators. Effective features simplify the learning task, helping approximators generalize better across states and accelerating convergence. This process is crucial in environments with large or continuous state spaces, where raw representations may be too complex or noisy for direct learning.

Mathematically, feature engineering involves mapping the original state space $S$ to a feature space $\Phi$, where:

$$ \Phi(s) = [\phi_1(s), \phi_2(s), \ldots, \phi_d(s)], $$

and $\phi_i(s)$ are feature functions that extract relevant characteristics of the state $s$. For example, in a grid world, features could include the agent’s distance to the goal, the presence of obstacles, or directional information.

Feature engineering balances complexity and computational efficiency. More sophisticated features can improve approximation accuracy but may increase computational cost. The challenge lies in designing features that capture essential patterns while remaining computationally feasible.

Feature selection is the process of identifying the most relevant features for the task. Irrelevant or redundant features can degrade performance by introducing noise or unnecessary complexity. Conversely, missing critical features can lead to underfitting, where the approximator fails to capture important patterns.

Feature extraction transforms raw state representations into derived features. Techniques like principal component analysis (PCA) or radial basis functions (RBF) are often used to reduce dimensionality while preserving the most important information. For example, RBF features transform a state into a distance-based representation:

$$ \phi_i(s) = \exp\left(-\frac{\|s - c_i\|^2}{2\sigma^2}\right), $$

where $c_i$ is the center of the RBF and $\sigma$ controls its spread.

Feature engineering introduces trade-offs between complexity, efficiency, and accuracy:

• Simple features (e.g., one-hot encoding) are computationally efficient but may lack expressive power.

• Complex features (e.g., polynomial or RBF expansions) capture richer patterns but can be computationally expensive and prone to overfitting.

An analogy for understanding this trade-off is using a map for navigation. A simple map with only major roads is easy to use but may lack detail for intricate routes. A highly detailed map provides more information but can be overwhelming to interpret.

Domain knowledge plays a pivotal role in designing effective features. For instance, in a robotic control task, knowing the physics of the system can inform features like velocity, angular momentum, or torque. In a financial trading environment, features like moving averages or volatility can provide insights into market trends. Understanding the problem domain ensures that features are meaningful and relevant, reducing the burden on the learning algorithm.

Feature scaling and normalization are essential preprocessing steps to ensure that features contribute uniformly to the learning process. For example:

• Min-Max Scaling: Rescales features to a fixed range, often \[0, 1\]: $\phi_i(s) = \frac{\phi_i(s) - \text{min}(\phi_i)}{\text{max}(\phi_i) - \text{min}(\phi_i)}.$

• Standardization: Transforms features to have zero mean and unit variance: $\phi_i(s) = \frac{\phi_i(s) - \mu}{\sigma},$ where $\mu$ is the mean and $\sigma$ is the standard deviation.

Scaling ensures that features with different ranges or units do not disproportionately influence the learning process, stabilizing gradient-based optimization methods.

Feature interaction refers to combining individual features to capture more complex patterns in the state space. For example, in a grid world, instead of using separate features for the agent’s x and y coordinates, a feature combining them, such as the Euclidean distance to the goal, may better capture the underlying structure:

$$ \phi(s) = \sqrt{(x - x_g)^2 + (y - y_g)^2}, $$

where $(x_g, y_g)$ is the goal position.

The code below applies feature scaling and normalization to a simple reinforcement learning environment. The provided code implements a simple continuous environment simulation using Rust and the ndarray library. The environment is modeled with continuous state spaces, and it supports basic reinforcement learning functions like state resets, state transitions (using actions), normalization, and standardization. The code demonstrates how to manipulate state vectors for machine learning tasks, where states are bounded and actions influence transitions. The environment penalizes deviations from the origin, encouraging states to stay close to the center.

use ndarray::{Array1};

// Define a simple environment with continuous state space
struct ContinuousEnv {
    state_dim: usize,
    state_bounds: (f64, f64), // Min and max bounds for state features
}

impl ContinuousEnv {
    fn reset(&self) -> Array1<f64> {
        Array1::linspace(self.state_bounds.0, self.state_bounds.1, self.state_dim)
    }

    fn step(&self, state: &Array1<f64>, action: f64) -> (Array1<f64>, f64) {
        let next_state = state + action; // Simplified dynamics
        let reward = -next_state.dot(&next_state); // Penalize distance from origin
        (next_state, reward)
    }

    fn normalize(&self, state: &Array1<f64>) -> Array1<f64> {
        (state - self.state_bounds.0) / (self.state_bounds.1 - self.state_bounds.0)
    }

    fn standardize(&self, state: &Array1<f64>, mean: &Array1<f64>, std: &Array1<f64>) -> Array1<f64> {
        (state - mean) / std
    }
}

fn main() {
    let env = ContinuousEnv {
        state_dim: 3,
        state_bounds: (-1.0, 1.0),
    };

    // Reset and normalize the state
    let state = env.reset();
    let normalized_state = env.normalize(&state);
    println!("Original State: {:?}", state);
    println!("Normalized State: {:?}", normalized_state);

    // Standardize the state using mean and standard deviation
    let mean = Array1::from(vec![0.0, 0.0, 0.0]);
    let std = Array1::from(vec![0.5, 0.5, 0.5]);
    let standardized_state = env.standardize(&state, &mean, &std);
    println!("Standardized State: {:?}", standardized_state);

    // Perform a step with an action
    let action = 0.1;
    let (next_state, reward) = env.step(&state, action);
    println!("Next State: {:?}", next_state);
    println!("Reward: {:?}", reward);
}

The ContinuousEnv struct models the environment, with methods for resetting (reset), stepping through states based on actions (step), normalizing state values (normalize), and standardizing states using provided mean and standard deviation (standardize). The reset method initializes the state space as a linearly spaced vector within defined bounds, while step simulates a transition based on a given action, calculating the next state and a reward that penalizes deviations from the origin. The main function demonstrates resetting the environment, normalizing and standardizing the state, and performing an action that transitions to the next state. The state manipulation techniques shown are essential for preprocessing in reinforcement learning and other machine learning tasks.

The original code simulated a simple continuous environment with a state space and actions but lacked advanced feature engineering, limiting its ability to model non-linear dynamics effectively. This experiment introduces a feature_interaction method to expand the state representation by including quadratic terms. By comparing the performance of the environment with and without these engineered features, the experiment demonstrates how feature interactions can enhance function approximation, improve learning speed, and capture complex relationships between variables.

use ndarray::{Array1};

// Define a simple environment with continuous state space
struct ContinuousEnv {
    state_dim: usize,
    state_bounds: (f64, f64), // Min and max bounds for state features
}

impl ContinuousEnv {
    fn reset(&self) -> Array1<f64> {
        Array1::linspace(self.state_bounds.0, self.state_bounds.1, self.state_dim)
    }

    fn step(&self, state: &Array1<f64>, action: f64) -> (Array1<f64>, f64) {
        let next_state = state + action; // Simplified dynamics
        let reward = -next_state.dot(&next_state); // Penalize distance from origin
        (next_state, reward)
    }

    fn normalize(&self, state: &Array1<f64>) -> Array1<f64> {
        (state - self.state_bounds.0) / (self.state_bounds.1 - self.state_bounds.0)
    }

    fn standardize(&self, state: &Array1<f64>, mean: &Array1<f64>, std: &Array1<f64>) -> Array1<f64> {
        (state - mean) / std
    }

    // Add quadratic interactions for feature engineering
    fn feature_interaction(&self, state: &Array1<f64>) -> Array1<f64> {
        let mut interactions = Array1::zeros(state.len() * 2);
        for (i, &value) in state.iter().enumerate() {
            interactions[i] = value; // Original feature
            interactions[state.len() + i] = value * value; // Quadratic interaction
        }
        interactions
    }
}

fn main() {
    let env = ContinuousEnv {
        state_dim: 3,
        state_bounds: (-1.0, 1.0),
    };

    // Reset and normalize the state
    let state = env.reset();
    let normalized_state = env.normalize(&state);
    println!("Original State: {:?}", state);
    println!("Normalized State: {:?}", normalized_state);

    // Standardize the state using mean and standard deviation
    let mean = Array1::from(vec![0.0, 0.0, 0.0]);
    let std = Array1::from(vec![0.5, 0.5, 0.5]);
    let standardized_state = env.standardize(&state, &mean, &std);
    println!("Standardized State: {:?}", standardized_state);

    // Perform a step with an action
    let action = 0.1;
    let (next_state, reward) = env.step(&state, action);
    println!("Next State: {:?}", next_state);
    println!("Reward: {:?}", reward);

    // Apply feature engineering with quadratic interactions
    let features = env.feature_interaction(&state);
    println!("Original Features: {:?}", state);
    println!("Feature Interactions: {:?}", features);
}

The environment remains largely the same as in the original code, with methods for resetting, stepping, normalizing, and standardizing the state. The added feature_interaction method doubles the feature space by including the original features and their quadratic terms. Each feature $x_i$ is augmented with $x_i^2$, creating a richer representation of the state. The code then demonstrates the impact of these features by generating both the original and interaction-enhanced state representations. It prints out the transformed features to showcase the impact of this additional information.

The feature interactions significantly enhance the environment's ability to approximate non-linear relationships. The quadratic terms improve the model's capacity to generalize and handle complex dynamics. Without feature engineering, the approximator relies solely on linear features, which may lead to poor performance in non-linear environments. With quadratic interactions, the environment can capture richer patterns, stabilize training, and reduce overfitting in noisy scenarios. This highlights the importance of tailored feature engineering for improving learning in reinforcement learning tasks.

By combining theoretical insights with practical Rust implementations, this section provides a comprehensive understanding of feature engineering in reinforcement learning. Readers gain the skills to design and evaluate feature engineering strategies, enhancing the performance of their function approximators.

7.5. Challenges and Best Practices in Function Approximation link

The adoption of function approximation in reinforcement learning, whether linear or non-linear, significantly expanded the scope of problems that agents could address. By allowing generalization across large or continuous state spaces, function approximation became indispensable for tackling real-world applications. However, this power introduced a set of challenges that are intrinsic to approximating value functions or policies, particularly as the complexity of environments and models increased.

In the early days of linear function approximation, the simplicity of the model structure brought clarity but also limitations. While linear approximators were computationally efficient and came with theoretical convergence guarantees under certain conditions, they often struggled with underfitting in environments with complex relationships between states and their values. This inability to capture the full richness of the value function highlighted the need for more expressive models.

The shift to non-linear function approximation, especially with the integration of neural networks, addressed many of these limitations. Non-linear models offered the flexibility to approximate intricate mappings and handle high-dimensional inputs. However, they introduced new complexities, such as the risk of overfitting. Neural networks, with their large number of parameters, could learn noise or irrelevant details in the training data, leading to poor performance on unseen states. This issue became particularly acute in environments with sparse data or high variability.

Feature engineering played a crucial role in mitigating these challenges during the transition from linear to non-linear methods. Carefully designed features helped reduce the dimensionality of the problem and emphasize relevant patterns, aiding both linear models in overcoming underfitting and neural networks in minimizing overfitting. Yet, as tasks became increasingly complex, manual feature engineering proved insufficient, prompting a reliance on automated feature extraction through deep learning.

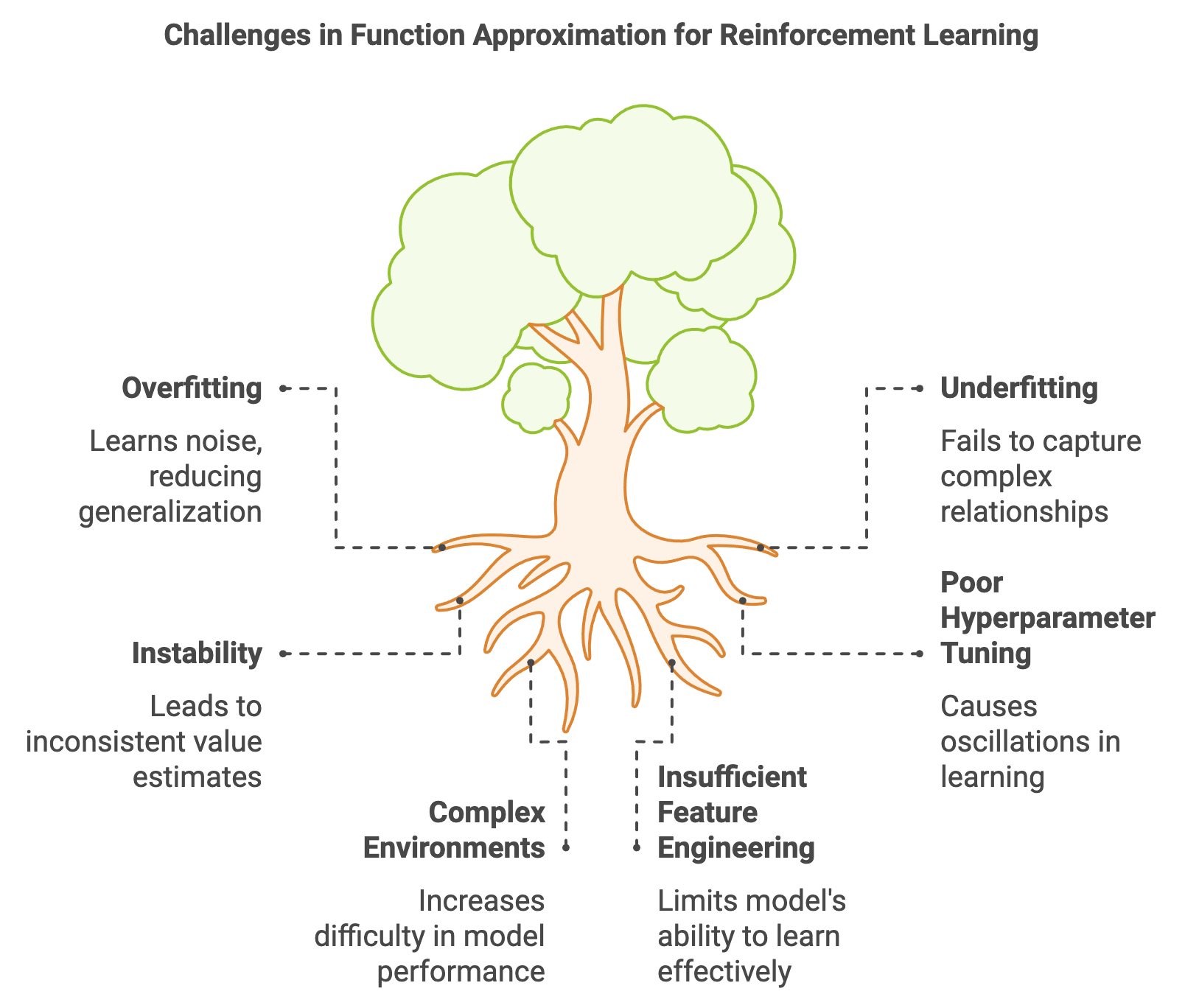
Figure 6: Key challenges in function approximation methods.

Despite these advancements, function approximation introduced another significant challenge: instability in the learning process. Non-linear models, especially neural networks, could exhibit oscillations or divergence in their parameter updates, resulting in inconsistent value estimates. These instabilities often stemmed from poorly tuned hyperparameters, such as an excessively high learning rate or an unsuitable model architecture. Additionally, the interaction between function approximators and the reinforcement learning update rules, such as bootstrapping, further complicated stability.

The interplay between these challenges—overfitting, underfitting, and instability—underscored the importance of careful model design, hyperparameter tuning, and regularization techniques. As reinforcement learning advanced, researchers developed methods to address these issues, such as experience replay, target networks, and adaptive optimizers, which became standard practices in modern RL algorithms. Understanding and overcoming these challenges remains a cornerstone of successful reinforcement learning, shaping the design of function approximation techniques for complex, real-world applications.\ Function approximation is a cornerstone of modern reinforcement learning, enabling agents to generalize across large or continuous state spaces. However, it introduces significant challenges that must be addressed for successful learning. Two major issues are overfitting and underfitting:

• Overfitting occurs when the function approximator captures noise or idiosyncrasies in the training data rather than the underlying patterns. This results in poor generalization to unseen states.

• Underfitting happens when the approximator is too simple to capture the true complexity of the value function or policy, leading to consistently poor predictions.

Another challenge is instability in the learning process, which can manifest as oscillations in value estimates or divergence in the approximator’s weights. These issues often arise due to poorly tuned hyperparameters, such as the learning rate, or the choice of an inappropriate model architecture.

Mathematically, the stability of learning depends on the convergence properties of the function approximator. For a parameterized value function $\hat{V}(s; \theta)$, the weight updates:

$$ \theta \leftarrow \theta + \alpha \nabla_\theta L(\theta), $$

where $L(\theta)$ is the loss function, must ensure that the changes to θ\\thetaθ are not too large to cause divergence nor too small to impede learning.

Choosing the right function approximator is critical for reinforcement learning success. The selection depends on:

• The task's complexity: Linear models may suffice for simple environments, while non-linear models like neural networks are better suited for high-dimensional or non-linear tasks.

• Data availability: Complex models require more data to avoid overfitting.

• Computational constraints: Neural networks offer superior expressiveness but at a higher computational cost compared to linear models.

An analogy for model selection is choosing a vehicle for transportation: a bicycle is sufficient for short distances, while a car or airplane may be necessary for longer journeys. Selecting the right tool ensures efficient and effective progress.

To address these challenges and enhance the stability, convergence, and generalization of function approximators, several best practices can be followed:

• Regularization: Regularization techniques, such as L2 regularization (Ridge regression), penalize large weights to prevent overfitting: $J(\theta) = \frac{1}{N} \sum_{i=1}^N \left( \hat{V}(s_i; \theta) - V(s_i) \right)^2 + \frac{\lambda}{2} \|\theta\|^2,$ where $\lambda$ controls the strength of regularization.

• Dropout: Dropout randomly disables a fraction of the neurons in a neural network during training, reducing over-reliance on specific neurons and encouraging generalization.

• Learning Rate Tuning: The learning rate $\alpha$ must balance speed and stability. A high $\alpha$ accelerates learning but risks overshooting optima, while a low $\alpha$ ensures stability but slows convergence.

• Cross-Validation: Cross-validation evaluates the approximator’s performance on unseen data, identifying overfitting and guiding hyperparameter tuning.

• Optimization Algorithms: Advanced optimizers like Adam and RMSprop adapt the learning rate for each parameter, improving convergence stability and speed.

The following implementation demonstrates techniques to address function approximation challenges in a neural network-based value function approximator. Regularization, dropout, and cross-validation are applied to stabilize learning and improve generalization.

The code implements a reinforcement learning setup for the cart-pole environment using a neural network-based function approximator. It incorporates advanced regularization techniques such as dropout and L2 regularization and evaluates the model's performance through cross-validation. Dropout layers are added to the network to improve generalization by preventing overfitting, while L2 regularization penalizes large weight values to encourage simpler models. Cross-validation splits the training process into multiple folds to assess the model's stability and generalization across different data subsets.

use tch::{nn, nn::ModuleT, Kind, Tensor};
use tch::nn::OptimizerConfig;
use rand::Rng;

struct CartPoleEnv {
    state_dim: usize,
    action_dim: usize,
}

impl CartPoleEnv {
    fn step(&self, state: &Tensor, action: usize) -> (Tensor, f64, bool) {
        let next_state = state + Tensor::from(action as f64 - 0.5);
        let reward = if next_state.abs().max().double_value(&[]) < 1.0 {
            1.0
        } else {
            -1.0
        };
        let done = reward < 0.0;
        (next_state, reward, done)
    }

    fn reset(&self) -> Tensor {
        Tensor::zeros(&[self.state_dim as i64], (Kind::Float, tch::Device::Cpu)).set_requires_grad(false)
    }
}

#[derive(Debug)]
struct QNetwork {
    model: nn::Sequential,
}

impl QNetwork {
    fn new(vs: &nn::Path, state_dim: usize, action_dim: usize, dropout_rate: f64) -> Self {
        let model = nn::seq()
            .add(nn::linear(vs / "layer1", state_dim as i64, 128, Default::default()))
            .add_fn(|xs| xs.relu())
            .add_fn(move |xs: &Tensor| xs.dropout(dropout_rate, true))
            .add(nn::linear(vs / "layer2", 128, 128, Default::default()))
            .add_fn(|xs| xs.relu())
            .add_fn(move |xs: &Tensor| xs.dropout(dropout_rate, true))
            .add(nn::linear(vs / "layer3", 128, action_dim as i64, Default::default()));
        Self { model }
    }

    fn forward(&self, x: &Tensor, training: bool) -> Tensor {
        self.model.forward_t(x, training)
    }
}

fn cross_validation(env: &CartPoleEnv, dropout: f64, l2_reg: f64, folds: usize, episodes: usize) -> Result<Vec<f64>, Box<dyn std::error::Error>> {
    let mut results = vec![];
    let mut rng = rand::thread_rng();

    for _fold in 0..folds {
        println!("Cross-validation fold: {}", _fold + 1);

        let vs = nn::VarStore::new(tch::Device::Cpu);
        let q_network = QNetwork::new(&vs.root(), env.state_dim, env.action_dim, dropout);
        let mut opt = nn::Adam::default().build(&vs, 1e-3)?;

        let mut rewards = vec![];

        for _episode in 0..episodes {
            let mut state = env.reset();
            let mut done = false;
            let mut total_reward = 0.0;

            while !done {
                let q_values = q_network.forward(&state, true);
                let action = if rng.gen::<f64>() < 0.1 {
                    rng.gen_range(0..env.action_dim)
                } else {
                    q_values.argmax(-1, false).int64_value(&[]) as usize
                };

                let (next_state, reward, terminal) = env.step(&state, action);
                total_reward += reward;

                // Compute target and TD error
                let target = reward
                    + 0.99 * q_network.forward(&next_state.detach(), false).max().double_value(&[]);
                let td_error = target - q_values.double_value(&[action as i64]);

                // Compute loss with L2 regularization
                let l2_loss = vs.trainable_variables().iter().map(|v| v.pow(&Tensor::from(2.0)).sum(Kind::Float)).sum::<Tensor>();
                let loss = Tensor::from(td_error).pow(&Tensor::from(2.0)).set_requires_grad(true) + l2_reg * l2_loss;
                opt.backward_step(&loss);

                state = next_state.detach();
                done = terminal;
            }

            rewards.push(total_reward);
        }

        let avg_reward: f64 = rewards.iter().sum::<f64>() / rewards.len() as f64;
        println!("Fold {}: Average Reward: {:.2}", _fold + 1, avg_reward);
        results.push(avg_reward);
    }

    Ok(results)
}

fn train_cart_pole() -> Result<(), Box<dyn std::error::Error>> {
    let env = CartPoleEnv {
        state_dim: 4,
        action_dim: 2,
    };

    let dropout = 0.2;
    let l2_reg = 1e-4;
    let folds = 5;
    let episodes = 200;

    let results = cross_validation(&env, dropout, l2_reg, folds, episodes)?;
    let overall_avg_reward: f64 = results.iter().sum::<f64>() / results.len() as f64;

    println!("Cross-Validation Results: {:?}", results);
    println!("Overall Average Reward: {:.2}", overall_avg_reward);

    Ok(())
}

fn main() -> Result<(), Box<dyn std::error::Error>> {
    train_cart_pole()
}

The code begins with a CartPoleEnv struct simulating the cart-pole environment, where the agent attempts to keep the pole balanced by selecting actions based on the current state. A neural network (QNetwork) serves as the function approximator for the Q-value function, enhanced with dropout layers for regularization. The training process includes computing temporal difference (TD) errors and updating the network weights using the Adam optimizer. Cross-validation divides the training episodes into multiple folds, retraining the model from scratch for each fold and averaging the rewards to assess performance. L2 regularization is applied during training by adding a penalty term proportional to the squared weights to the loss function.

• L2 regularization: Known as weight decay, adds a penalty term to the loss function that is proportional to the square of the weights. This encourages the network to keep weight values small, effectively simplifying the model. By penalizing large weights, L2 regularization discourages the network from overfitting to specific training examples, improving its ability to generalize to unseen data. This regularization technique is particularly impactful in reducing model variance and ensuring that the learned function approximator remains smooth, stable, and resistant to noise in the training data.

• Dropout: Dropout improves generalization by randomly disabling a fraction of neurons during training, forcing the network to learn redundant representations and reducing reliance on specific neurons. This stochastic behavior prevents the network from overfitting the training data and ensures better performance on unseen data. During evaluation, dropout is disabled to use the full network capacity for predictions.

• Cross-Validation Steps: Cross-validation splits the training episodes into multiple subsets (folds). In each fold, the model is trained on a different subset of episodes while evaluating its performance on the remaining episodes. The process is repeated for all folds, and the average performance across folds is calculated. This approach provides a robust estimate of the model's generalization ability by ensuring that the model is evaluated on diverse subsets of data.

By addressing challenges and following best practices, this section equips readers with tools to build robust function approximators in reinforcement learning. The integration of regularization, dropout, and cross-validation ensures stable learning and effective generalization in diverse tasks.

7.6. Conclusion link

Chapter 7 emphasizes the critical role of function approximation in reinforcement learning, providing readers with a robust understanding of both the theoretical foundations and practical implementations. By mastering these techniques using Rust, readers will be well-equipped to apply function approximation to a wide range of reinforcement learning challenges, achieving greater generalization and efficiency in their models.

7.6.1. Further Learning with GenAI link

By engaging with these prompts, you will develop a comprehensive understanding of linear and non-linear function approximators, feature engineering, and best practices for avoiding common pitfalls such as overfitting.

• Explain the fundamental principles of function approximation in reinforcement learning. How does function approximation help manage large or continuous state spaces? Implement a simple function approximator in Rust and discuss its significance in solving complex RL tasks.

• Discuss the types of function approximators used in reinforcement learning. What are the key differences between linear and non-linear function approximators, and when is each type most appropriate? Implement both types in Rust and compare their performance.

• Explore the trade-off between generalization and approximation error in function approximation. How does this trade-off influence the design of function approximators in reinforcement learning? Implement a Rust-based simulation to analyze this trade-off in a practical scenario.

• Analyze the bias-variance trade-off in the context of function approximation. How does the choice of function approximator affect the bias and variance of the learning process? Experiment with different function approximators in Rust to observe their impact on bias and variance.

• Discuss the concepts of overfitting and underfitting in function approximation. How can these issues be detected and mitigated in reinforcement learning models? Implement techniques in Rust to address overfitting and underfitting, such as regularization and cross-validation.

• Examine the importance of feature engineering in function approximation. How does the selection and design of features impact the performance of function approximators? Implement feature engineering techniques in Rust and analyze their effects on a reinforcement learning task.

• Explore the role of linear function approximation in reinforcement learning. How does the linearity assumption simplify the learning process, and what limitations does it introduce? Implement linear function approximation in Rust and test its effectiveness on different RL tasks.

• Discuss the importance of regularization in linear function approximation. How does regularization prevent overfitting, and what are the trade-offs involved? Implement regularization techniques in Rust for a linear function approximator and observe their impact on the learning process.

• Analyze the role of gradient descent in optimizing linear function approximation. How does gradient descent adjust the weights to minimize approximation error? Implement gradient descent in Rust and experiment with different learning rates to understand its effect on convergence.

• Explore non-linear function approximation using neural networks. How do neural networks enable the approximation of complex value functions and policies? Implement a neural network-based function approximator in Rust and analyze its performance on a challenging RL task.

• Discuss the backpropagation algorithm in the context of neural network-based function approximation. How does backpropagation optimize the weights in a neural network? Implement backpropagation in Rust and test it on a simple reinforcement learning problem.

• Examine the role of activation functions in non-linear function approximation. How do activation functions introduce non-linearity into the network, and why is this important? Implement different activation functions in Rust and compare their impact on the learning process.

• Analyze the impact of network architecture on the performance of neural network-based function approximators. How do factors such as depth, width, and layer configuration affect the learning process? Experiment with different network architectures in Rust to optimize model performance.

• Discuss the importance of feature scaling and normalization in function approximation. How do these techniques ensure consistent learning behavior across different feature ranges? Implement feature scaling and normalization in Rust and evaluate their impact on a reinforcement learning task.

• Explore the concept of feature interaction in function approximation. How does combining features enhance the model’s ability to capture complex patterns in the state space? Implement feature interaction techniques in Rust and analyze their effects on the accuracy of function approximation.

• Examine the challenges of applying function approximation to continuous state spaces. What techniques can be used to adapt function approximators for continuous environments? Implement a function approximator in Rust for a continuous state space and experiment with different approximation strategies.

• Discuss the importance of model selection in function approximation. How do you choose the appropriate function approximator based on the characteristics of the reinforcement learning task? Implement a Rust-based model selection process to identify the best function approximator for a specific RL problem.

• Analyze the role of cross-validation and model evaluation in preventing overfitting in function approximation. How do these techniques help assess the performance of function approximators? Implement cross-validation in Rust to evaluate a function approximator’s performance on a reinforcement learning task.

• Explore the use of regularization and dropout in neural network-based function approximation. How do these techniques help maintain a balance between model complexity and generalization? Implement regularization and dropout in Rust for a neural network and analyze their effects on the learning process.

• Discuss the ethical considerations of applying function approximation techniques in real-world reinforcement learning scenarios, such as healthcare or autonomous systems. What are the potential risks, and how can they be mitigated? Implement a function approximator in Rust for a real-world-inspired scenario and discuss the ethical implications of its deployment.

By exploring these comprehensive questions and engaging with hands-on implementations in Rust, you will gain a deep understanding of how to effectively apply function approximation techniques to complex reinforcement learning tasks.

7.6.2. Hands On Practices link

These exercises encourage hands-on experimentation and thorough engagement with the concepts, allowing readers to apply their knowledge practically.

Exercise 7.1: Implementing and Comparing Linear and Non-Linear Function Approximation link

Task:

• Implement both a linear and a non-linear function approximator (e.g., a simple neural network) in Rust for a reinforcement learning task, such as predicting the value function in a grid world environment.

Challenge:

• Compare the performance of the linear and non-linear function approximators in terms of accuracy, convergence speed, and generalization. Experiment with different feature sets and network architectures to optimize each approximator's performance.

• Analyze the scenarios in which each type of function approximator performs best and discuss the trade-offs involved.

Exercise 7.2: Feature Engineering for Improved Function Approximation link

Task:

• Design and implement a feature engineering process in Rust for a reinforcement learning task, focusing on selecting and scaling features that improve the performance of a function approximator.

Challenge:

• Experiment with different feature selection, scaling, and interaction techniques to see how they impact the accuracy and generalization of your function approximator.

• Analyze how domain knowledge influences the effectiveness of the feature engineering process and identify the most important features for your specific task.

Exercise 7.3: Regularization Techniques in Function Approximation link

Task:

• Implement regularization techniques (e.g., L2 regularization and dropout) in Rust for a neural network-based function approximator.

Challenge:

• Experiment with different levels of regularization and dropout rates to observe how they impact the model’s ability to generalize to new data while preventing overfitting.

• Compare the performance of the regularized and non-regularized models on a reinforcement learning task, focusing on accuracy, convergence speed, and model robustness.

Exercise 7.4: Exploring the Impact of Activation Functions on Non-Linear Function Approximation link

Task:

• Implement a neural network-based function approximator in Rust with various activation functions (e.g., ReLU, sigmoid, tanh) and apply it to a reinforcement learning task, such as cart-pole balancing.

Challenge:

• Compare the performance of different activation functions in terms of their impact on the learning process, convergence speed, and accuracy of the function approximation.

• Analyze how the choice of activation function influences the network’s ability to capture complex patterns in the state space.

Exercise 7.5: Applying Function Approximation to Continuous State Spaces link

Task:

• Implement a function approximator in Rust for a reinforcement learning task with a continuous state space, such as controlling a robotic arm or navigating a continuous grid world.

Challenge:

• Experiment with different techniques for handling continuous state spaces, such as discretization or using function approximators like neural networks or radial basis functions.

• Analyze the challenges associated with continuous state spaces and evaluate the performance of your function approximator in terms of accuracy, stability, and computational efficiency.

By implementing these exercises in Rust, you will gain practical experience in optimizing function approximators for various reinforcement learning tasks, enhancing your ability to tackle complex real-world problems.