Chapter 8
Eligibility Traces
"Eligibility traces provide a powerful mechanism for balancing the immediacy of temporal-difference learning with the long-term perspective of Monte Carlo methods." — Richard Sutton
Chapter 8 of RLVR delves into the advanced concept of eligibility traces, a powerful mechanism that bridges the gap between Temporal-Difference (TD) methods and Monte Carlo methods in reinforcement learning. The chapter begins with an introduction to eligibility traces, explaining how they assign credit to states based on their recency and frequency of visits, and the crucial role of the decay parameter (λ) in controlling trace influence. Readers will explore the differences between accumulating and replacing traces, understanding how these strategies affect learning dynamics and policy improvement. The chapter then expands on TD(λ), showing how it generalizes other reinforcement learning algorithms by balancing short-term and long-term learning through eligibility traces. A detailed comparison of the forward and backward views provides insights into the conceptual and practical differences in how eligibility traces propagate credit and update states. The chapter concludes by addressing the challenges and best practices in using eligibility traces, emphasizing the importance of tuning λ, managing trace decay, and ensuring stability in learning. Through hands-on Rust implementations, readers will learn to apply, experiment with, and optimize eligibility traces in various reinforcement learning scenarios, enhancing both their understanding and practical skills in this sophisticated aspect of RL.
8.1. Introduction to Eligibility Traces
The development of eligibility traces in reinforcement learning stems from the challenge of effective credit assignment across time. In sequential decision-making tasks, an agent must determine which past states and actions contributed to a future reward. This problem is fundamental to reinforcement learning and has been approached through different paradigms, notably Temporal-Difference (TD) and Monte Carlo methods.
Monte Carlo methods were among the first model-free approaches to address credit assignment. By observing complete episodes, these methods attributed credit based on the total return from an episode, providing unbiased estimates. However, Monte Carlo methods require waiting until the end of an episode to update values, which is inefficient for tasks with long or continuous episodes. Temporal-Difference (TD) methods, introduced by Richard Sutton in 1988, addressed this inefficiency by using bootstrapping—updating values incrementally based on immediate transitions and current estimates of future values. While efficient, TD methods focus on short-term dependencies, often updating value functions based only on the most recent transitions.
Figure 1: The historical evolution journey of credit assignment in RL.
The limitations of these two approaches motivated the development of a framework that could combine their strengths. Researchers recognized that an ideal credit assignment mechanism would incorporate both short-term feedback and long-term contributions, enabling more comprehensive and efficient learning. This led to the concept of eligibility traces, introduced as a way to extend TD learning by maintaining a memory of visited states and actions.
Eligibility traces introduced a decay mechanism that weighted past states based on their recency and frequency of visits. This allowed updates to propagate rewards not just to the most recent state but to all states that had contributed to the outcome. By doing so, eligibility traces created a continuum between TD and Monte Carlo methods, controlled by a parameter $\lambda$. For $\lambda = 0$, the approach reduces to standard TD(0) with one-step updates, while $\lambda = 1$ corresponds to Monte Carlo methods, considering entire episodes.
This unification proved particularly useful for tasks with delayed rewards or sparse feedback, where the relationships between states and outcomes spanned multiple steps. The introduction of eligibility traces enabled reinforcement learning algorithms to assign credit more effectively, improving convergence rates and stability in various domains.
Eligibility traces have become a cornerstone of reinforcement learning, underpinning key algorithms such as TD(λ), SARSA(λ), and Actor-Critic methods. Their unique ability to balance short-term and long-term learning makes them invaluable for addressing complex, real-world tasks characterized by temporal dependencies. By providing a unified mechanism that combines the strengths of Temporal-Difference (TD) and Monte Carlo methods, eligibility traces enable more effective credit assignment. They allow algorithms to assign credit not only based on immediate feedback but also by considering the recency and frequency of state visits. This facilitates a more efficient learning process, seamlessly bridging the gap between the short-term updates of TD methods and the long-term horizon of Monte Carlo methods, making eligibility traces a versatile tool for reinforcement learning tasks.
Mathematically, an eligibility trace is a scalar value associated with each state (or state-action pair) that tracks how eligible it is for updates. Eligibility traces are updated at each time step as follows:
$$E_t(s) = \gamma \lambda E_{t-1}(s) + \mathbf{1}(S_t = s),$$
where:
$E_t(s)$ is the eligibility trace for state $s$ at time $t$,
$\gamma$ is the discount factor,
$\lambda$ is the trace decay parameter, controlling how quickly traces fade,
$\mathbf{1}(S_t = s)$ is an indicator function that is 1 if state $s$ is visited at time $t$, otherwise 0.
The eligibility trace acts as a memory of past visits to states, decaying over time unless reinforced by repeated visits. This decay mechanism ensures that recent states are prioritized while allowing the algorithm to consider longer-term dependencies.
Eligibility traces address a fundamental challenge in reinforcement learning: how to efficiently propagate credit for rewards across multiple states and actions. By assigning a non-zero trace value to states visited in the past, the algorithm can update these states even when they are not immediately involved in the current transition. The key advantage is that eligibility traces allow learning to incorporate information from multiple steps into a single update, improving both stability and convergence speed.
The trace decay parameter $\lambda$ plays a pivotal role in controlling the balance between immediate and long-term credit assignment:
When $\lambda = 0$, the algorithm reduces to TD(0), which focuses solely on the most recent transition.
When $\lambda = 1$, the algorithm approximates Monte Carlo methods, incorporating the entire episode's return.
This flexibility makes eligibility traces a unifying framework for reinforcement learning algorithms, enabling practitioners to adapt the learning process to the specific characteristics of their tasks.
There are two common ways to maintain eligibility traces: accumulating traces and replacing traces:
Accumulating traces: Eligibility traces accumulate with each visit to a state: $E_t(s) = \gamma \lambda E_{t-1}(s) + 1.$ This approach increases the credit for states that are revisited multiple times.
Replacing traces: Eligibility traces are reset to 1 upon each visit: $E_t(s) = 1 + \gamma \lambda E_{t-1}(s) \cdot \mathbf{1}(S_t \neq s).$ This approach ensures that the most recent visit dominates the trace value.
TD(λ) seamlessly transitions between TD(0) and Monte Carlo methods by varying $\lambda$. For intermediate values of $\lambda$, TD(λ) blends the short-term focus of TD(0) with the long-term perspective of Monte Carlo, offering a flexible and efficient learning strategy.
Eligibility traces generalize the concept of n-step TD methods. By maintaining a continuous memory of past states, they eliminate the need to specify a fixed step size $n$, providing a smoother and more adaptable approach to reinforcement learning.
The code below implements a reinforcement learning algorithm, TD Learning with eligibility traces (TD(λ)), to estimate the value function of a grid world environment. The grid world is a simple 5x5 grid where the agent starts at the top-left corner and tries to reach the goal state at the bottom-right corner. The value function is learned through random actions, with rewards given for reaching the goal and penalties otherwise. Additionally, the code visualizes the learned value function as a heatmap, enabling easy interpretation of the agent's understanding of the environment.
use plotters::prelude::*;
use std::collections::HashMap;
use rand::Rng; // For random number generation
// Define the grid world environment
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => ((state.0 + 1).min(self.size - 1), state.1), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 };
(next_state, reward)
}
}
// TD(λ) implementation with eligibility traces
fn td_lambda(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
for episode in 0..episodes {
println!("Episode: {}", episode + 1);
let mut state = (0, 0); // Start at top-left corner
let mut episode_states = vec![state];
while state != grid_world.goal_state {
let action = rand::thread_rng().gen_range(0..4); // Random action
let (next_state, reward) = grid_world.step(state, action);
let current_value = *value_function.get(&state).unwrap_or(&0.0);
let next_value = *value_function.get(&next_state).unwrap_or(&0.0);
let td_error = reward + gamma * next_value - current_value;
// Update eligibility traces
for s in &episode_states {
let trace = eligibility_traces.entry(*s).or_insert(0.0);
*trace *= gamma * lambda;
}
*eligibility_traces.entry(state).or_insert(0.0) += 1.0;
// Update value function
for (s, trace) in &eligibility_traces {
let v = value_function.entry(*s).or_insert(0.0);
*v += alpha * td_error * trace;
}
state = next_state;
episode_states.push(state);
}
// Decay eligibility traces
for trace in eligibility_traces.values_mut() {
*trace *= gamma * lambda;
}
}
value_function
}
// Visualize the value function as a heatmap
fn visualize_value_function(
value_function: &HashMap<(usize, usize), f64>,
grid_size: usize,
output_path: &str,
) -> Result<(), Box<dyn std::error::Error>> {
let root = BitMapBackend::new(output_path, (600, 600)).into_drawing_area();
root.fill(&WHITE)?;
let max_value = value_function.values().cloned().fold(f64::MIN, f64::max);
let min_value = value_function.values().cloned().fold(f64::MAX, f64::min);
let mut chart = ChartBuilder::on(&root)
.caption("Value Function Heatmap", ("sans-serif", 20))
.margin(20)
.x_label_area_size(20)
.y_label_area_size(20)
.build_cartesian_2d(0..grid_size, 0..grid_size)?;
chart.configure_mesh().disable_mesh().draw()?;
for x in 0..grid_size {
for y in 0..grid_size {
let value = *value_function.get(&(x, y)).unwrap_or(&0.0);
let intensity = (value - min_value) / (max_value - min_value);
let color = HSLColor(0.6 - intensity * 0.6, 1.0, 0.5);
chart.draw_series(std::iter::once(Rectangle::new(
[(x, y), (x + 1, y + 1)],
color.filled(),
)))?;
}
}
root.present()?;
println!("Heatmap saved to {}", output_path);
Ok(())
}
fn main() -> Result<(), Box<dyn std::error::Error>> {
let grid_world = GridWorld {
size: 5,
goal_state: (4, 4),
};
let episodes = 500;
let alpha = 0.1;
let gamma = 0.9;
let lambda = 0.5;
let value_function = td_lambda(&grid_world, episodes, alpha, gamma, lambda);
println!("\nLearned Value Function:");
for (state, value) in value_function.iter() {
println!("State {:?}: {:.2}", state, value);
}
// Visualize the value function
visualize_value_function(&value_function, grid_world.size, "value_function_heatmap.png")?;
Ok(())
}
The GridWorld struct defines the environment, including the size, goal state, and the logic for moving within the grid. The td_lambda function uses TD(λ) with random actions to iteratively update the value function for each state. This is achieved by calculating temporal difference errors and adjusting the values based on eligibility traces, which track how frequently states are visited during an episode. After multiple episodes, the algorithm approximates the value function for all states, showing how close they are to the goal. The learned values are stored in a hashmap, with states as keys and their respective values as values.
Figure 2: Plotters visualization of value function heatmap.
The visualization renders the value function as a heatmap using the plotters crate. Each grid cell corresponds to a state, and its color intensity reflects the value of that state. Higher values (indicating states closer to the goal) appear in brighter or more saturated hues, while lower values appear dimmer. This heatmap provides an intuitive understanding of the agent's learned policy, showing how the environment's structure and rewards influence the agent's value estimates. The resulting heatmap is saved as an image file (value_function_heatmap.png) for further analysis or presentation.
The revised code extends the original version by incorporating an experiment that evaluates the effect of varying the λ (lambda) parameter in TD(λ) learning on a grid world environment. Lambda controls the balance between Monte Carlo and temporal difference (TD) updates, with λ=0 relying purely on TD learning and λ=1 representing Monte Carlo methods. The experiment computes value functions for λ values of 0.0, 0.5, and 1.0, runs the learning process for each λ, and visualizes the resulting value functions as heatmaps. The heatmaps provide a visual comparison of how different λ values influence the learned value distribution across the grid.
use plotters::prelude::*;
use std::collections::HashMap;
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Up
1 => (state.0 + 1, state.1.min(self.size - 1)), // Down
2 => (state.0, state.1.saturating_sub(1)), // Left
_ => (state.0, state.1 + 1.min(self.size - 1)), // Right
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 };
(next_state, reward)
}
}
fn td_lambda(
grid_world: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
for episode in 0..episodes {
let mut state = (0, 0);
let mut episode_states = vec![state];
println!("Starting episode {} with state {:?}", episode + 1, state);
while state != grid_world.goal_state {
let action = rand::random::<usize>() % 4;
let (next_state, reward) = grid_world.step(state, action);
let td_error = reward
+ gamma * *value_function.get(&next_state).unwrap_or(&0.0)
- *value_function.get(&state).unwrap_or(&0.0);
println!("State: {:?}, Action: {}, Next State: {:?}, Reward: {:.2}, TD Error: {:.4}", state, action, next_state, reward, td_error);
for s in episode_states.iter() {
let trace = eligibility_traces.entry(*s).or_insert(0.0);
*trace = gamma * lambda * *trace;
}
*eligibility_traces.entry(state).or_insert(0.0) += 1.0;
for (s, trace) in &eligibility_traces {
let v = value_function.entry(*s).or_insert(0.0);
*v += alpha * td_error * trace;
}
state = next_state;
episode_states.push(state);
}
for trace in eligibility_traces.values_mut() {
*trace *= gamma * lambda;
}
}
value_function
}
fn visualize_heatmaps(
value_functions: Vec<(f64, HashMap<(usize, usize), f64>)>,
grid_size: usize,
output_file: &str,
) -> Result<(), Box<dyn std::error::Error>> {
let root = BitMapBackend::new(output_file, (800, 300)).into_drawing_area();
root.fill(&WHITE)?;
let num_maps = value_functions.len();
let mut chart = ChartBuilder::on(&root)
.caption("Value Function Heatmaps for Different λ Values", ("sans-serif", 20))
.build_cartesian_2d(0..grid_size * num_maps, 0..grid_size)?;
chart.configure_mesh().disable_mesh().draw()?;
for (i, (lambda, value_function)) in value_functions.iter().enumerate() {
println!("Visualizing value function for λ = {}", lambda);
for x in 0..grid_size {
for y in 0..grid_size {
let value = *value_function.get(&(x, y)).unwrap_or(&0.0);
let color = HSLColor(240.0 - value * 20.0, 1.0, 0.5).to_rgba();
chart
.draw_series(std::iter::once(Rectangle::new(
[
(x + i * grid_size, y),
(x + i * grid_size + 1, y + 1),
],
color.filled(),
)))?;
}
}
}
root.present()?;
Ok(())
}
fn main() -> Result<(), Box<dyn std::error::Error>> {
let grid_world = GridWorld {
size: 5,
goal_state: (4, 4),
};
let episodes = 500;
let alpha = 0.1;
let gamma = 0.9;
let mut value_functions = vec![];
for &lambda in &[0.0, 0.5, 1.0] {
println!("\nTraining with λ = {}", lambda);
let value_function = td_lambda(&grid_world, episodes, alpha, gamma, lambda);
value_functions.push((lambda, value_function));
}
visualize_heatmaps(value_functions, grid_world.size, "value_function_heatmaps.png")?;
println!("Heatmaps saved to value_function_heatmaps.png");
Ok(())
}
The heatmaps reveal that the choice of λ significantly impacts the quality and convergence of the learned value function. For λ=0.0 (pure TD), the value function typically converges faster but may be less accurate for states further from the goal, as TD updates are more local. For λ=1.0 (Monte Carlo), the values are more consistent across the grid, reflecting better propagation of information from the goal, but convergence can be slower due to reliance on full episodes. λ=0.5 balances these extremes, often providing a good trade-off between accuracy and convergence speed. The experiment underscores the importance of tuning λ based on the problem's characteristics to achieve optimal learning.
This section equips RLVR readers with a comprehensive understanding of eligibility traces and their role in reinforcement learning. The theoretical foundations and practical Rust implementations highlight the flexibility and power of TD(λ) in diverse tasks.
8.2. Accumulate vs. Replace Eligibility Traces
The introduction of eligibility traces extended the flexibility of TD methods, leading to the development of algorithms like TD(λ) and SARSA(λ). A key aspect of this framework is how eligibility traces are updated during learning. Unlike simple TD updates that focus on a single state, eligibility traces allow updates to cascade across many states, depending on how recently they were visited. This capability introduces additional considerations for how traces should decay or reset during the learning process. Two common strategies, accumulate traces and replace traces, were developed to handle this decay. These strategies differ in how they manage overlapping updates, influencing the stability and speed of convergence in reinforcement learning algorithms.
Figure 3: The scopes and hierarchy of eligibility traces in RL.
Eligibility traces are a powerful mechanism in reinforcement learning, assigning credit to past states based on their recency and frequency of visits. The way these traces are updated has a significant impact on the learning dynamics of algorithms like TD(λ). Two common strategies for updating eligibility traces are accumulate traces and replace traces, each with its strengths and weaknesses.
Accumulating traces allow the eligibility of a state to build up over time. Each time a state is revisited within an episode, its eligibility trace increases, reflecting its repeated contribution to the outcome. This approach emphasizes states that are frequently revisited, which can be advantageous in tasks where certain states play a recurring role in achieving rewards.
Replacing traces, on the other hand, reset the eligibility trace of a state to its maximum value whenever it is visited. Instead of accumulating contributions, the trace reflects only the most recent visit, ensuring that the latest information about the state has the greatest impact. This approach is often more stable in tasks where overemphasizing frequent visits could lead to instability.
In the accumulating strategy, the eligibility trace for a state $s$ at time $t$ is updated as:
$$ E_t(s) = \gamma \lambda E_{t-1}(s) + 1, $$
where:
$\gamma$ is the discount factor,
$\lambda$ is the decay parameter,
$E_t(s)$ is the eligibility trace at time ttt.
This formula increases the trace value at each visit while allowing previous contributions to decay exponentially. In the replacing strategy, the eligibility trace for a state $s$ is reset to 1 on every visit:
$$ E_t(s) = \begin{cases} 1 & \text{if } s \text{ is visited at } t, \\ \gamma \lambda E_{t-1}(s) & \text{otherwise}. \end{cases} $$
This approach ensures that only the most recent visit determines the state’s contribution, avoiding the potential for runaway trace values. The choice between accumulate and replace strategies affects the behavior and stability of TD(λ):
Accumulating traces are better suited for tasks with recurring state visits where repeated emphasis is beneficial, such as grid worlds or cyclic tasks. However, they may lead to instability if certain states dominate the learning process.
Replacing traces are more stable in environments where overemphasizing state visits could disrupt learning, such as continuous control tasks or environments with rapidly changing dynamics.
Understanding accumulating and replacing traces in reinforcement learning can be likened to managing a queue of tasks. Accumulating traces function like adding priority to tasks every time they are revisited, emphasizing their importance repeatedly. In contrast, replacing traces ensure that only the most recent priority is considered, focusing on the latest interaction with a task.
The choice between these strategies depends on the characteristics of the task. Accumulating traces are advantageous in scenarios where certain states are critical and frequently revisited, as they enable faster learning by amplifying the contributions of these states. Conversely, replacing traces offer greater stability in environments where overemphasis on specific states could lead to misleading updates and potentially hinder learning.
The impact of these strategies on policy improvement lies in how they propagate credit through the environment. Accumulating traces can accelerate convergence by magnifying frequent contributions, making them suitable for dynamic tasks requiring quick adaptation. On the other hand, replacing traces help mitigate overfitting to particular state transitions, ensuring a balanced and robust learning process that generalizes better across the environment.
The following Rust code implements a reinforcement learning algorithm, TD(λ) (Temporal Difference Learning with eligibility traces), to train an agent in the Mountain Car environment. The task involves navigating a mountain car environment, where the agent must learn to balance exploration and exploitation to reach a goal efficiently. The environment simulates a car stuck between two hills that must gain momentum to reach the goal on the right hilltop. The algorithm uses eligibility traces, which help balance short-term and long-term credit assignment by keeping track of state visitation history. The training uses two variations of trace updates: accumulate traces, where trace values increase incrementally, and replace traces, where traces are reset upon state revisits.
use std::collections::HashMap;
#[derive(Clone, Copy, Hash, PartialEq, Eq)]
struct QuantizedState(i32, i32);
struct MountainCar {
position_bounds: (f64, f64),
velocity_bounds: (f64, f64),
resolution: f64, // Determines quantization level
}
impl MountainCar {
fn quantize_state(&self, state: (f64, f64)) -> QuantizedState {
QuantizedState(
((state.0 - self.position_bounds.0) / self.resolution).round() as i32,
((state.1 - self.velocity_bounds.0) / self.resolution).round() as i32,
)
}
fn step(&self, state: (f64, f64), action: f64) -> ((f64, f64), f64) {
let next_velocity = (state.1 + action).clamp(self.velocity_bounds.0, self.velocity_bounds.1);
let next_position = (state.0 + next_velocity).clamp(self.position_bounds.0, self.position_bounds.1);
let reward = if next_position >= self.position_bounds.1 { 10.0 } else { -1.0 };
((next_position, next_velocity), reward)
}
}
fn accumulate_traces(
eligibility: &mut HashMap<QuantizedState, f64>,
state: QuantizedState,
gamma: f64,
lambda: f64,
) {
for trace in eligibility.values_mut() {
*trace *= gamma * lambda;
}
*eligibility.entry(state).or_insert(0.0) += 1.0;
}
fn replace_traces(
eligibility: &mut HashMap<QuantizedState, f64>,
state: QuantizedState,
gamma: f64,
lambda: f64,
) {
for (s, trace) in eligibility.iter_mut() {
if *s == state {
*trace = 1.0;
} else {
*trace *= gamma * lambda;
}
}
}
fn td_lambda(
env: &MountainCar,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
use_replace: bool,
) {
let mut eligibility_traces: HashMap<QuantizedState, f64> = HashMap::new();
let mut value_function: HashMap<QuantizedState, f64> = HashMap::new();
for _ in 0..episodes {
let mut state = (0.0, 0.0); // Start at bottom of the hill
while state.0 < env.position_bounds.1 {
let action = if rand::random::<f64>() < 0.1 { 1.0 } else { -1.0 }; // Random policy
let (next_state, reward) = env.step(state, action);
let quantized_state = env.quantize_state(state);
let quantized_next_state = env.quantize_state(next_state);
let td_error = reward
+ gamma * value_function.get(&quantized_next_state).unwrap_or(&0.0)
- value_function.get(&quantized_state).unwrap_or(&0.0);
if use_replace {
replace_traces(&mut eligibility_traces, quantized_state, gamma, lambda);
} else {
accumulate_traces(&mut eligibility_traces, quantized_state, gamma, lambda);
}
for (s, trace) in &eligibility_traces {
let value = value_function.entry(*s).or_insert(0.0);
*value += alpha * td_error * trace;
}
state = next_state;
}
}
}
fn main() {
let env = MountainCar {
position_bounds: (-1.2, 0.6),
velocity_bounds: (-0.07, 0.07),
resolution: 0.01, // Quantization resolution
};
let episodes = 500;
let alpha = 0.1;
let gamma = 0.9;
let lambda = 0.8;
println!("Training with accumulate traces...");
td_lambda(&env, episodes, alpha, gamma, lambda, false);
println!("Training with replace traces...");
td_lambda(&env, episodes, alpha, gamma, lambda, true);
}
The MountainCar struct defines the environment with bounds for the car's position and velocity. A step function simulates the dynamics of the environment, given a current state and action, returning the next state and a reward. To overcome the limitation of using floating-point values as keys in a HashMap, states are quantized into integers. The td_lambda function trains the agent over multiple episodes using a random policy. It calculates the TD error (difference between predicted and actual returns) and updates the value function using eligibility traces. Depending on the mode, traces are either accumulated or replaced to influence how states contribute to learning. The algorithm alternates between two trace update methods for comparison, iteratively improving the policy based on the car's ability to reach the goal efficiently.
The following updated version of the Mountain Car TD(λ) implementation builds on the initial code by introducing a comparative experiment to evaluate the performance of accumulate traces and replace traces strategies. The new code tracks the total reward achieved in each episode, computes average rewards over multiple episodes, and prints these metrics for both strategies. This addition allows for an empirical comparison of their convergence speed and stability, which was not included in the initial version.
use std::collections::HashMap;
#[derive(Clone, Copy, Hash, PartialEq, Eq)]
struct QuantizedState(i32, i32);
struct MountainCar {
position_bounds: (f64, f64),
velocity_bounds: (f64, f64),
resolution: f64, // Determines quantization level
}
impl MountainCar {
fn quantize_state(&self, state: (f64, f64)) -> QuantizedState {
QuantizedState(
((state.0 - self.position_bounds.0) / self.resolution).round() as i32,
((state.1 - self.velocity_bounds.0) / self.resolution).round() as i32,
)
}
fn step(&self, state: (f64, f64), action: f64) -> ((f64, f64), f64) {
let next_velocity = (state.1 + action).clamp(self.velocity_bounds.0, self.velocity_bounds.1);
let next_position = (state.0 + next_velocity).clamp(self.position_bounds.0, self.position_bounds.1);
let reward = if next_position >= self.position_bounds.1 { 10.0 } else { -1.0 };
((next_position, next_velocity), reward)
}
}
fn accumulate_traces(
eligibility: &mut HashMap<QuantizedState, f64>,
state: QuantizedState,
gamma: f64,
lambda: f64,
) {
for trace in eligibility.values_mut() {
*trace *= gamma * lambda;
}
*eligibility.entry(state).or_insert(0.0) += 1.0;
}
fn replace_traces(
eligibility: &mut HashMap<QuantizedState, f64>,
state: QuantizedState,
gamma: f64,
lambda: f64,
) {
for (s, trace) in eligibility.iter_mut() {
if *s == state {
*trace = 1.0;
} else {
*trace *= gamma * lambda;
}
}
}
fn td_lambda(
env: &MountainCar,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
use_replace: bool,
) -> Vec<f64> {
let mut eligibility_traces: HashMap<QuantizedState, f64> = HashMap::new();
let mut value_function: HashMap<QuantizedState, f64> = HashMap::new();
let mut rewards_per_episode = Vec::new();
for _ in 0..episodes {
let mut state = (0.0, 0.0); // Start at bottom of the hill
let mut total_reward = 0.0;
while state.0 < env.position_bounds.1 {
let action = if rand::random::<f64>() < 0.1 { 1.0 } else { -1.0 }; // Random policy
let (next_state, reward) = env.step(state, action);
let quantized_state = env.quantize_state(state);
let quantized_next_state = env.quantize_state(next_state);
let td_error = reward
+ gamma * value_function.get(&quantized_next_state).unwrap_or(&0.0)
- value_function.get(&quantized_state).unwrap_or(&0.0);
if use_replace {
replace_traces(&mut eligibility_traces, quantized_state, gamma, lambda);
} else {
accumulate_traces(&mut eligibility_traces, quantized_state, gamma, lambda);
}
for (s, trace) in &eligibility_traces {
let value = value_function.entry(*s).or_insert(0.0);
*value += alpha * td_error * trace;
}
state = next_state;
total_reward += reward;
}
rewards_per_episode.push(total_reward);
}
rewards_per_episode
}
fn main() {
let env = MountainCar {
position_bounds: (-1.2, 0.6),
velocity_bounds: (-0.07, 0.07),
resolution: 0.01, // Quantization resolution
};
for strategy in ["accumulate", "replace"] {
println!("Training with {} traces...", strategy);
let use_replace = strategy == "replace";
let rewards = td_lambda(&env, 500, 0.1, 0.9, 0.8, use_replace);
let average_reward: f64 = rewards.iter().copied().sum::<f64>() / rewards.len() as f64;
println!(
"Average reward over 500 episodes using {} traces: {:.2}",
strategy, average_reward
);
}
}
The program simulates training over 500 episodes for both accumulate and replace trace strategies, where the TD(λ) algorithm updates the value function and eligibility traces based on the agent's experience in the Mountain Car environment. The td_lambda function logs the cumulative reward for each episode, representing the agent's progress in learning to reach the goal. After training with each strategy, the program calculates the average reward to summarize overall performance and prints it for comparison. By running both strategies under the same conditions, it provides insights into their relative efficiency and effectiveness in policy improvement.
The experiment compares the speed and stability of convergence between the two strategies. Accumulate traces may show slower initial learning but smoother updates as traces build up over time. In contrast, replace traces can accelerate learning by prioritizing the most recent state, potentially leading to faster convergence but with the risk of instability due to abrupt trace updates. By observing the average rewards, we gain insights into which strategy is better suited for specific reinforcement learning problems, balancing speed and reliability. Additional analysis of the episode-wise rewards (e.g., plotting learning curves) can provide a deeper understanding of each strategy's behavior over time.
By implementing and experimenting with accumulate and replace eligibility traces, this section provides a comprehensive understanding of their trade-offs and applications in reinforcement learning. Readers are equipped with the theoretical insights and practical skills to choose and implement the best strategy for their tasks.
8.3. TD(λ) and the Generalization of Eligibility Traces
Reinforcement learning tasks often involve balancing short-term and long-term credit assignment when updating value functions. Traditional TD methods, such as TD(0), focus on immediate transitions and bootstrap from the next state’s value, offering computational efficiency and real-time adaptability. However, this single-step update limits their ability to capture relationships spanning multiple transitions. In contrast, n-step TD methods extend the credit assignment horizon by incorporating information from multiple successive steps before updating, bridging the gap between TD(0) and Monte Carlo methods. While effective, n-step TD methods require manually selecting a fixed step length nnn, which may not be optimal across different tasks or environments.
To overcome these limitations, eligibility traces were introduced as a flexible mechanism for propagating rewards to all contributing states in a dynamic and adaptive manner. Eligibility traces maintain a memory of visited states, decaying their influence over time based on recency. By integrating eligibility traces with TD learning, a more powerful framework emerged, enabling algorithms to blend updates from various time scales seamlessly. This integration set the stage for TD(λ), which generalizes the concepts of TD(0) and n-step TD by using eligibility traces to adjust the balance between short-term and long-term learning dynamically.
Temporal-Difference (TD) learning is one of the foundational pillars of reinforcement learning, enabling agents to estimate value functions by bootstrapping from intermediate predictions. TD(λ) extends TD(0) and n-step TD methods by introducing eligibility traces, which blend information from multiple steps in the learning process. This generalization offers a flexible framework, interpolating between short-term, bootstrapping-focused updates and long-term, trajectory-based methods.
The TD(λ) algorithm achieves this flexibility by using a decay parameter $\lambda$, which controls how eligibility traces fade over time. Mathematically, TD(λ) combines n-step returns weighted by $\lambda^{n-1}$, effectively summing over all possible n-step returns:
$$ G^\lambda_t = (1 - \lambda) \sum_{n=1}^\infty \lambda^{n-1} G_t^{(n)}, $$
where $G_t^{(n)}$ is the n-step return starting at time $t$. This formulation captures both short-term and long-term information, balancing bias and variance. The parameter $\lambda$ in TD(λ) plays a pivotal role in determining how the algorithm blends different time scales of learning:
When $\lambda = 0$, TD(λ) reduces to TD(0), which updates value estimates based solely on one-step transitions.
When $\lambda = 1$, TD(λ) approximates Monte Carlo methods, relying on the entire episode's return for updates.
Intermediate values of $\lambda$ allow TD(λ) to incorporate multi-step returns, providing a trade-off between the low bias of Monte Carlo methods and the low variance of TD(0). This balance makes TD(λ) a highly versatile algorithm for tasks where the dynamics or data availability may vary.
An analogy for understanding $\lambda$ is the adjustment of a thermostat. A low $\lambda$ corresponds to quick but narrow adjustments (short-term focus), while a high $\lambda$ allows for slower, broader changes (long-term focus).
TD(λ) is a cornerstone of policy evaluation, estimating the value function for a given policy by combining information from short- and long-term returns. It also plays a critical role in policy improvement, guiding the agent toward better actions by refining value estimates more effectively than TD(0) or Monte Carlo methods alone.
The eligibility trace mechanism enables TD(λ) to propagate rewards efficiently across multiple states, leading to faster convergence in policy evaluation. Moreover, its flexibility allows it to adapt to different task structures, making it suitable for both episodic and continuous tasks.
TD(λ) unifies concepts from various reinforcement learning algorithms:
It bridges the gap between TD(0), which focuses on immediate feedback, and Monte Carlo methods, which rely on complete trajectories.
It generalizes n-step TD methods by weighting returns from all possible n-step returns, eliminating the need to select a specific $n$.
The choice of $\lambda$ significantly impacts the learning process. Smaller $\lambda$ values emphasize recent experiences, leading to faster updates but higher variance. Larger $\lambda$ values incorporate longer-term information, reducing variance but potentially slowing convergence.
Higher $\lambda$ values lead to smoother updates due to the averaging effect of multi-step returns. However, this comes at the cost of slower adaptation to new information, as updates depend on longer sequences of transitions.
The following code implements a TD(λ) learning algorithm for a Maze environment and compares the performance of different λ values (0.0, 0.5, 1.0) to study their effects on learning. The Maze consists of a grid with a goal state, and the agent learns to navigate from the start to the goal using a reinforcement learning framework with eligibility traces. The program outputs episode rewards during execution and generates a learning curve plot to visualize how the agent's performance evolves over 500 episodes for each λ.
[dependencies]
itertools = "0.13.0"
plotters = "0.3.7"
use plotters::prelude::*;
use std::collections::HashMap;
use itertools::izip;
struct MazeEnv {
size: usize,
goal_state: (usize, usize),
}
impl MazeEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => ((state.0 + 1).min(self.size - 1), state.1), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
3 => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
_ => state, // Invalid action, stay in the same state
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 };
(next_state, reward)
}
}
const MAX_STEPS_PER_EPISODE: usize = 100;
fn td_lambda(
env: &MazeEnv,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> Vec<f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
let mut episode_rewards = Vec::new();
for episode in 0..episodes {
let mut state = (0, 0); // Start at top-left corner
let mut total_reward = 0.0;
let mut steps = 0;
while state != env.goal_state && steps < MAX_STEPS_PER_EPISODE {
let action = rand::random::<usize>() % 4; // Random action
let (next_state, reward) = env.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
// Update eligibility traces
for trace in eligibility_traces.values_mut() {
*trace *= gamma * lambda;
}
*eligibility_traces.entry(state).or_insert(0.0) += 1.0;
// Update value function
for (s, trace) in &eligibility_traces {
let value = value_function.entry(*s).or_insert(0.0);
*value += alpha * td_error * trace;
}
state = next_state;
total_reward += reward;
steps += 1;
}
if episode % 100 == 0 {
println!("Episode {}: Total Reward = {:.2}", episode, total_reward);
}
episode_rewards.push(total_reward);
eligibility_traces.clear();
}
episode_rewards
}
fn plot_rewards(rewards: &[Vec<f64>], lambdas: &[f64]) {
let root_area = BitMapBackend::new("td_lambda_rewards.png", (800, 600)).into_drawing_area();
root_area.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root_area)
.caption("TD(λ) Learning Curves", ("sans-serif", 30))
.margin(10)
.x_label_area_size(30)
.y_label_area_size(40)
.build_cartesian_2d(0..rewards[0].len(), -200.0..20.0)
.unwrap();
chart
.configure_mesh()
.x_desc("Episodes")
.y_desc("Total Reward")
.draw()
.unwrap();
let colors = [RED, BLUE, GREEN];
for (reward, &color, &lambda) in izip!(rewards, &colors, lambdas) {
chart
.draw_series(LineSeries::new(
reward.iter().enumerate().map(|(x, y)| (x, *y)),
&color,
))
.unwrap()
.label(format!("λ = {:.1}", lambda))
.legend(move |(x, y)| PathElement::new([(x, y)], &color));
}
chart
.configure_series_labels()
.background_style(&WHITE)
.border_style(&BLACK)
.draw()
.unwrap();
}
fn main() {
let env = MazeEnv {
size: 5,
goal_state: (4, 4),
};
let episodes = 500;
let alpha = 0.1;
let gamma = 0.9;
let lambdas = [0.0, 0.5, 1.0];
let mut rewards = Vec::new();
for &lambda in &lambdas {
println!("Training with λ = {}...", lambda);
let episode_rewards = td_lambda(&env, episodes, alpha, gamma, lambda);
rewards.push(episode_rewards);
}
println!("Plotting rewards...");
plot_rewards(&rewards, &lambdas);
println!("Learning curves saved as 'td_lambda_rewards.png'.");
}
The MazeEnv struct defines the environment, including movement logic and reward assignment. The td_lambda function trains the agent using the TD(λ) algorithm, updating value functions based on temporal difference errors and eligibility traces. A maximum step limit per episode prevents infinite loops, ensuring the agent progresses towards the goal. As the agent interacts with the environment, it accumulates total rewards for each episode. After training for all λ values, the program visualizes the episode rewards using the plotters crate, displaying the learning curves for comparison.
Figure 4: Plotters visualization of TD learning curve with different $\lambda$.
The visualization highlights the trade-offs between different λ values. With λ = 0.0, the agent updates its value function based on immediate rewards, leading to slower but steady learning. For λ = 0.5, learning accelerates as both short-term and long-term rewards are considered, striking a balance between speed and stability. When λ = 1.0, the agent relies entirely on future rewards, showing faster initial convergence but potentially higher variance. The learning curves provide a clear picture of convergence speed and stability, helping determine the most effective λ value for the given task.
This updated code extends the original implementation by adding a Monte Carlo method and comparing it against TD(0) and TD(λ) learning algorithms to evaluate their performance in navigating a Maze environment. The comparison highlights the strengths and weaknesses of each method in terms of convergence speed and stability. The code introduces a visualization to display learning curves, showcasing how total rewards evolve over 500 episodes for all three methods.
use plotters::prelude::*;
use std::collections::HashMap;
use itertools::izip;
use rand::Rng;
struct MazeEnv {
size: usize,
goal_state: (usize, usize),
}
impl MazeEnv {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => ((state.0 + 1).min(self.size - 1), state.1), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
3 => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
_ => state, // Invalid action, stay in the same state
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 };
(next_state, reward)
}
}
const MAX_STEPS_PER_EPISODE: usize = 100;
fn td_lambda(
env: &MazeEnv,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> Vec<f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
let mut episode_rewards = Vec::new();
for _ in 0..episodes {
let mut state = (0, 0);
let mut total_reward = 0.0;
let mut steps = 0;
while state != env.goal_state && steps < MAX_STEPS_PER_EPISODE {
let action = rand::thread_rng().gen_range(0..4);
let (next_state, reward) = env.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
for trace in eligibility_traces.values_mut() {
*trace *= gamma * lambda;
}
*eligibility_traces.entry(state).or_insert(0.0) += 1.0;
for (s, trace) in &eligibility_traces {
let value = value_function.entry(*s).or_insert(0.0);
*value += alpha * td_error * trace;
}
state = next_state;
total_reward += reward;
steps += 1;
}
eligibility_traces.clear();
episode_rewards.push(total_reward);
}
episode_rewards
}
fn monte_carlo(
env: &MazeEnv,
episodes: usize,
alpha: f64,
gamma: f64,
) -> Vec<f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut episode_rewards = Vec::new();
for _ in 0..episodes {
let mut state = (0, 0);
let mut total_reward = 0.0;
let mut trajectory = Vec::new();
while state != env.goal_state && trajectory.len() < MAX_STEPS_PER_EPISODE {
let action = rand::thread_rng().gen_range(0..4);
let (next_state, reward) = env.step(state, action);
trajectory.push((state, reward));
state = next_state;
total_reward += reward;
}
let mut g = 0.0;
for &(state, reward) in trajectory.iter().rev() {
g = reward + gamma * g;
let value = value_function.entry(state).or_insert(0.0);
*value += alpha * (g - *value);
}
episode_rewards.push(total_reward);
}
episode_rewards
}
fn plot_rewards(rewards: &[Vec<f64>], methods: &[&str]) {
let root_area = BitMapBackend::new("td_methods_comparison.png", (800, 600)).into_drawing_area();
root_area.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root_area)
.caption("Comparison of TD(0), TD(λ), and Monte Carlo", ("sans-serif", 30))
.margin(10)
.x_label_area_size(30)
.y_label_area_size(40)
.build_cartesian_2d(0..rewards[0].len(), -200.0..20.0)
.unwrap();
chart
.configure_mesh()
.x_desc("Episodes")
.y_desc("Total Reward")
.draw()
.unwrap();
let colors = [RED, BLUE, GREEN];
for (reward, &color, &method) in izip!(rewards, &colors, methods) {
chart
.draw_series(LineSeries::new(
reward.iter().enumerate().map(|(x, y)| (x, *y)),
&color,
))
.unwrap()
.label(method)
.legend(move |(x, y)| PathElement::new([(x, y), (x + 20, y)], color));
}
chart
.configure_series_labels()
.background_style(&WHITE)
.border_style(&BLACK)
.draw()
.unwrap();
}
fn main() {
let env = MazeEnv {
size: 5,
goal_state: (4, 4),
};
let episodes = 500;
let alpha = 0.1;
let gamma = 0.9;
println!("Training with TD(0)...");
let td0_rewards = td_lambda(&env, episodes, alpha, gamma, 0.0);
println!("Training with TD(λ)...");
let td_lambda_rewards = td_lambda(&env, episodes, alpha, gamma, 0.5);
println!("Training with Monte Carlo...");
let monte_carlo_rewards = monte_carlo(&env, episodes, alpha, gamma);
println!("Plotting rewards...");
plot_rewards(
&[td0_rewards, td_lambda_rewards, monte_carlo_rewards],
&["TD(0)", "TD(λ)", "Monte Carlo"],
);
println!("Learning curves saved as 'td_methods_comparison.png'.");
}
The Maze environment simulates a grid world where an agent learns to reach the goal state from the start through reinforcement learning. The TD(0) and TD(λ) methods update value functions incrementally during episodes using temporal difference errors and eligibility traces, respectively. The Monte Carlo method updates value functions at the end of episodes based on cumulative rewards for complete trajectories. The program tracks total rewards per episode for each method and generates learning curves using the plotters crate to visualize their performance over time.
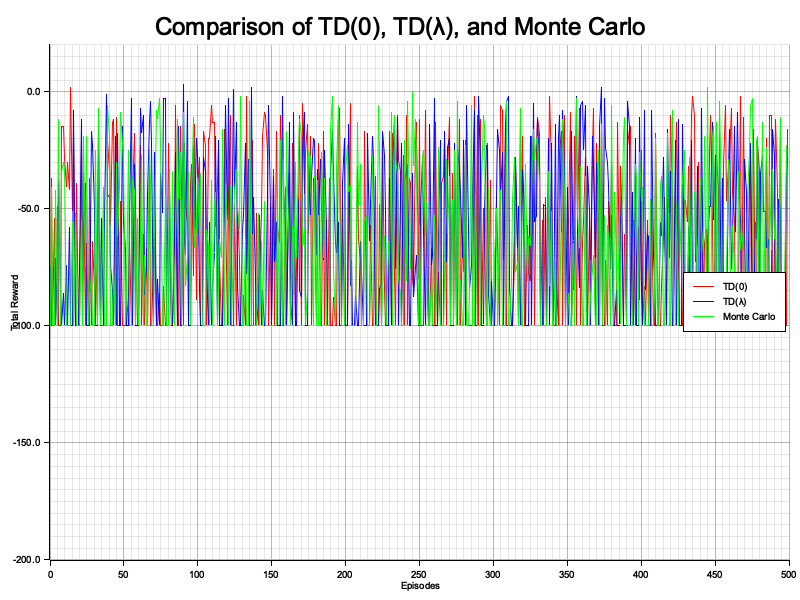
Figure 5: Plotters visualization of TD and Monte Carlo.
The visualization reveals the distinct characteristics of the three methods. TD(0) shows stable but slower convergence as it relies solely on immediate rewards. TD(λ) strikes a balance, offering faster learning by incorporating both short-term and long-term rewards, making it versatile for various tasks. Monte Carlo converges quickly in environments with dense rewards but may show instability in sparse reward settings due to delayed updates. The comparison underscores how TD(λ) combines the advantages of the other two methods, offering a practical balance between speed and stability in reinforcement learning tasks.
This section equips readers with a deep understanding of TD(λ) and its role in reinforcement learning. Through theoretical insights and practical Rust implementations, it highlights how eligibility traces enable efficient and flexible learning across diverse environments.
8.4. Forward and Backward View of Eligibility Traces
Eligibility traces are a cornerstone of reinforcement learning, providing a mechanism to bridge the gap between Temporal-Difference (TD) methods and Monte Carlo approaches. By maintaining a decaying memory of visited states, eligibility traces enable efficient credit assignment, ensuring that past states and actions receive appropriate updates based on their contribution to future rewards. This dynamic propagation of rewards across time is what makes eligibility traces indispensable for tasks involving delayed or sparse feedback.
To fully appreciate the utility of eligibility traces, it is essential to explore how they influence learning dynamics. This process can be understood through two complementary perspectives: the forward view and the backward view. Both perspectives offer distinct yet mathematically equivalent explanations of how eligibility traces function, each highlighting different aspects of their role in learning.
Figure 6: Different perspectives on eligibility traces in RL.
The forward view focuses on how returns from future steps are aggregated to update the value of the current state. This trajectory-based perspective emphasizes the long-term contribution of rewards, blending the concepts of n-step returns with a weighted sum that spans multiple time steps. It provides a theoretical framework that captures the essence of eligibility traces as a continuum between short-term and long-term learning, offering a precise mathematical basis for understanding their integration into reinforcement learning algorithms.
The backward view, in contrast, emphasizes the propagation of rewards backward in time to update past states. This perspective highlights the operational mechanics of eligibility traces, showcasing how they decay over time and how updates are recursively distributed to states in proportion to their recency and frequency of visitation. The backward view aligns closely with practical implementations, as it leverages the recursive structure of Temporal-Difference (TD) methods to achieve computational efficiency.
Despite their differences, the forward and backward views are fundamentally equivalent and serve as two sides of the same coin. Together, they provide a comprehensive understanding of how eligibility traces facilitate credit assignment, enhance learning efficiency, and bridge the strengths of TD and Monte Carlo methods. Understanding both perspectives equips reinforcement learning practitioners with the theoretical and practical tools to implement eligibility traces effectively in diverse environments.
The forward view of eligibility traces centers on the idea of n-step returns. The return for a given state $s_t$ is expressed as a weighted sum of returns from different time scales:
$$G_t^\lambda = (1 - \lambda) \sum_{n=1}^\infty \lambda^{n-1} G_t^{(n)},$$
where:
$G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n})$ is the n-step return,
$\lambda$ controls the weighting of returns from different time scales.
This formulation shows how eligibility traces integrate information from both short-term (TD-like) and long-term (Monte Carlo-like) perspectives. The forward view highlights how TD(λ) generalizes these methods, providing a seamless blend of bias and variance.
The backward view of eligibility traces takes a different approach, focusing on how updates to value functions are distributed backward across states. This perspective is built on the idea of temporal credit assignment, where eligibility traces act as a memory mechanism for recently visited states:
$$ E_t(s) = \gamma \lambda E_{t-1}(s) + \mathbf{1}(S_t = s), $$
where $\mathbf{1}(S_t = s)$ is an indicator function.
The backward view directly connects eligibility traces to updates in the value function:
$$ \Delta V(s) = \alpha \delta_t E_t(s), $$
where $\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$ is the TD error. This formulation emphasizes the immediate impact of rewards on states that influenced the outcome, making it computationally efficient and intuitive.
While conceptually distinct, the forward and backward views are mathematically equivalent. The forward view provides a theoretical understanding of how multi-step returns contribute to value updates, while the backward view offers a practical mechanism for implementing these updates efficiently. This equivalence ensures that both perspectives lead to the same learning outcomes, allowing researchers and practitioners to choose the approach that best suits their needs.
This code implements both the forward view and backward view of TD(λ) in a random walk environment to compare their theoretical foundations and practical applications. The forward view explicitly calculates n-step returns for each state and combines them using λ-weighted averaging, while the backward view leverages eligibility traces to propagate updates across states efficiently. The program trains the agent in the random walk environment using both methods, computes the resulting value functions, and visualizes their comparison.
use plotters::prelude::*;
use std::collections::HashMap;
struct RandomWalkEnv {
size: usize,
start_state: usize,
goal_state: usize,
}
impl RandomWalkEnv {
fn step(&self, state: usize, action: i32) -> (usize, f64, bool) {
let next_state = if action == -1 && state > 0 {
state - 1
} else if action == 1 && state < self.size - 1 {
state + 1
} else {
state
};
let reward = if next_state == self.goal_state { 1.0 } else { 0.0 };
let done = next_state == self.goal_state || next_state == 0;
(next_state, reward, done)
}
}
fn forward_td_lambda(
env: &RandomWalkEnv,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> HashMap<usize, f64> {
let mut value_function: HashMap<usize, f64> = (0..env.size).map(|s| (s, 0.0)).collect();
for _ in 0..episodes {
let mut state = env.start_state;
let mut trajectory = Vec::new();
while state != 0 && state != env.goal_state {
let action = if rand::random::<bool>() { 1 } else { -1 };
let (next_state, reward, done) = env.step(state, action);
trajectory.push((state, reward));
state = next_state;
if done {
trajectory.push((state, 0.0)); // Terminal state
break;
}
}
for t in 0..trajectory.len() {
let (s, _) = trajectory[t];
let mut g = 0.0;
let mut weight = 1.0;
for n in 0..trajectory.len() - t {
let (sn, r) = trajectory[t + n];
g += r * weight;
weight *= gamma;
if n > 0 {
g += lambda * value_function.get(&sn).unwrap_or(&0.0);
}
}
let value = value_function.entry(s).or_insert(0.0);
*value += alpha * (g - *value);
}
}
value_function
}
fn backward_td_lambda(
env: &RandomWalkEnv,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
) -> HashMap<usize, f64> {
let mut value_function: HashMap<usize, f64> = (0..env.size).map(|s| (s, 0.0)).collect();
for _ in 0..episodes {
let mut state = env.start_state;
let mut eligibility_traces: HashMap<usize, f64> = HashMap::new();
while state != 0 && state != env.goal_state {
let action = if rand::random::<bool>() { 1 } else { -1 };
let (next_state, reward, done) = env.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
for trace in eligibility_traces.values_mut() {
*trace *= gamma * lambda;
}
*eligibility_traces.entry(state).or_insert(0.0) += 1.0;
for (s, trace) in &eligibility_traces {
let value = value_function.entry(*s).or_insert(0.0);
*value += alpha * td_error * trace;
}
state = next_state;
if done {
break;
}
}
}
value_function
}
fn plot_value_functions(
forward_values: &HashMap<usize, f64>,
backward_values: &HashMap<usize, f64>,
) {
let root_area = BitMapBackend::new("value_function_comparison_updated.png", (800, 600)).into_drawing_area();
root_area.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root_area)
.caption("Updated Value Function Comparison: Forward vs Backward TD(λ)", ("sans-serif", 20))
.margin(20)
.x_label_area_size(30)
.y_label_area_size(40)
.build_cartesian_2d(0..(forward_values.len() - 1), 0.0..1.0)
.unwrap();
chart
.configure_mesh()
.x_desc("State")
.y_desc("Value")
.draw()
.unwrap();
let forward_series = forward_values
.iter()
.map(|(&state, &value)| (state, value))
.collect::<Vec<_>>();
let backward_series = backward_values
.iter()
.map(|(&state, &value)| (state, value))
.collect::<Vec<_>>();
chart
.draw_series(LineSeries::new(forward_series, &BLUE))
.unwrap()
.label("Forward TD(λ)")
.legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &BLUE));
chart
.draw_series(LineSeries::new(backward_series, &RED))
.unwrap()
.label("Backward TD(λ)")
.legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &RED));
chart
.configure_series_labels()
.background_style(&WHITE)
.border_style(&BLACK)
.draw()
.unwrap();
}
fn main() {
let env = RandomWalkEnv {
size: 7,
start_state: 3,
goal_state: 6,
};
let episodes = 10000; // Increased episodes for better convergence
let alpha = 0.05; // Adjusted learning rate for stability
let gamma = 1.0; // No discounting as it's episodic
let lambda = 0.8;
println!("Training with Forward TD(λ)...");
let forward_values = forward_td_lambda(&env, episodes, alpha, gamma, lambda);
println!("Value Function (Forward TD(λ)): {:?}", forward_values);
println!("Training with Backward TD(λ)...");
let backward_values = backward_td_lambda(&env, episodes, alpha, gamma, lambda);
println!("Value Function (Backward TD(λ)): {:?}", backward_values);
println!("Plotting value functions...");
plot_value_functions(&forward_values, &backward_values);
println!("Updated value functions saved as 'value_function_comparison_updated.png'.");
}
The random walk environment is a linear grid where the agent starts at a central state and aims to reach a terminal state (goal or boundary). The forward view iterates over full trajectories to compute n-step returns for each state, requiring storage and processing of the entire trajectory. In contrast, the backward view avoids explicit computation of n-step returns by updating value functions incrementally using eligibility traces, which decay over time unless reinforced. Both methods are trained over multiple episodes, and their value functions are plotted for comparison using the plotters crate.
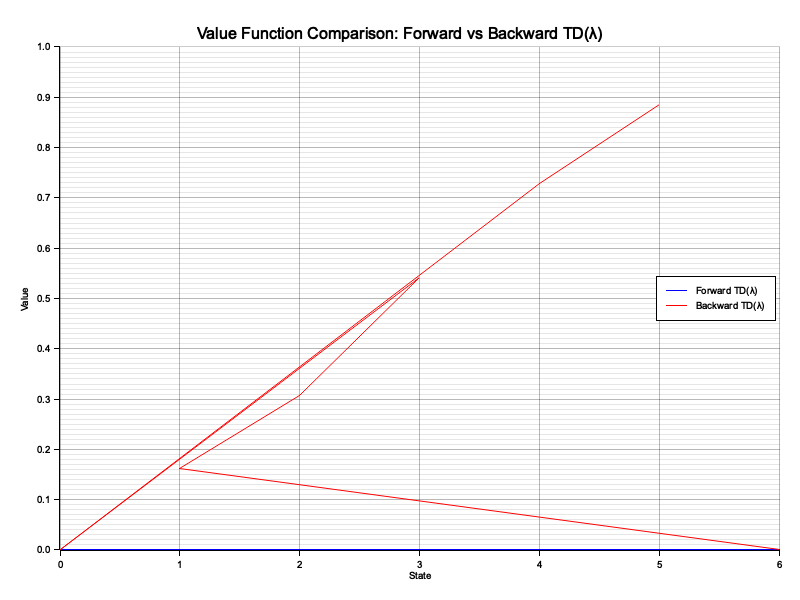
Figure 7: Plotters visualization of value functions of forward and backward TD($\lambda$).
The visualization highlights the equivalence of the forward and backward views, with both converging to similar value functions after sufficient training. The forward view is computationally intensive due to trajectory storage and processing, making it less practical for large-scale environments. Conversely, the backward view achieves equivalent results more efficiently by propagating updates dynamically using eligibility traces. The plot demonstrates that while both approaches align theoretically, the backward view is better suited for real-world applications requiring scalability and efficiency.
This section combines rigorous mathematical explanations with practical Rust implementations to illuminate the forward and backward views of eligibility traces. By exploring these complementary perspectives, readers gain a deep understanding of the mechanics and flexibility of TD(λ) in reinforcement learning.
8.5. Challenges and Best Practices in Using Eligibility Traces
Eligibility traces are a powerful mechanism in reinforcement learning, enabling efficient propagation of rewards across multiple states and blending the strengths of Temporal-Difference (TD) and Monte Carlo methods. However, their versatility comes with inherent challenges that must be addressed to ensure stable and effective learning. These challenges center on the decay parameter $\lambda$, trace management, and overall learning stability.
The decay parameter $\lambda$ is a pivotal element of eligibility traces, controlling how quickly traces fade over time. It effectively balances the influence of short-term and long-term rewards, shaping the agent’s ability to assign credit across multiple time steps. A small $\lambda$ biases the algorithm toward short-term dependencies, closely resembling TD(0), which focuses on immediate feedback and single-step updates. While this reduces variance, it may fail to capture relationships between states that span multiple transitions. Conversely, a large $\lambda$ approaches the behavior of Monte Carlo methods, emphasizing long-term rewards and multi-step dependencies. However, this can amplify noise in the environment, increase variance in value estimates, and slow down learning. Striking the right balance with $\lambda$ is task-dependent, often requiring empirical tuning or adaptive strategies to optimize performance.
Figure 8: Key challenges in eligibility traces of RL.
In environments where states are frequently revisited, managing trace decay becomes a critical consideration. Eligibility traces accumulate credit over time, with states visited multiple times retaining a higher influence on updates. While this can enhance learning in certain scenarios, it also introduces the risk of over-crediting, where specific states disproportionately dominate updates. This imbalance can destabilize the learning process, especially when combined with large discount factors $\gamma$ or inappropriate $\lambda$ settings. Effective trace management requires carefully tuning both $\gamma$ and $\lambda$, ensuring that the cumulative effect of eligibility traces does not lead to runaway credit assignment. Techniques such as normalizing traces or capping their maximum values can mitigate this risk and maintain stability.
Eligibility traces introduce dependencies between states over multiple time steps, which can amplify errors if the learning process is not carefully managed. This interdependence increases the complexity of credit assignment, making the learning process more sensitive to inaccuracies in value estimates or noisy feedback from the environment. To stabilize learning, it is essential to employ strategies such as regularization to prevent overfitting and exploration techniques to ensure diverse state visitation. Additionally, techniques like experience replay and target networks, commonly used in deep reinforcement learning, can help decouple dependencies and mitigate the cascading effect of errors. Robust optimization methods, including adaptive learning rates and gradient clipping, are also critical for managing the dynamic interactions between eligibility traces and the reinforcement learning update rules.
While eligibility traces significantly enhance the flexibility and efficiency of reinforcement learning algorithms, their use requires careful consideration of several challenges. The decay parameter λ\\lambdaλ, trace management, and learning stability are interconnected factors that influence the success of eligibility trace-based methods. Addressing these challenges involves a combination of theoretical understanding, empirical tuning, and the use of stabilizing techniques, ensuring that eligibility traces achieve their potential in diverse and complex learning environments. By navigating these challenges effectively, eligibility traces can serve as a robust tool for bridging short-term and long-term learning in reinforcement learning.
The parameter $\lambda$ determines how eligibility traces blend information from different time scales. Mathematically, $\lambda$ influences the decay of the eligibility trace $E_t(s)$ as follows:
$$ E_t(s) = \gamma \lambda E_{t-1}(s) + \mathbf{1}(S_t = s), $$
where $\mathbf{1}(S_t = s)$ indicates whether state $s$ was visited at time $t$.
When $\lambda$ is close to 0, TD(λ) behaves like TD(0), focusing on immediate rewards with low variance but higher bias.
When $\lambda$ approaches 1, TD(λ) approximates Monte Carlo methods, incorporating longer-term returns with low bias but higher variance.
Choosing the right $\lambda$ requires understanding the task and environment. For tasks with frequent state revisits or strong long-term dependencies, a higher $\lambda$ may be beneficial. Conversely, in noisy or rapidly changing environments, a lower $\lambda$ can stabilize learning.
To prevent the accumulation of excessive credit, regularization techniques such as weight decay or trace normalization can be applied. For example, normalizing eligibility traces ensures that their total contribution remains bounded:
$$ E_t(s) \leftarrow \frac{E_t(s)}{\sum_{s'} E_t(s')}. $$
Exploration strategies like epsilon-greedy policies interact with eligibility traces by influencing the frequency of state visits. Sufficient exploration ensures that eligibility traces are distributed across the state space, preventing overfitting to frequently visited states. Careful tuning of $\gamma$, $\lambda$, and the learning rate $\alpha$ is essential for stable updates. Adaptive methods that adjust these parameters based on the learning progress can further enhance convergence.
The following Rust program implements the TD(λ) algorithm with eligibility traces in a GridWorld environment, utilizing an epsilon-greedy policy for exploration. The GridWorld is a 5x5 grid where the agent starts at the top-left corner and aims to reach a goal state at the bottom-right corner, receiving a positive reward for reaching the goal and a penalty otherwise. The code demonstrates training with different epsilon values (0.1, 0.3, 0.5) to explore how varying degrees of exploration affect the agent's value function.
use std::collections::HashMap;
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => ((state.0 + 1).min(self.size - 1), state.1), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 };
(next_state, reward)
}
}
fn normalize_traces(traces: &mut HashMap<(usize, usize), f64>) {
let total: f64 = traces.values().sum();
if total > 0.0 {
for trace in traces.values_mut() {
*trace /= total;
}
}
}
fn td_lambda(
env: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
epsilon: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
for _ in 0..episodes {
let mut state = (0, 0); // Start at top-left corner
while state != env.goal_state {
// Epsilon-greedy exploration
let action = if rand::random::<f64>() < epsilon {
rand::random::<usize>() % 4
} else {
(0..4)
.max_by(|&a, &b| {
let value_a = value_function
.get(&env.step(state, a).0)
.unwrap_or(&0.0);
let value_b = value_function
.get(&env.step(state, b).0)
.unwrap_or(&0.0);
value_a
.partial_cmp(value_b)
.unwrap_or(std::cmp::Ordering::Equal)
})
.unwrap_or(0)
};
let (next_state, reward) = env.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
// Update eligibility traces
for trace in eligibility_traces.values_mut() {
*trace *= gamma * lambda;
}
*eligibility_traces.entry(state).or_insert(0.0) += 1.0;
// Normalize eligibility traces
normalize_traces(&mut eligibility_traces);
// Update value function
for (s, trace) in &eligibility_traces {
let value = value_function.entry(*s).or_insert(0.0);
*value += alpha * td_error * trace;
}
state = next_state;
}
// Decay traces after each episode
eligibility_traces.clear();
}
value_function
}
fn main() {
let env = GridWorld {
size: 5,
goal_state: (4, 4),
};
let episodes = 500;
let alpha = 0.1;
let gamma = 0.9;
let lambda = 0.8;
for epsilon in [0.1, 0.3, 0.5] {
println!("Training with epsilon = {}...", epsilon);
let value_function = td_lambda(&env, episodes, alpha, gamma, lambda, epsilon);
println!("Value Function: {:?}", value_function);
}
}
The environment allows the agent to move up, down, left, or right, constrained by the grid's boundaries. Using the TD(λ) algorithm, the agent learns a value function for each state by propagating rewards across states using eligibility traces. The epsilon-greedy policy balances exploration and exploitation: the agent either explores by taking random actions with probability epsilon or exploits the current value function to select the best action. Eligibility traces, normalized at each step, decay over time unless reinforced by state revisits, enabling the backward propagation of TD errors. The value function updates iteratively over 500 episodes, and the resulting value function is printed for each epsilon setting.
This next experiment evaluates different exploration strategies using the epsilon-greedy method in a 5x5 GridWorld environment. The agent starts at the top-left corner and aims to reach the goal state at the bottom-right corner, learning state values through the TD(λ) algorithm. By varying the epsilon values (0.1, 0.3, 0.5), the experiment analyzes how exploration levels influence the stability and efficiency of learning, leveraging eligibility traces for backward updates and plotting the resulting value functions for each strategy.
use plotters::prelude::*;
use std::collections::HashMap;
struct GridWorld {
size: usize,
goal_state: (usize, usize),
}
impl GridWorld {
fn step(&self, state: (usize, usize), action: usize) -> ((usize, usize), f64) {
let next_state = match action {
0 => (state.0.saturating_sub(1), state.1), // Move up
1 => ((state.0 + 1).min(self.size - 1), state.1), // Move down
2 => (state.0, state.1.saturating_sub(1)), // Move left
_ => (state.0, (state.1 + 1).min(self.size - 1)), // Move right
};
let reward = if next_state == self.goal_state { 10.0 } else { -1.0 };
(next_state, reward)
}
}
fn normalize_traces(traces: &mut HashMap<(usize, usize), f64>) {
let total: f64 = traces.values().sum();
if total > 0.0 {
for trace in traces.values_mut() {
*trace /= total;
}
}
}
fn td_lambda(
env: &GridWorld,
episodes: usize,
alpha: f64,
gamma: f64,
lambda: f64,
epsilon: f64,
) -> HashMap<(usize, usize), f64> {
let mut value_function: HashMap<(usize, usize), f64> = HashMap::new();
let mut eligibility_traces: HashMap<(usize, usize), f64> = HashMap::new();
for _ in 0..episodes {
let mut state = (0, 0); // Start at top-left corner
while state != env.goal_state {
// Epsilon-greedy exploration
let action = if rand::random::<f64>() < epsilon {
rand::random::<usize>() % 4
} else {
(0..4)
.max_by(|&a, &b| {
let value_a = value_function
.get(&env.step(state, a).0)
.unwrap_or(&0.0);
let value_b = value_function
.get(&env.step(state, b).0)
.unwrap_or(&0.0);
value_a
.partial_cmp(value_b)
.unwrap_or(std::cmp::Ordering::Equal)
})
.unwrap_or(0)
};
let (next_state, reward) = env.step(state, action);
let td_error = reward
+ gamma * value_function.get(&next_state).unwrap_or(&0.0)
- value_function.get(&state).unwrap_or(&0.0);
// Update eligibility traces
for trace in eligibility_traces.values_mut() {
*trace *= gamma * lambda;
}
*eligibility_traces.entry(state).or_insert(0.0) += 1.0;
// Normalize eligibility traces
normalize_traces(&mut eligibility_traces);
// Update value function
for (s, trace) in &eligibility_traces {
let value = value_function.entry(*s).or_insert(0.0);
*value += alpha * td_error * trace;
}
state = next_state;
}
// Decay traces after each episode
eligibility_traces.clear();
}
value_function
}
fn plot_value_functions(
value_functions: Vec<HashMap<(usize, usize), f64>>,
epsilons: &[f64],
env: &GridWorld,
) {
let root_area = BitMapBackend::new("exploration_strategies.png", (800, 600)).into_drawing_area();
root_area.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root_area)
.caption("Exploration Strategies: Epsilon-Greedy Comparison", ("sans-serif", 20))
.margin(20)
.x_label_area_size(40)
.y_label_area_size(50)
.build_cartesian_2d(0..env.size, -1.0..10.0)
.unwrap();
chart
.configure_mesh()
.x_desc("State Index (Linearized)")
.y_desc("Value")
.draw()
.unwrap();
let colors = [BLUE, RED, GREEN];
for (i, value_function) in value_functions.iter().enumerate() {
let series = value_function
.iter()
.map(|(&(x, y), &value)| (x * env.size + y, value))
.collect::<Vec<_>>();
chart
.draw_series(LineSeries::new(series, &colors[i]))
.unwrap()
.label(format!("Epsilon = {}", epsilons[i]))
.legend(move |(x, y)| PathElement::new([(x, y), (x + 20, y)], &colors[i]));
}
chart
.configure_series_labels()
.background_style(&WHITE)
.border_style(&BLACK)
.draw()
.unwrap();
}
fn main() {
let env = GridWorld {
size: 5,
goal_state: (4, 4),
};
let episodes = 7000;
let alpha = 0.1;
let gamma = 0.9;
let lambda = 0.8;
let epsilons = [0.1, 0.3, 0.5];
let mut value_functions = Vec::new();
for &epsilon in &epsilons {
println!("Training with epsilon = {}...", epsilon);
let value_function = td_lambda(&env, episodes, alpha, gamma, lambda, epsilon);
value_functions.push(value_function);
}
println!("Plotting exploration strategies...");
plot_value_functions(value_functions, &epsilons, &env);
println!("Plot saved as 'exploration_strategies.png'.");
}
The GridWorld environment provides transitions and rewards for the agent's actions. The agent follows an epsilon-greedy policy, balancing exploration (random actions with probability epsilon) and exploitation (choosing the action with the highest estimated value). The TD(λ) algorithm updates the value function incrementally based on temporal difference errors and eligibility traces, which decay over time unless reinforced. After training for 7000 episodes, the code stores value functions for different epsilon values and visualizes them using the plotters crate. Each state is linearized for clear comparison on a single plot.
Figure 9: Plotters visualization of exploration strategies experiment on epsilon-greedy algorithm.
The plot reveals how varying epsilon values affect the learning process. Low epsilon (0.1) prioritizes exploitation, resulting in faster convergence but potentially suboptimal value estimation due to insufficient exploration. Medium epsilon (0.3) strikes a balance, producing smoother and more robust value estimates across the grid. High epsilon (0.5) encourages exploration, which leads to broader learning but slower convergence and less stable value estimation. This experiment demonstrates that balanced exploration strategies, such as medium epsilon values, often result in the most stable and efficient learning.
This section equips readers with a comprehensive understanding of the challenges and best practices in using eligibility traces. By combining theoretical insights with practical Rust implementations, it provides a robust framework for designing stable and efficient reinforcement learning algorithms.
8.6. Conclusion
Chapter 8 emphasizes the importance of eligibility traces as a unifying framework in reinforcement learning, offering flexibility and efficiency in learning from both immediate and delayed rewards. By mastering the implementation of eligibility traces using Rust, readers will gain the ability to tackle complex reinforcement learning tasks with greater precision and stability, ensuring that their models learn efficiently from experience.
8.6.1. Further Learning with GenAI
By engaging with these prompts, you will gain a comprehensive understanding of how eligibility traces bridge the gap between Temporal-Difference (TD) learning and Monte Carlo methods, and how to effectively implement and optimize them in various reinforcement learning tasks using Rust.
Explain the fundamental principles of eligibility traces in reinforcement learning. How do eligibility traces unify TD learning and Monte Carlo methods? Implement a basic eligibility trace algorithm in Rust and discuss its significance.
Discuss the concept of the decay parameter (λ) in eligibility traces. How does λ control the influence of past experiences on current learning? Implement a TD(λ) algorithm in Rust and experiment with different λ values to observe their impact.
Explore the difference between accumulating and replacing eligibility traces. How do these two strategies affect the accumulation of eligibility in reinforcement learning? Implement both strategies in Rust and compare their performance on a reinforcement learning task.
Analyze the trade-offs involved in choosing between accumulate and replace eligibility traces. In what scenarios would one be preferred over the other? Experiment with these strategies in Rust to understand their implications on convergence and stability.
Discuss the role of eligibility traces in balancing bias and variance in reinforcement learning. How does the choice of λ influence this balance? Implement a TD(λ) algorithm in Rust and analyze the effects of different λ values on bias and variance.
Examine the connection between TD(λ) and other reinforcement learning methods, such as TD(0) and Monte Carlo. How does varying λ allow TD(λ) to interpolate between these methods? Implement a Rust-based simulation to observe this interpolation in action.
Explore the forward view of eligibility traces. How does this perspective help in understanding n-step returns and their relation to TD(λ)? Implement the forward view in Rust and analyze its impact on the learning process.
Discuss the backward view of eligibility traces. How does this perspective provide a more intuitive understanding of how rewards are propagated backward through time? Implement the backward view in Rust and visualize the propagation of rewards in a reinforcement learning task.
Analyze the equivalence between the forward and backward views of eligibility traces. How are these two perspectives mathematically related, and why is this equivalence important? Implement both views in Rust and compare their outcomes.
Explore the challenges of managing the decay of eligibility traces. What techniques can be used to prevent the accumulation of too much credit, and how do these techniques impact learning? Implement decay management strategies in Rust and evaluate their effectiveness.
Discuss the impact of exploration strategies, such as epsilon-greedy policies, on the performance of eligibility traces. How do these strategies interact with eligibility traces and influence learning outcomes? Implement and experiment with different exploration strategies in Rust.
Examine the role of eligibility traces in policy evaluation and improvement. How do traces contribute to more efficient and stable learning in reinforcement learning tasks? Implement a TD(λ) algorithm in Rust and test its effectiveness on policy improvement.
Analyze the trade-offs between using eligibility traces with high vs. low λ values. How do these choices affect learning speed, stability, and convergence? Experiment with different λ values in Rust and observe their impact on a reinforcement learning task.
Discuss the challenges of implementing eligibility traces in environments with continuous state spaces. What adaptations are necessary to handle continuous environments? Implement a TD(λ) algorithm in Rust for a continuous state space and explore these challenges.
Explore the importance of regularization when using eligibility traces. How does regularization help maintain stability and prevent the over-accumulation of credit? Implement regularization techniques in Rust and analyze their effects on the learning process.
Examine the application of eligibility traces in complex reinforcement learning tasks, such as robotic control or game AI. How do traces enhance learning efficiency in these tasks? Implement a Rust-based eligibility trace algorithm for a complex task and evaluate its performance.
Discuss the relationship between eligibility traces and function approximation. How do eligibility traces interact with function approximators, such as neural networks? Implement an eligibility trace algorithm in Rust with a function approximator and analyze the outcomes.
Analyze the convergence properties of TD(λ) with eligibility traces. Under what conditions is convergence guaranteed, and how does the choice of λ affect this? Implement a TD(λ) algorithm in Rust and test its convergence behavior in different scenarios.
Explore the use of eligibility traces in off-policy learning methods. How do traces impact the stability and accuracy of off-policy methods like Q-learning? Implement an off-policy algorithm with eligibility traces in Rust and compare it to an on-policy approach.
Discuss the ethical considerations of applying eligibility traces in real-world reinforcement learning scenarios, such as autonomous vehicles or healthcare systems. What risks are associated with these applications, and how can they be mitigated? Implement a TD(λ) algorithm in Rust for a real-world-inspired scenario and analyze the ethical implications.
By diving into these comprehensive questions and engaging with hands-on implementations in Rust, you will gain a deep understanding of how eligibility traces can be effectively applied to a wide range of reinforcement learning tasks.
8.6.2. Hands On Practices
These exercises encourage hands-on experimentation and thorough engagement with the concepts, allowing readers to apply their knowledge practically.
Exercise 8.1: Implementing and Analyzing Accumulate vs. Replace Eligibility Traces
Task:
Implement both accumulate and replace eligibility trace strategies in Rust for a reinforcement learning task, such as navigating a grid world or balancing a cart-pole.
Challenge:
Compare the performance of the accumulate and replace strategies in terms of convergence speed, stability, and accuracy. Experiment with different values of λ and analyze how each strategy impacts the overall learning process.
Discuss which strategy is more effective in different scenarios and why.
Exercise 8.2: Exploring the Forward and Backward Views of Eligibility Traces
Task:
Implement both the forward and backward views of eligibility traces in Rust for a simple reinforcement learning task, such as a random walk.
Challenge:
Compare the forward and backward views by visualizing how eligibility traces propagate through the states over time. Analyze the similarities and differences between these two perspectives and how they affect the learning dynamics.
Provide insights into when one view might be preferred over the other in practical applications.
Exercise 8.3: Experimenting with TD(λ) and Function Approximation
Task:
Implement a TD(λ) algorithm with a function approximator, such as a neural network, in Rust for a continuous state-space task, like controlling a robotic arm or navigating a continuous grid world.
Challenge:
Explore how different values of λ impact the interaction between eligibility traces and the function approximator. Analyze how the choice of λ affects the learning efficiency, accuracy, and convergence stability in continuous environments.
Discuss the challenges encountered when integrating eligibility traces with function approximation and how they can be mitigated.
Exercise 8.4: Managing Decay in Eligibility Traces
Task:
Implement a decay management strategy for eligibility traces in Rust to prevent the over-accumulation of credit in a reinforcement learning task, such as mountain car.
Challenge:
Experiment with different decay rates and observe their effects on learning stability and convergence speed. Analyze the trade-offs between aggressive and conservative decay strategies in terms of learning efficiency and policy performance.
Provide recommendations for selecting appropriate decay rates based on the characteristics of the task and environment.
Exercise 8.5: Applying Eligibility Traces to Off-Policy Learning
Task:
Implement an off-policy learning algorithm, such as Q-Learning, with eligibility traces in Rust, and apply it to a complex task, such as a game AI or autonomous vehicle simulation.
Challenge:
Analyze how the integration of eligibility traces affects the stability and accuracy of the off-policy learning process. Compare the performance of the off-policy method with eligibility traces to an on-policy approach, such as SARSA, under similar conditions.
Discuss the challenges of using eligibility traces in off-policy learning and propose strategies to mitigate potential issues.
By engaging with these tasks in Rust, you will gain a deeper understanding of how eligibility traces can be used to enhance the learning process in various reinforcement learning scenarios.
Comments