Chapter 11
Introduction to Multi-Agent Systems
"Alone we can do so little; together we can do so much." — Herbert A. Simon
Chapter 11 introduces the fascinating world of Multi-Agent Systems (MAS) within reinforcement learning, providing a comprehensive exploration of their theoretical foundations, conceptual advancements, and practical implementations. It begins by formalizing the mathematical underpinnings of MAS, such as Decentralized Partially Observable Markov Decision Processes (Dec-POMDPs) and joint policy spaces, and moves to a detailed taxonomy of system types, including autonomous, semi-autonomous, and human-in-the-loop MAS. Key sections delve into the dynamics of communication and coordination, the integration of game theory for strategic interactions, and advanced reinforcement learning algorithms tailored for multi-agent contexts. Practical applications span cutting-edge domains like swarm robotics, decentralized finance, and human-AI collaboration, with Rust-based implementations and frameworks providing hands-on insights. The chapter concludes by addressing the challenges and future directions of MAS, focusing on scalability, ethical considerations, and emerging paradigms such as lifelong learning and integration with quantum computing.
11.1. Overview of Multi-Agents Systems
The evolution of Multi-Agent Systems (MAS) reflects a continuous journey of innovation driven by the need to address increasingly complex, decentralized, and dynamic problems across various domains. MAS traces its roots to the conceptual foundations of distributed computing and artificial intelligence in the 1970s and 1980s. Researchers began exploring the idea of autonomous agents—self-contained entities capable of independent decision-making—motivated by the limitations of centralized systems in handling distributed tasks. Early MAS frameworks focused on distributed problem-solving systems, where agents acted as local solvers collaborating within a network to achieve global objectives. These systems were pivotal in advancing research in fields like networked systems, database management, and fault-tolerant computing.
The 1980s also saw the emergence of knowledge-based systems, where agents were designed to exhibit reasoning capabilities based on predefined rules or logic. This marked a shift towards creating agents with higher autonomy, capable of proactive behavior rather than mere reactive responses. During this period, the concept of intentional agents—entities with goals, beliefs, and intentions—laid the groundwork for cognitive MAS, inspiring early applications in scheduling, manufacturing, and supply chain management.
Figure 1: The historical evolution of Multi-Agent Systems in RL.
By the 1990s, MAS research had matured, incorporating robust theoretical frameworks to formalize agent interactions. A significant milestone was the integration of game theory into MAS, enabling the modeling of strategic decision-making among agents with competing or cooperative goals. Concepts like Nash Equilibrium, Pareto Efficiency, and the Minimax Theorem became foundational tools for analyzing agent strategies in scenarios such as auctions, negotiations, and resource allocation. Concurrently, formal models such as Markov Games and Partially Observable Markov Decision Processes (POMDPs) provided rigorous mathematical structures for capturing the dynamics of multi-agent interactions in stochastic environments. This period also witnessed the rise of MAS applications in robotics, where agents were employed for distributed tasks like multi-robot exploration, and in logistics, where MAS optimized warehouse operations and supply chains.
The 2000s marked a transformative phase for MAS, driven by the rapid advancements in machine learning and computational power. Reinforcement Learning (RL) emerged as a natural complement to MAS, enabling agents to learn optimal policies through trial and error in dynamic and uncertain environments. This integration allowed MAS to move beyond static rule-based behaviors, empowering agents to adapt and optimize their strategies in real-time. The development of Decentralized POMDPs (Dec-POMDPs) further expanded the theoretical scope of MAS, providing a formal framework for decentralized decision-making under partial observability—a key requirement for real-world systems like sensor networks and autonomous vehicles.
Simultaneously, the growth of computational resources facilitated the application of MAS to more complex and large-scale problems. Researchers began exploring hierarchical MAS, where agents operate at different levels of abstraction, and meta-learning MAS, where agents learn to adapt across tasks. Real-world applications flourished during this era, with MAS revolutionizing fields like finance, where multi-agent simulations modeled market dynamics, and energy systems, where MAS optimized grid operations and load balancing.
Modern MAS research builds on these foundations, focusing on scalability, adaptability, and the integration of deep learning. The advent of deep reinforcement learning (DRL) has significantly enhanced the capabilities of MAS, enabling agents to process high-dimensional inputs such as images and unstructured data. DRL techniques, combined with advanced MAS architectures, have been pivotal in tackling real-world challenges like autonomous driving, where fleets of vehicles coordinate to optimize traffic flow, and swarm robotics, where large groups of robots exhibit emergent behaviors for tasks like disaster recovery or environmental monitoring.
Moreover, the increasing complexity of modern systems has led to a renewed focus on ethics and fairness in MAS, addressing concerns like bias, transparency, and accountability in multi-agent decision-making. Applications like decentralized finance (DeFi), healthcare optimization, and smart cities exemplify the potential of MAS to transform industries while highlighting the need for responsible deployment.
In summary, the journey of MAS reflects a profound interplay between theoretical innovation and practical application. From its origins in distributed computing to its modern-day integration with deep learning and reinforcement learning, MAS continues to push the boundaries of what autonomous and collaborative systems can achieve, offering transformative solutions to some of the world’s most complex problems.
Mathematically, an MAS comprises multiple agents $\{a_1, a_2, \ldots, a_n\}$, an environment $\mathcal{E}$, a state space $\mathcal{S}$, actions $\mathcal{A}$, policies $\pi$, and utilities $U$. Each agent $a_i$ selects actions based on its policy $\pi_i$ to maximize cumulative rewards $U_i$, which are functions of the environment's state transitions and rewards. The interactions can be modeled as Markov Games or Dec-POMDPs. For example, in a Dec-POMDP:
$$ \text{Dec-POMDP} = \langle \mathcal{A}, \mathcal{S}, \mathcal{A}, \mathcal{O}, \mathcal{P}, \mathcal{R}, \gamma \rangle, $$
where $\mathcal{O}$ is the observation space, and each agent $a_i$ observes $o_i \in \mathcal{O}_i$. Agents aim to maximize a joint utility $U$:
$$ U = \mathbb{E} \left[ \sum_{t=0}^\infty \gamma^t R(s_t, \mathbf{a}_t) \right]. $$
This mathematical foundation facilitates the design of cooperative, competitive, or hybrid MAS frameworks.
Below is a complete Rust implementation of a basic MAS framework that integrates agent interaction, environment simulation, and visualization. This implementation represents a custom multi-agent reinforcement learning environment where autonomous agents interact with a shared state space. The core concept involves agents with individual policies that collectively influence and adapt to a dynamic environment. Unlike traditional RL models, this implementation focuses on a simplified, deterministic interaction where agents generate actions based on their learned policy weights, and the environment evolves through a combination of agent actions, current state, and controlled randomness. The model simulates how different agents might collaboratively or competitively modify a multi-dimensional state vector, demonstrating emergent behaviors through their interactions.
[dependencies]
plotters = "0.3.7"
rand = "0.8.5"
use plotters::prelude::*;
use rand::Rng;
// Define the Environment struct
struct Environment {
state: Vec<f64>,
agents: Vec<Agent>,
}
impl Environment {
fn new(num_agents: usize, state_dim: usize) -> Self {
let mut rng = rand::thread_rng();
let agents = (0..num_agents).map(|_| Agent::new(state_dim)).collect();
Self {
state: (0..state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect(),
agents,
}
}
fn step(&mut self, actions: Vec<f64>) -> Vec<f64> {
// More complex state update with some noise and decay
let mut rng = rand::thread_rng();
self.state.iter_mut().zip(actions.iter()).enumerate().for_each(|(_i, (s, a))| {
// Weighted update with current state, action, and some randomness
*s = 0.7 * *s + 0.2 * *a + 0.1 * rng.gen_range(-0.5..0.5);
// Optional: Clamp the state to prevent extreme values
*s = s.clamp(-10.0, 10.0);
});
self.state.clone()
}
}
// Define the Agent struct
struct Agent {
policy: Vec<f64>, // Simplified policy representation
}
impl Agent {
fn new(state_dim: usize) -> Self {
let mut rng = rand::thread_rng();
Self {
policy: (0..state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect(),
}
}
fn act(&self, state: &[f64]) -> f64 {
// More dynamic action selection
state.iter().zip(self.policy.iter())
.map(|(s, p)| s * p)
.sum::<f64>()
.clamp(-5.0, 5.0)
}
}
// Function for visualizing agent dynamics
fn plot_dynamics(states: Vec<Vec<f64>>) -> Result<(), Box<dyn std::error::Error>> {
let root = BitMapBackend::new("agent_dynamics.png", (800, 600)).into_drawing_area();
root.fill(&WHITE)?;
let max_t = states.len();
let max_state = states.iter().flat_map(|s| s.iter().cloned()).fold(f64::NEG_INFINITY, f64::max);
let min_state = states.iter().flat_map(|s| s.iter().cloned()).fold(f64::INFINITY, f64::min);
let mut chart = ChartBuilder::on(&root)
.caption("Agent Dynamics", ("sans-serif", 50))
.margin(20)
.x_label_area_size(30)
.y_label_area_size(40)
.build_cartesian_2d(0..max_t, min_state..max_state)?;
chart.configure_mesh().draw()?;
// Transpose the states for plotting
let transposed_states: Vec<Vec<f64>> = (0..states[0].len())
.map(|dim| states.iter().map(|state| state[dim]).collect())
.collect();
for (dim_id, series) in transposed_states.iter().enumerate() {
chart
.draw_series(LineSeries::new(
series.iter().enumerate().map(|(t, &v)| (t, v)),
&Palette99::pick(dim_id),
))?
.label(format!("Dimension {}", dim_id))
.legend(move |(x, y)| {
PathElement::new(vec![(x, y), (x + 20, y)], &Palette99::pick(dim_id))
});
}
chart.configure_series_labels().draw()?;
Ok(())
}
// Main function to simulate and visualize MAS
fn main() -> Result<(), Box<dyn std::error::Error>> {
let num_agents = 3;
let state_dim = 5;
let mut env = Environment::new(num_agents, state_dim);
let mut states_over_time = Vec::new();
// Initial state
states_over_time.push(env.state.clone());
println!("Initial state: {:?}", env.state);
for _ in 0..100 {
let actions: Vec<f64> = env.agents.iter().map(|agent| agent.act(&env.state)).collect();
let new_state = env.step(actions);
states_over_time.push(new_state.clone());
println!("New state: {:?}", new_state);
}
// Visualize agent dynamics
plot_dynamics(states_over_time)?;
Ok(())
}
The code structures the multi-agent system around two primary structs: Environment and Agent. The Environment manages the global state and contains multiple agents, with each simulation step involving agents generating actions based on their current policy by analyzing the environment's state. The step() method updates the state through a weighted mechanism that preserves previous state information, incorporates agent actions, and introduces slight randomness to prevent deterministic behavior. Agents have randomly initialized policies that act as their decision-making mechanism, converting state information into actions. The simulation runs for a predefined number of steps, collecting state snapshots at each iteration, and ultimately visualizes the state dynamics using Plotters to generate a PNG image that shows how different state dimensions evolve over time, providing insights into the agent-environment interactions.
The evolution of the environment’s state is recorded over multiple time steps, capturing how agent actions collectively influence the system. After each time step, the new state of the environment is printed, providing immediate feedback about the dynamics of the simulation. This iterative interaction between agents and the environment demonstrates the fundamental principle of MAS: the behavior of individual agents cumulatively impacts the global system.
Finally, the visualization of agent dynamics is achieved using the plotters crate. After the simulation completes, the collected states are processed to generate a time-series plot. This plot provides a graphical representation of how the environment’s state evolves under the influence of agent actions, with each state dimension corresponding to a line in the chart. By visualizing these dynamics, users can gain insights into the behavior of the agents and the emergent patterns in the system.
Figure 2: Plotters visualization of agent dynamics.
Overall, this code encapsulates the essential elements of MAS, combining theoretical principles with practical implementation. It showcases how Rust’s performance and concurrency features make it an excellent choice for simulating and analyzing complex multi-agent systems. The modularity of the framework allows for easy extension, enabling researchers and developers to experiment with advanced agent behaviors, reward structures, and learning algorithms.
This section traced the historical evolution of MAS, from its early roots in distributed computing to its integration with reinforcement learning. The formalization of MAS dynamics provides a robust foundation for building multi-agent frameworks. Through a practical Rust implementation, we demonstrated how agents and environments interact, showcasing the power of modern tools like Tokio and Plotters for scalable, visualizable MAS experimentation. This foundation sets the stage for more complex MAS scenarios involving learning, coordination, and strategic decision-making.
11.2. Taxonomy of Multi-Agent Systems (MAS)
The taxonomy of Multi-Agent Systems (MAS) categorizes the various architectures, paradigms, and interaction mechanisms employed to model multi-agent behavior. This taxonomy provides a framework for understanding how agents operate and collaborate in decentralized, dynamic environments. Modern MAS are classified into Autonomous MAS, Semi-Autonomous MAS, and Human-in-the-Loop MAS, each with distinct operational principles and use cases. Additionally, graph-theoretic models, hierarchical structures, and emerging paradigms like swarm intelligence and stigmergy enhance the versatility and scalability of MAS. This section delves into these classifications and demonstrates their implementation through a unified Rust-based framework.
Autonomous MAS consist of agents operating independently with minimal or no external intervention. Examples include robotic swarms for exploration or autonomous vehicles in traffic systems. These systems are designed for scalability, adaptability, and efficiency in fully automated environments.
Semi-Autonomous MAS integrate limited human oversight or control, striking a balance between autonomy and guidance. Drone fleets monitored by ground operators exemplify such systems, where high-level instructions guide decentralized agent behaviors.
Human-in-the-Loop MAS place humans at the core of decision-making processes, relying on human expertise for complex or sensitive tasks. Applications range from healthcare systems where doctors guide AI diagnostics to financial systems where human traders influence algorithmic strategies.
Each category aligns with specific operational goals and constraints, offering flexibility for real-world deployments.
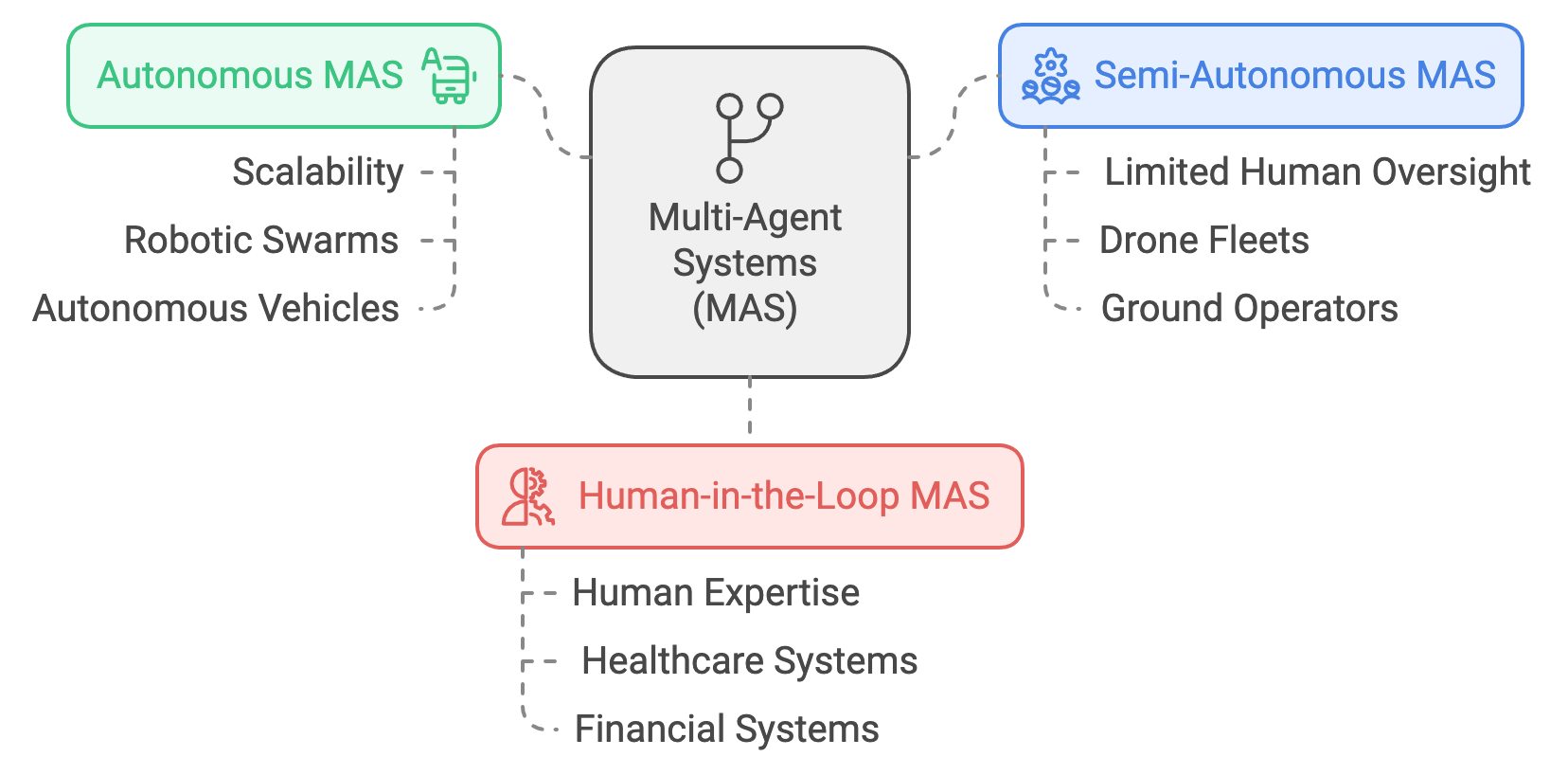
Figure 3: Scopes of MAS - Autonomous, Semi-Autonomous and Human-in-the-Loop.
Graph theory provides a powerful abstraction for modeling interactions within MAS. Agents are represented as nodes $V$, and their interactions as edges $E$ in a weighted graph $G = (V, E, W)$, where weights $W$ quantify interaction intensity, resource exchange, or trust levels. For instance, in a logistics MAS, nodes represent warehouses, edges represent shipping routes, and weights represent shipping costs or times.
Hierarchical MAS further structure agent interactions into tiers. A leader-follower hierarchy decomposes tasks into high-level coordination by leader agents and execution by worker agents. Formally, this hierarchy is defined as:
$$ H = \{L, W\}, \quad L \cap W = \emptyset, $$
where $L$ denotes leaders and $W$ denotes workers. Such hierarchies improve scalability and decision-making by delegating roles based on agent capabilities.
Modern MAS research incorporates paradigms like stigmergy, reputation systems, and market-driven coordination.
Stigmergy, inspired by social insects, enables indirect communication via environmental markers. In swarm robotics, agents modify the environment (e.g., depositing markers) to guide others, reducing the need for direct communication.
Reputation systems evaluate trust and reliability among agents based on past interactions, promoting cooperation in competitive environments like e-commerce platforms or decentralized networks.
Market-driven coordination models agents as economic entities optimizing resource allocation through auction mechanisms or pricing strategies, enabling efficient management of shared resources.
Swarm intelligence and self-organizing systems are further examples of MAS paradigms that achieve complex global behaviors through simple local rules. Applications include disaster recovery operations, autonomous fleet navigation, and distributed sensor networks.
The following Rust implementation integrates graph-theoretic modeling, hierarchical roles, and visualizations in a unified file. This code simulates agent interactions and visualizes their dynamics.
use std::collections::HashMap;
use plotters::prelude::*;
/// Define an Agent with roles and attributes
#[derive(Clone)]
struct Agent {
id: usize,
_role: Role, // Prefix with underscore to silence unused variable warning
}
#[derive(Clone)]
enum Role {
Leader,
Worker,
}
impl Agent {
fn new(id: usize) -> Self {
let role = if id % 2 == 0 { Role::Leader } else { Role::Worker };
Self {
id,
_role: role // Use the underscore prefix
}
}
}
/// Define a graph-based MAS structure
struct MASGraph {
agents: Vec<Agent>,
edges: HashMap<(usize, usize), f64>, // Weighted edges
}
impl MASGraph {
fn new(num_agents: usize) -> Self {
let agents = (0..num_agents).map(|id| Agent::new(id)).collect();
Self {
agents,
edges: HashMap::new(),
}
}
fn add_edge(&mut self, from: usize, to: usize, weight: f64) {
self.edges.insert((from, to), weight);
}
fn simulate_interactions(&self) -> HashMap<usize, f64> {
let mut outcomes = HashMap::new();
for agent in &self.agents {
let interactions: f64 = self
.edges
.iter()
.filter(|((from, _), _)| *from == agent.id)
.map(|(_, &weight)| weight)
.sum();
outcomes.insert(agent.id, interactions);
}
outcomes
}
}
/// Plotting utility to visualize agent interactions
fn plot_interactions(outcomes: &HashMap<usize, f64>) -> Result<(), Box<dyn std::error::Error>> {
// Increased image size for better visibility
let root = BitMapBackend::new("agent_interactions.png", (1200, 800)).into_drawing_area();
root.fill(&WHITE)?;
let max_value = outcomes.values().cloned().fold(0.0, f64::max);
let mut chart = ChartBuilder::on(&root)
.caption("Agent Interactions Network", ("Arial", 40).into_font())
.margin(20)
.x_label_area_size(60)
.y_label_area_size(80)
.build_cartesian_2d(0..outcomes.len(), 0.0..max_value * 1.2)?;
// Enhanced mesh with more detailed grid
chart.configure_mesh()
.x_desc("Agent ID")
.y_desc("Interaction Intensity")
.bold_line_style(&WHITE)
.light_line_style(&BLUE.mix(0.1))
.draw()?;
// Create a color gradient for more visual interest
let color_gradient = |x| {
let intensity = (x as f64 / outcomes.len() as f64) * 255.0;
RGBColor(
(intensity * 0.7) as u8,
(255.0 - intensity * 0.5) as u8,
(255.0 - intensity) as u8
)
};
// Draw bars with color gradient and hover-like information
chart.draw_series(
outcomes.iter().enumerate().map(|(i, (_, &value))| {
Rectangle::new(
[(i, 0.0), (i + 1, value)],
color_gradient(i).filled(),
)
})
)?;
// Add value labels on top of each bar
chart.draw_series(
outcomes.iter().enumerate().map(|(i, (_, &value))| {
Text::new(
format!("{:.2}", value),
(i + 1, value),
("Arial", 15).into_font()
)
})
)?;
root.present()?;
Ok(())
}
fn main() {
// Initialize the MAS graph with more complex interactions
let mut graph = MASGraph::new(8);
graph.add_edge(0, 1, 1.5);
graph.add_edge(0, 2, 2.0);
graph.add_edge(1, 3, 1.8);
graph.add_edge(2, 4, 1.3);
graph.add_edge(3, 5, 0.9);
graph.add_edge(4, 6, 1.1);
graph.add_edge(5, 7, 0.7);
graph.add_edge(6, 7, 1.6);
// Simulate interactions
let outcomes = graph.simulate_interactions();
println!("Agent Interaction Outcomes: {:?}", outcomes);
// Plot interactions
plot_interactions(&outcomes).expect("Failed to plot interactions");
}
This implementation begins with the MASGraph struct, which models agents and their relationships as a weighted graph. Each agent is represented by an Agent struct, which assigns roles (Leader or Worker) based on agent IDs. Interactions between agents are modeled as directed edges with weights that represent the intensity or frequency of interactions. The simulate_interactions method calculates the cumulative interaction weights for each agent by summing the weights of outgoing edges. This represents the influence or activity level of each agent within the system. The resulting values are stored in a hash map for further analysis. The visualization uses the plotters crate to generate a bar chart, where each bar corresponds to an agent’s cumulative interaction value. This graphical representation helps identify patterns in agent behaviors and their relationships.
Figure 4: Plotters visualization of agent interaction values.
This taxonomy highlights the diverse structures and paradigms in MAS, bridging theoretical foundations with practical applications. The Rust-based framework demonstrates how to model and visualize MAS interactions, offering a scalable and extensible foundation for exploring advanced MAS concepts in real-world scenarios. By combining hierarchical roles, graph-theoretic models, and emerging paradigms, this taxonomy equips developers with tools to design robust and adaptive multi-agent systems.
11.3. Communication and Coordination in MAS
Communication and coordination are cornerstones of Multi-Agent Systems (MAS), enabling agents to collaborate, share critical information, and align their strategies to achieve shared objectives. These capabilities become particularly essential in complex, dynamic environments where individual decision-making is insufficient to address systemic challenges. Effective communication ensures that agents can adapt their behavior in real-time, mitigating uncertainties and fostering robust cooperation. This section explores the mathematical underpinnings of communication in MAS, conceptual insights into emergent behaviors and fault-tolerant coordination, and practical implementations in Rust.
Communication in Multi-Agent Systems (MAS) is fundamentally an information exchange process where agents share states, intentions, or policies to minimize uncertainty and align actions across the system. This process ensures that the agents act cohesively, particularly in dynamic or uncertain environments. The mathematical modeling of such communication often leverages principles from information theory and graph-based models, which formalize the exchange of information and the topology of agent interactions.
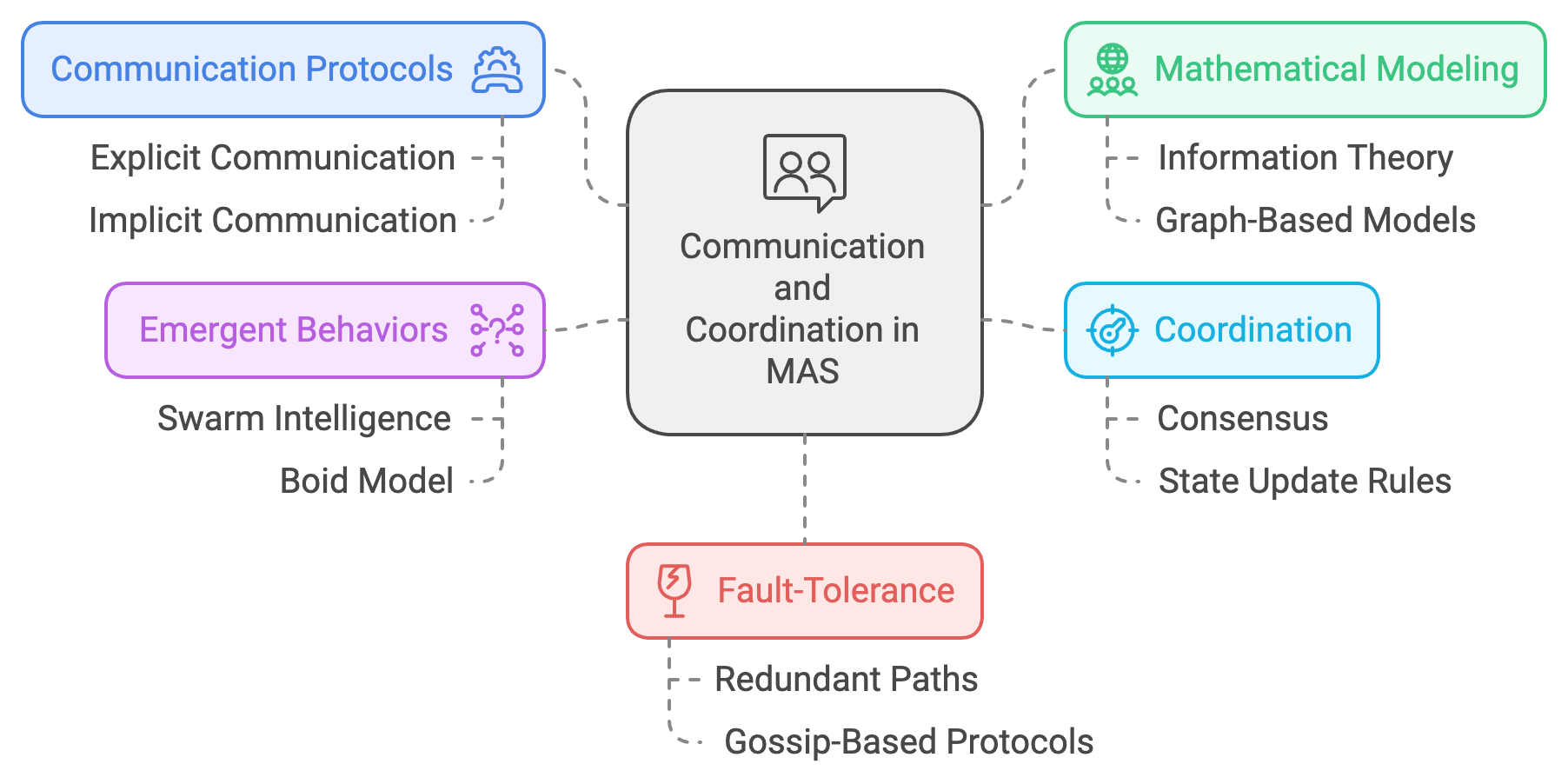
Figure 5: Theoretical scopes of communication and coordination in MAS.
Communication in MAS is classified into explicit and implicit protocols. In explicit communication, agents exchange structured messages directly. Let $\mathcal{C}_i$ be the communication protocol for agent $i$, defined as:
$$ \mathcal{C}_i: \mathcal{S} \times \mathcal{A} \to \mathcal{M}, $$
where $\mathcal{S}$ is the state space, $\mathcal{A}$ is the action space, and $\mathcal{M}$ is the message space. Implicit communication relies on shared states or environmental changes as indirect signals.
Coordination is modeled as a consensus problem, where agents converge to a shared value or strategy over time. If $x_i(t)$ represents the state of agent $i$ at time $t$, consensus ensures:
$$ \lim_{t \to \infty} |x_i(t) - x_j(t)| = 0 \quad \forall i, j. $$
From an information theory perspective, the amount of information exchanged between agents can be quantified using Shannon entropy. For a communication channel between agent $i$ and agent $j$, the mutual information $I(X; Y)$ measures the reduction in uncertainty about $Y$ (the state of agent $j$) given $X$ (the state of agent $i$). Mathematically, this is expressed as $I(X; Y) = H(Y) - H(Y \mid X)$, where $H(Y)$ is the entropy of $Y$ and $H(Y \mid X)$ is the conditional entropy. This metric ensures that the communication between agents is meaningful and not redundant, optimizing the bandwidth and computational resources. By focusing on the most informative aspects of the state, agents can prioritize critical data for exchange, enhancing efficiency.
Graph-based models provide another robust framework for modeling communication in MAS. Here, communication is represented as a graph $G = (V, E)$, where $V$ is the set of agents, and $E$ represents the communication links between them. Each edge $e_{ij}$ between agents $i$ and $j$ is weighted by $w_{ij}$, reflecting the cost or reliability of the communication link. The graph’s adjacency matrix AAA encodes this topology, with $A_{ij} = w_{ij}$ indicating the quality of the link between agents $i$ and $j$. Using this graph representation, agents can perform message-passing algorithms, a foundational technique in multi-agent coordination. For instance, in consensus algorithms, agents iteratively update their state xix_ixi based on the states of their neighbors. The state update rule is given by $x_i^{(t+1)} = x_i^{(t)} + \alpha \sum_{j \in N(i)} w_{ij} (x_j^{(t)} - x_i^{(t)})$, where $\alpha$ is the step size, and $N(i)$ denotes the neighbors of agent $i$. This iterative process allows agents to converge on a common state, enabling coordinated decision-making.
Effective communication in MAS also fosters emergent behaviors, where the interactions of individual agents give rise to collective intelligence. Swarm intelligence is a prime example, where groups of agents like drones or robots exhibit behaviors such as flocking, foraging, or formation control. These behaviors emerge from simple local communication rules, as demonstrated by the Boid model, which uses alignment, separation, and cohesion rules to achieve complex group dynamics.
Another key advantage of robust communication in MAS is enabling decentralized decision-making. Through effective communication, agents can align their actions without relying on a central authority, increasing system resilience against single points of failure. This is particularly valuable in environments with high latency or partial observability, such as autonomous driving systems or disaster response scenarios.
Finally, communication also underpins fault-tolerance in MAS, ensuring that the system remains operational even when individual agents or communication links fail. Fault-tolerant systems often rely on redundant communication paths and adaptive protocols to maintain functionality. For example, gossip-based protocols enable robust message propagation across unreliable networks, ensuring that critical information reaches all agents despite potential disruptions. These attributes make communication not only a fundamental aspect of MAS but also a critical enabler of their robustness and scalability.
Machine learning models enhance communication by interpreting unstructured or dynamic messages. For instance, reinforcement learning can optimize message exchange protocols, while natural language processing (NLP) models can decode human instructions in Human-in-the-Loop MAS.
Below is a complete Rust program integrating decentralized communication, dynamic coordination through shared states, and implicit communication using shared rewards. The code demonstrates a multi-agent system using Rust's asynchronous programming capabilities with Tokio. The model represents a distributed coordination scenario where agents can communicate through message passing and share a common state. Each agent is modeled with a unique identifier, a channel for sending messages, and access to a shared state protected by a mutex. The system includes an environment that manages rewards, allowing for implicit communication and coordination between agents. The agents can send messages to each other, update a shared state, and interact with an environment that tracks their collective performance. This approach mimics simple multi-agent reinforcement learning scenarios, where agents can communicate, modify a shared state, and receive rewards based on their actions, all achieved through Rust's powerful concurrency primitives and asynchronous programming model.
[dependencies]
tokio = { version = "1.41", features = ["full"] }
use tokio::sync::mpsc;
use tokio::task;
use std::sync::Arc;
use tokio::sync::Mutex;
/// Define an Agent struct
struct Agent {
id: usize,
tx: mpsc::Sender<String>,
shared_state: Arc<Mutex<Vec<f64>>>,
}
impl Agent {
fn new(
id: usize,
tx: mpsc::Sender<String>,
shared_state: Arc<Mutex<Vec<f64>>>,
) -> Self {
Self { id, tx, shared_state }
}
/// Asynchronous method for sending messages
async fn send_message(&self, message: &str) -> Result<(), mpsc::error::SendError<String>> {
self.tx.send(format!("Agent {}: {}", self.id, message)).await
}
/// Update shared state asynchronously
async fn update_state(&self, value: f64) {
let mut state = self.shared_state.lock().await;
state[self.id] += value;
println!("Agent {} updated shared state: {:?}", self.id, *state);
}
}
/// Define the Environment struct for implicit communication
struct Environment {
rewards: Vec<f64>,
}
impl Environment {
fn new(num_agents: usize) -> Self {
Self {
rewards: vec![0.0; num_agents],
}
}
fn update_rewards(&mut self, agent_id: usize, contribution: f64) {
self.rewards[agent_id] += contribution;
println!("Environment updated rewards: {:?}", self.rewards);
}
}
/// Main function demonstrating communication and coordination
#[tokio::main]
async fn main() -> Result<(), Box<dyn std::error::Error>> {
// Shared state for dynamic coordination
let shared_state = Arc::new(Mutex::new(vec![0.0; 3]));
// Communication channels for agents
let (tx1, mut rx1) = mpsc::channel(10);
let (tx2, mut rx2) = mpsc::channel(10);
let (tx3, mut rx3) = mpsc::channel(10);
// Initialize agents
let agent1 = Agent::new(0, tx2.clone(), Arc::clone(&shared_state));
let agent2 = Agent::new(1, tx3.clone(), Arc::clone(&shared_state));
let agent3 = Agent::new(2, tx1.clone(), Arc::clone(&shared_state));
// Initialize environment for implicit communication
let mut environment = Environment::new(3);
// Spawn tasks for agents
let task1 = task::spawn(async move {
if let Err(e) = agent1.send_message("Hello, Agent 3!").await {
eprintln!("Agent 1 send error: {}", e);
}
agent1.update_state(1.5).await;
});
let task2 = task::spawn(async move {
if let Err(e) = agent2.send_message("Acknowledged, Agent 1.").await {
eprintln!("Agent 2 send error: {}", e);
}
agent2.update_state(2.0).await;
});
let task3 = task::spawn(async move {
if let Err(e) = agent3.send_message("Ready for coordination.").await {
eprintln!("Agent 3 send error: {}", e);
}
agent3.update_state(3.0).await;
});
// Simulate implicit communication through shared rewards
environment.update_rewards(0, 5.0);
environment.update_rewards(1, 3.5);
environment.update_rewards(2, 4.0);
// Optional: Handle received messages (if needed)
tokio::spawn(async move {
while let Some(msg) = rx1.recv().await {
println!("Received on rx1: {}", msg);
}
});
tokio::spawn(async move {
while let Some(msg) = rx2.recv().await {
println!("Received on rx2: {}", msg);
}
});
tokio::spawn(async move {
while let Some(msg) = rx3.recv().await {
println!("Received on rx3: {}", msg);
}
});
// Await all tasks
task1.await?;
task2.await?;
task3.await?;
Ok(())
}
The provided Rust code demonstrates a comprehensive framework for communication and coordination in Multi-Agent Systems (MAS) using asynchronous programming with tokio. Agents communicate explicitly through asynchronous message-passing channels (mpsc), enabling decentralized exchange of information. Each agent can also update a shared global state, modeled as a thread-safe vector protected by a Mutex, allowing for dynamic coordination through shared variables. Implicit communication is simulated via an environment that maintains and updates a shared reward vector, representing indirect signaling among agents. The use of tokio ensures concurrency and scalability, allowing agents to perform messaging, state updates, and reward adjustments simultaneously without blocking. This integration of explicit and implicit communication, shared-state coordination, and fault-tolerant design showcases a robust implementation of MAS principles suitable for distributed and dynamic environments.
Communication and coordination are vital components of Multi-Agent Systems, enabling agents to work together effectively in distributed and dynamic environments. This section covered the mathematical foundations of communication protocols, consensus problems, and influence graphs, alongside conceptual insights into emergent behaviors and fault tolerance. The unified Rust implementation demonstrated decentralized messaging, shared-state coordination, and implicit communication using rewards. By leveraging Rust's concurrency capabilities, the framework offers a robust, scalable, and fault-tolerant approach to building complex MAS.
11.4. Game Theory and Strategic Interactions in MAS
Game theory, the study of strategic interactions among decision-making agents, has its origins in economics and mathematics, where it was initially developed to analyze competitive and cooperative behavior in systems involving rational entities. The field was formally established in the early 20th century with foundational contributions by mathematicians like John von Neumann and economists like Oskar Morgenstern. Their seminal work, Theory of Games and Economic Behavior (1944), introduced key concepts such as zero-sum games and equilibrium strategies, laying the groundwork for modern game theory.
Figure 6: MAS is Multi-Agent Problem Solving using Game Theory and RL Methods.
The concept of equilibrium, particularly Nash equilibrium introduced by John Nash in the 1950s, revolutionized the understanding of multi-agent interactions. Nash equilibrium provided a rigorous way to predict outcomes in games where each agent acts to maximize their utility, considering the actions of others. This idea of mutual best responses has since become a cornerstone of game theory, with applications spanning economics, biology, political science, and computer science.
In the context of Multi-Agent Systems (MAS), game theory provides a framework for modeling the interactions of autonomous agents pursuing individual or collective goals. As MAS gained prominence in the mid-20th century, game theory began to intersect with artificial intelligence (AI), particularly in areas like distributed systems, robotics, and strategic planning. The advent of reinforcement learning (RL) in the 1980s and 1990s, driven by pioneers such as Richard Sutton and Andrew Barto, introduced computational methods for agents to learn optimal behaviors through trial and error. However, traditional RL was initially focused on single-agent environments, where the dynamics were stationary and not influenced by other agents.
The integration of game theory with RL emerged as a response to the need for solving multi-agent problems, where interactions between agents create complex, dynamic, and often non-stationary environments. Game-theoretic concepts like Nash equilibrium, cooperative strategies, and zero-sum dynamics were found to be highly relevant for designing and analyzing multi-agent RL algorithms. This synergy between game theory and RL has enabled the development of algorithms capable of addressing challenges such as competition, collaboration, negotiation, and shared-resource optimization in dynamic environments.
Today, the combination of game theory and RL is critical for solving real-world problems that involve multiple autonomous entities. Applications include autonomous driving, where vehicles must coordinate to ensure safety and efficiency; smart grids, where energy consumers and producers interact to optimize power distribution; and robotics, where teams of robots collaborate to achieve shared objectives. These applications often involve dynamic, uncertain, and multi-objective scenarios, where each agent's actions influence and are influenced by others.
This section explores the mathematical foundations of game theory as applied to RL, focusing on stochastic games and payoff maximization in zero-sum and non-zero-sum settings. Key equilibrium strategies, such as Nash equilibrium, Bayesian equilibrium, and Stackelberg equilibrium, are discussed, providing insights into how agents can make optimal decisions in multi-agent environments. These theoretical principles are paired with practical implementations in Rust, demonstrating how game theory can be leveraged to design dynamic, adaptive systems that excel in complex, multi-agent scenarios. Through this lens, the historical evolution of game theory in RL highlights its role as a bridge between mathematical rigor and real-world problem-solving.
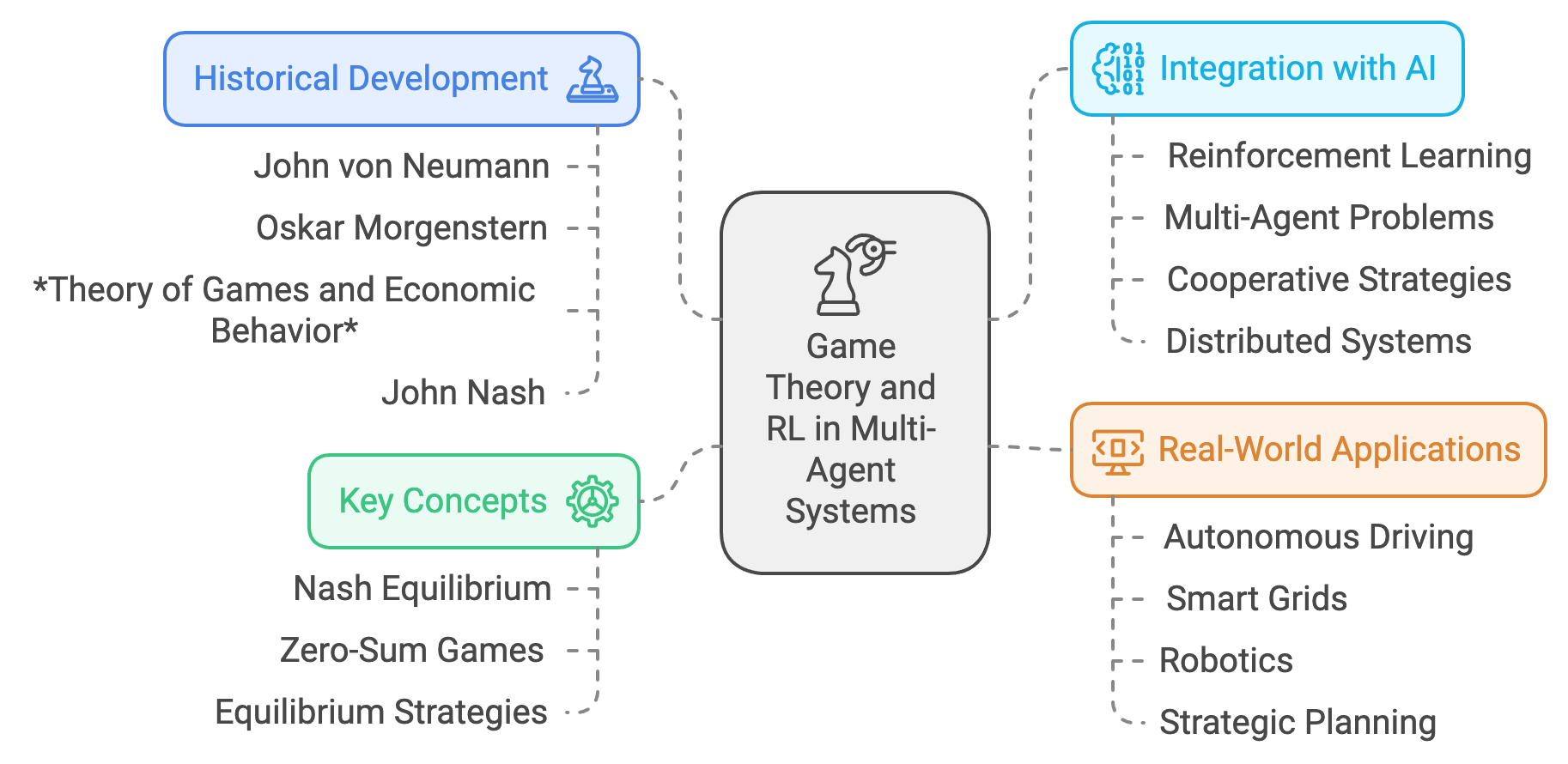
Figure 7: Scopes of Game Theory and RL in MAS.
In a stochastic game, the interaction between agents unfolds over a sequence of states. Formally, a stochastic game is defined as:
$$ G = \langle \mathcal{N}, \mathcal{S}, \{\mathcal{A}_i\}_{i \in \mathcal{N}}, \mathcal{P}, \mathcal{R}, \gamma \rangle, $$
where $\mathcal{N}$ is the set of agents, $\mathcal{S}$ is the finite set of states, and $\mathcal{A}_i$ is the set of actions available to agent $i$. The state transition probability $\mathcal{P}(s' \mid s, \mathbf{a})$ defines the likelihood of transitioning to state $s'$ from $s$ under joint action $\mathbf{a} = (a_1, \ldots, a_n)$. The reward function $\mathcal{R}_i(s, \mathbf{a})$ specifies the reward received by agent $i$ in state $s$ after executing $\mathbf{a}$. The discount factor $\gamma \in [0, 1)$ balances the importance of immediate and future rewards. Each agent seeks to maximize its cumulative discounted reward:
$$ \max_{\pi_i} \mathbb{E} \left[ \sum_{t=0}^\infty \gamma^t \mathcal{R}_i(s_t, \mathbf{a}_t) \right], $$
where $\pi_i: \mathcal{S} \to \mathcal{A}_i$ is the policy of agent $i$.
In zero-sum games, the rewards of all agents sum to zero for any state-action pair, i.e., $\sum_{i \in \mathcal{N}} \mathcal{R}_i(s, \mathbf{a}) = 0$. The optimal strategy involves the Minimax principle, where each agent minimizes its maximum possible loss. This is expressed as:
$$ \min_{\pi_i} \max_{\pi_{-i}} \mathcal{R}_i(s, \mathbf{a}), $$
where $\pi_{-i}$ represents the strategies of all agents except $i$. Non-zero-sum games allow for more diverse interactions, including cooperative and competitive behaviors, as agents seek to maximize individual payoffs while considering interdependencies.
Equilibrium concepts are central to game theory. A Nash Equilibrium is a strategy profile $(\pi_1^, \ldots, \pi_n^)$ where no agent can unilaterally improve its payoff:
$$ \mathcal{R}_i(\pi_i^*, \pi_{-i}^*) \geq \mathcal{R}_i(\pi_i, \pi_{-i}^*), \quad \forall i, \pi_i. $$
In games with incomplete information, Bayesian Equilibria optimize expected payoffs based on probabilistic beliefs about others' strategies. Stackelberg Equilibria extend this by modeling hierarchical interactions, where a leader optimizes its strategy, anticipating the followers’ best responses.
Reinforcement learning enhances MAS by allowing agents to learn equilibrium strategies dynamically. In multi-agent Q-learning, agents iteratively update their value functions based on observed rewards and transitions. The Q-function for agent iii is defined as:
$$ Q_i(s, \mathbf{a}) \leftarrow Q_i(s, \mathbf{a}) + \alpha \left[ \mathcal{R}_i(s, \mathbf{a}) + \gamma \max_{a_i'} Q_i(s', (a_i', \mathbf{a}_{-i})) - Q_i(s, \mathbf{a}) \right], $$
where $\alpha$ is the learning rate, and $\mathbf{a}_{-i}$ denotes the actions of agents other than $i$.
In dynamic environments, equilibria may evolve due to fluctuating conditions or adaptive agent strategies. Evolutionary game theory models this adaptation, where the proportion $x_i$ of agents using strategy $i$ evolves according to replicator dynamics:
$$ \dot{x}_i = x_i \left( \mathbb{E}[R_i] - \mathbb{E}[R] \right), $$
where $\mathbb{E}[R_i]$ is the expected reward of strategy $i$, and $\mathbb{E}[R]$ is the population average reward.
These principles are vital in applications such as supply chain optimization, where agents negotiate prices and allocate resources, and energy markets, where producers and consumers balance supply and demand.
The following Rust implementation combines stochastic games, dynamic strategic interactions, and evolutionary dynamics. The code demonstrates a simple reinforcement learning setup in a discrete game environment. The environment consists of states and actions, with predefined rewards and transitions that guide an agent's interactions. The agent employs Q-learning, a foundational reinforcement learning algorithm, to learn an optimal policy by iteratively updating its Q-values based on the rewards received and the future expected rewards.
use rand::Rng;
use std::collections::HashMap;
/// Define the Game Environment
struct GameEnvironment {
_states: Vec<String>, // Prefix with `_` to suppress unused warning
rewards: HashMap<(String, String), f64>,
transitions: HashMap<(String, String), String>,
}
impl GameEnvironment {
fn new() -> Self {
let states = vec!["S1".to_string(), "S2".to_string()];
let mut rewards = HashMap::new();
rewards.insert(("S1".to_string(), "A1".to_string()), 10.0);
rewards.insert(("S1".to_string(), "A2".to_string()), 5.0);
rewards.insert(("S2".to_string(), "A1".to_string()), 7.0);
rewards.insert(("S2".to_string(), "A2".to_string()), 8.0);
let mut transitions = HashMap::new();
transitions.insert(("S1".to_string(), "A1".to_string()), "S2".to_string());
transitions.insert(("S1".to_string(), "A2".to_string()), "S1".to_string());
transitions.insert(("S2".to_string(), "A1".to_string()), "S1".to_string());
transitions.insert(("S2".to_string(), "A2".to_string()), "S2".to_string());
Self {
_states: states, // Store states but don't use directly
rewards,
transitions,
}
}
fn get_reward(&self, state: &String, action: &String) -> f64 {
*self.rewards.get(&(state.clone(), action.clone())).unwrap_or(&0.0)
}
fn get_next_state(&self, state: &String, action: &String) -> String {
self.transitions
.get(&(state.clone(), action.clone()))
.unwrap_or(state)
.clone()
}
}
/// Define an Agent
struct Agent {
_id: usize, // Prefix with `_` to suppress unused warning
q_table: HashMap<(String, String), f64>,
actions: Vec<String>,
}
impl Agent {
fn new(id: usize, actions: Vec<String>) -> Self {
Self {
_id: id, // Store the ID but don't use directly
q_table: HashMap::new(),
actions,
}
}
fn select_action(&self, _state: &String) -> String { // Prefix `_` to suppress unused warning
let mut rng = rand::thread_rng();
self.actions[rng.gen_range(0..self.actions.len())].clone()
}
fn update_q_value(&mut self, state: &String, action: &String, reward: f64, next_state: &String) {
let alpha = 0.1;
let gamma = 0.9;
let max_next_q = self
.q_table
.iter()
.filter(|((s, _), _)| s == next_state)
.map(|(_, &q)| q)
.fold(0.0, f64::max);
let q = self
.q_table
.entry((state.clone(), action.clone()))
.or_insert(0.0);
*q += alpha * (reward + gamma * max_next_q - *q);
}
}
/// Main Simulation
fn main() {
let env = GameEnvironment::new();
let mut agent = Agent::new(1, vec!["A1".to_string(), "A2".to_string()]);
let mut state = "S1".to_string();
for _ in 0..10 {
let action = agent.select_action(&state);
let reward = env.get_reward(&state, &action);
let next_state = env.get_next_state(&state, &action);
agent.update_q_value(&state, &action, reward, &next_state);
state = next_state;
println!("State: {}, Action: {}, Reward: {}", state, action, reward);
}
}
The program initializes a GameEnvironment with two states (S1, S2), two actions (A1, A2), and mappings for rewards and state transitions. An Agent is then defined, equipped with a Q-table for storing learned state-action values. During each iteration, the agent selects an action randomly, receives a reward based on the current state-action pair, and transitions to the next state. The Q-value for the selected action is updated using the Q-learning update rule, which incorporates the immediate reward and the maximum future reward. Over multiple iterations, the agent refines its policy, aiming to maximize cumulative rewards. This process showcases the core mechanics of reinforcement learning in a simplified environment.
Game theory provides a powerful lens for understanding and engineering strategic interactions in MAS. Through mathematical formalism, concepts such as stochastic games, Nash equilibria, and evolutionary dynamics provide foundational tools for analyzing multi-agent behaviors. By integrating these principles with reinforcement learning, MAS can adapt dynamically to complex and uncertain environments. The Rust implementation demonstrates these concepts in action, showcasing the versatility of game-theoretic approaches in real-world scenarios such as optimization and resource allocation. This synthesis of theory and practice equips readers to design scalable and adaptive multi-agent systems.
11.5. Multi-Agent Reinforcement Learning Algorithms
The concept of Multi-Agent Reinforcement Learning (MARL) arises from the intersection of reinforcement learning (RL) and multi-agent systems (MAS), driven by the need to solve problems involving multiple interacting agents in complex, dynamic environments. The historical journey of MARL begins with the evolution of RL, which was initially designed for single-agent scenarios. In traditional RL, the agent interacts with a static environment, learns to maximize cumulative rewards, and adapts to environmental dynamics that remain largely unaffected by the agent's actions. While effective for tasks like game playing, robotics, and control systems, single-agent RL is limited in scope when applied to systems where multiple autonomous entities coexist and interact.
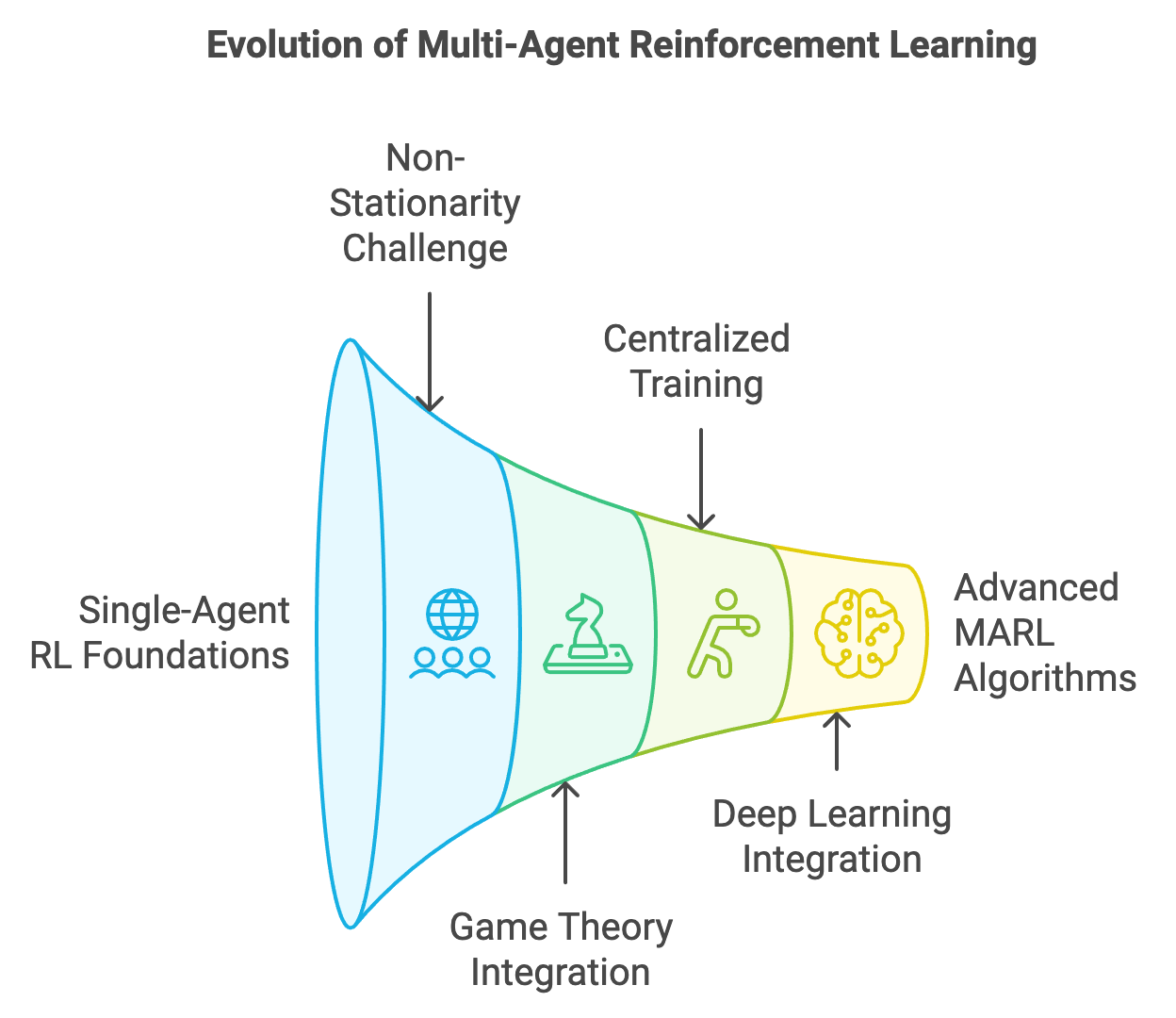
Figure 8: From single-agent to multi-agent RL algorithms.
The foundations of RL were laid in the mid-20th century, with Richard Bellman’s principle of optimality and the development of dynamic programming methods. These ideas evolved into more scalable approaches like Q-learning and policy gradient methods, enabling RL to tackle larger and more complex problems. However, in systems with multiple agents, the environment becomes inherently non-stationary from the perspective of each agent. This is because the strategies and behaviors of other agents are continually evolving, creating a dynamic and unpredictable interaction space. Such non-stationarity presents challenges for traditional RL methods, which assume a static or predictable environment.
The need to address these challenges became evident as researchers and practitioners sought to apply RL to multi-agent domains, such as autonomous driving, drone swarms, and competitive games. Early attempts to extend RL to multi-agent settings involved naïve approaches like treating other agents as part of the environment or assuming static policies for opponents. These methods often failed to scale or generalize to real-world scenarios where agents must adapt to each other dynamically.
The formalization of MARL emerged in the late 20th century with the advent of stochastic games (a generalization of Markov Decision Processes for multiple agents) and the incorporation of game theory to model strategic interactions. Game-theoretic concepts like Nash equilibrium provided a theoretical framework for analyzing multi-agent behavior, particularly in competitive or cooperative settings. Building on these foundations, MARL introduced algorithms specifically designed to handle the complexities of multi-agent systems, such as learning in the presence of other adaptive agents and aligning individual and collective objectives.
In the early 2000s, the introduction of centralized training with decentralized execution (CTDE) marked a significant milestone in MARL. This paradigm allows agents to leverage shared information during training while maintaining autonomy during execution. Algorithms like Multi-Agent Deep Deterministic Policy Gradient (MADDPG) and QMIX emerged from this framework, enabling agents to learn policies that balance individual goals with global cooperation. MADDPG extended policy gradient methods to multi-agent continuous action spaces, while QMIX introduced value decomposition networks for cooperative tasks, ensuring efficient credit assignment among agents.
As neural networks became the backbone of modern RL, MARL evolved further with the integration of deep learning. Techniques like Multi-Agent Actor-Critic (MAAC) incorporated neural networks to approximate policies and value functions, addressing scalability and computational challenges. Advances in deep MARL also introduced methods for modeling opponents, overcoming non-stationarity through adaptive learning, and assigning credit in cooperative scenarios using techniques like counterfactual reasoning.
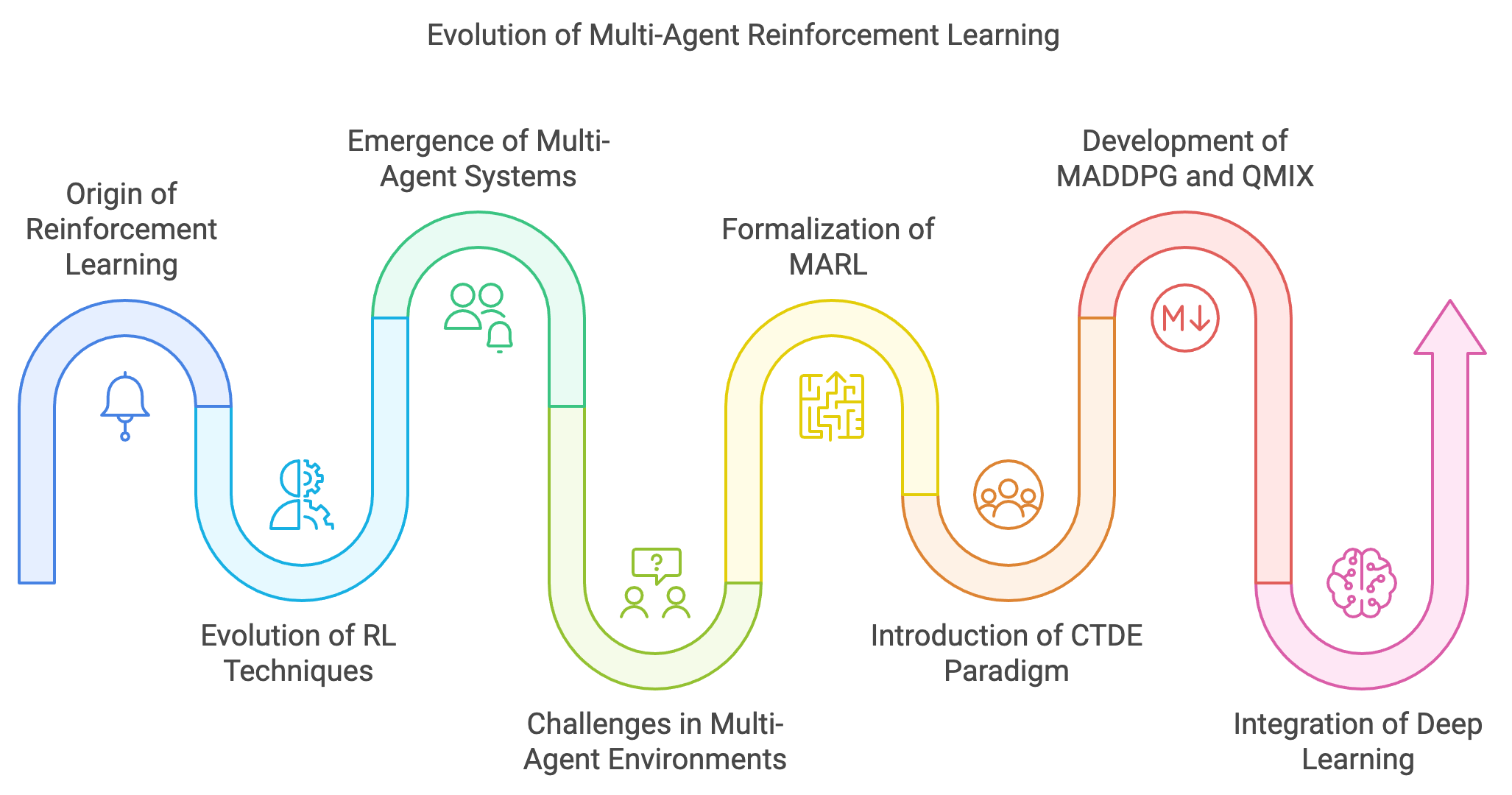
Figure 9: The historical evolution of MARL.
The motivation behind MARL lies in its applicability to real-world problems where agents must operate in shared, uncertain, and dynamic environments. For instance, in autonomous transportation systems, vehicles must coordinate to optimize traffic flow while avoiding collisions. In robotics, teams of drones or robots must collaborate to perform tasks like search and rescue or warehouse automation. These systems require agents to learn not only how to interact with their environment but also how to adapt to and influence the behavior of other agents.
This section explores the foundational algorithms and paradigms that have shaped MARL, including Multi-Agent Deep Q-Networks (MADQN), MADDPG, and QMIX. It delves into centralized and decentralized training approaches, policy gradient methods like Multi-Agent Actor-Critic (MAAC), and advanced techniques for overcoming the challenges of non-stationarity, opponent modeling, and credit assignment. By pairing these theoretical insights with practical implementations in Rust using state-of-the-art neural network libraries, the discussion highlights how MARL bridges the gap between theory and real-world application, enabling the development of robust, adaptive, and scalable multi-agent systems.
MADQN extends Deep Q-Networks (DQN) to multi-agent settings by training independent Q-functions for each agent. Let $Q_i(s, a)$ denote the Q-function for agent $i$, where $s$ is the state and $a$ is the joint action of all agents. The Bellman update for $Q_i$ is given by:
$$ Q_i(s, a) \leftarrow Q_i(s, a) + \alpha \left[ r_i + \gamma \max_{a_i'} Q_i(s', (a_i', a_{-i})) - Q_i(s, a) \right], $$
where $a_{-i}$ denotes the actions of all agents except $i$, $r_i$ is the reward for agent $i$, $\alpha$ is the learning rate, and $\gamma$ is the discount factor.
MADDPG is an actor-critic algorithm tailored for continuous action spaces in MARL. Each agent has an actor $\mu_i$ and a critic $Q_i$. The actor $\mu_i$ maps states to actions, while the critic evaluates the Q-value of the joint action:
$$ Q_i(s, a) = \mathbb{E}_{s'} \left[ r_i + \gamma Q_i(s', a') \mid a' = (\mu_1(s'), \ldots, \mu_n(s')) \right]. $$
MADDPG leverages centralized critics during training, while actors operate in a decentralized manner during execution.
QMIX is a value-based MARL algorithm for cooperative tasks. It uses a mixing network to combine individual Q-values $Q_i(s, a_i)$ into a global Q-value $Q_{\text{tot}}(s, a)$ that satisfies the monotonicity constraint:
$$ \frac{\partial Q_{\text{tot}}}{\partial Q_i} \geq 0, \quad \forall i. $$
This constraint ensures that the global Q-value is an increasing function of individual Q-values, allowing independent Q-learning updates for agents while maintaining a global perspective.
Centralized training with decentralized execution (CTDE) is a common paradigm in MARL. During training, all agents share global information, enabling the use of joint reward functions and centralized critics. During execution, agents operate independently using their learned policies. Formally, the centralized critic for agent $i$ evaluates:
$$ Q_i^{\text{centralized}}(s, a) = \mathbb{E} \left[ \sum_{t=0}^\infty \gamma^t r_i(s_t, a_t) \mid s_0 = s, a_0 = a \right]. $$
Decentralized training, by contrast, relies on local observations and rewards, which may lead to suboptimal performance due to partial observability and non-stationarity.
Non-stationarity in MARL arises from the evolving policies of agents, which alter the dynamics of the environment. Experience replay helps mitigate this by storing interactions in a buffer and sampling uniformly for training, reducing temporal correlations. Additionally, shared environments, where agents interact in the same simulated space, promote stable learning by providing consistent state transitions and rewards.
Opponent modeling further addresses non-stationarity by predicting the strategies of other agents. For example, an opponent model $\hat{\pi}_{-i}$ approximates the policies of other agents, enabling agent $i$ to adapt its strategy dynamically:
$$ Q_i(s, a) = \mathbb{E}_{\hat{\pi}_{-i}} \left[ r_i + \gamma Q_i(s', \hat{a}_{-i}') \right], $$
where $\hat{a}_{-i}'$ is the predicted action of other agents.
This implementation demonstrates two advanced reinforcement learning (RL) techniques for multi-agent systems: Multi-Agent Deep Deterministic Policy Gradient (MADDPG) and QMIX, using the tch crate for neural network operations. MADDPG extends the Deep Deterministic Policy Gradient (DDPG) algorithm to multi-agent scenarios by training centralized critics for each agent, allowing them to learn policies based on global state and action information while maintaining decentralized execution. QMIX, on the other hand, uses a value-based approach with a central mixing network that combines individual agent value functions into a global value function, ensuring monotonicity to preserve optimal joint action selection.
[dependencies]
tch = "0.12.0"
use tch::{nn, nn::ModuleT, nn::OptimizerConfig, Device, Kind, Tensor};
/// Define the Actor-Critic Model
struct ActorCritic {
actor: nn::Sequential,
critic: nn::Sequential,
}
impl ActorCritic {
fn new(vs: &nn::Path, state_dim: i64, action_dim: i64) -> Self {
let actor = nn::seq()
.add(nn::linear(vs / "actor1", state_dim, 128, Default::default()))
.add_fn(|x| x.relu())
.add(nn::linear(vs / "actor2", 128, action_dim, Default::default()))
.add_fn(|x| x.softmax(-1, Kind::Float)); // Action probabilities
let critic = nn::seq()
.add(nn::linear(vs / "critic1", state_dim + action_dim, 128, Default::default()))
.add_fn(|x| x.relu())
.add(nn::linear(vs / "critic2", 128, 1, Default::default())); // Q-value output
Self { actor, critic }
}
fn forward_actor(&self, state: &Tensor) -> Tensor {
self.actor.forward_t(state, false)
}
fn forward_critic(&self, state: &Tensor, action: &Tensor) -> Tensor {
let input = Tensor::cat(&[state, action], 1);
self.critic.forward_t(&input, false)
}
}
/// Define the Environment
struct Environment {
state: Tensor,
_num_agents: usize, // Prefix with an underscore to suppress warnings
}
impl Environment {
fn new(num_agents: usize, state_dim: i64) -> Self {
Self {
state: Tensor::randn(&[num_agents as i64, state_dim], (Kind::Float, Device::Cpu)),
_num_agents: num_agents,
}
}
fn step(&mut self, actions: &Tensor) -> (Tensor, Tensor) {
// Match action dimensions to state dimensions if needed
let action_adjusted = actions.slice(1, 0, self.state.size()[1], 1);
let rewards = action_adjusted.sum_dim_intlist(&[1i64][..], true, Kind::Float); // Sum of actions as reward
self.state += action_adjusted; // Update state based on adjusted actions
(
self.state.copy(), // Next state
rewards, // Rewards for all agents
)
}
}
fn main() {
// Initialize variables
let device = Device::cuda_if_available();
let vs = nn::VarStore::new(device);
let state_dim = 3;
let action_dim = 3; // Match action_dim with state_dim to avoid dimension mismatch
let num_agents = 2;
// Create actor-critic models for each agent
let actor_critic1 = ActorCritic::new(&(&vs.root() / "agent1"), state_dim, action_dim);
let actor_critic2 = ActorCritic::new(&(&vs.root() / "agent2"), state_dim, action_dim);
// Optimizers for actor-critic models
let mut optimizer1 = nn::Adam::default().build(&vs, 1e-3).unwrap();
let mut optimizer2 = nn::Adam::default().build(&vs, 1e-3).unwrap();
// Initialize environment
let mut env = Environment::new(num_agents, state_dim);
// Training loop
for episode in 0..1000 {
let state = env.state.copy();
// Agents select actions
let action1_probs = actor_critic1.forward_actor(&state.narrow(0, 0, 1));
let action2_probs = actor_critic2.forward_actor(&state.narrow(0, 1, 1));
// Sample actions from probabilities
let action1_idx = action1_probs.multinomial(1, true).to_kind(Kind::Int64);
let action2_idx = action2_probs.multinomial(1, true).to_kind(Kind::Int64);
let action1 = Tensor::zeros(&[1, action_dim], (Kind::Float, device))
.scatter(1, &action1_idx, &Tensor::ones(&[1, action_dim], (Kind::Float, device)));
let action2 = Tensor::zeros(&[1, action_dim], (Kind::Float, device))
.scatter(1, &action2_idx, &Tensor::ones(&[1, action_dim], (Kind::Float, device)));
// Clone tensors to avoid ownership issues
let actions = Tensor::cat(&[action1.shallow_clone(), action2.shallow_clone()], 0);
// Step environment
let (_next_state, rewards) = env.step(&actions);
// Compute and update critics
let q_value1 = actor_critic1.forward_critic(&state.narrow(0, 0, 1), &action1);
let q_value2 = actor_critic2.forward_critic(&state.narrow(0, 1, 1), &action2);
let target1 = rewards.narrow(0, 0, 1);
let target2 = rewards.narrow(0, 1, 1);
let critic_loss1 = (&q_value1 - &target1).pow_tensor_scalar(2).mean(Kind::Float);
let critic_loss2 = (&q_value2 - &target2).pow_tensor_scalar(2).mean(Kind::Float);
optimizer1.zero_grad();
critic_loss1.backward();
optimizer1.step();
optimizer2.zero_grad();
critic_loss2.backward();
optimizer2.step();
if episode % 100 == 0 {
println!(
"Episode: {}, Critic Loss1: {:.4}, Critic Loss2: {:.4}",
episode,
critic_loss1.double_value(&[]),
critic_loss2.double_value(&[])
);
}
}
}
MADDPG operates by training decentralized actor networks for each agent that determine their individual actions, while a centralized critic network evaluates the joint state-action value. This allows agents to cooperate effectively by learning from the collective behavior of all agents. QMIX, in contrast, focuses on cooperative tasks by training agents with individual Q-value networks that are combined via a monotonic mixing network to produce a global Q-value, ensuring that agents align their strategies for the joint reward. Both methods leverage neural networks to approximate policies (MADDPG) or Q-values (QMIX), and the tch crate provides efficient tensor operations and backpropagation for optimizing these networks. By employing centralized training and decentralized execution, these approaches are well-suited for complex multi-agent environments with interdependent dynamics.
Multi-Agent Reinforcement Learning algorithms extend classical RL techniques to dynamic, multi-agent environments. By integrating concepts like MADDPG and QMIX with techniques for addressing non-stationarity and assigning credit in cooperative tasks, MARL provides robust frameworks for solving complex, real-world problems. The Rust implementation demonstrates these principles, offering a scalable and practical foundation for developing advanced MARL systems.
11.6. Learning in Cooperative and Competitive MAS
In Multi-Agent Systems (MAS), the dynamics of interactions among agents often mirror real-world human and organizational behaviors, which can generally be categorized as either cooperative or competitive. These dynamics shape the strategies agents employ to learn, adapt, and achieve their objectives within shared environments. By understanding the underlying principles of these learning paradigms, we can design systems that mimic teamwork, rivalry, negotiation, and other forms of interaction in the natural world.
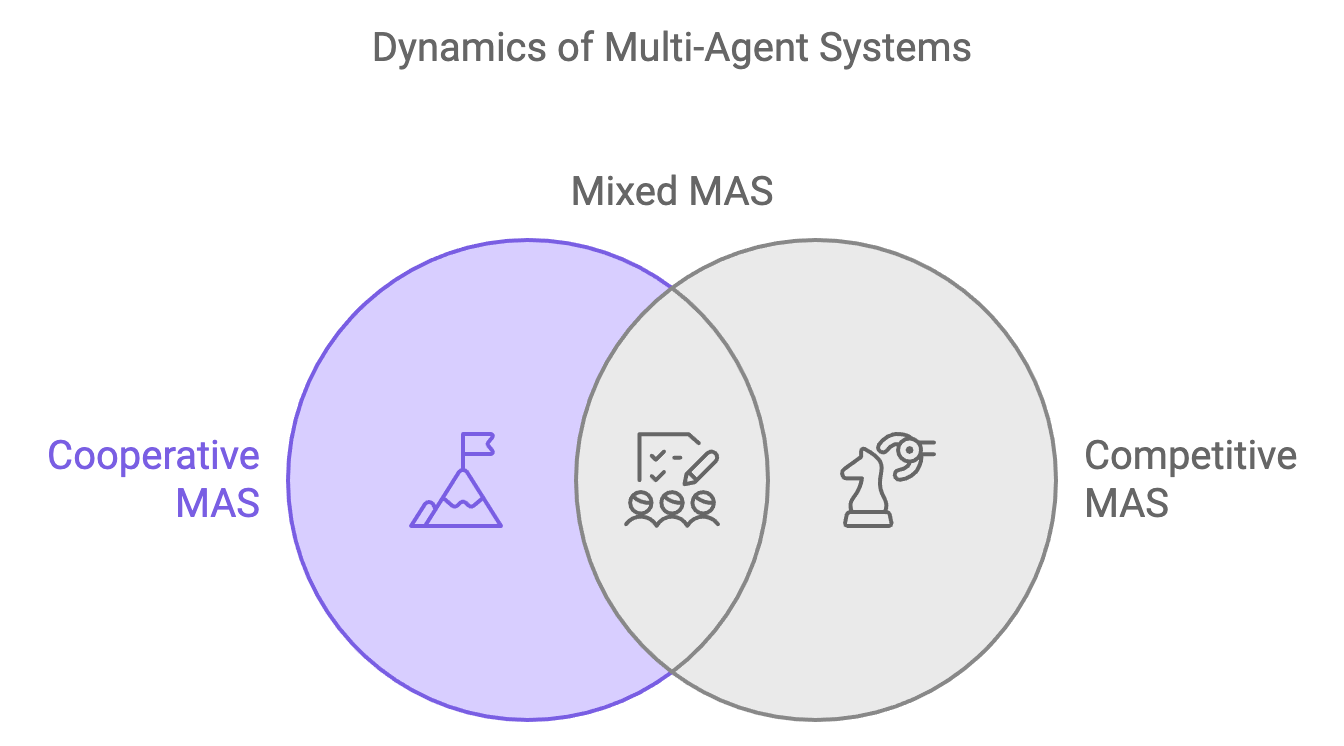
Figure 10: The dynamics of MAS - Cooperative vs Competitive.
Cooperative MAS are analogous to a group of climbers tied together on a mountain expedition. Each climber (agent) must align their actions to ensure the group's safety and success, as they are collectively striving to reach the summit. In this scenario, the agents benefit from shared rewards and must learn joint policies that balance individual contributions with the overall success of the group. This cooperation is not only about achieving the shared objective but also about ensuring efficient collaboration under constraints, such as limited resources or varying skill levels. In practice, cooperative MAS find applications in swarm robotics, where drones must coordinate to search an area or deliver supplies, and in smart grids, where households collectively optimize energy consumption.
On the other hand, competitive MAS resemble a chess match, where each player's (agent's) goal is to outwit the other to secure victory. Here, the environment is inherently adversarial, as one agent's success often comes at the expense of another. These systems require agents to anticipate and counteract the strategies of their opponents while optimizing their own actions. Competitive MAS are prevalent in domains such as autonomous trading, where agents represent competing buyers and sellers in financial markets, and strategic games like StarCraft, where agents control factions vying for dominance.
Cooperation and competition also coexist in mixed settings, akin to a negotiation table where participants may have overlapping goals but also compete for the best possible individual outcome. For instance, autonomous vehicles at an intersection must cooperate to avoid collisions while competing for minimal wait times. In such scenarios, MAS must balance collaboration with self-interest, employing sophisticated frameworks to adapt dynamically to the behaviors of other agents.
To foster cooperation, concepts like reward shaping are employed, where the reward signal is designed to encourage behaviors that align with group objectives. For example, in a multi-robot warehouse, rewards can be distributed based on the successful delivery of packages rather than individual task completion, promoting teamwork over isolated achievements. Similarly, Pareto efficiency is used as a guiding principle to ensure that no agent can improve its outcome without negatively impacting another, facilitating fairness and synergy in cooperative settings.
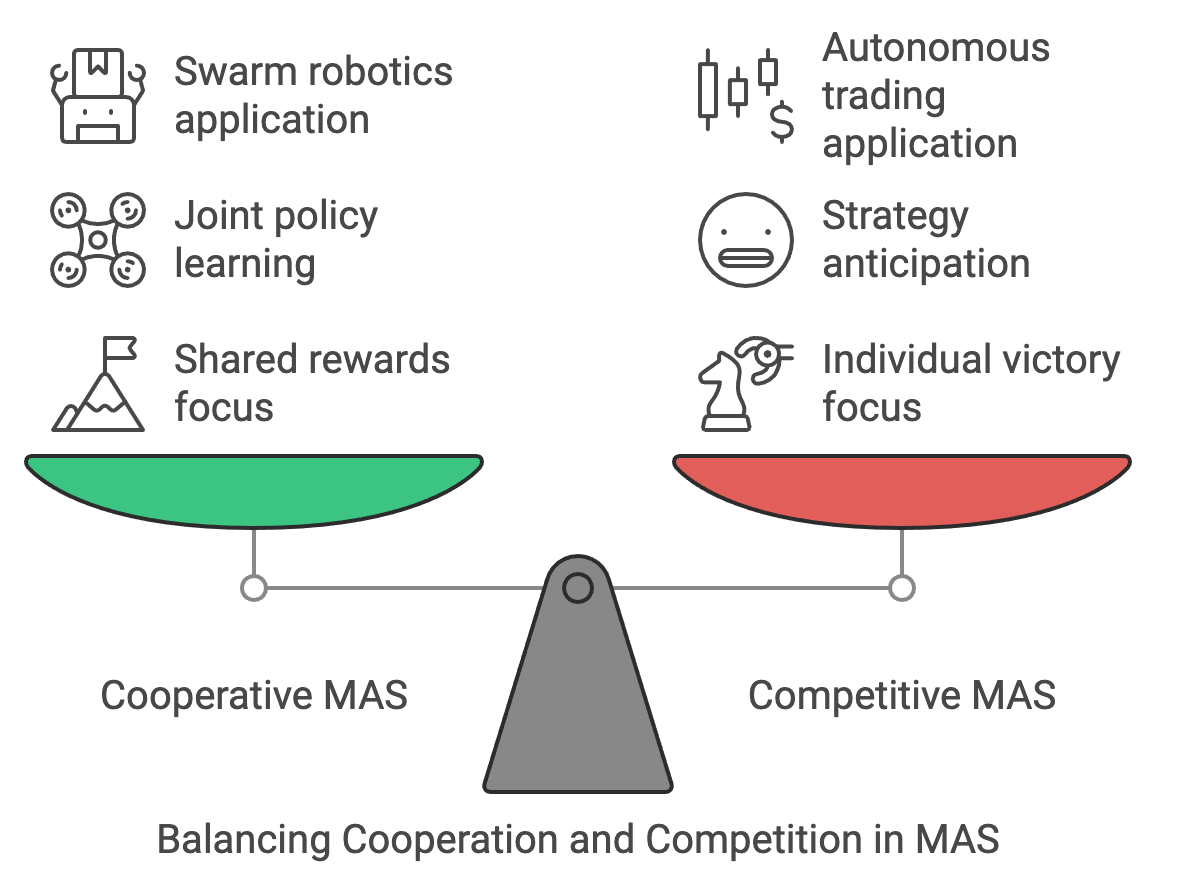
Figure 11: Balance between cooperation and competitive MAS.
In competitive frameworks, agents adopt strategies that anticipate and counteract adversarial behaviors. Adversarial learning frameworks, such as those used in Generative Adversarial Networks (GANs), provide a structure for training agents in competitive environments by pitting them against each other in a zero-sum dynamic. For example, in cybersecurity, defensive agents can be trained to thwart attacks from adversarial agents, simulating real-world hacking attempts to improve system resilience.
Practical implementations of these principles in Rust provide an excellent foundation for building MAS. Rust's performance and concurrency features make it well-suited for scaling multi-agent simulations, whether they involve large-scale cooperation, as in swarm robotics, or adversarial interactions, as in automated game playing. Through hands-on implementations, developers can create systems that demonstrate emergent behaviors, adapt to dynamic conditions, and balance competing objectives in complex, real-world environments. By integrating these foundational concepts into Rust-based applications, the discussion connects theoretical insights to practical innovations in multi-agent system design.
In cooperative MAS, agents collaborate to maximize social welfare, defined as the aggregate utility across all agents. Let $\mathcal{N}$ represent the set of agents, $u_i$ denote the utility function of agent $i$, and $\mathbf{u} = (u_1, u_2, \ldots, u_n)$ be the utility vector. Social welfare is given by:
$$ W(\mathbf{u}) = \sum_{i \in \mathcal{N}} u_i. $$
A solution is Pareto efficient if there exists no alternative utility vector $\mathbf{u}'$ such that $u_i' \geq u_i$ for all $\in \mathcal{N}$ and $u_j' > u_j$ for at least one $j$. Pareto efficiency ensures that resources are allocated optimally across agents.
Reward shaping aligns individual agent incentives with collective objectives by modifying reward functions. If $\mathcal{R}_i(s, \mathbf{a})$ is the original reward for agent $i$ in state $s$ under joint action $\mathbf{a}$, the shaped reward $\mathcal{R}_i'(s, \mathbf{a})$ is:
$$ \mathcal{R}_i'(s, \mathbf{a}) = \mathcal{R}_i(s, \mathbf{a}) + \Phi(s, \mathbf{a}), $$
where $\Phi(s, \mathbf{a})$ is a potential-based shaping function that preserves optimal policies.
Joint policy learning in cooperative MAS involves optimizing a shared policy $\pi$, where:
$$ \pi: \mathcal{S} \to \mathcal{A}, \quad \mathcal{A} = \prod_{i \in \mathcal{N}} \mathcal{A}_i. $$
Value decomposition networks (VDN) decompose the global value function $V_{\text{tot}}$ into agent-specific components:
$$ V_{\text{tot}}(s) = \sum_{i \in \mathcal{N}} V_i(s). $$
This allows decentralized execution while maintaining centralized training.
Competitive MAS model zero-sum or mixed-sum games, where the objectives of agents conflict. In a minimax framework, agent $i$ seeks to minimize the maximum possible loss against an adversary:
$$ \min_{\pi_i} \max_{\pi_{-i}} \mathcal{R}_i(s, \mathbf{a}), $$
where $\pi_{-i}$ represents the joint policies of all other agents. This principle underpins adversarial learning and is often used in reinforcement learning tasks such as generative adversarial networks (GANs) and pursuit-evasion games.
Self-play, a technique widely used in competitive settings, involves agents training against themselves or other instances of the same policy. This iterative process leads to the emergence of robust strategies that generalize well across unseen scenarios.
Emergent properties in MAS arise from simple rules followed by individual agents, resulting in complex global patterns. For example, in cooperative MAS, agents can exhibit flocking or coordinated navigation without explicit central control. In competitive MAS, emergent behaviors often involve strategic deception or adaptive counter-strategies, as seen in adversarial games. Analyzing these behaviors requires tools to capture and quantify group dynamics, such as graph-based metrics or entropy measures.
The following implementation demonstrates cooperative multi-agent pathfinding and competitive adversarial learning in Rust. It uses simple rule-based behaviors to simulate emergent properties and the rand crate for stochastic components. The environment consists of a grid where agents navigate toward randomly assigned goals, with adversarial agents employing predefined strategies to evade or obstruct the cooperative agents. This simulation highlights the interaction dynamics between cooperative and competitive entities, providing insights into emergent behaviors in multi-agent systems.
use rand::Rng;
use std::collections::HashMap;
/// Environment for Multi-Agent Pathfinding
struct Environment {
grid: Vec<Vec<char>>,
agent_positions: HashMap<usize, (usize, usize)>,
goal_positions: HashMap<usize, (usize, usize)>,
}
impl Environment {
fn new(size: usize, num_agents: usize) -> Self {
let mut grid = vec![vec!['.'; size]; size];
let mut agent_positions = HashMap::new();
let mut goal_positions = HashMap::new();
let mut rng = rand::thread_rng();
for agent_id in 0..num_agents {
let agent_pos = (rng.gen_range(0..size), rng.gen_range(0..size));
let goal_pos = (rng.gen_range(0..size), rng.gen_range(0..size));
agent_positions.insert(agent_id, agent_pos);
goal_positions.insert(agent_id, goal_pos);
grid[agent_pos.0][agent_pos.1] = 'A'; // Agent position
grid[goal_pos.0][goal_pos.1] = 'G'; // Goal position
}
Self {
grid,
agent_positions,
goal_positions,
}
}
fn step(&mut self, agent_id: usize, action: (isize, isize)) -> f64 {
let (x, y) = self.agent_positions[&agent_id];
let new_x = ((x as isize + action.0).max(0) as usize).min(self.grid.len() - 1);
let new_y = ((y as isize + action.1).max(0) as usize).min(self.grid[0].len() - 1);
self.grid[x][y] = '.';
self.grid[new_x][new_y] = 'A';
self.agent_positions.insert(agent_id, (new_x, new_y));
if (new_x, new_y) == self.goal_positions[&agent_id] {
return 100.0; // Reward for reaching the goal
}
-1.0 // Penalty for each step
}
fn render(&self) {
for row in &self.grid {
println!("{:?}", row);
}
println!();
}
}
/// Adversarial Agent Model
struct AdversarialAgent {
strategy: fn((usize, usize)) -> (isize, isize),
}
impl AdversarialAgent {
fn new(strategy: fn((usize, usize)) -> (isize, isize)) -> Self {
Self { strategy }
}
fn decide(&self, state: (usize, usize)) -> (isize, isize) {
(self.strategy)(state)
}
}
/// Simple Adversarial Strategy
fn evade_strategy(state: (usize, usize)) -> (isize, isize) {
if state.0 % 2 == 0 {
(0, 1) // Move right
} else {
(1, 0) // Move down
}
}
fn main() {
let mut env = Environment::new(5, 2);
let adversary = AdversarialAgent::new(evade_strategy);
for _ in 0..10 {
env.render();
for agent_id in 0..2 {
let action = adversary.decide(env.agent_positions[&agent_id]);
env.step(agent_id, action);
}
}
}
The implementation simulates a multi-agent system (MAS) with both cooperative and competitive dynamics. In the cooperative pathfinding scenario, agents navigate a shared grid environment to reach their assigned goals while incurring penalties for inefficient movements. The environment rewards agents for successfully reaching their goals, encouraging collaborative and goal-directed behaviors. Simultaneously, the adversarial learning component introduces an adversarial agent that employs a simple evasive strategy to avoid or disrupt cooperative agents. This adversarial behavior is parameterized, allowing the strategy to be easily extended or replaced with more complex behaviors, enabling exploration of competitive tactics in MAS and their impact on overall system dynamics.
The code works by initializing an environment with a grid and assigning random start and goal positions for multiple agents. Each agent follows a sequence of actions, determined by a predefined adversarial strategy, to navigate the grid. The adversarial agents use simple rule-based strategies (like evading by moving in specific directions based on their current state), while the environment rewards or penalizes agents based on their proximity to their goals. The simulation runs in steps, rendering the grid at each iteration to visualize the agents' movements. This implementation provides insights into multi-agent dynamics, emphasizing how simple rule-based behaviors can result in emergent cooperation or competition, and serves as a foundation for more complex multi-agent learning algorithms.
Learning in cooperative and competitive MAS requires blending foundational principles with practical techniques to address diverse challenges. Cooperative systems emphasize joint policy optimization and reward shaping, while competitive environments focus on adversarial strategies and minimax principles. The mathematical rigor of Pareto efficiency and social welfare maximization complements practical implementations, enabling robust simulations of emergent behaviors. The Rust-based implementations demonstrate the versatility of these concepts, providing a foundation for developing scalable and adaptive MAS solutions.
11.7. Applications of Multi-Agent Systems
Multi-Agent Systems (MAS) have become indispensable in addressing complex, real-world problems where traditional centralized approaches fall short. Their ability to distribute decision-making, adapt to dynamic environments, and scale efficiently has positioned MAS as a key enabler in various industries. By integrating with emerging technologies such as the Internet of Things (IoT), edge computing, and machine learning, MAS offers transformative solutions in areas ranging from healthcare and defense to decentralized finance and smart cities.
In healthcare, MAS is revolutionizing patient care and operational efficiency. Autonomous agents, such as robotic assistants, collaborate to perform tasks like surgical assistance, medication delivery, and patient monitoring. For example, in hospital logistics, MAS-powered robots can coordinate to ensure that medical supplies and equipment are optimally distributed across departments, minimizing delays and manual effort. Agents operating in a decentralized fashion can adapt to real-time demands, such as responding to emergencies or reprioritizing delivery routes based on traffic within hospital corridors.
Furthermore, MAS integrates seamlessly with IoT devices in healthcare. Wearable devices and smart sensors, acting as agents, can monitor patients’ vital signs and share data with other agents in the system. For example, in remote patient monitoring for chronic disease management, MAS ensures that critical health data is aggregated, analyzed, and acted upon, enabling timely interventions. Rust's performance and safety features make it an excellent choice for implementing MAS in healthcare, where reliability and efficiency are paramount.
In defense, MAS plays a crucial role in developing autonomous systems for surveillance, reconnaissance, and combat operations. Swarm robotics, inspired by biological systems, is a prime example. Drones operating as a coordinated swarm can efficiently cover large areas for surveillance, detect threats, and adapt to dynamic conditions in the field. Unlike single-agent systems, MAS ensures robustness through redundancy; if one agent fails, others can compensate, maintaining mission integrity.
MAS also enhances decision-making in complex military scenarios, such as coordinating unmanned aerial vehicles (UAVs) with ground and naval units. These systems leverage edge computing to process data locally, reducing latency and enabling real-time responsiveness. For example, in anti-access/area-denial (A2/AD) strategies, MAS can coordinate a fleet of UAVs to disrupt enemy operations while dynamically adapting to changes in the battlefield.
In the financial sector, MAS underpins the operation of decentralized finance (DeFi) systems. Agents in these systems act as autonomous entities, executing trades, managing liquidity, and facilitating transactions without centralized intermediaries. For instance, decentralized exchanges (DEXs) rely on smart contracts and MAS principles to enable peer-to-peer trading of cryptocurrencies. Agents monitor market conditions, execute arbitrage opportunities, and adjust prices based on supply and demand dynamics.
In decentralized lending and borrowing platforms, agents evaluate collateralized loans, manage interest rates, and ensure compliance with the platform's rules. Rust’s safety and concurrency make it a compelling choice for implementing MAS in blockchain applications, where transaction integrity and security are critical.
MAS is a driving force behind the development of smart cities, enabling autonomous coordination of infrastructure and resources. In transportation, MAS powers intelligent traffic management systems where autonomous vehicles act as agents that communicate with each other and with infrastructure, such as traffic lights and road sensors. This coordination reduces congestion, optimizes fuel consumption, and enhances safety.
In energy management, MAS optimizes the operation of smart grids. Agents representing households, businesses, and power generators collaborate to balance energy demand and supply in real-time. For instance, during peak usage hours, agents can negotiate energy usage, enabling load balancing and preventing blackouts. Additionally, MAS facilitates the integration of renewable energy sources by dynamically adjusting to fluctuations in solar and wind energy production.
In agriculture, MAS is transforming precision farming practices by enabling autonomous machines and sensors to work together in monitoring and optimizing crop production. Drones equipped with multispectral sensors act as agents, scanning fields to identify areas needing irrigation, fertilization, or pest control. Ground-based robots collaborate to execute these tasks efficiently, reducing resource waste and improving yields.
MAS also enhances supply chain logistics in agriculture, ensuring that produce is transported and stored under optimal conditions. By coordinating between agents representing farms, warehouses, and retailers, MAS minimizes delays and spoilage, improving overall supply chain efficiency.
In the gaming industry, MAS enables dynamic, immersive experiences by simulating realistic interactions between autonomous agents. For example, in massively multiplayer online games (MMOs), NPCs (non-player characters) can act as intelligent agents that adapt their behavior based on player actions and environmental changes. This enhances the realism and engagement of the gaming experience.
In virtual and augmented reality, MAS powers interactive environments where agents represent virtual assistants, competitors, or collaborators. These systems adapt to user behavior, creating personalized and evolving experiences.
Multi-Agent Systems are reshaping industries by enabling decentralized, adaptive, and scalable solutions to some of the most pressing challenges. From healthcare and defense to finance and agriculture, MAS demonstrates its versatility and transformative potential. By integrating these systems with advanced technologies like IoT and edge computing, and implementing them in Rust for reliability and performance, MAS continues to drive innovation across domains, setting the stage for the next generation of intelligent systems.
Figure 12: Various industry use cases of MAS and RL.
At the core of MAS applications lies the ability to model and optimize complex problems. Consider a task allocation problem where $n$ agents are assigned to $m$ tasks. Let $c_{ij}$ denote the cost of assigning agent $i$ to task $j$. The objective is to minimize the total cost:
$$ \min \sum_{i=1}^n \sum_{j=1}^m x_{ij} c_{ij}, $$
subject to:
$$ \sum_{j=1}^m x_{ij} = 1, \quad \forall i, \quad \text{and} \quad \sum_{i=1}^n x_{ij} = 1, \quad \forall j, $$
where $x_{ij} \in \{0, 1\}$ is a binary variable indicating whether agent $i$ is assigned to task $j$.
For swarm behavior and multi-robot collaboration, agents interact to achieve global objectives, such as coordinated movement or object transport. Each agent follows simple rules, such as alignment, cohesion, and separation, defined mathematically as:
$$ v_i(t+1) = \alpha_a v_{\text{align}} + \alpha_c v_{\text{cohesion}} + \alpha_s v_{\text{separation}}, $$
where $v_{\text{align}}$, $v_{\text{cohesion}}$, and $v_{\text{separation}}$ are velocity components influenced by the neighboring agents, and $\alpha_a, \alpha_c, \alpha_s$ are weights determining the influence of each component.
Data-driven MAS leverage real-world datasets to define problem parameters, constraints, and objectives. For instance, in financial markets, agents simulate trading behaviors based on historical price data, optimizing strategies for profit maximization or risk minimization.
MAS find extensive use in healthcare systems, enabling distributed coordination among autonomous devices for patient monitoring, diagnostics, and treatment planning. For example, MAS can optimize the allocation of medical resources in hospitals during emergencies by balancing demand and availability in real time.
In defense, MAS power drone swarms for surveillance, reconnaissance, and coordinated attacks. These systems rely on decentralized decision-making to maintain resilience in adversarial environments where communication may be disrupted.
Decentralized finance (DeFi) leverages MAS for algorithmic trading, liquidity management, and consensus in blockchain networks. Agents in DeFi applications act autonomously to optimize trading strategies, monitor market conditions, and ensure network security.
MAS also play a vital role in Human-AI collaboration, emphasizing ethical considerations like transparency and trust. For instance, in autonomous driving, MAS ensure the coordination of vehicles while maintaining safety and fairness for all users on the road.
Rust’s memory safety, high performance, and concurrency make it a robust platform for implementing MAS solutions in these industries. Developers can use Rust’s ecosystem, including libraries for networking, distributed systems, and machine learning, to build scalable and secure MAS applications. For example, Rust's concurrency model allows efficient simulation of large-scale MAS, such as swarms of drones or autonomous vehicles. Additionally, its safety guarantees ensure reliability in critical applications like healthcare and defense.
By modeling agents as concurrent actors communicating through message-passing frameworks in Rust, developers can create systems that emulate real-world interactions. For instance, an energy management MAS could leverage Rust’s async programming capabilities to process real-time data from distributed sensors and adjust power distribution dynamically.
The following Rust implementation demonstrates MAS applications in three domains: drone swarms, decentralized blockchain systems, and financial market simulations.
The following code demonstrates a simple swarm intelligence simulation using drones in Rust. Each drone in the swarm interacts with its neighbors to achieve emergent behavior based on three key rules: alignment (matching neighbors' velocity), cohesion (moving toward the center of neighbors), and separation (avoiding crowding). The drones aim to collectively navigate toward a common goal while maintaining swarm dynamics, with some randomness introduced to simulate real-world unpredictability.
use rand::Rng;
#[derive(Debug, Clone)]
struct Drone {
position: (f64, f64),
velocity: (f64, f64),
}
impl Drone {
fn new(x: f64, y: f64) -> Self {
Self {
position: (x, y),
velocity: (0.0, 0.0),
}
}
fn update(&mut self, neighbors: &Vec<Drone>, goal: (f64, f64)) {
let mut rng = rand::thread_rng();
// Alignment: Match velocity of neighbors
let align = neighbors
.iter()
.map(|n| n.velocity)
.fold((0.0, 0.0), |acc, v| (acc.0 + v.0, acc.1 + v.1));
// Cohesion: Move towards center of neighbors
let _center = neighbors
.iter()
.map(|n| n.position)
.fold((0.0, 0.0), |acc, p| (acc.0 + p.0, acc.1 + p.1));
// Separation: Avoid crowding
let separation = neighbors
.iter()
.map(|n| (self.position.0 - n.position.0, self.position.1 - n.position.1))
.fold((0.0, 0.0), |acc, p| (acc.0 + p.0, acc.1 + p.1));
// Combine rules
self.velocity.0 = 0.3 * align.0 + 0.3 * (goal.0 - self.position.0) - 0.2 * separation.0;
self.velocity.1 = 0.3 * align.1 + 0.3 * (goal.1 - self.position.1) - 0.2 * separation.1;
// Add noise for randomness
self.velocity.0 += rng.gen_range(-0.1..0.1);
self.velocity.1 += rng.gen_range(-0.1..0.1);
// Update position
self.position.0 += self.velocity.0;
self.position.1 += self.velocity.1;
}
}
fn main() {
let mut swarm = vec![
Drone::new(0.0, 0.0),
Drone::new(1.0, 1.0),
Drone::new(2.0, 2.0),
];
let goal = (10.0, 10.0);
for _ in 0..10 {
for i in 0..swarm.len() {
let neighbors = swarm.clone();
swarm[i].update(&neighbors, goal);
}
println!("{:?}", swarm);
}
}
The program initializes a swarm of drones, each with an initial position and velocity. In each simulation step, every drone updates its velocity and position based on interactions with its neighbors and the goal location. The velocity is computed as a weighted combination of alignment with neighbors, movement toward the goal, and separation to avoid collisions. Random noise is added to the velocity for variability. The updated velocity is then used to compute the new position. This process is repeated for multiple iterations, and the positions of all drones are printed at each step, showcasing how local interactions and simple rules can produce coordinated swarm behavior.
This implementation simulates a decentralized blockchain network with nodes capable of interacting and maintaining consensus. Each node manages a blockchain ledger, validates proposed transactions using cryptographic hashing, and resolves conflicts through a longest-chain rule. The nodes ensure the integrity of the blockchain by verifying the hash of each block against the previous block, mimicking a simple proof-of-work system. Transactions are tracked to prevent duplicates, and nodes can synchronize their blockchains to resolve inconsistencies.
use std::collections::HashSet;
use sha2::{Sha256, Digest};
#[derive(Debug, Clone)]
struct Node {
id: usize,
blockchain: Vec<String>,
pending_transactions: HashSet<String>,
}
impl Node {
fn new(id: usize) -> Self {
Self {
id,
blockchain: vec!["Genesis Block".to_string()],
pending_transactions: HashSet::new(),
}
}
fn propose_block(&mut self, transaction: &str) -> Option<String> {
if self.pending_transactions.contains(transaction) {
return None; // Avoid duplicate transactions
}
self.pending_transactions.insert(transaction.to_string());
let new_block = format!(
"Block {}: {} | Hash: {}",
self.blockchain.len(),
transaction,
Self::hash_block(self.blockchain.last().unwrap(), transaction)
);
Some(new_block)
}
fn validate_block(&self, block: &String) -> bool {
let parts: Vec<&str> = block.split(" | Hash: ").collect();
if parts.len() != 2 {
return false; // Malformed block
}
let transaction = parts[0];
let expected_hash = Self::hash_block(self.blockchain.last().unwrap(), transaction);
parts[1] == expected_hash
}
fn add_block(&mut self, block: String) {
if self.validate_block(&block) {
self.blockchain.push(block);
}
}
fn resolve_conflicts(&mut self, other: &Node) {
if other.blockchain.len() > self.blockchain.len() {
self.blockchain = other.blockchain.clone();
}
}
fn hash_block(previous_block: &str, transaction: &str) -> String {
let mut hasher = Sha256::new();
hasher.update(previous_block);
hasher.update(transaction);
format!("{:x}", hasher.finalize())
}
}
fn main() {
let mut node1 = Node::new(1);
let mut node2 = Node::new(2);
if let Some(block) = node1.propose_block("Alice pays Bob 10 BTC") {
node2.add_block(block.clone());
node1.add_block(block);
}
if let Some(block) = node2.propose_block("Bob pays Charlie 5 BTC") {
node1.add_block(block.clone());
node2.add_block(block);
}
// Simulate resolving conflicts
node1.resolve_conflicts(&node2);
println!("Node 1 Blockchain: {:?}", node1.blockchain);
println!("Node 2 Blockchain: {:?}", node2.blockchain);
}
Each node proposes a new block containing a transaction, appending it to its local blockchain if the block passes cryptographic validation. The block includes a hash derived from the previous block and the current transaction, ensuring immutability and consistency. Nodes validate blocks from others to maintain trust in the network. A simple conflict resolution mechanism ensures all nodes eventually adopt the longest valid blockchain, simulating decentralized consensus. This implementation demonstrates key blockchain concepts like hashing, validation, and conflict resolution, serving as a foundation for exploring more sophisticated blockchain features.
This code simulates a dynamic financial market where agents (traders) interact based on different trading strategies such as risk-averse, risk-seeking, and neutral behavior. The market price fluctuates in response to aggregate trading activity, incorporating supply-demand dynamics and market volatility. This advanced implementation captures realistic trading patterns and emergent market behavior through its use of probabilistic decision-making and adaptive pricing.
use rand::Rng;
#[derive(Debug)]
struct Trader {
id: usize,
funds: f64,
shares: f64,
strategy: TraderStrategy,
}
#[derive(Debug)]
enum TraderStrategy {
RiskAverse,
RiskSeeking,
Neutral,
}
impl Trader {
fn new(id: usize, funds: f64, strategy: TraderStrategy) -> Self {
Self {
id,
funds,
shares: 0.0,
strategy,
}
}
fn trade(&mut self, market_price: f64) -> f64 {
let mut rng = rand::thread_rng();
let decision = match self.strategy {
TraderStrategy::RiskAverse => rng.gen_bool(0.3), // 30% chance to buy
TraderStrategy::RiskSeeking => rng.gen_bool(0.7), // 70% chance to buy
TraderStrategy::Neutral => rng.gen_bool(0.5), // 50% chance to buy
};
if decision && self.funds > market_price {
// Buy shares
self.shares += 1.0;
self.funds -= market_price;
market_price
} else if self.shares > 0.0 && rng.gen_bool(0.3) {
// Sell shares with 30% chance
self.shares -= 1.0;
self.funds += market_price;
-market_price
} else {
0.0
}
}
}
fn adjust_market_price(market_price: f64, net_demand: f64, volatility: f64) -> f64 {
let adjustment = net_demand * 0.1 + rand::thread_rng().gen_range(-volatility..volatility);
(market_price + adjustment).max(1.0) // Ensure price doesn't drop below 1.0
}
fn main() {
let mut traders = vec![
Trader::new(1, 100.0, TraderStrategy::RiskAverse),
Trader::new(2, 150.0, TraderStrategy::Neutral),
Trader::new(3, 200.0, TraderStrategy::RiskSeeking),
];
let mut market_price = 50.0;
let volatility = 5.0;
for _ in 0..10 {
let mut net_demand = 0.0;
for trader in &mut traders {
net_demand += trader.trade(market_price);
}
// Adjust market price based on net demand and volatility
market_price = adjust_market_price(market_price, net_demand, volatility);
println!("Market Price: {:.2}", market_price);
}
println!("Final Market State:");
for trader in traders {
println!(
"Trader {}: Funds {:.2}, Shares {:.2}",
trader.id, trader.funds, trader.shares
);
}
}
The simulation initializes a set of traders with varying strategies and funds, along with a starting market price. During each trading round, traders decide probabilistically whether to buy or sell shares based on their strategy. Risk-seeking traders are more likely to buy, while risk-averse traders buy less frequently and may prefer holding cash. The net demand (aggregate buy-sell difference) from all trades influences the market price, which is further adjusted by a random volatility factor to simulate real-world price fluctuations. Over multiple rounds, the system reveals how strategy diversity and market dynamics impact individual trader outcomes and the overall market, showcasing the interplay between micro-level decisions and macro-level trends.
In summary of this section, applications of Multi-Agent Systems span a wide array of domains, from drone coordination and blockchain networks to financial market simulations. By leveraging foundational principles like task allocation, swarm behavior, and decentralized collaboration, MAS address complex, dynamic challenges. The Rust implementations demonstrate the versatility and efficiency of MAS in tackling real-world problems, providing robust, scalable, and adaptive solutions.
11.7. Challenges and Future Directions in MAS
As Multi-Agent Systems (MAS) become increasingly complex and diverse in their applications, addressing their inherent challenges is critical to ensuring efficiency, scalability, and robustness. These challenges arise from the computational and algorithmic intricacies of managing interactions among agents in dynamic, often unpredictable environments. By tackling these challenges head-on, MAS can evolve into systems that not only solve today's problems but also adapt to future demands. This section delves into the key challenges, explores conceptual innovations to address them, and highlights practical implementations in Rust for robust and high-performance simulations.
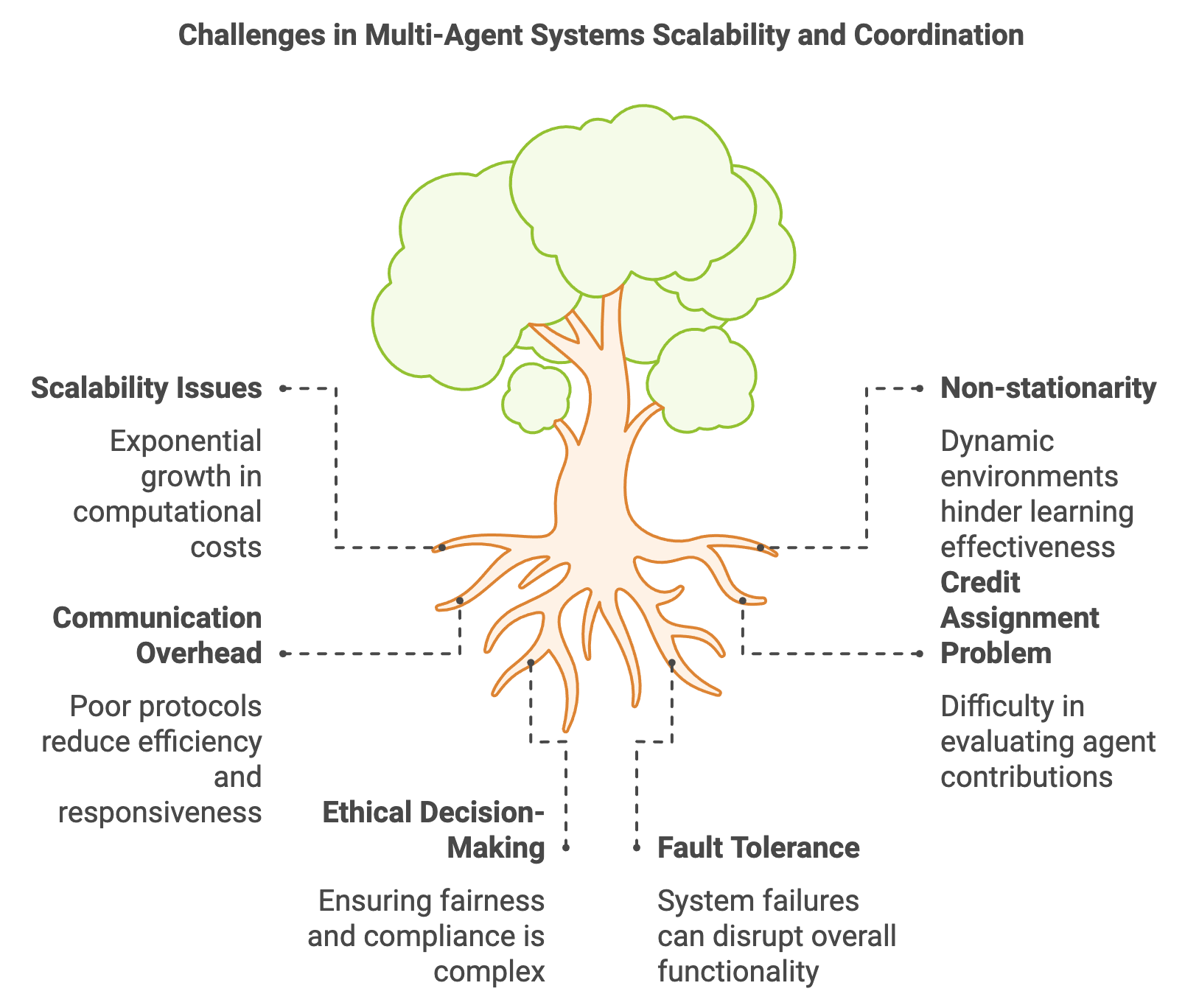
Figure 13: Key challenges of MAS implementation.
One of the most significant challenges in MAS is scalability. As the number of agents in a system increases, the computational cost of managing their interactions grows exponentially. This is often referred to as the "curse of dimensionality," where the state and action spaces expand combinatorially with the number of agents. For instance, in cooperative tasks like swarm robotics or smart grids, the system must process vast amounts of data in real-time to ensure efficient coordination.
To address scalability, MAS research has explored decentralized algorithms that reduce global computational loads by distributing decision-making across agents. However, decentralization introduces trade-offs, such as the need for efficient communication protocols and mechanisms to reconcile conflicting goals. Rust, with its emphasis on performance and memory safety, is well-suited for implementing these distributed architectures. By leveraging Rust’s async programming capabilities and its lightweight concurrency model, developers can build scalable MAS simulations that efficiently handle large agent populations.
In MAS, agents operate in environments that are constantly evolving due to the actions of other agents. This non-stationarity poses significant challenges for learning and decision-making. Traditional reinforcement learning (RL) methods, designed for static environments, often fail in MAS because the dynamics of the environment change as agents adapt their policies.
Overcoming non-stationarity requires algorithms capable of modeling and predicting the behavior of other agents. Techniques like opponent modeling, where agents infer and anticipate the strategies of others, are critical for addressing this challenge. Additionally, approaches such as experience replay with prioritized sampling or using robust training methods that account for dynamic behaviors can mitigate the impact of non-stationarity. Implementing such methods in Rust allows for efficient simulations that can iterate over millions of dynamic interactions while maintaining high performance.
Effective coordination among agents is essential in both cooperative and competitive MAS. However, as the number of agents increases, so does the complexity of ensuring synchronized and meaningful communication. Poorly designed communication protocols can lead to significant overhead, reducing system efficiency and responsiveness.
Graph-based models are commonly used to represent communication in MAS, where nodes represent agents, and edges represent communication links. Message-passing algorithms on these graphs enable agents to share critical information, but designing these algorithms to be both efficient and robust is non-trivial. For example, in a distributed logistics system, agents must exchange route and task information while minimizing latency and bandwidth usage.
Rust’s low-level control over system resources makes it an ideal language for optimizing communication protocols. By using Rust's libraries for networking and distributed systems, developers can implement lightweight, high-performance communication layers that minimize overhead and ensure reliable coordination in large-scale MAS.
In cooperative MAS, a persistent challenge is the assignment of credit or blame for shared outcomes. When agents collectively achieve a goal, determining the contribution of each agent to the success (or failure) is critical for learning and incentivizing desirable behaviors. This is known as the credit assignment problem.
Advanced techniques like value decomposition networks (VDN) and counterfactual multi-agent policy gradients (COMA) have been developed to address this issue. These methods decompose global rewards into individual contributions or use counterfactual reasoning to evaluate how each agent’s actions affect the overall outcome. Implementing such techniques in Rust involves leveraging deep learning libraries like tch to build scalable neural network architectures that can process joint reward signals and assign credit efficiently.
As MAS systems are deployed in critical domains such as healthcare, finance, and autonomous vehicles, ethical and fair decision-making becomes paramount. Ensuring that agents make decisions that align with societal norms, avoid bias, and minimize harm is a multi-faceted challenge.
For example, in autonomous vehicle coordination, MAS must not only optimize traffic flow but also ensure fairness by preventing scenarios where some vehicles are consistently prioritized over others. Similarly, in financial markets, MAS-powered trading agents must adhere to regulatory standards to prevent market manipulation or unfair trading practices.
Ethical decision-making in MAS requires the integration of constraints and objectives into the learning process. Techniques like constrained optimization and reward regularization can be employed to align agent behavior with ethical principles. Rust’s type safety and compile-time guarantees provide a solid foundation for implementing MAS systems where adherence to constraints is critical, ensuring both correctness and reliability.
MAS must remain functional even when individual agents or communication links fail. This challenge is particularly pronounced in distributed systems like drone swarms or smart grids, where the failure of a single component can cascade into system-wide disruptions if not properly handled.
Fault-tolerant MAS employ strategies such as redundancy, adaptive reconfiguration, and consensus algorithms to maintain system integrity. For instance, gossip-based protocols enable robust message propagation even in unreliable networks, ensuring that critical information reaches all agents despite failures. Rust’s ownership model and strong concurrency primitives ensure that fault-tolerant MAS systems are free from common issues like race conditions and deadlocks, making them more reliable in real-world deployments.
While MAS face significant challenges, these obstacles also present opportunities for innovation. Emerging technologies such as edge computing, 5G connectivity, and quantum-inspired algorithms are poised to address many of the current limitations. For example, edge computing can decentralize MAS computations further, reducing latency and enabling real-time decision-making. Quantum-inspired algorithms, with their potential for parallelism and optimization, may unlock new levels of scalability and efficiency in MAS.
Additionally, the integration of self-supervised learning and foundation models into MAS research offers promising avenues for enhancing agent adaptability and decision-making capabilities. By leveraging these advanced paradigms, MAS can evolve into systems that not only learn from their environment but also generalize across tasks and domains, making them more versatile and impactful.
One of the primary challenges in MAS is sample inefficiency, where agents require an extensive amount of data to learn effective policies. In environments with sparse rewards, agents may struggle to converge to optimal strategies. Formally, the expected cumulative reward for agent $i$ over $T$ timesteps is:
$$ \mathbb{E} \left[ \sum_{t=0}^T \gamma^t \mathcal{R}_i(s_t, a_t) \right], $$
where $\mathcal{R}_i(s_t, a_t)$ is the reward function, and $\gamma$ is the discount factor. Sparse rewards $\mathcal{R}_i \approx 0$ for most $s_t, a_t$ combinations lead to slow learning, particularly in high-dimensional state-action spaces.
Scalability is another pressing issue. As the number of agents $N$ grows, the joint action space $\mathcal{A} = \prod_{i=1}^N \mathcal{A}_i$ increases exponentially, leading to the curse of dimensionality. Efficient techniques like value decomposition networks (VDN) and factorized policies help mitigate this but are limited in extremely large systems.
Data sparsity and resource constraints further compound these challenges. In resource-constrained environments, agents compete for limited computational, energy, or communication resources. This can be modeled as a constrained optimization problem:
$$ \max_{\pi_i} \sum_{i=1}^N \mathcal{R}_i(\pi_i) \quad \text{subject to} \quad \sum_{i=1}^N r_i \leq R, $$
where $r_i$ is the resource consumed by agent $i$, and $R$ is the total available resource.
Handling high-dimensional state-action spaces often requires techniques such as dimensionality reduction, hierarchical learning, or attention mechanisms. For example, principal component analysis (PCA) can be used to project high-dimensional state vectors $s \in \mathbb{R}^n$ into a lower-dimensional space $z \in \mathbb{R}^k$ with $k \ll n$:
$$ z = W^\top s, \quad W \in \mathbb{R}^{n \times k}. $$
The future of Multi-Agent Systems (MAS) research is deeply connected with innovations in machine learning, ethical considerations, and emerging computational paradigms. Curriculum and lifelong learning offer a pathway for agents to progressively acquire skills by training on increasingly complex tasks. This approach dynamically adjusts learning objectives $\mathcal{L}$ over time, transitioning from simpler objectives $\mathcal{L}_\text{easy}$ in early phases to more challenging ones $\mathcal{L}_\text{hard}$ in later stages. This progression can be expressed mathematically as $\mathcal{L}(t) = \mathcal{L}_\text{easy}(t) \cdot \mathbb{1}_{\text{early}} + \mathcal{L}_\text{hard}(t) \cdot \mathbb{1}_{\text{late}}$, where $\mathbb{1}_{\text{early}}$ and $\mathbb{1}_{\text{late}}$ denote the phases of task difficulty.
Meta-learning further empowers MAS by equipping agents with the ability to learn new tasks rapidly and adapt to changing environments. This adaptability is achieved by optimizing a meta-objective $\mathcal{L}_\text{meta}$, which aggregates task-specific objectives $\mathcal{L}_i$ over a set of tasks. Formally, this is represented as $\mathcal{L}_\text{meta} = \sum_{i=1}^M \mathcal{L}_i(\theta_i)$, where $\theta_i$ are the parameters specific to task $i$. This framework enables agents to generalize across tasks and environments effectively.
Ethical deployment of autonomous MAS poses significant challenges, particularly in applications like healthcare and autonomous driving. Ensuring fairness, transparency, and accountability necessitates the integration of ethical constraints into agent policies. For example, a learning objective $\mathcal{L}$ can incorporate fairness considerations as $\mathcal{L} = \mathcal{L}_\text{task} + \lambda \mathcal{L}_\text{fairness}$, where $\lambda$ determines the trade-off between task performance and fairness. This ensures that agents not only optimize for utility but also adhere to ethical principles.
Finally, emerging technologies like quantum computing and neuro-symbolic AI present transformative opportunities for MAS. Quantum algorithms can mitigate the combinatorial explosion inherent in multi-agent problems, enabling efficient computation in complex scenarios. Neuro-symbolic AI combines the predictive power of deep learning with the logical reasoning capabilities of symbolic AI, offering enhanced interpretability and efficiency for MAS applications. These synergies promise to drive MAS research and applications into new frontiers, addressing scalability, adaptability, and ethical considerations in unprecedented ways.
This code simulates a multi-agent system (MAS) using principles of Reinforcement Learning (RL) to model agents that interact and adapt within a shared environment. Each agent dynamically updates its state and performs actions based on its local interactions with neighbors. The agents follow a rule-based update mechanism akin to RL policies, where their actions are proportional to the states influenced by the collective behavior of the group. The system demonstrates emergent behavior through decentralized decision-making, showcasing how agents self-organize without centralized control.
use std::sync::{Arc, Mutex};
use std::thread;
use rand::Rng;
use plotters::prelude::*;
/// Define an Agent with a state and action set
struct Agent {
id: usize,
state: f64,
action: f64,
}
impl Agent {
fn new(id: usize) -> Self {
Self {
id,
state: rand::thread_rng().gen_range(0.0..1.0),
action: 0.0,
}
}
fn update_state(&mut self, neighbors: &[f64]) {
self.state = neighbors.iter().copied().sum::<f64>() / neighbors.len() as f64;
self.action = self.state * 2.0; // Simple proportional action
}
}
/// Define the Environment for the agents
struct Environment {
agents: Vec<Arc<Mutex<Agent>>>,
}
impl Environment {
fn new(num_agents: usize) -> Self {
let agents = (0..num_agents)
.map(|id| Arc::new(Mutex::new(Agent::new(id))))
.collect();
Self { agents }
}
/// Step function to update all agents dynamically
fn step(&self) {
for i in 0..self.agents.len() {
// Collect neighbors' states dynamically
let neighbors: Vec<f64> = self
.agents
.iter()
.enumerate()
.filter(|&(j, _)| j != i) // Exclude the current agent
.map(|(_, agent)| agent.lock().unwrap().state)
.collect();
let agent = Arc::clone(&self.agents[i]);
thread::spawn(move || {
let mut agent = agent.lock().unwrap();
agent.update_state(&neighbors);
})
.join()
.unwrap(); // Ensure updates occur sequentially
}
}
/// Collect agent states for visualization
fn collect_states(&self) -> Vec<f64> {
self.agents
.iter()
.map(|agent| agent.lock().unwrap().state)
.collect()
}
/// Collect agent actions for visualization
fn collect_actions(&self) -> Vec<f64> {
self.agents
.iter()
.map(|agent| agent.lock().unwrap().action)
.collect()
}
}
/// Visualization of the agents' states and actions
fn visualize(states: &[f64], actions: &[f64], step: usize) {
let file_name = format!("step_{}.png", step); // File for the current step
let root = BitMapBackend::new(&file_name, (800, 600)).into_drawing_area();
root.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root)
.caption(format!("Agent States and Actions at Step {}", step), ("sans-serif", 30))
.x_label_area_size(30)
.y_label_area_size(30)
.build_cartesian_2d(0..states.len(), 0.0..2.0)
.unwrap();
chart.configure_mesh().draw().unwrap();
// Plot states
chart
.draw_series(states.iter().enumerate().map(|(i, &s)| {
Circle::new((i, s), 5, ShapeStyle::from(&BLUE).filled())
}))
.unwrap()
.label("States")
.legend(|(x, y)| Circle::new((x, y), 5, ShapeStyle::from(&BLUE).filled()));
// Plot actions
chart
.draw_series(actions.iter().enumerate().map(|(i, &a)| {
Circle::new((i, a), 5, ShapeStyle::from(&RED).filled())
}))
.unwrap()
.label("Actions")
.legend(|(x, y)| Circle::new((x, y), 5, ShapeStyle::from(&RED).filled()));
chart.configure_series_labels().border_style(&BLACK).draw().unwrap();
}
fn main() {
let environment = Environment::new(10); // Initialize 10 agents
for step in 0..5 {
environment.step(); // Update the environment for each step
let states = environment.collect_states();
let actions = environment.collect_actions();
visualize(&states, &actions, step); // Visualize the states and actions
for agent in &environment.agents {
let agent = agent.lock().unwrap();
println!(
"Agent {}: State = {:.2}, Action = {:.2}",
agent.id, agent.state, agent.action
);
}
println!("---");
}
println!("Visualization saved as images for each step.");
}
At each simulation step, each agent updates its state by averaging the states of its neighbors, which reflects cooperation and local interaction. Based on its updated state, the agent computes an action as a proportional response, capturing how agents adapt their behavior to their surroundings. These updates occur concurrently using threads to simulate distributed systems, while the states and actions of all agents are visualized to reveal system dynamics over time. The system provides insights into the convergence of agent behaviors and the emergence of order through decentralized, self-organizing principles, a core concept in multi-agent reinforcement learning systems.
The challenges in Multi-Agent Systems, including sample inefficiency, scalability, and data sparsity, require innovative solutions leveraging advanced mathematical modeling, machine learning, and ethical considerations. Future directions, such as lifelong learning, meta-learning, and quantum computing, promise to revolutionize MAS capabilities. Practical implementations in Rust demonstrate how these systems can be prototyped and scaled, enabling MAS to address real-world problems with efficiency, adaptability, and ethical integrity. Rust’s concurrency and performance features make it an ideal choice for building the next generation of scalable MAS applications.
11.9. Conclusion
This chapter provided a deep dive into the multi-disciplinary domain of Multi-Agent Systems (MAS), blending rigorous mathematical models with practical programming techniques in Rust. It showcased how MAS frameworks enable intelligent agent interactions in cooperative, competitive, and mixed environments, highlighting their role in solving complex real-world problems. Through discussions on taxonomy, communication strategies, game theory, and advanced reinforcement learning algorithms, the chapter emphasized the adaptability and scalability of MAS across various domains. With practical examples ranging from resource allocation to adversarial training and a forward-looking exploration of trends like meta-learning and ethical AI, this chapter equips readers with the knowledge and tools to innovate in the rapidly evolving field of MAS.
11.9.1. Further Learning with GenAI
Let these prompts inspire you to explore the depths of Multi-Agent Systems, blending theory with practice to build robust, scalable, and intelligent multi-agent frameworks using Rust.
Explain the foundational principles of Multi-Agent Systems (MAS). How do MAS differ from single-agent systems, and what mathematical frameworks, such as Markov Games and Dec-POMDPs, underpin their functionality? Implement a basic MAS framework in Rust, demonstrating agent interactions and rewards.
Discuss the taxonomy of MAS. How are Cooperative, Competitive, and Mixed MAS classified, and what role do graph-based models play in representing agent relationships? Implement a graph-based MAS framework in Rust, simulating agent interactions in a weighted graph structure.
Explore communication protocols in MAS. What are explicit and implicit communication mechanisms, and how do they enable coordination among agents? Implement a decentralized communication protocol in Rust using
tokioand analyze its effectiveness in a cooperative task.Analyze the dynamics of coordination in MAS. What are the key algorithms for distributed consensus and task allocation, and how do they ensure scalability? Implement a coordination task in Rust, such as dynamic resource allocation, and evaluate its scalability.
Examine the application of game theory in MAS. How do concepts like Nash Equilibrium, Pareto Optimality, and Minimax strategies shape multi-agent interactions? Simulate classic games like Prisoner's Dilemma in Rust and analyze the emergent behaviors of agents.
Explore advanced reinforcement learning algorithms for MAS. How do algorithms like MADDPG, QMIX, and MAAC extend classical RL to multi-agent contexts? Implement one of these algorithms in Rust and evaluate its performance in a simulated environment.
Discuss the challenges of non-stationarity in MAS. How does the evolving behavior of agents affect learning stability, and what techniques can mitigate this issue? Implement experience replay in Rust to address non-stationarity and analyze its impact.
Examine learning in cooperative MAS. What are the key techniques for joint policy learning and value decomposition? Implement a cooperative multi-agent task in Rust and measure the performance of different learning strategies.
Analyze adversarial learning in competitive MAS. How do self-play and minimax strategies enable agents to learn competitive behaviors? Implement a competitive MAS in Rust and evaluate the robustness of agents’ strategies.
Explore emergent behaviors in MAS. How do interactions among simple agents lead to complex, adaptive behaviors? Simulate emergent behavior in Rust, such as flocking in a swarm robotics scenario.
Discuss the application of MAS in real-world systems. How are MAS used in domains like swarm robotics, traffic management, and financial markets? Implement a traffic management MAS in Rust, optimizing for minimal congestion.
Examine scalability challenges in MAS. What techniques can be employed to manage large-scale systems, and how can Rust's performance features be leveraged? Implement a large-scale MAS simulation in Rust and analyze its efficiency.
Analyze the role of hierarchical structures in MAS. How do leader-follower models and multi-level optimization improve system performance? Implement a hierarchical MAS in Rust, demonstrating coordinated behaviors at multiple levels.
Discuss the trade-offs between centralized and decentralized learning in MAS. How do these approaches impact scalability, flexibility, and robustness? Implement both centralized and decentralized MAS frameworks in Rust and compare their outcomes.
Explore the integration of MAS with IoT and edge computing. How can MAS enhance distributed systems in IoT environments? Implement an edge-based MAS in Rust, simulating device collaboration for resource optimization.
Examine the role of ethical considerations in MAS deployment. What challenges arise from deploying MAS in critical applications, and how can fairness and transparency be ensured? Implement safeguards in a Rust-based MAS to address ethical concerns.
Discuss the application of MAS in autonomous systems. How do MAS contribute to areas like autonomous vehicles, drones, and smart factories? Implement a MAS for drone swarm optimization in Rust and evaluate its effectiveness.
Analyze the use of reward shaping in MAS. How does modifying reward functions influence learning and cooperation? Implement reward shaping techniques in Rust and observe their effects on agent behaviors in a cooperative task.
Explore the future directions of MAS research. What emerging trends, such as meta-learning, communication-free MAS, and lifelong learning, are shaping the field? Implement a meta-learning-based MAS in Rust and test its adaptability to dynamic environments.
Examine the use of transfer learning in MAS. How can knowledge from one MAS be transferred to another to accelerate learning? Implement transfer learning techniques in Rust for a multi-agent setup and evaluate their efficiency.
These prompts are designed to guide you through the theoretical underpinnings, architectural designs, and practical implementations of MAS. Use them to deepen your understanding and master the art of building intelligent, collaborative systems using Rust.
11.9.2. Hands On Practices
These exercises encourage hands-on experimentation and critical engagement with MAS concepts, allowing readers to apply their knowledge practically and explore real-world scenarios.
Exercise 11.1: Building a Basic Multi-Agent System Framework
Task:
Create a basic MAS framework in Rust that simulates agents interacting in a grid environment. Implement both homogeneous and heterogeneous agents with distinct policies and goals.
Challenge:
Experiment with different reward structures (e.g., shared rewards vs. independent rewards) and analyze their impact on agent behavior and overall system performance. Visualize agent interactions using the plotters crate to observe emergent dynamics.
Exercise 11.2: Communication and Coordination in MAS
Task:
Implement a decentralized communication protocol in Rust using tokio, enabling agents to share information about their states and goals in a cooperative environment.
Challenge:
Simulate a coordinated task, such as resource sharing or collaborative navigation. Experiment with different communication strategies (e.g., explicit vs. implicit) and measure their impact on the agents' ability to complete the task efficiently.
Exercise 11.3: Simulating Strategic Interactions Using Game Theory
Task:
Implement a multi-agent scenario in Rust based on game-theoretic principles, such as the Prisoner's Dilemma or a Stag Hunt game. Use Rust’s ndarray crate to model payoff matrices and strategies.
Challenge:
Analyze the behavior of agents under different strategies (e.g., tit-for-tat, random, or always cooperate). Extend the implementation to include repeated games and explore the emergence of cooperative or competitive equilibria over time.
Exercise 11.4: Implementing Multi-Agent Reinforcement Learning Algorithms
Task:
Develop a multi-agent Q-learning or policy gradient algorithm in Rust for a simple shared environment, such as navigation or resource collection. Use the tch crate for neural network-based agents.
Challenge:
Experiment with centralized vs. decentralized training methods. Compare their learning efficiency, stability, and scalability in the context of non-stationary agent behaviors.
Exercise 11.5: Modeling Emergent Behaviors in a Swarm System
Task:
Simulate a swarm robotics system in Rust where simple agents interact to achieve collective goals, such as flocking or object transport. Implement rules like alignment, separation, and cohesion for the agents.
Challenge:
Analyze the impact of adjusting agent interaction parameters (e.g., communication radius, obstacle avoidance) on the emergence of swarm behaviors. Experiment with adding leader agents and observe their influence on the swarm's overall efficiency and adaptability.
By implementing these exercises, you will develop a deeper understanding of the challenges and opportunities in MAS, explore how multi-agent dynamics emerge from simple rules, and enhance your proficiency in using Rust to build scalable and efficient MAS solutions.
Comments