12.1. Game Theory in MARL link

Game theory has long been a cornerstone for understanding and predicting interactions among rational agents in strategic environments. Emerging from the fields of economics and mathematics in the early 20th century, it was initially developed to analyze competitive and cooperative behaviors in settings involving multiple decision-makers. Foundational contributions by John von Neumann and Oskar Morgenstern in their seminal 1944 work, Theory of Games and Economic Behavior, formalized the study of strategic interactions, introducing concepts such as zero-sum games and equilibrium strategies. These ideas provided a rigorous framework for studying conflicts, negotiations, and collaborations in systems where agents act both independently and interdependently.

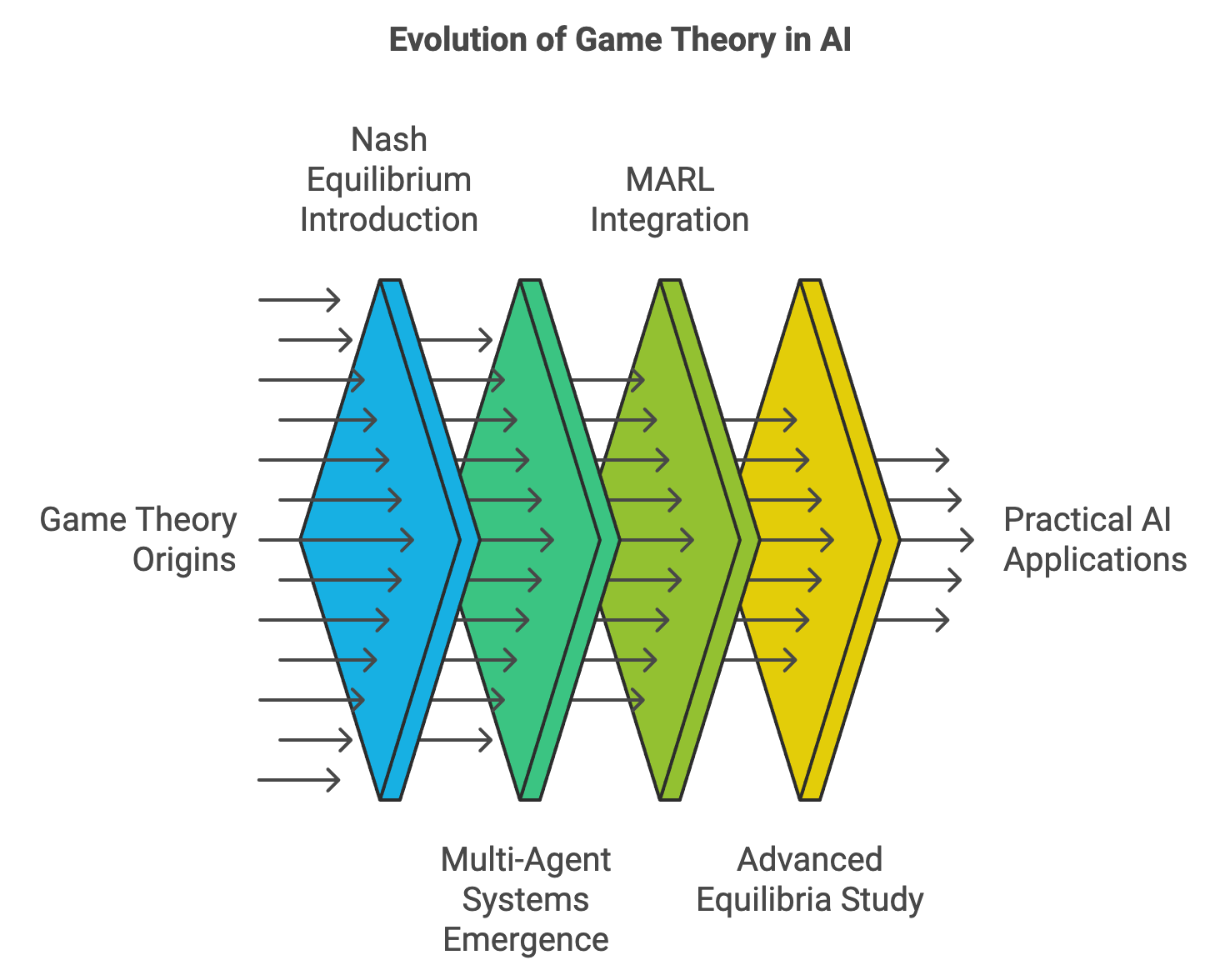
Figure 1: The evolution of Game Theory in AI.

John Nash's groundbreaking work in the 1950s extended the framework with the concept of Nash equilibrium, which describes a state where no agent can improve their outcome by unilaterally changing their strategy. This theoretical insight was a major step in understanding how rational agents might behave in non-cooperative settings, laying the foundation for analyzing complex multi-agent dynamics. These early contributions emphasized the importance of balancing individual incentives with collective outcomes, a theme that continues to resonate in modern applications of game theory.

In the context of artificial intelligence (AI) and machine learning, the relevance of game theory grew as researchers began addressing problems involving multiple autonomous entities. Early AI systems focused largely on single-agent scenarios, where the environment was static and unaffected by the agent's actions. However, as multi-agent systems (MAS) emerged—spanning domains such as robotics, economics, and distributed computing—the need for frameworks that could model interactions among agents became clear. Game theory provided a natural fit, offering tools to formalize and analyze the strategic behavior of agents operating within shared environments.

The integration of game theory into Multi-Agent Reinforcement Learning (MARL) marked a significant evolution. Traditional reinforcement learning (RL) methods, while effective for single-agent environments, struggled in multi-agent settings due to the inherent non-stationarity of such systems. In MARL, the environment continually evolves as agents adapt their strategies, creating dynamic and often adversarial conditions. Game theory addressed this challenge by providing a theoretical basis for modeling strategic interactions, enabling the design of algorithms that account for both cooperation and competition.

The motivation for combining game theory with MARL stems from its applicability to real-world problems involving multiple interacting entities. Consider autonomous driving, where vehicles must navigate a shared roadway, balancing cooperative behaviors (e.g., merging lanes safely) with competitive goals (e.g., minimizing travel time). Similarly, in financial markets, trading agents compete to maximize profits while adhering to market dynamics that depend on collective behaviors. In robotics, multi-agent teams collaborate to perform tasks like search-and-rescue or warehouse automation, requiring coordination and conflict resolution.

Modern MARL systems leverage game-theoretic principles to address challenges such as equilibrium computation, credit assignment, and strategy adaptation. For example, algorithms like Multi-Agent Deep Deterministic Policy Gradient (MADDPG) and QMIX incorporate elements of game theory to optimize agent policies in cooperative and mixed environments. These algorithms extend traditional RL by considering the interactions between agents, enabling them to learn behaviors that are robust to the actions of others.

Game theory's role in MARL also encompasses the study of equilibria beyond Nash equilibrium, such as Bayesian equilibrium for scenarios with incomplete information and Stackelberg equilibrium for hierarchical decision-making. These advanced concepts are critical for designing systems where agents must operate under uncertainty or within structured hierarchies, as seen in applications like supply chain optimization and military strategy.

This section delves into the advanced theoretical foundations of game theory in MARL, elucidates its integration into MARL architectures, and demonstrates its practical implementation using Rust. By exploring these ideas, we highlight how game theory enables agents to navigate the complexities of multi-agent environments, fostering cooperation, competition, and strategic adaptability. Through Rust-based implementations, readers will gain practical insights into how these principles can be translated into robust and scalable systems for real-world applications. The historical evolution of game theory in MARL underscores its enduring relevance and potential to address the challenges of increasingly interconnected and dynamic systems.

Game theory defines a strategic interaction, or game, as a formal structure $G = (N, A, U)$, where $N$ is the set of agents, $A = A_1 \times A_2 \times \cdots \times A_n$ represents the joint action space, and $U = \{u_1, u_2, \dots, u_n\}$ denotes the utility functions associated with each agent. These utility functions govern the rewards agents seek to maximize.

For MARL, this formalism extends to dynamic environments, where agents' strategies and rewards evolve based on their learning processes. For example, in stochastic games, the state of the environment transitions based on joint actions, described by the probability function $P(s' \mid s, a)$, where $s$ is the current state, $s'$ is the next state, and $a$ is the joint action. Each agent seeks to maximize its cumulative discounted reward:

$$ R_i = \mathbb{E}\left[\sum_{t=0}^\infty \gamma^t u_i(s_t, a_t)\right], $$

where $\gamma$ is the discount factor that controls the agent's preference for immediate versus future rewards.

Bayesian games introduce another layer of complexity, modeling scenarios where agents have incomplete information. Each agent $i$ is characterized by a type $\theta_i$, drawn from a distribution $P(\Theta)$. The agents adopt strategies $\pi_i(\theta_i)$ that maximize expected utilities given their beliefs:

$$ \pi_i^*(\theta_i) = \arg\max_{\pi_i} \mathbb{E}[u_i(a_i, a_{-i}, \theta) \mid \theta_i]. $$

These models allow MARL systems to simulate uncertainty and incomplete information, critical in many real-world applications.

Reward shaping in MARL uses potential-based functions to align individual agent rewards with desired system-wide outcomes. A modified utility function takes the form:

$$ u_i'(s, a, s') = u_i(s, a, s') + \Phi(s, s'), $$

where $\Phi(s, s')$ is the shaping potential. This mechanism accelerates learning by guiding agents toward cooperative or efficient behaviors without altering equilibria.

The integration of game theory into MARL provides a powerful framework for modeling and analyzing agent interactions. Agents in MARL environments engage in static, dynamic, or repeated games, each presenting unique challenges and opportunities.

Static games involve one-shot interactions where agents simultaneously choose actions. These games are represented by payoff matrices and analyzed to identify Nash equilibria, where no agent can improve its utility by unilaterally changing its strategy. However, many real-world scenarios involve repeated interactions, where agents update strategies based on prior outcomes. In these dynamic and repeated games, equilibrium concepts extend to strategies over time, such as subgame-perfect equilibria.

In MARL, agents often operate in environments requiring real-time adaptation. Game-theoretic reasoning provides a formalism for designing adaptive strategies that respond to other agents' actions dynamically. The use of equilibrium concepts like Nash equilibria and Pareto optimality enables MARL systems to stabilize behaviors and optimize outcomes.

By embedding these principles into MARL architectures, agents can leverage strategies informed by game theory to make decisions that account for both individual and collective objectives. For example, policies in MARL can incorporate mechanisms for equilibrium learning, allowing agents to converge to stable strategies over time.

The following Rust program combines game-theoretic concepts, simulations of repeated and stochastic games, and visualization of results into a single cohesive implementation. This code implements a Multi-Agent Reinforcement Learning (MARL) simulation where two agents interact repeatedly in a normal-form game. The agents dynamically adapt their mixed strategies using a form of fictitious play, where each agent adjusts its probability distribution over actions based on the payoffs received in previous rounds. The model incorporates key game-theoretic concepts, including strategy evolution and cumulative payoffs, to demonstrate how agents adapt and converge to equilibria over repeated interactions.

use ndarray::Array2;
use rand::Rng;
use plotters::prelude::*;

/// Represents a normal-form game with payoff matrices for two agents.
struct NormalFormGame {
    payoff_matrix: Array2<f64>,
}

impl NormalFormGame {
    fn new(matrix: Array2<f64>) -> Self {
        Self { payoff_matrix: matrix }
    }

    /// Computes the expected utility for Player 1 given their mixed strategy.
    fn compute_expected_utility(&self, strategy_p1: &[f64], strategy_p2: &[f64]) -> f64 {
        let mut expected_utility = 0.0;
        for i in 0..strategy_p1.len() {
            for j in 0..strategy_p2.len() {
                expected_utility += strategy_p1[i] * strategy_p2[j] * self.payoff_matrix[[i, j]];
            }
        }
        expected_utility
    }
}

/// Simulates a repeated game for two agents with random strategies.
fn simulate_repeated_game(rounds: usize) -> (Vec<f64>, Vec<f64>) {
    let mut rng = rand::thread_rng();
    let mut cumulative_score_p1 = 0.0;
    let mut cumulative_score_p2 = 0.0;
    let mut scores_p1 = vec![];
    let mut scores_p2 = vec![];

    for _ in 0..rounds {
        let action_p1 = rng.gen_range(0..2);
        let action_p2 = rng.gen_range(0..2);

        // Example payoff matrix for a repeated game
        let payoff = match (action_p1, action_p2) {
            (0, 0) => (3.0, 3.0), // Both cooperate
            (0, 1) => (0.0, 5.0), // Player 1 defects
            (1, 0) => (5.0, 0.0), // Player 2 defects
            (1, 1) => (1.0, 1.0), // Both defect
            _ => (0.0, 0.0),
        };

        cumulative_score_p1 += payoff.0;
        cumulative_score_p2 += payoff.1;

        scores_p1.push(cumulative_score_p1);
        scores_p2.push(cumulative_score_p2);
    }

    (scores_p1, scores_p2)
}

/// Plots the payoff evolution over time.
fn plot_payoff_evolution(scores: (Vec<f64>, Vec<f64>), filename: &str) -> Result<(), Box<dyn std::error::Error>> {
    let root = BitMapBackend::new(filename, (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .caption("Payoff Evolution", ("sans-serif", 20))
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..scores.0.len(), 0.0..*scores.0.iter().chain(scores.1.iter()).fold(0.0 / 0.0, f64::max))?;

    chart.configure_mesh().draw()?;

    chart.draw_series(LineSeries::new(
        scores.0.iter().enumerate().map(|(x, &y)| (x, y)),
        &BLUE,
    ))?.label("Player 1").legend(|(x, y)| PathElement::new([(x, y), (x + 10, y)], &BLUE));

    chart.draw_series(LineSeries::new(
        scores.1.iter().enumerate().map(|(x, &y)| (x, y)),
        &RED,
    ))?.label("Player 2").legend(|(x, y)| PathElement::new([(x, y), (x + 10, y)], &RED));

    chart.configure_series_labels().background_style(&WHITE.mix(0.8)).border_style(&BLACK).draw()?;

    Ok(())
}

fn main() -> Result<(), Box<dyn std::error::Error>> {
    // Define a normal-form game payoff matrix
    let payoff_matrix = Array2::from_shape_vec((2, 2), vec![3.0, 0.0, 5.0, 1.0]).unwrap();
    let game = NormalFormGame::new(payoff_matrix);

    // Compute expected utility
    let strategy_p1 = vec![0.5, 0.5];
    let strategy_p2 = vec![0.4, 0.6];
    let expected_utility = game.compute_expected_utility(&strategy_p1, &strategy_p2);
    println!("Expected Utility for Player 1: {:.2}", expected_utility);

    // Simulate repeated game
    let rounds = 100;
    let scores = simulate_repeated_game(rounds);

    // Plot payoff evolution
    plot_payoff_evolution(scores, "payoff_evolution.png")?;

    Ok(())
}

The simulation starts with a predefined payoff matrix for the two agents and initializes their strategies with uniform probabilities. During each round, both agents select actions stochastically based on their current strategies. The payoffs are determined using the normal-form game's payoff matrix, and the agents update their strategies by assigning higher probabilities to actions that yielded higher payoffs. This iterative process simulates learning dynamics, allowing the agents to refine their strategies over time based on past interactions. The simulation tracks the cumulative payoffs and strategy evolution of the agents over a specified number of rounds.

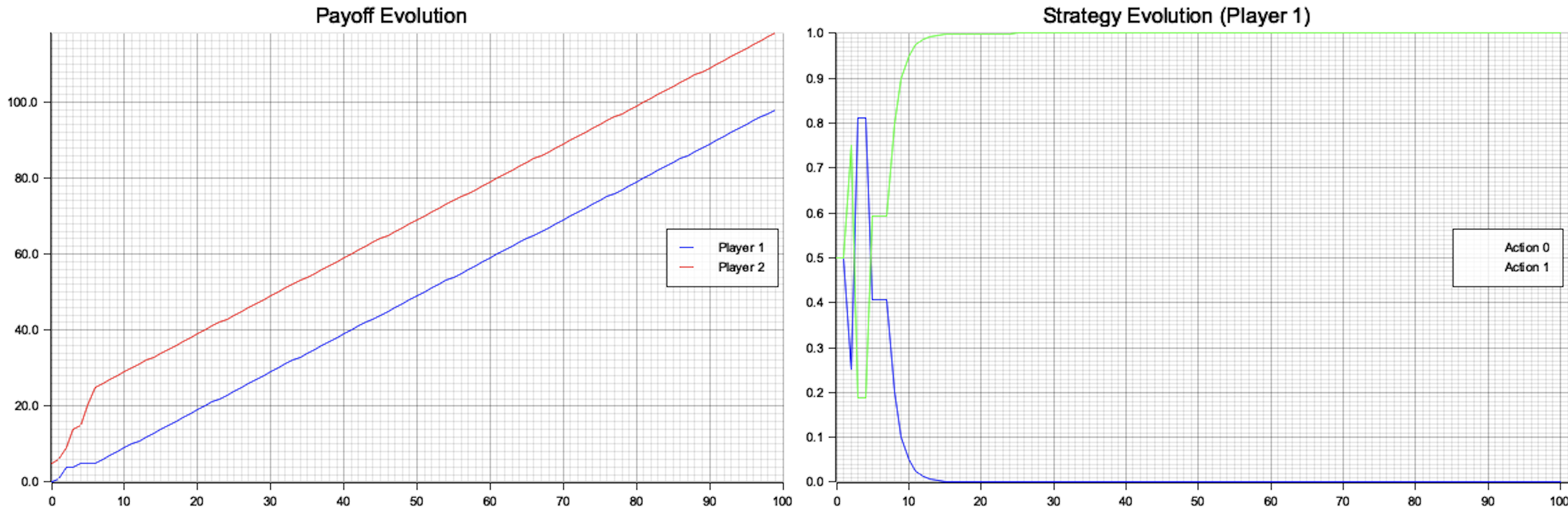
Figure 2: Plotters visualization of payoff and strategy evolutions.

The visualization consists of two plots. The left plot shows the cumulative payoffs for Player 1 (blue) and Player 2 (red) over the course of the simulation. It indicates how each player's rewards accumulate, reflecting the interplay of strategies and actions. The right plot depicts the evolution of Player 1's strategy over time, showing the probabilities assigned to each action (Action 0 in blue and Action 1 in green). Initially, both actions are played with nearly equal probabilities, but over time, the probabilities converge, reflecting the learning dynamics and strategy adaptation. Together, the plots demonstrate how agents adapt to maximize their payoffs and approach an equilibrium state.

12.2. Cooperative Game Theory for MARL link

Cooperative game theory serves as a robust framework for fostering collaboration in Multi-Agent Systems (MAS), enabling agents to align their efforts toward achieving shared objectives. Unlike non-cooperative scenarios, where agents prioritize individual payoffs, cooperative game theory emphasizes collective optimization and equitable distribution of rewards. This paradigm is particularly valuable in Multi-Agent Reinforcement Learning (MARL), where the dynamics of interaction involve agents working together, even in competitive or resource-constrained environments. By leveraging principles such as coalitions, transferable utility, and fairness, cooperative game theory provides a structured approach to designing mechanisms that incentivize and sustain collaboration among agents.

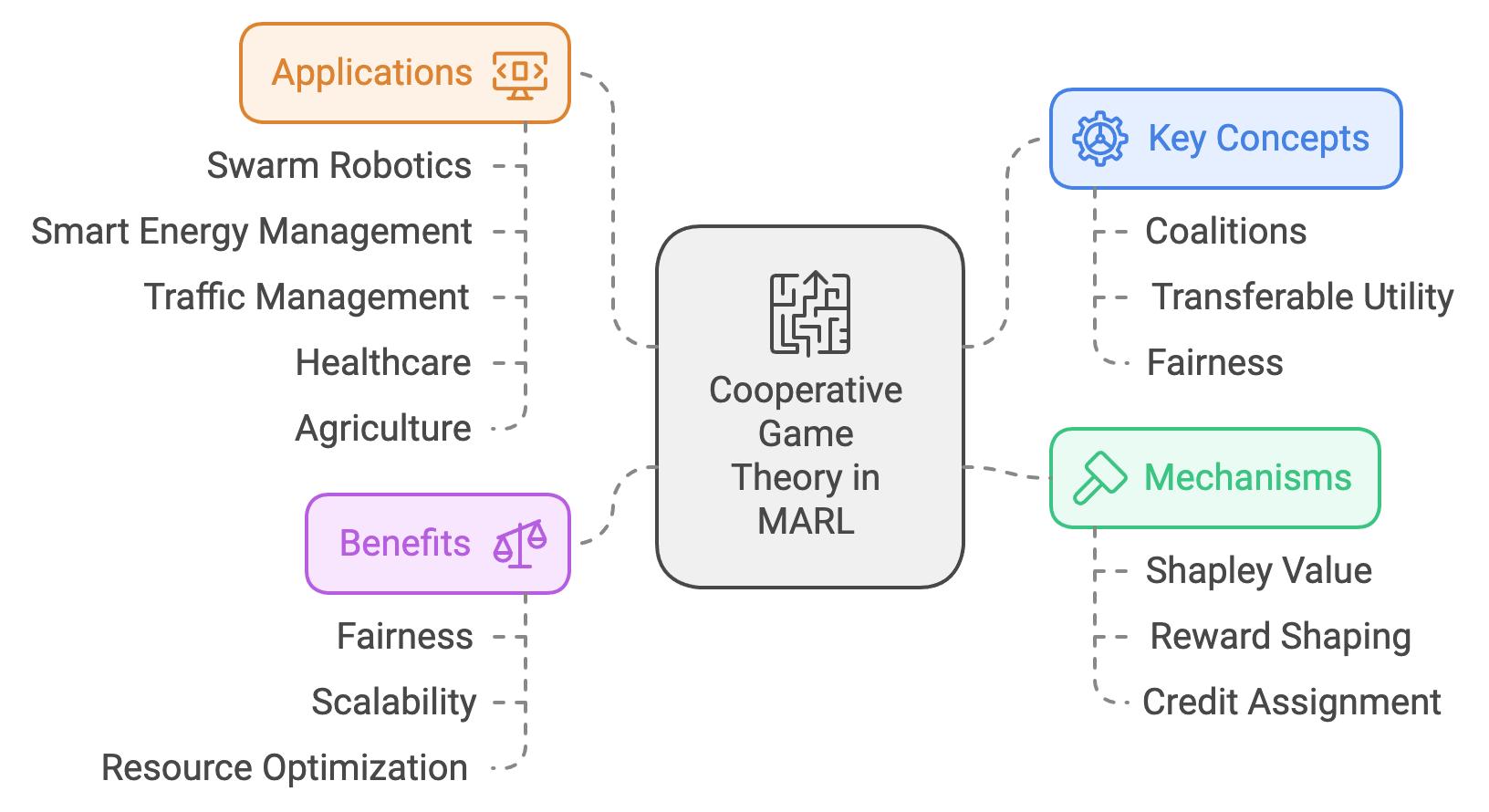
Figure 3: Scopes of cooperative games theory in RL.

The theoretical foundation of cooperative game theory in MARL is built on the concept of forming coalitions, where subsets of agents combine resources and expertise to accomplish tasks more effectively than they could independently. The value of a coalition reflects the collective payoff achievable through collaboration, and mechanisms such as the Shapley value ensure fair reward distribution based on individual contributions. These mechanisms are essential in preventing conflicts and encouraging agents to maintain long-term cooperation. In MARL, these ideas are implemented through techniques like reward shaping, where agents are guided to align their actions with global objectives, and credit assignment, which ensures equitable reward distribution in cooperative tasks. Such approaches help resolve challenges where individual incentives might otherwise conflict with collective goals.

Conceptually, integrating cooperative game theory into MARL enables the modeling of interactions that balance individual autonomy with the efficiency of collective action. This integration is particularly important in environments where agents face trade-offs between self-interest and shared benefits. For instance, in a smart grid, individual households may need to adjust their energy consumption during peak hours to prevent blackouts, sacrificing immediate utility for system stability. Cooperative MARL ensures that agents make such trade-offs effectively, optimizing the system's overall performance while preserving fairness among participants. Similarly, in logistics and supply chain management, cooperative strategies help align the goals of suppliers, manufacturers, and distributors, ensuring that resources are allocated efficiently and equitably across the network.

The applications of cooperative MARL span numerous domains. In swarm robotics, for example, groups of drones or autonomous robots collaborate on tasks such as search-and-rescue operations or surveillance missions. Cooperative game theory ensures that these agents distribute tasks efficiently, maximizing coverage and minimizing resource consumption. In smart energy management, agents representing households, businesses, and power plants work together to balance energy supply and demand, integrating renewable sources while reducing costs and maintaining system reliability. Similarly, in traffic management, autonomous vehicles use cooperative strategies to coordinate their movements, optimizing traffic flow, reducing congestion, and improving fuel efficiency. These systems benefit from cooperative MARL by aligning individual vehicle goals with the broader objectives of safety and efficiency.

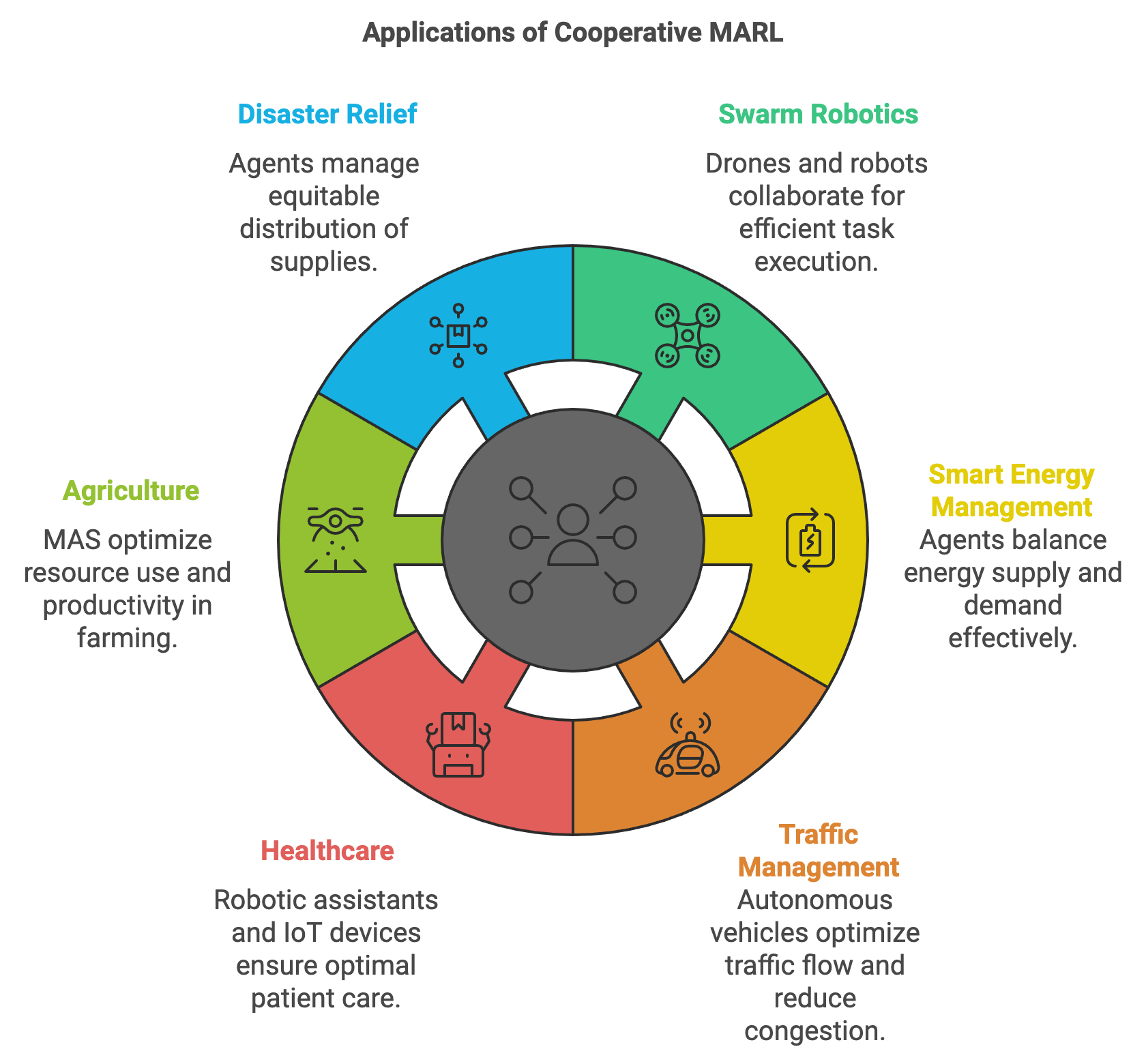
Figure 4: Use cases and applications of Cooperative MARL.

Other domains, such as healthcare, also benefit significantly from cooperative MARL. In hospitals, robotic assistants and IoT devices coordinate tasks like patient monitoring, medication delivery, and surgery assistance. Cooperative strategies enable these systems to dynamically allocate resources and responsibilities, ensuring optimal care for patients. In agriculture, MAS-powered precision farming systems deploy drones and ground robots to monitor crop health, irrigate fields, and perform pest control. These agents collaborate to optimize resource use while ensuring uniform productivity across large farms. Similarly, in disaster relief operations, MAS agents manage the distribution of essential supplies like food and medicine, ensuring equitable allocation based on urgency and population density.

The value of cooperative game theory in MARL extends beyond practical applications to addressing fundamental challenges of fairness, scalability, and resource optimization. By enabling agents to form and sustain productive partnerships, cooperative MARL ensures that systems remain robust and adaptable, even in dynamic and uncertain environments. It provides a framework for balancing individual and collective incentives, ensuring that agents contribute equitably to shared objectives while achieving their personal goals. This balance is critical for building systems that not only solve complex real-world problems but also foster trust, collaboration, and long-term efficiency.

Through the integration of cooperative game theory, MARL achieves a level of adaptability and robustness essential for real-world applications. By emphasizing shared objectives, fairness, and equitable resource allocation, this paradigm unlocks the potential of MAS to address challenges across domains such as energy, healthcare, transportation, and agriculture. As MAS continue to evolve, cooperative game theory will remain a cornerstone of their development, providing the theoretical and practical tools needed to build intelligent, scalable, and ethically responsible systems.

In cooperative game theory, the fundamental structure is a coalitional game represented as $(N, v)$, where:

• $N = \{1, 2, \dots, n\}$ is the set of agents.

• $v: 2^N \to \mathbb{R}$ is the characteristic function assigning a value $v(S)$ to each coalition $S \subseteq N$, representing the utility achievable by that coalition.

A coalition $S$ achieves stability if no subset of agents $T \subseteq S$ can achieve a higher value $v(T)$ independently. Stability is captured mathematically through the core of the game:

$$ \text{Core}(v) = \{x \in \mathbb{R}^n : \sum_{i \in N} x_i = v(N), \, \sum_{i \in S} x_i \geq v(S), \forall S \subseteq N\}, $$

where $x_i$ is the payoff assigned to agent $i$.

Graph theory enhances cooperative frameworks by modeling agents as nodes in a graph $G = (N, E)$, where edges $E$ represent potential collaborations. Weighting the edges by shared utilities $u(i, j)$ allows for structured coalition formation.

Metrics like the Banzhaf Power Index and Shapley values measure individual agents’ contributions to coalitions. The Shapley value for agent $i$ is given by:

$$ \phi_i(v) = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|! (|N| - |S| - 1)!}{|N|!} \big[v(S \cup \{i\}) - v(S)\big]. $$

This provides a principled approach to reward redistribution, ensuring fairness and incentivizing cooperation.

Reward shaping can further incentivize cooperative behavior by modifying utility functions:

$$ u'_i(s, a, s') = u_i(s, a, s') + \alpha \sum_{j \neq i} u_j(s, a, s'), $$

where $\alpha$ balances individual and collective rewards. This fosters cooperation even in competitive settings.

Modern MARL techniques leverage cooperative game theory for joint utility maximization and robust policy optimization. Agents optimize shared objectives through cooperative policy optimization, which extends traditional policy gradient methods to maximize a global reward:

$$ J(\pi) = \mathbb{E}\left[\sum_{t=0}^\infty \gamma^t \sum_{i \in N} u_i(s_t, a_t)\right]. $$

In decentralized systems, communication frameworks enable agents to coordinate actions effectively. Message-passing architectures, where agents exchange partial observations or intentions, enhance coordination. For instance, graph neural networks (GNNs) can process these interactions to optimize joint policies.

Cooperative MARL finds applications in real-world scenarios like climate modeling, where agents represent stakeholders mitigating environmental impacts, or shared resource management, where agents allocate limited resources efficiently.

This Rust program models a cooperative multi-agent reinforcement learning (MARL) environment using graph-based coalition modeling. It calculates and visualizes Shapley values to fairly redistribute rewards among agents in a coalition game. Shapley values are derived from cooperative game theory and represent each agent's contribution to the coalition's success. The implementation uses BTreeSet for consistent coalition handling, HashMap for value storage, and the plotters crate to visualize the results.

use std::collections::{BTreeSet, HashMap};
use plotters::prelude::*;

/// Represents a coalition game with a characteristic function.
struct CoalitionGame {
    agents: BTreeSet<usize>,
    value_function: HashMap<BTreeSet<usize>, f64>,
}

impl CoalitionGame {
    fn new(agents: BTreeSet<usize>, value_function: HashMap<BTreeSet<usize>, f64>) -> Self {
        Self { agents, value_function }
    }

    /// Computes the Shapley value for each agent in the game.
    fn compute_shapley_values(&self) -> HashMap<usize, f64> {
        let mut shapley_values = HashMap::new();
        let n = self.agents.len() as f64;

        for &agent in &self.agents {
            let mut shapley_value = 0.0;

            for subset in self.power_set_except(&agent) {
                let mut subset_with_agent = subset.clone();
                subset_with_agent.insert(agent);
                let marginal_contribution =
                    self.value_of(&subset_with_agent) - self.value_of(&subset);
                shapley_value += marginal_contribution / ((subset.len() + 1) as f64 * n);
            }
            shapley_values.insert(agent, shapley_value);
        }

        shapley_values
    }

    /// Computes the value of a given coalition.
    fn value_of(&self, coalition: &BTreeSet<usize>) -> f64 {
        *self.value_function.get(coalition).unwrap_or(&0.0)
    }

    /// Generates the power set of agents, excluding a specific agent.
    fn power_set_except(&self, exclude: &usize) -> Vec<BTreeSet<usize>> {
        let mut subsets = vec![BTreeSet::new()];
        for &agent in &self.agents {
            if agent != *exclude {
                let mut new_subsets = vec![];
                for subset in &subsets {
                    let mut new_subset = subset.clone();
                    new_subset.insert(agent);
                    new_subsets.push(new_subset);
                }
                subsets.extend(new_subsets);
            }
        }
        subsets
    }
}

/// Simulates a cooperative MARL environment with reward redistribution.
fn simulate_cooperative_marl() -> HashMap<usize, f64> {
    let agents: BTreeSet<usize> = (1..=3).collect();
    let mut value_function = HashMap::new();

    value_function.insert(BTreeSet::from([1]), 10.0);
    value_function.insert(BTreeSet::from([2]), 15.0);
    value_function.insert(BTreeSet::from([3]), 20.0);
    value_function.insert(BTreeSet::from([1, 2]), 40.0);
    value_function.insert(BTreeSet::from([1, 3]), 50.0);
    value_function.insert(BTreeSet::from([2, 3]), 60.0);
    value_function.insert(BTreeSet::from([1, 2, 3]), 100.0);

    let game = CoalitionGame::new(agents, value_function);
    let shapley_values = game.compute_shapley_values();
    println!("Shapley Values: {:?}", shapley_values);

    shapley_values
}

/// Visualizes coalition contributions using Shapley values.
fn visualize_shapley_values(
    shapley_values: &HashMap<usize, f64>,
) -> Result<(), Box<dyn std::error::Error>> {
    let root = BitMapBackend::new("shapley_values.png", (640, 480)).into_drawing_area();
    root.fill(&WHITE)?;

    let max_value = shapley_values.values().cloned().fold(0.0, f64::max);
    let mut chart = ChartBuilder::on(&root)
        .caption("Shapley Values", ("sans-serif", 20))
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..shapley_values.len(), 0.0..max_value)?;

    chart.configure_mesh().draw()?;

    chart.draw_series(
        shapley_values
            .iter()
            .enumerate()
            .map(|(idx, (&_agent, &value))| {
                Rectangle::new([(idx, 0.0), (idx + 1, value)], RED.filled())
            }),
    )?;

    Ok(())
}

fn main() -> Result<(), Box<dyn std::error::Error>> {
    let shapley_values = simulate_cooperative_marl();
    visualize_shapley_values(&shapley_values)?;
    println!("Shapley values have been saved to 'shapley_values.png'.");

    Ok(())
}

The program simulates a coalition game with agents, each contributing to various coalitions with specified value functions. The core functionality involves calculating Shapley values for all agents by iterating over coalitions and computing marginal contributions. The CoalitionGame struct handles coalition value retrieval and Shapley value computation. The simulate_cooperative_marl function defines the game environment, including agents and coalition values, while the visualize_shapley_values function generates a bar chart showing each agent’s Shapley value. The program outputs the computed values to the console and saves the visualization as an image, providing insights into agent contributions and reward distribution in cooperative settings.

Cooperative game theory is a powerful tool for fostering collaboration among agents in MARL. By integrating concepts like coalition formation, fairness metrics, and reward redistribution, agents can achieve robust cooperation even in complex environments. The Rust implementation provided demonstrates how these theoretical ideas can be realized in practical systems, enabling the development of scalable, cooperative multi-agent architectures.

12.3. Non-Cooperative Game Theory in MARL link

Non-cooperative game theory serves as an essential framework for understanding competitive interactions where agents prioritize individual rewards without assuming any cooperation. This approach is particularly relevant in Multi-Agent Reinforcement Learning (MARL), where agents often operate in environments characterized by conflicting goals, adversarial dynamics, or resource scarcity. The foundational principles of non-cooperative game theory, such as Nash equilibrium and zero-sum games, provide the mathematical basis for analyzing and designing agent strategies in these complex settings. By integrating these principles into MARL, researchers and practitioners can develop systems that are robust, adaptive, and capable of navigating competitive and self-interested environments.

One of the most prominent applications of non-cooperative game theory in MARL is autonomous traffic management. In this domain, individual vehicles (agents) act in their self-interest to minimize travel time, fuel consumption, or cost. However, the actions of each vehicle affect the overall traffic flow, creating a dynamic, competitive environment. Non-cooperative MARL algorithms enable vehicles to learn optimal driving strategies while anticipating the behaviors of other drivers. For instance, in scenarios involving lane merging or intersection management, vehicles must balance assertiveness with caution to achieve their objectives without causing collisions or significant delays for others. Non-cooperative frameworks allow vehicles to model and adapt to the competitive strategies of other agents, ensuring safety and efficiency even in densely populated traffic systems.

Figure 5: Scopes of non-cooperative game theory in MARL.

In financial markets, non-cooperative game theory underpins the design of trading algorithms that operate in competitive environments. Here, agents represent traders, each seeking to maximize their profits through buying, selling, and arbitrage. The strategies of one agent influence market dynamics, affecting the outcomes for others. Non-cooperative MARL enables these agents to adapt to market trends and counteract the strategies of competitors, such as detecting and responding to price manipulation or identifying optimal entry and exit points. This application is particularly critical in high-frequency trading, where decisions must be made in fractions of a second based on continuously changing market conditions. By leveraging the principles of non-cooperative game theory, MARL algorithms ensure that trading agents can remain competitive and resilient in volatile markets.

Cybersecurity is another domain where non-cooperative game theory plays a critical role. In this context, agents often represent attackers and defenders in an adversarial environment. Attackers aim to exploit vulnerabilities in systems, while defenders seek to prevent breaches and mitigate damage. Non-cooperative MARL models these interactions, allowing defenders to anticipate and counteract potential threats effectively. For example, in a network security scenario, a defender agent might learn to detect anomalous behaviors indicative of an attack, such as unusual data access patterns or unauthorized network activity. Simultaneously, attacker agents adapt their strategies to evade detection, creating a dynamic and evolving competition. This framework enhances the robustness of cybersecurity systems by enabling continuous learning and adaptation to emerging threats.

The principles of non-cooperative game theory also extend to resource allocation in competitive environments, such as telecommunications networks. In these systems, agents represent users or devices competing for limited bandwidth or computational resources. Non-cooperative MARL allows agents to optimize their resource usage while minimizing interference with others, ensuring efficient and equitable distribution. For instance, in a cellular network, devices might learn to adjust their transmission power or frequency to maximize data throughput without causing excessive congestion or interference. This approach improves the overall performance and reliability of the network, particularly in high-demand scenarios.

In robotics, non-cooperative MARL facilitates the development of systems that operate in competitive or adversarial settings, such as robot soccer or drone racing. In robot soccer, agents must balance offensive and defensive strategies to outmaneuver opponents and score goals, all while adapting to the dynamic movements of other players. Similarly, in drone racing, each agent competes to navigate a course as quickly as possible while avoiding collisions and maintaining optimal flight paths. Non-cooperative MARL algorithms enable these robots to learn strategies that optimize their performance in the presence of competitors, making them more effective and adaptive in real-world applications.

Non-cooperative game theory also finds applications in negotiation and auction systems, where agents act as self-interested participants competing for resources or agreements. In automated negotiations, agents represent parties with conflicting objectives, such as buyers and sellers, seeking to maximize their respective utilities. Non-cooperative MARL allows these agents to model and predict the strategies of others, enabling them to make optimal offers and counteroffers. Similarly, in auction systems, agents learn bidding strategies that maximize their chances of winning while minimizing costs. These applications are particularly relevant in e-commerce, supply chain management, and public resource allocation.

The integration of non-cooperative game theory into MARL provides a structured approach for modeling and solving competitive multi-agent problems. By leveraging Rust’s high-performance capabilities, practical implementations of these systems can be both scalable and reliable. For example, Rust's concurrency model and memory safety features ensure that MARL simulations involving hundreds or thousands of agents operate efficiently and without errors. These implementations allow researchers and practitioners to explore complex competitive dynamics in environments such as autonomous traffic systems, financial markets, and cybersecurity, bridging the gap between theoretical insights and real-world applications.

In summary, non-cooperative game theory in MARL enables the development of systems that navigate competitive and adversarial environments with strategic precision. Applications in domains like autonomous vehicles, financial markets, cybersecurity, telecommunications, robotics, and negotiation systems demonstrate the versatility and importance of this framework. By combining robust theoretical principles with cutting-edge MARL algorithms and Rust-based implementations, these systems are equipped to address some of the most challenging problems in modern multi-agent interactions, ensuring adaptability, resilience, and optimal performance in diverse competitive settings.

Non-cooperative games are formally defined by the tuple $G = (N, A, U)$, where $N$ is the set of agents, $A = A_1 \times A_2 \times \cdots \times A_n$ represents the joint action space, and $U = \{u_1, u_2, \dots, u_n\}$ are the utility functions associated with each agent. Each agent $i \in N$ seeks to maximize their individual utility $u_i(a)$, where $a = (a_1, a_2, \dots, a_n) \in A$.

The Nash Equilibrium is a critical concept where no agent can unilaterally improve their utility by deviating from their current strategy. Mathematically, a strategy profile $\pi = (\pi_1, \pi_2, \dots, \pi_n)$ is a Nash Equilibrium if:

$$ u_i(\pi_i^*, \pi_{-i}) \geq u_i(\pi_i, \pi_{-i}) \quad \forall \pi_i \in \Pi_i, \forall i \in N, $$

where $\pi_i^*$ is agent iii’s equilibrium strategy, $\pi_{-i}$ are the strategies of other agents, and $\Pi_i$ is the set of possible strategies for agent $i$.

In large-scale MARL, achieving Nash Equilibria is challenging due to the combinatorial explosion of action spaces. Approximation methods, such as fictitious play and gradient-based equilibrium search, are often employed.

While zero-sum games $\sum_{i \in N} u_i(a) = 0$ assume strictly adversarial interactions, general-sum games allow for partial alignment of agent objectives:

$$\sum_{i \in N} u_i(a) \neq 0.$$

This extension enables modeling scenarios where agents may balance competition and cooperation dynamically.

Bayesian games further extend non-cooperative frameworks to settings of incomplete information. Each agent iii is characterized by a type $\theta_i$, drawn from a probability distribution $P(\Theta)$. The expected utility for an agent becomes:

$$ \mathbb{E}_{\theta_{-i} \sim P(\Theta)}[u_i(a_i, a_{-i}, \theta)], $$

where $\theta_{-i}$ are the types of other agents. Bayesian games are particularly relevant in uncertain environments like cybersecurity, where agents infer opponents’ strategies from noisy observations.

In MARL, adversarial training uses non-cooperative game theory to improve agent robustness. An agent trains against an adversary designed to exploit its weaknesses, iteratively refining strategies. Self-play extends this by allowing agents to train against themselves or clones, encouraging exploration of diverse strategies and convergence to equilibrium.

For example, adversarial training in autonomous driving involves designing adversarial agents that mimic real-world traffic anomalies, enabling the primary agent to learn robust strategies.

Non-cooperative game theory is central to complex systems like autonomous traffic control, where each vehicle (agent) optimizes its path while competing for shared road resources. Similarly, in cybersecurity, attackers and defenders engage in a dynamic, adversarial game, requiring real-time strategic adaptation.

Achieving convergence to equilibrium in non-cooperative MARL is non-trivial. Agents may oscillate between strategies, particularly in competitive environments with sparse rewards or conflicting objectives. Addressing these challenges requires robust learning algorithms, such as policy gradient methods augmented with regularization techniques to stabilize learning dynamics.

The following Rust implementation demonstrates zero-sum and non-zero-sum game simulations, adversarial training setups, and Bayesian MARL frameworks in dynamic environments. The Rust program models a non-cooperative game with utility matrices for two players and visualizes their utilities. It supports computing basic Nash equilibria and simulating general-sum games to evaluate the utilities achieved by each player's strategy. Additionally, the program implements visualization of the utility matrices using heatmaps, offering a graphical representation of how each player's strategies influence their payoffs.

use ndarray::{Array2};
use rand::Rng;
use plotters::prelude::*;

/// Represents a non-cooperative game with utility matrices for two players.
struct NonCooperativeGame {
    utility_matrix_p1: Array2<f64>,
    utility_matrix_p2: Array2<f64>,
}

impl NonCooperativeGame {
    fn new(matrix_p1: Array2<f64>, matrix_p2: Array2<f64>) -> Self {
        assert_eq!(matrix_p1.shape(), matrix_p2.shape(), "Utility matrices must have the same shape.");
        Self {
            utility_matrix_p1: matrix_p1,
            utility_matrix_p2: matrix_p2,
        }
    }

    /// Computes a basic Nash Equilibrium using a uniform random strategy.
    fn compute_nash_equilibrium(&self) -> (Vec<f64>, Vec<f64>) {
        let num_strategies = self.utility_matrix_p1.shape()[0];
        let strategy_p1 = vec![1.0 / num_strategies as f64; num_strategies]; // Uniform distribution
        let strategy_p2 = vec![1.0 / num_strategies as f64; num_strategies];
        (strategy_p1, strategy_p2)
    }

    /// Simulates a general-sum game and computes the utilities for both players.
    fn simulate_general_sum_game(&self, strategy_p1: &[f64], strategy_p2: &[f64]) -> (f64, f64) {
        let mut utility_p1 = 0.0;
        let mut utility_p2 = 0.0;

        for i in 0..strategy_p1.len() {
            for j in 0..strategy_p2.len() {
                utility_p1 += strategy_p1[i] * strategy_p2[j] * self.utility_matrix_p1[[i, j]];
                utility_p2 += strategy_p1[i] * strategy_p2[j] * self.utility_matrix_p2[[i, j]];
            }
        }

        (utility_p1, utility_p2)
    }

    /// Visualizes the utility matrices as heatmaps.
 /// Visualizes the utility matrices as heatmaps.
fn visualize_matrices(&self) -> Result<(), Box<dyn std::error::Error>> {
    let root = BitMapBackend::new("utility_matrices.png", (800, 400)).into_drawing_area();
    root.fill(&WHITE)?;

    let (left, right) = root.split_horizontally(400); // Split horizontally into two equal parts

    // Plot Player 1's utility matrix
    let mut chart_p1 = ChartBuilder::on(&left)
        .caption("Player 1 Utility Matrix", ("sans-serif", 20))
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..self.utility_matrix_p1.nrows(), 0..self.utility_matrix_p1.ncols())?;

    chart_p1.configure_mesh().draw()?;

    chart_p1.draw_series(self.utility_matrix_p1.indexed_iter().map(|((i, j), &value)| {
        Rectangle::new(
            [(i, j), (i + 1, j + 1)],
            HSLColor(value / 10.0, 0.5, 0.5).filled(),
        )
    }))?;

    // Plot Player 2's utility matrix
    let mut chart_p2 = ChartBuilder::on(&right)
        .caption("Player 2 Utility Matrix", ("sans-serif", 20))
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..self.utility_matrix_p2.nrows(), 0..self.utility_matrix_p2.ncols())?;

    chart_p2.configure_mesh().draw()?;

    chart_p2.draw_series(self.utility_matrix_p2.indexed_iter().map(|((i, j), &value)| {
        Rectangle::new(
            [(i, j), (i + 1, j + 1)],
            HSLColor(value / 10.0, 0.5, 0.5).filled(),
        )
    }))?;

    Ok(())
}

}

/// Simulates a Bayesian game with uncertain agent types.
fn simulate_bayesian_game() {
    let mut rng = rand::thread_rng();

    let types_p1 = vec![0.6, 0.4]; // Probabilities for Player 1's type
    let types_p2 = vec![0.7, 0.3]; // Probabilities for Player 2's type

    let payoffs = [
        // Payoff matrix based on agent types
        vec![
            Array2::from_shape_vec((2, 2), vec![3.0, 0.0, 5.0, 1.0]).unwrap(),
            Array2::from_shape_vec((2, 2), vec![4.0, 1.0, 2.0, 3.0]).unwrap(),
        ],
        vec![
            Array2::from_shape_vec((2, 2), vec![2.0, 3.0, 1.0, 4.0]).unwrap(),
            Array2::from_shape_vec((2, 2), vec![1.0, 2.0, 3.0, 4.0]).unwrap(),
        ],
    ];

    let chosen_type_p1 = if rng.gen::<f64>() < types_p1[0] { 0 } else { 1 };
    let chosen_type_p2 = if rng.gen::<f64>() < types_p2[0] { 0 } else { 1 };

    let utility_matrix = &payoffs[chosen_type_p1][chosen_type_p2];

    println!(
        "Simulating Bayesian Game: Player 1 Type: {}, Player 2 Type: {}",
        chosen_type_p1, chosen_type_p2
    );
    println!("Utility Matrix:\n{:?}", utility_matrix);
}

fn main() -> Result<(), Box<dyn std::error::Error>> {
    let utility_matrix_p1 = Array2::from_shape_vec((2, 2), vec![3.0, 0.0, 5.0, 1.0]).unwrap();
    let utility_matrix_p2 = Array2::from_shape_vec((2, 2), vec![3.0, 5.0, 0.0, 1.0]).unwrap();
    let game = NonCooperativeGame::new(utility_matrix_p1, utility_matrix_p2);

    let nash_eq = game.compute_nash_equilibrium();
    println!("Nash Equilibrium: Player 1: {:?}, Player 2: {:?}", nash_eq.0, nash_eq.1);

    let utilities = game.simulate_general_sum_game(&nash_eq.0, &nash_eq.1);
    println!("General-Sum Game Utilities: Player 1: {:.2}, Player 2: {:.2}", utilities.0, utilities.1);

    game.visualize_matrices()?;

    simulate_bayesian_game();

    Ok(())
}

The program defines a NonCooperativeGame struct, which holds the utility matrices for two players. The compute_nash_equilibrium function calculates a simple uniform Nash equilibrium, while the simulate_general_sum_game function computes utilities based on given mixed strategies. The visualization function uses the plotters crate to create heatmaps of the utility matrices, which are saved as an image file. The main function initializes the utility matrices, computes the Nash equilibrium, simulates a general-sum game, and generates the visual representation of the matrices.

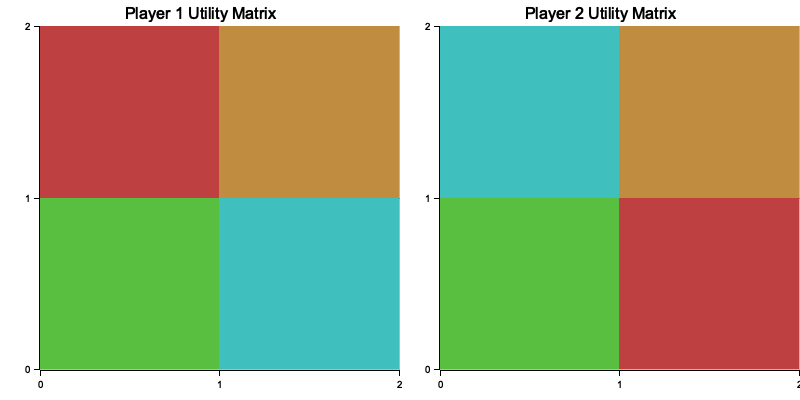
Figure 6: Plotters visualization of player 1 and 2 utility matrix.

The attached image shows the utility matrices for both players. Each cell represents the utility a player receives based on a combination of strategies from both players. For Player 1, higher values (represented by green and teal colors) indicate favorable outcomes, while red represents low payoffs. Similarly, Player 2’s heatmap reflects its optimal and suboptimal outcomes. Comparing the matrices reveals how different strategy combinations yield varying payoffs for each player, highlighting the interdependence of their decisions in the game. This visualization helps analyze strategic advantages and areas where one player might outperform the other.

Non-cooperative game theory is pivotal for analyzing and optimizing competitive interactions in MARL. By extending classical frameworks to general-sum and Bayesian settings, it provides robust tools for modeling adversarial and uncertain environments. Practical implementations in Rust, as demonstrated, offer high-performance simulations that enable MARL researchers and practitioners to tackle real-world challenges, such as autonomous systems and security applications, with precision and scalability.

12.4. Evolutionary Game Theory for MARL link

Evolutionary game theory extends classical game theory by introducing the concepts of adaptation and natural selection into the strategic decision-making framework. Unlike classical game theory, which assumes rational agents acting with fixed strategies, evolutionary game theory focuses on populations of agents that evolve their strategies over time based on performance and interactions. This paradigm is particularly well-suited for modeling and analyzing the dynamics of large-scale Multi-Agent Reinforcement Learning (MARL) systems, where agents must adapt to changing environments and the behaviors of others. The integration of evolutionary dynamics, such as replication, mutation, and selection, enables these systems to exhibit emergent behaviors, achieve robust optimization, and thrive in complex, dynamic settings. Applications of evolutionary game theory in MARL span a diverse range of domains, each leveraging its capacity to model adaptation and population dynamics effectively.

Figure 7: Use cases and applications of evolutionary game theory in MARL.

In autonomous transportation systems, evolutionary game theory helps optimize the behavior of large populations of agents, such as autonomous vehicles, that must interact in complex traffic environments. For example, evolutionary dynamics can model how driving strategies, such as aggressive or cooperative behavior, spread within a population of vehicles. Over time, strategies that lead to fewer accidents or reduced congestion become dominant, enabling the emergence of safer and more efficient traffic patterns. This approach can also inform the design of adaptive traffic management systems, where signal timings and routing algorithms evolve based on real-time data to optimize overall traffic flow.

In financial markets, evolutionary game theory provides a framework for analyzing how trading strategies evolve within a population of agents, such as algorithmic traders. Agents employ strategies ranging from simple heuristic rules to sophisticated machine learning models, and evolutionary dynamics determine which strategies persist based on their performance. For instance, agents that exploit arbitrage opportunities or adapt quickly to market trends gain a competitive edge, while less effective strategies fade over time. Evolutionary MARL models can simulate these dynamics to predict market behavior, test the robustness of trading algorithms, and identify strategies that are resilient to market fluctuations and adversarial agents.

In the realm of cybersecurity, evolutionary game theory is applied to model the ongoing arms race between attackers and defenders in networked systems. Attack strategies, such as phishing or denial-of-service attacks, evolve over time as attackers adapt to countermeasures. Similarly, defensive strategies, including intrusion detection systems and adaptive firewalls, must continuously evolve to address emerging threats. Evolutionary MARL frameworks enable the simulation of these dynamics, allowing defenders to test and refine their strategies in a controlled environment. This approach is particularly valuable for designing systems that remain robust against sophisticated, adaptive adversaries.

In healthcare and epidemiology, evolutionary game theory aids in modeling the spread of behaviors, such as vaccination or compliance with public health guidelines, within populations. Agents representing individuals in a population adapt their behaviors based on perceived risks, benefits, and social influences. Evolutionary dynamics help predict how these behaviors evolve over time and their impact on public health outcomes. For example, vaccination strategies that maximize herd immunity may become dominant, while non-compliant behaviors diminish. MARL models incorporating evolutionary principles can also optimize resource allocation in public health campaigns, such as distributing vaccines or deploying healthcare workers to areas of greatest need.

Smart grids represent another compelling application of evolutionary game theory in MARL. In energy markets, households and businesses act as agents that adapt their energy consumption and production strategies based on pricing signals and grid conditions. Evolutionary dynamics allow these systems to identify and propagate strategies that maximize efficiency, such as shifting energy usage to off-peak hours or integrating renewable energy sources. Over time, the grid evolves toward a more stable and efficient equilibrium, reducing costs and environmental impact. This adaptive approach is particularly valuable for managing large, decentralized energy systems with diverse participants.

In robotics and swarm systems, evolutionary game theory models the adaptation and coordination of large groups of robots or drones performing tasks like search-and-rescue, exploration, or delivery. Strategies for task allocation, navigation, and communication evolve as agents interact with each other and the environment. For instance, in a search-and-rescue mission, drones may initially explore randomly but gradually converge on collaborative strategies that maximize coverage and efficiency. Evolutionary MARL enables the simulation of these dynamics, facilitating the design of swarm systems that are adaptive, resilient, and capable of operating in unpredictable environments.

In ecosystem management and conservation, evolutionary game theory helps model interactions among species or stakeholders in natural resource management. Agents representing species, industries, or conservation organizations adapt their strategies based on resource availability, environmental conditions, and competition. For example, strategies for harvesting renewable resources, such as fisheries or forests, evolve to balance economic goals with sustainability. Evolutionary MARL can simulate these dynamics to inform policies that promote long-term ecological balance and equitable resource distribution.

Decentralized finance (DeFi) and blockchain ecosystems are also fertile ground for evolutionary game theory. Agents representing participants in DeFi systems, such as liquidity providers or borrowers, adapt their strategies based on market conditions and incentives. Evolutionary dynamics enable the modeling of how these strategies evolve, identifying optimal behaviors that enhance system efficiency and security. For instance, evolutionary MARL can help design incentive structures that discourage malicious behaviors, such as double-spending or front-running, while promoting healthy participation.

In the context of education and learning systems, evolutionary game theory models how teaching methods or learning strategies propagate within a population of learners. For example, in online education platforms, strategies for engagement, collaboration, and knowledge sharing evolve based on their effectiveness. Evolutionary MARL allows platforms to optimize these strategies dynamically, enhancing learning outcomes for diverse populations of students.

The practical implementation of evolutionary game theory in MARL benefits greatly from Rust’s performance, safety, and concurrency capabilities. By leveraging Rust, developers can create scalable simulations that model the adaptive dynamics of large agent populations in real time. These simulations enable the exploration of emergent behaviors, the optimization of strategies, and the design of robust, adaptive systems for real-world applications. Whether in autonomous transportation, financial markets, cybersecurity, or smart grids, evolutionary game theory provides the tools to harness the power of adaptation and emergence, addressing some of the most complex challenges in modern multi-agent systems.

At the heart of evolutionary game theory lies replicator dynamics, which describe how the proportion of agents using a particular strategy changes over time. Given a population of agents with strategies $x_1, x_2, \dots, x_n$, the replicator equation is expressed as:

$$ \dot{x}_i = x_i \left( f_i(x) - \bar{f}(x) \right), $$

where:

• $x_i$ is the proportion of the population using strategy $i$.

• $f_i(x)$ is the fitness of strategy $i$, determined by the utility function.

• $\bar{f}(x) = \sum_{j} x_j f_j(x)$ is the average fitness of the population.

Strategies with higher-than-average fitness grow in proportion, while others diminish, leading to emergent equilibrium behavior.

In large-scale MARL, agent interactions can be modeled using evolutionary graphs, where nodes represent agents and edges denote potential interactions. The state of the system evolves through localized strategy updates based on the replicator equation applied within neighborhoods of the graph. This approach captures spatial and network effects in agent populations, enabling realistic modeling of distributed systems.

Evolutionary equilibria extend the concept of Nash Equilibria by incorporating stability criteria under evolutionary pressures. A strategy $x^*$ is considered evolutionarily stable if, when a small proportion of the population adopts a mutant strategy $y$, the incumbents retain a higher average fitness:

$$ f(x^*, x^*) > f(y, x^*), $$

or, if $f(x^, x^) = f(y, x^)$, then $f(x^, y) > f(y, y)$.

In MARL, stability of evolutionary equilibria ensures robustness of learned policies against perturbations or adversarial strategies.

Evolutionary game theory draws inspiration from biological processes like natural selection and genetic mutation to design adaptive learning mechanisms. In MARL, these bio-inspired approaches enable agents to evolve strategies that are robust to dynamic and uncertain environments.

Combining evolutionary strategies with deep reinforcement learning enhances exploration and policy diversity. Evolutionary algorithms, such as Genetic Algorithms (GA) and Covariance Matrix Adaptation Evolution Strategy (CMA-ES), are often employed to optimize neural network policies by evolving weights and hyperparameters.

Evolutionary game theory is particularly effective in solving complex optimization problems, such as traffic flow optimization, resource allocation, and distributed control. By simulating adaptive agent populations, these methods uncover efficient solutions through emergent behaviors.

This Rust implementation models an evolutionary game using replicator dynamics, a framework commonly used in game theory to study the evolution of strategies in populations over time. The code simulates strategy adaptation within a population using a payoff matrix to define the interactions between three distinct strategies. The system evolves the population's strategy distribution over multiple iterations, identifying stable equilibria or convergence points. Additionally, the program generates visualizations of the evolutionary dynamics to provide insights into the behavior of different strategies.

use ndarray::{Array1, Array2};
use plotters::prelude::*;
use std::error::Error;

/// Represents an evolutionary game with replicator dynamics.
struct EvolutionaryGame {
    payoffs: Array2<f64>,
}

impl EvolutionaryGame {
    fn new(payoffs: Array2<f64>) -> Self {
        assert_eq!(
            payoffs.nrows(),
            payoffs.ncols(),
            "Payoff matrix must be square"
        );
        Self { payoffs }
    }

    /// Computes the fitness of each strategy based on the current population distribution.
    fn compute_fitness(&self, population: &Array1<f64>) -> Array1<f64> {
        self.payoffs.dot(population)
    }

    /// Evolves the population using replicator dynamics.
    fn evolve_population(&self, population: &Array1<f64>, time_step: f64) -> Array1<f64> {
        let fitness = self.compute_fitness(population);
        let average_fitness = population.dot(&fitness);
        population
            + (population * (&fitness - Array1::from_elem(population.len(), average_fitness)))
                .mapv(|x| x * time_step)
    }
}

/// Simulates evolutionary dynamics for a given number of iterations.
fn simulate_evolution(
    game: &EvolutionaryGame,
    initial_population: Array1<f64>,
    iterations: usize,
    time_step: f64,
) -> Vec<Array1<f64>> {
    let mut populations = vec![initial_population.clone()];
    let mut current_population = initial_population;

    for i in 0..iterations {
        let next_population = game.evolve_population(&current_population, time_step);

        // Log current state
        println!(
            "Iteration {}: Population = {:?}, Fitness = {:?}",
            i + 1,
            current_population,
            game.compute_fitness(&current_population)
        );

        // Check for stability
        if (next_population.clone() - &current_population)
            .iter()
            .all(|&x| x.abs() < 1e-6)
        {
            println!("Population has converged at iteration {}", i + 1);
            break;
        }

        populations.push(next_population.clone());
        current_population = next_population;
    }

    populations
}

/// Visualizes the evolution of strategy proportions over time.
fn visualize_evolution(
    populations: &[Array1<f64>],
    filename: &str,
) -> Result<(), Box<dyn Error>> {
    let root = BitMapBackend::new(filename, (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let num_strategies = populations[0].len();
    let max_time = populations.len();

    let mut chart = ChartBuilder::on(&root)
        .caption("Evolutionary Dynamics", ("sans-serif", 20))
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..max_time, 0.0..1.0)?;

    chart
        .configure_mesh()
        .x_desc("Iterations")
        .y_desc("Population Proportion")
        .draw()?;

    for strategy in 0..num_strategies {
        let series = populations
            .iter()
            .enumerate()
            .map(|(t, population)| (t, population[strategy]));
        chart
            .draw_series(LineSeries::new(series, &Palette99::pick(strategy)))?
            .label(format!("Strategy {}", strategy + 1));
    }

    chart.configure_series_labels().border_style(&BLACK).draw()?;

    Ok(())
}

fn main() -> Result<(), Box<dyn Error>> {
    // Define the payoff matrix for a three-strategy game.
    let payoffs = Array2::from_shape_vec(
        (3, 3),
        vec![
            0.0, 2.0, 1.0, // Payoff for strategy 1
            1.0, 0.0, 2.0, // Payoff for strategy 2
            2.0, 1.0, 0.0, // Payoff for strategy 3
        ],
    )
    .unwrap();

    let game = EvolutionaryGame::new(payoffs);

    // Validate initial population distribution.
    let initial_population = Array1::from_vec(vec![0.4, 0.3, 0.3]);
    assert!(
        (initial_population.sum() - 1.0_f64).abs() < 1e-6,
        "Initial population must sum to 1.0"
    );

    // Simulate the evolution of populations.
    let iterations = 100;
    let time_step = 0.1;
    let populations = simulate_evolution(&game, initial_population, iterations, time_step);

    // Visualize the evolution.
    visualize_evolution(&populations, "evolutionary_dynamics_advanced.png")?;

    Ok(())
}

The program begins by defining a payoff matrix for a three-strategy evolutionary game. Using the replicator dynamics model, the program computes the fitness of each strategy based on the current population distribution and iteratively updates the population using these fitness values. The dynamics simulate the process where successful strategies grow in proportion to their fitness relative to the average fitness of the population. The simulation tracks the changes in strategy proportions over time and stops if the population converges. The resulting proportions of strategies are visualized in a line chart, illustrating the evolution of strategy proportions across iterations, allowing users to analyze trends such as dominance, coexistence, or equilibrium states among strategies.

Evolutionary game theory offers a powerful paradigm for modeling adaptive behaviors in MARL. Through replicator dynamics and graph-based evolutionary frameworks, it enables robust learning and optimization in large-scale agent systems. By integrating these concepts with Rust’s computational and visualization capabilities, this chapter equips practitioners to design, simulate, and analyze evolutionary dynamics for solving real-world multi-agent problems.

12.5. Mixed-Strategy and Correlated Equilibria in MARL link

Mixed-strategy and correlated equilibria build on foundational game-theoretic concepts, providing sophisticated frameworks for modeling and solving complex strategic interactions. Unlike pure strategies, which dictate deterministic choices, mixed strategies allow agents to adopt probabilistic approaches, enabling flexibility and adaptability in dynamic environments. Correlated equilibria extend this further by introducing coordination through shared signals, enabling agents to align their actions in ways that maximize collective efficiency or minimize conflict. These concepts are invaluable in Multi-Agent Reinforcement Learning (MARL), where agents operate in environments characterized by uncertainty, incomplete information, and constraints on communication. The integration of these equilibria into MARL unlocks practical solutions for high-dimensional, real-world problems across diverse industries.

Figure 8: Enhanced coordination and efficiency for MAS.

In autonomous transportation, mixed-strategy and correlated equilibria play a crucial role in enabling efficient and safe coordination among autonomous vehicles. For example, at a busy intersection, vehicles must decide probabilistically whether to yield, proceed, or take alternate routes, balancing their objectives with those of other vehicles. A correlated equilibrium might involve a traffic signal acting as a shared signal, coordinating vehicle actions to prevent collisions and minimize delays. Mixed strategies are also valuable in ride-sharing systems, where vehicles probabilistically decide on routes or pickups to maximize efficiency while avoiding overcrowding in certain areas. By integrating these equilibria into MARL frameworks, autonomous transportation systems can achieve robust coordination in high-traffic scenarios with limited direct communication among vehicles.

In financial markets, mixed-strategy equilibria enable trading agents to diversify their strategies, reducing the predictability of their actions and mitigating risks in competitive environments. For instance, an agent might adopt a probabilistic mix of strategies for buying, selling, or holding assets, ensuring resilience against market volatility and adversarial strategies from other traders. Correlated equilibria enhance coordination in scenarios like auctions or resource allocation, where participants can leverage shared signals, such as market indicators, to align their actions for mutually beneficial outcomes. These equilibria are particularly useful in decentralized finance (DeFi) systems, where agents operate autonomously but must adhere to shared protocols for fair and efficient resource distribution.

In cybersecurity, mixed-strategy equilibria enable defenders to adopt unpredictable defense mechanisms, making it harder for attackers to exploit vulnerabilities. For example, a defender might probabilistically allocate resources to monitor different parts of a network, ensuring comprehensive coverage while minimizing redundancy. Correlated equilibria facilitate coordination among multiple defenders, such as firewalls, intrusion detection systems, and endpoint security tools, allowing them to respond effectively to emerging threats. This is particularly valuable in distributed systems, where coordinated actions are essential to counter sophisticated, multi-vector cyberattacks.

In telecommunications and network management, mixed-strategy equilibria optimize resource allocation in scenarios involving competing users or devices. For example, in a wireless network, devices might probabilistically choose transmission frequencies or power levels to minimize interference and maximize throughput. Correlated equilibria further enhance efficiency by allowing devices to coordinate their choices based on shared signals, such as network congestion levels or quality-of-service indicators. This approach ensures fair and efficient utilization of network resources, particularly in high-demand scenarios like 5G and IoT networks.

In logistics and supply chain management, mixed-strategy equilibria enable agents representing suppliers, distributors, and retailers to adapt to dynamic demand and supply conditions. For instance, a retailer might probabilistically decide on inventory replenishment levels based on fluctuating consumer demand, while a supplier coordinates production schedules with downstream partners through correlated signals like shared demand forecasts. These equilibria facilitate efficient resource allocation, reduce waste, and enhance supply chain resilience, particularly in scenarios with high uncertainty, such as during global disruptions or seasonal variations.

In smart grids and energy markets, mixed-strategy equilibria enable households and businesses to probabilistically adjust their energy consumption based on pricing signals and grid conditions. For example, during peak demand periods, users might probabilistically reduce or shift their energy usage to avoid high costs while ensuring essential needs are met. Correlated equilibria further enhance coordination in decentralized energy systems, where agents use shared signals, such as renewable energy availability, to align their consumption and production decisions. This approach supports grid stability, promotes renewable energy integration, and reduces overall energy costs.

In healthcare, mixed-strategy and correlated equilibria facilitate decision-making in resource allocation and patient care coordination. For instance, hospitals might probabilistically allocate resources like ICU beds or ventilators based on predicted demand, ensuring equitable access and efficient utilization. Correlated equilibria enhance collaboration among hospitals, clinics, and public health agencies by coordinating actions such as vaccine distribution or emergency response efforts through shared signals like epidemiological data. These equilibria ensure that healthcare systems remain adaptive and responsive to dynamic and uncertain conditions.

In gaming and entertainment, mixed-strategy equilibria enable non-player characters (NPCs) and game AI to adopt unpredictable behaviors, enhancing the challenge and engagement for players. For example, an NPC in a strategy game might probabilistically choose between offensive and defensive actions, making it harder for players to predict and counter its moves. Correlated equilibria further enhance multiplayer experiences by facilitating coordinated actions among NPCs or players, such as forming alliances or executing complex strategies based on shared objectives or signals.

In environmental management, mixed-strategy equilibria enable stakeholders to balance economic and ecological objectives in resource management. For instance, fisheries might probabilistically limit catches based on stock levels, ensuring sustainable practices while maintaining livelihoods. Correlated equilibria further support collaboration among industries, governments, and conservation organizations by aligning actions such as pollution control, habitat restoration, or resource sharing through shared environmental indicators.

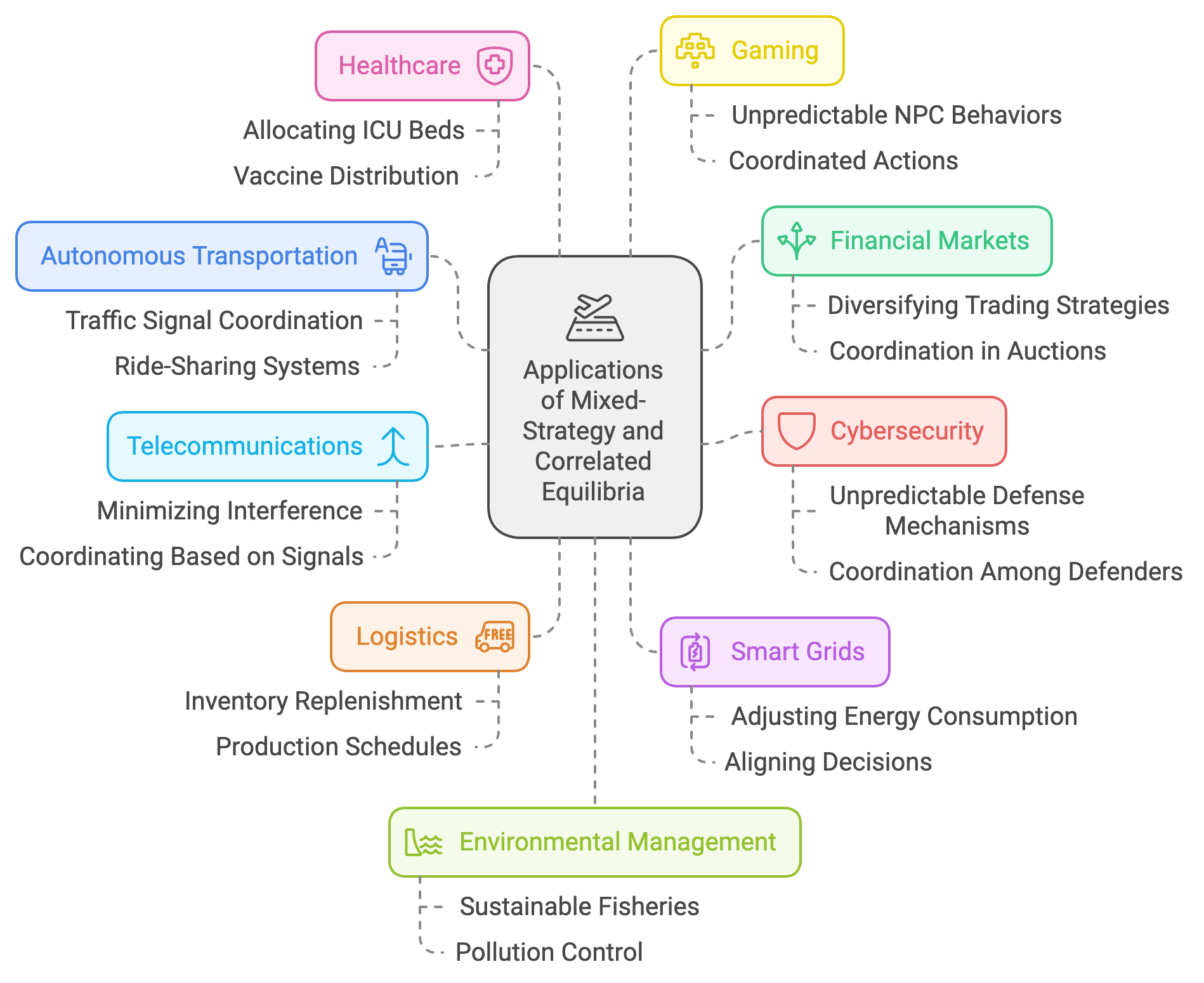
Figure 9: Applications and use cases for mixed strategy and correlated equilibria in MAS.

The practical implementation of mixed-strategy and correlated equilibria in MARL benefits significantly from Rust's performance and safety features. Rust's concurrency model and memory safety ensure efficient handling of large-scale simulations involving high-dimensional action spaces and dynamic agent interactions. For example, Rust can be used to simulate transportation networks, financial markets, or energy systems, enabling the exploration of equilibrium strategies in realistic, high-stakes environments. By integrating these advanced equilibrium concepts into MARL, researchers and practitioners can design adaptive, scalable, and resilient systems that address the complexities of modern multi-agent interactions.

A mixed strategy for an agent is a probability distribution over its action space. In contrast to pure strategies, which select a single action deterministically, mixed strategies allow agents to randomize their choices. For an $n$-agent game, let $\pi_i(a_i)$ represent the probability of agent $i$ selecting action $a_i$. The joint mixed strategy profile is defined as $\Pi = (\pi_1, \pi_2, \dots, \pi_n)$.

The expected utility for agent $i$ under a mixed-strategy profile is given by:

$$ u_i(\Pi) = \sum_{a \in A} \pi(a) \cdot u_i(a), $$

where $A = A_1 \times A_2 \times \cdots \times A_n$ is the joint action space, $\pi(a)$ is the joint probability of action $a$, and $u_i(a)$ is the utility of $i$ for aaa.

A mixed-strategy Nash equilibrium satisfies:

$$ u_i(\pi_i^*, \pi_{-i}) \geq u_i(\pi_i, \pi_{-i}) \quad \forall \pi_i \in \Delta(A_i), \forall i \in N, $$

where $\Delta(A_i)$ is the probability simplex over $A_i$, and $\pi_{-i}$ are the strategies of all agents except $i$.

High-dimensional action spaces pose computational challenges due to the exponential growth of $A$. Techniques like sparse approximations and Monte Carlo sampling are used to make mixed-strategy computation tractable.

The correlated equilibrium generalizes the Nash equilibrium by allowing agents to condition their strategies on shared signals. A signaling mechanism provides recommendations $\sigma$ to agents, and the agents optimize their responses under the assumption that others will follow the signal.

Mathematically, a correlated equilibrium is defined by:

$$ \mathbb{E}[u_i(a_i, a_{-i}) \mid \sigma] \geq \mathbb{E}[u_i(a_i', a_{-i}) \mid \sigma] \quad \forall a_i, a_i' \in A_i, \forall i \in N. $$

This formulation reduces the complexity of coordination in MARL, particularly in environments with communication constraints, as agents rely on signals instead of direct interaction.

In MARL settings with incomplete information, agents use probabilistic reasoning to handle uncertainties about other agents’ strategies and the environment’s state. Bayesian game frameworks are often combined with mixed and correlated equilibria to model these interactions. Agents maximize their expected utilities over posterior beliefs:

$$ \pi_i^*(\theta_i) = \arg\max_{\pi_i} \mathbb{E}[u_i(a_i, a_{-i}, \theta) \mid \theta_i], $$

where $\theta_i$ represents agent iii’s private type.

Achieving robust coordination in partially observable environments requires integrating mixed and correlated equilibria into MARL algorithms. By leveraging signaling mechanisms, agents can achieve equilibrium states without explicit communication, significantly reducing overhead. For example, in logistics applications, correlated equilibria enable fleet vehicles to coordinate routes using shared dispatch signals.

Mixed strategies and correlated equilibria have transformative applications across real-world domains by enabling probabilistic decision-making and efficient coordination in complex systems. In finance, mixed strategies capture the probabilistic behaviors of market participants, aiding in portfolio optimization, risk management, and adaptive trading strategies to navigate volatile markets. In logistics, these frameworks empower agents to coordinate resource allocation and scheduling under uncertain demand, optimizing supply chain efficiency and minimizing delays. For resource optimization, mixed and correlated equilibria drive equitable and efficient sharing of resources in decentralized energy grids, ensuring balanced energy consumption and production, and in computational infrastructure, where they dynamically allocate processing power and bandwidth to meet fluctuating demands. These applications highlight the adaptability and scalability of mixed-strategy and correlated equilibrium concepts in addressing uncertainty and complexity in diverse industries.

The provided Rust implementation showcases an advanced game-theoretic model that supports high-dimensional mixed-strategy equilibria, correlated equilibria through shared signals, and performance evaluation under uncertainty. It employs utility matrices to represent payoff structures for two agents and leverages dynamically generated signals to simulate coordination and interdependence between agents. This code integrates essential game-theoretic concepts, such as mixed strategies and correlated equilibria, with features like signal-based decision-making and robust validation for strategy correctness, offering a comprehensive framework for analyzing multi-agent interactions.

use ndarray::{Array1, Array2};
use rand::Rng;

/// Represents a game with utility matrices for two agents.
struct Game {
    utility_matrix_p1: Array2<f64>,
    utility_matrix_p2: Array2<f64>,
}

impl Game {
    fn new(matrix_p1: Array2<f64>, matrix_p2: Array2<f64>) -> Self {
        assert_eq!(
            matrix_p1.shape(),
            matrix_p2.shape(),
            "Utility matrices for both players must have the same dimensions."
        );
        Self {
            utility_matrix_p1: matrix_p1,
            utility_matrix_p2: matrix_p2,
        }
    }

    /// Validates a mixed strategy to ensure it sums to 1 and has non-negative values.
    fn validate_strategy(strategy: &Array1<f64>) {
        assert!(
            (strategy.sum() - 1.0).abs() < 1e-6,
            "Mixed strategy probabilities must sum to 1."
        );
        assert!(
            strategy.iter().all(|&x| x >= 0.0),
            "Mixed strategy probabilities must be non-negative."
        );
    }

    /// Computes the expected utility for a mixed strategy.
    fn expected_utility(
        &self,
        strategy_p1: &Array1<f64>,
        strategy_p2: &Array1<f64>,
        player: usize,
    ) -> f64 {
        Self::validate_strategy(strategy_p1);
        Self::validate_strategy(strategy_p2);

        let utility_matrix = if player == 1 {
            &self.utility_matrix_p1
        } else {
            &self.utility_matrix_p2
        };

        strategy_p1.dot(&utility_matrix.dot(strategy_p2))
    }

    /// Generates signals dynamically for correlated equilibria.
    fn generate_signals(&self, num_signals: usize) -> Vec<(usize, usize, f64)> {
        let mut rng = rand::thread_rng();
        let num_actions_p1 = self.utility_matrix_p1.nrows();
        let num_actions_p2 = self.utility_matrix_p2.ncols();

        let mut signals = vec![];
        let mut total_probability = 0.0;

        for _ in 0..num_signals {
            let action_p1 = rng.gen_range(0..num_actions_p1);
            let action_p2 = rng.gen_range(0..num_actions_p2);
            let prob = rng.gen_range(0.1..0.5); // Random probability for each signal
            total_probability += prob;
            signals.push((action_p1, action_p2, prob));
        }

        // Normalize probabilities to ensure they sum to 1.
        for signal in &mut signals {
            signal.2 /= total_probability;
        }

        signals
    }

    /// Simulates a correlated equilibrium based on shared signals.
    fn correlated_equilibrium(&self, signals: Vec<(usize, usize, f64)>) -> Vec<f64> {
        let mut strategy_p1 = Array1::zeros(self.utility_matrix_p1.nrows());
        let mut strategy_p2 = Array1::zeros(self.utility_matrix_p2.ncols());

        for (a1, a2, prob) in signals {
            strategy_p1[a1] += prob;
            strategy_p2[a2] += prob;
        }

        strategy_p1 /= strategy_p1.sum();
        strategy_p2 /= strategy_p2.sum();

        vec![
            self.expected_utility(&strategy_p1, &strategy_p2, 1),
            self.expected_utility(&strategy_p1, &strategy_p2, 2),
        ]
    }
}

fn main() {
    // Define utility matrices for two players.
    let utility_matrix_p1 = Array2::from_shape_vec((3, 3), vec![
        3.0, 0.0, 1.0, 
        1.0, 2.0, 0.0, 
        0.0, 1.0, 2.0
    ]).unwrap();

    let utility_matrix_p2 = Array2::from_shape_vec((3, 3), vec![
        3.0, 1.0, 0.0, 
        0.0, 2.0, 1.0, 
        1.0, 0.0, 2.0
    ]).unwrap();

    let game = Game::new(utility_matrix_p1, utility_matrix_p2);

    // Define mixed strategies for both players.
    let strategy_p1 = Array1::from_vec(vec![0.4, 0.3, 0.3]);
    let strategy_p2 = Array1::from_vec(vec![0.5, 0.2, 0.3]);

    // Compute expected utilities for mixed strategies.
    let utility_p1 = game.expected_utility(&strategy_p1, &strategy_p2, 1);
    let utility_p2 = game.expected_utility(&strategy_p1, &strategy_p2, 2);

    println!("Expected Utility for Player 1: {:.2}", utility_p1);
    println!("Expected Utility for Player 2: {:.2}", utility_p2);

    // Generate and simulate a correlated equilibrium.
    let signals = game.generate_signals(5); // Dynamically generate signals
    println!("Generated Signals: {:?}", signals);

    let equilibrium = game.correlated_equilibrium(signals);

    println!(
        "Correlated Equilibrium Utilities: Player 1: {:.2}, Player 2: {:.2}",
        equilibrium[0], equilibrium[1]
    );
}

The code defines a Game struct with utility matrices for two agents, representing their respective payoffs. It computes the expected utility for agents using mixed strategies by performing matrix operations on the strategy vectors and utility matrices. The correlated_equilibrium function simulates equilibria based on shared signals, dynamically generated using the generate_signals function, which normalizes probabilities to ensure they form a valid distribution. These signals guide the agents toward correlated strategies, reflecting coordination and dependencies. The code also validates strategies to ensure proper probability distributions and compatibility of utility matrices. Finally, it demonstrates these concepts through an example, computing the expected utilities for predefined mixed strategies and dynamically generated correlated equilibria, providing insights into cooperative and competitive behaviors in multi-agent systems.

Mixed-strategy and correlated equilibria provide versatile tools for achieving robust coordination and adaptation in MARL. By extending classical equilibrium concepts to probabilistic and signal-based frameworks, these methods enable agents to operate effectively in high-dimensional, uncertain, and communication-constrained environments. The Rust implementation demonstrates how to leverage these principles for efficient multi-agent optimization, opening pathways for advanced applications in finance, logistics, and beyond.

12.6. Applications of Game Theory in Real-World MARL link

Game theory in Multi-Agent Reinforcement Learning (MARL) has profound applications in real-world scenarios, where multiple autonomous agents must interact in complex, dynamic environments. By leveraging game-theoretic principles, MARL frameworks can address challenges in fairness, resource optimization, and ethical decision-making while ensuring scalability and adaptability. This section explores mathematical modeling, conceptual integration, and practical implementations of MARL in critical real-world domains such as autonomous vehicles, drone swarms, energy markets, and decentralized finance, with a focus on distributed systems and Rust-based implementations.

In real-world MARL, agents often operate in environments governed by multi-objective optimization problems, where objectives like efficiency, fairness, and sustainability compete. A general mathematical model for MARL in such settings can be expressed as:

$$ \max_{\pi_1, \pi_2, \ldots, \pi_n} \sum_{i=1}^n \mathbb{E}\left[ \sum_{t=0}^\infty \gamma^t u_i(s_t, a_t) \right], $$

subject to:

Fairness constraints: $\text{Fairness constraints: } \mathcal{F}(\pi) \leq \epsilon, \quad \text{Resource constraints: } \mathcal{R}(s, a) \geq \delta.$

Here:

• $\pi_i$ represents the policy of agent $i$,

• $u_i(s_t, a_t)$ is the reward function for agent iii at time ttt,

• $\mathcal{F}(\pi)$ measures deviations from fairness,

• $\mathcal{R}(s, a)$ represents available resources.

Dynamic and heterogeneous environments, such as those involving multiple vehicle types in traffic systems or diverse trading entities in energy markets, require advanced reward functions that adapt to shifting objectives:

$$ u_i(s_t, a_t) = \alpha_i f_\text{efficiency}(s_t, a_t) + \beta_i f_\text{cooperation}(s_t, a_t) + \gamma_i f_\text{sustainability}(s_t, a_t), $$

where $\alpha_i, \beta_i, \gamma_i$ are weights representing the agent's priorities.

In autonomous traffic systems, vehicles (agents) navigate shared road networks while optimizing travel time, fuel efficiency, and safety. Game-theoretic MARL allows agents to balance competitive and cooperative interactions. For example, vehicles can adopt cooperative policies at intersections to minimize congestion, modeled as a correlated equilibrium where agents follow traffic signals.

In drone swarm applications, agents coordinate tasks such as surveillance, delivery, or disaster response. Cooperative strategies optimize shared objectives like coverage or energy efficiency, while competitive strategies address resource contention. Game-theoretic models integrate coalition formation to dynamically allocate tasks among drones.

Energy markets involve autonomous agents (e.g., power producers, consumers, and grid operators) negotiating supply and demand under fluctuating conditions. Game-theoretic MARL supports dynamic pricing and resource allocation, ensuring stability and efficiency in distributed systems. Similarly, decentralized finance (DeFi) platforms use MARL to optimize liquidity provision and minimize risk.

Ethical challenges in applying MARL include ensuring fairness, avoiding bias, and managing unintended consequences. For example, in traffic systems, prioritizing efficiency for one group of vehicles should not unfairly disadvantage others. Incorporating fairness constraints and ethical reward shaping can help align agent behaviors with societal goals.

This Rust implementation models a traffic management system at an intersection using a Multi-Agent Reinforcement Learning (MARL) framework. Each agent (e.g., vehicles or traffic lights) is represented with a strategy that evolves based on a reward matrix describing the interactions between agents. The simulation uses softmax-based updates to ensure the strategies remain valid probability distributions and includes visualization to monitor the evolution of strategies over time.

use ndarray::{Array2, Array1};
use plotters::prelude::*;

/// Represents a traffic intersection with multiple agents.
struct TrafficIntersection {
    reward_matrix: Array2<f64>,
}

impl TrafficIntersection {
    fn new(reward_matrix: Array2<f64>) -> Self {
        Self { reward_matrix }
    }

    /// Simulates traffic flow and returns updated rewards for each agent.
    fn simulate(&self, strategies: &Array1<f64>) -> Array1<f64> {
        self.reward_matrix.dot(strategies)
    }
}

/// Visualizes the evolution of strategies over time.
fn visualize_strategy_evolution(
    strategy_history: &[Array1<f64>],
    filename: &str,
) -> Result<(), Box<dyn std::error::Error>> {
    let root = BitMapBackend::new(filename, (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let num_agents = strategy_history[0].len();
    let max_time = strategy_history.len();

    let mut chart = ChartBuilder::on(&root)
        .caption("Traffic Management Strategy Evolution", ("sans-serif", 20))
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..max_time, 0.0..1.0)?;

    chart.configure_mesh().draw()?;

    for agent in 0..num_agents {
        let series = strategy_history
            .iter()
            .enumerate()
            .map(|(t, strategies)| (t, strategies[agent]));
        chart
            .draw_series(LineSeries::new(series, &Palette99::pick(agent)))
            .unwrap()
            .label(format!("Agent {}", agent + 1));
    }

    chart.configure_series_labels().draw()?;

    Ok(())
}

/// Simulates distributed MARL for traffic management.
fn simulate_traffic_management() -> Result<(), Box<dyn std::error::Error>> {
    let reward_matrix = Array2::from_shape_vec(
        (3, 3),
        vec![
            1.0, -0.5, 0.2,  // Rewards for Agent 1
            -0.3, 1.0, -0.2, // Rewards for Agent 2
            0.1, -0.4, 1.0,  // Rewards for Agent 3
        ],
    )
    .unwrap();

    let intersection = TrafficIntersection::new(reward_matrix);

    let mut strategies = Array1::from(vec![0.4, 0.3, 0.3]); // Initial strategies
    let mut strategy_history = vec![strategies.clone()];

    for _ in 0..50 {
        let rewards = intersection.simulate(&strategies);

        // Update strategies using softmax (to ensure they remain probabilistic)
        let max_reward = rewards.iter().cloned().fold(f64::NEG_INFINITY, f64::max);
        let exp_rewards: Array1<f64> = rewards.mapv(|r| (r - max_reward).exp());
        strategies = &exp_rewards / exp_rewards.sum();

        strategy_history.push(strategies.clone());
    }

    // Visualize the evolution of strategies.
    visualize_strategy_evolution(&strategy_history, "strategy_evolution.png")?;

    println!("Final Strategies: {:?}", strategies);
    Ok(())
}

fn main() -> Result<(), Box<dyn std::error::Error>> {
    simulate_traffic_management()?;
    Ok(())
}

The TrafficIntersection struct encapsulates the reward matrix that governs the interactions between agents. The simulate method calculates rewards for agents based on their current strategies using a dot product with the reward matrix. During the simulation, each agent's strategy is iteratively updated using a softmax function applied to the rewards, ensuring that strategies remain probabilistic. This dynamic process is repeated over several iterations, with the history of strategies recorded. Finally, the visualize_strategy_evolution function uses the plotters crate to generate a chart showing how each agent's strategy evolves over time. The simulation aims to balance agent behavior for optimal traffic flow.

Next, this Rust implementation models a drone swarm performing cooperative and competitive task allocations using dynamic strategies. The simulation incorporates stochastic noise to reflect real-world uncertainties and uses softmax adjustments to ensure task allocation strategies remain valid probability distributions. Additionally, it visualizes the evolution of task allocation strategies over time, providing insights into the swarm's cooperative behavior.

use ndarray::Array1;
use plotters::prelude::*;
use rand::Rng; // Import the Rng trait explicitly.

/// Represents a drone swarm with cooperative and competitive strategies.
struct DroneSwarm {
    num_drones: usize,
    task_rewards: Array1<f64>,
}

impl DroneSwarm {
    fn new(num_drones: usize, task_rewards: Vec<f64>) -> Self {
        assert_eq!(num_drones, task_rewards.len(), "Number of drones must match task rewards");
        Self {
            num_drones,
            task_rewards: Array1::from(task_rewards),
        }
    }

    /// Allocates tasks among drones and calculates total reward.
    fn allocate_tasks(&self, strategies: &Array1<f64>) -> f64 {
        assert_eq!(
            self.num_drones,
            strategies.len(),
            "Strategy length must match the number of drones"
        );
        strategies.dot(&self.task_rewards)
    }

    /// Updates strategies dynamically using a softmax adjustment.
    fn update_strategies(&self, strategies: &Array1<f64>, total_reward: f64, rng: &mut rand::rngs::ThreadRng) -> Array1<f64> {
        // Add stochastic noise to strategies
        let noisy_strategies: Array1<f64> = strategies.mapv(|s| s * (1.0 + rng.gen_range(-0.1..0.1)));

        // Adjust strategies using total reward and normalize with softmax
        let adjusted = noisy_strategies.mapv(|s| (s * total_reward).exp());
        &adjusted / adjusted.sum()
    }
}

/// Simulates the evolution of task allocation among drones.
fn simulate_drone_swarm_evolution() -> Result<(), Box<dyn std::error::Error>> {
    let swarm = DroneSwarm::new(3, vec![10.0, 15.0, 20.0]);

    let mut strategies = Array1::from(vec![0.33, 0.33, 0.34]); // Initial task allocation
    let mut strategy_history = vec![strategies.clone()];
    let mut rng = rand::thread_rng();

    for _ in 0..50 {
        let total_reward = swarm.allocate_tasks(&strategies);
        strategies = swarm.update_strategies(&strategies, total_reward, &mut rng);
        strategy_history.push(strategies.clone());
    }

    // Visualize the evolution of task allocation strategies.
    visualize_strategy_evolution(&strategy_history, "drone_swarm_evolution.png")?;

    println!("Final Strategies: {:?}", strategies);
    Ok(())
}

/// Visualizes the evolution of task allocation among drones over time.
fn visualize_strategy_evolution(
    strategy_history: &[Array1<f64>],
    filename: &str,
) -> Result<(), Box<dyn std::error::Error>> {
    let root = BitMapBackend::new(filename, (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let num_drones = strategy_history[0].len();
    let max_time = strategy_history.len();

    let mut chart = ChartBuilder::on(&root)
        .caption("Drone Task Allocation Evolution", ("sans-serif", 20))
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..max_time, 0.0..1.0)?;

    chart.configure_mesh().draw()?;

    for drone in 0..num_drones {
        let series = strategy_history
            .iter()
            .enumerate()
            .map(|(t, strategies)| (t, strategies[drone]));
        chart
            .draw_series(LineSeries::new(series, &Palette99::pick(drone)))
            .unwrap()
            .label(format!("Drone {}", drone + 1));
    }

    chart.configure_series_labels().draw()?;

    Ok(())
}

fn main() -> Result<(), Box<dyn std::error::Error>> {
    simulate_drone_swarm_evolution()?;
    Ok(())
}

The DroneSwarm struct encapsulates the drone swarm's reward structure, where each drone's task reward is predefined. The allocate_tasks method computes the total reward based on the swarm's current task allocation strategies. Strategies are dynamically updated using the update_strategies method, which introduces stochastic noise and adjusts strategies proportionally to the total reward. The simulation iterates through multiple rounds, updating and recording the strategies at each step. Finally, the visualize_strategy_evolution function leverages the plotters crate to generate a chart that depicts how the swarm's task allocation evolves, showing the emergence of cooperative or competitive behaviors among drones.

In summary, game-theoretic MARL models are essential for tackling real-world challenges in autonomous systems, resource optimization, and critical infrastructure. By integrating advanced mathematical formulations, distributed computation frameworks, and Rust’s performance-oriented capabilities, this chapter demonstrates how MARL can drive innovation in diverse domains. The provided implementations highlight practical approaches to achieving scalability, robustness, and ethical considerations in deploying MARL at scale.

12.7. Conclusion link

In this chapter, we bridged the gap between game theory and MARL, demonstrating how these two fields complement each other to model and solve multi-agent interaction problems. By leveraging the mathematical foundations of equilibria, cooperation, and competition, and implementing these concepts practically in Rust, we explored how agents can learn to make strategic decisions in both simulated and real-world environments. The integration of game theory into MARL opens pathways to innovative applications across industries, emphasizing the importance of collaboration and competition in achieving intelligent, adaptive systems.

12.7.1. Further Learning with GenAI link

Let these prompts inspire you to explore the intersections of game theory and MARL, blending rigorous theory with practical implementation to build intelligent, adaptive, and strategic multi-agent systems using Rust.

• Explain the foundational principles of game theory in MARL. How do concepts like Nash Equilibrium, Pareto Efficiency, and utility functions define multi-agent interactions? Implement a simple normal-form game in Rust, demonstrating agent strategy optimization.

• Discuss the role of payoff matrices in game-theoretic MARL. How do they capture agent rewards and decision-making strategies? Implement a payoff matrix generator in Rust and analyze agent behaviors based on different reward structures.

• Explore cooperative game theory in MARL. How does joint utility optimization enable agents to collaborate effectively? Implement a cooperative MARL task in Rust using value decomposition techniques.

• Examine coalition formation in cooperative MARL. How can agents dynamically form coalitions to maximize shared rewards? Implement coalition-based decision-making in Rust and evaluate the fairness of reward distribution using Shapley values.

• Analyze the application of Nash Equilibrium in competitive MARL. How does it guide agent strategies in non-cooperative environments? Implement Nash Equilibrium computations in Rust for a zero-sum game scenario.

• Explore mixed-strategy equilibria in MARL. How do probabilistic strategies enhance decision-making in uncertain environments? Simulate mixed-strategy equilibria in Rust and compare their performance to deterministic strategies.

• Discuss the role of correlated equilibria in MARL. How do agents coordinate using signals to achieve better outcomes? Implement signal-based coordination for correlated equilibria in Rust.

• Examine the dynamics of evolutionary game theory in MARL. How do strategies evolve over time in multi-agent populations? Implement replicator dynamics in Rust and analyze the stability of strategies.

• Explore the concept of Evolutionarily Stable Strategies (ESS). How do ESS provide robustness in agent populations? Simulate strategy evolution in Rust and identify ESS for various MARL tasks.

• Analyze the use of self-play in competitive MARL. How do agents improve through adversarial learning and repeated interactions? Implement self-play training in Rust and observe the emergence of advanced strategies.

• Discuss the significance of fairness metrics in cooperative MARL. How do Shapley values ensure equitable reward distribution among agents? Implement fairness metrics in Rust and evaluate their impact on agent cooperation.

• Examine the challenges of scaling game-theoretic MARL. What techniques can manage large-scale agent interactions effectively? Implement a large-scale MARL system in Rust and analyze its scalability and efficiency.

• Explore the application of game theory in autonomous systems. How can game-theoretic MARL improve coordination in self-driving cars or drones? Implement a drone swarm optimization task in Rust using cooperative game theory.

• Discuss the integration of game theory with deep reinforcement learning in MARL. How can deep learning enhance strategic decision-making? Implement a deep MARL framework in Rust combining game theory and policy optimization.

• Examine the role of reward shaping in game-theoretic MARL. How does it influence agent strategies and outcomes? Implement reward shaping techniques in Rust and analyze their effects on cooperation and competition.

• Analyze the trade-offs between cooperative and competitive strategies in MARL. How do hybrid systems balance these dynamics? Simulate a mixed-strategy MARL environment in Rust and evaluate agent performance under different settings.

• Explore the impact of incomplete information in MARL. How do agents strategize under uncertainty using Bayesian games? Implement a Bayesian MARL system in Rust and test its robustness to missing information.

• Discuss the ethical considerations of game-theoretic MARL. How can fairness, transparency, and accountability be ensured in real-world applications? Implement ethical safeguards in Rust for a MARL system addressing resource allocation.

• Examine the future trends in game-theoretic MARL research. How do advanced concepts like meta-learning and hierarchical equilibria shape the field? Implement a meta-learning-based MARL framework in Rust for a dynamic task environment.

• Analyze the role of transfer learning in game-theoretic MARL. How can pre-trained strategies accelerate learning in new multi-agent scenarios? Implement transfer learning techniques in Rust and evaluate their effectiveness in a real-world MARL task.

These prompts are designed to deepen your understanding of game theory's role in MARL and to help you master the art of implementing intelligent, strategic multi-agent systems using Rust.

12.7.2. Hands On Practices link

These exercises encourage hands-on experimentation and critical engagement with MARL concepts, allowing readers to apply their knowledge practically and explore real-world scenarios.

Exercise 12.1: Implementing Normal-Form and Extensive-Form Games link

Task:\ Develop a Rust-based implementation of both normal-form and extensive-form games. Simulate a multi-agent scenario where agents optimize their strategies based on Nash Equilibrium.

Challenge:\ Experiment with different payoff structures (e.g., zero-sum vs. non-zero-sum games) and analyze the impact on agent strategies and equilibria. Extend the implementation to dynamic games with repeated interactions, observing how agent strategies evolve over time.

Exercise 12.2: Cooperative Policy Learning in MARL link

Task:\ Create a cooperative MARL task in Rust where agents work together to maximize a joint reward. Use value decomposition techniques to learn shared policies.

Challenge:\ Implement a fairness metric (e.g., Shapley values) to redistribute rewards equitably among agents. Experiment with scenarios where some agents act selfishly and analyze the system’s stability and performance under varying cooperation levels.

Exercise 12.3: Simulating Competitive MARL Using Zero-Sum Games link

Task:\ Implement a competitive multi-agent task in Rust, such as an adversarial pursuit-evasion game, using zero-sum game principles. Model agent strategies using Nash Equilibrium.

Challenge:\ Introduce probabilistic strategies (mixed strategies) for agents and compare their performance against deterministic approaches. Evaluate the effectiveness of self-play in training robust adversarial agents.

Exercise 12.4: Evolutionary Strategy Development in MARL link

Task:\ Simulate evolutionary dynamics in Rust for a population of agents competing in a shared environment. Implement replicator equations to model the evolution of agent strategies over time.

Challenge:\ Analyze the convergence to Evolutionarily Stable Strategies (ESS) under different initial conditions. Experiment with adding noise to the system and evaluate the robustness of the evolutionary process.

Exercise 12.5: Real-World Application of Game-Theoretic MARL link

Task:\ Design a MARL system in Rust for a real-world application, such as traffic management, energy market optimization, or autonomous vehicle coordination. Integrate game-theoretic principles to guide agent interactions.

Challenge:\ Incorporate constraints like fairness, resource limitations, and ethical considerations into the system. Compare the effectiveness of cooperative and competitive strategies in achieving system-wide objectives.

By engaging with these exercises, you will gain practical experience in building advanced MARL systems, experiment with key game-theoretic principles, and explore real-world applications using Rust. These carefully selected exercises emphasize strategic decision-making, scalability, and fairness.