15.1. Introduction to Deep Learning link

The integration of deep learning into reinforcement learning (RL) represents a pivotal evolution in AI, merging two once-distinct paradigms to tackle increasingly complex decision-making problems. The historical roots of this synthesis trace back to the limitations of traditional RL methods, which relied on manually engineered features or tabular representations to approximate value functions and policies. While effective in simpler, low-dimensional tasks, these approaches struggled to scale to environments rich with high-dimensional data, such as raw images, audio signals, or text.

Deep learning offered a solution by automating feature extraction and learning directly from unstructured data. Inspired by the brain's structure and functionality, deep neural networks excelled in capturing intricate patterns and representations, enabling RL agents to perceive and act within environments that were once beyond their reach. The breakthrough moment came with the advent of Deep Q-Networks (DQN) by DeepMind in 2013, which demonstrated that deep neural networks could approximate value functions effectively, allowing agents to play Atari games directly from raw pixel inputs. This achievement marked a paradigm shift, showcasing the potential of deep reinforcement learning (DRL) to solve tasks where explicit modeling or feature engineering was impractical.

Motivationally, the integration of deep learning into RL was driven by the desire to create more generalizable and scalable agents. Traditional AI systems often relied on narrow, domain-specific rules that limited their applicability. Researchers aimed to bridge this gap by developing agents capable of learning directly from experience in diverse environments, adapting autonomously to new challenges. This aspiration aligned with broader goals in AI to emulate human-like intelligence, where learning and decision-making are inherently flexible and scalable across various domains.

Moreover, the rise of computational power and access to large-scale datasets in the early 2010s provided fertile ground for this integration. GPUs enabled the efficient training of deep neural networks, while advancements in optimization techniques and frameworks lowered the barriers to implementation. These technological developments, combined with the growing ambition to tackle real-world challenges like robotics, autonomous vehicles, and resource management, fueled the motivation to embed deep learning within RL.

Today, DRL stands as a cornerstone in AI, pushing the boundaries of what machines can achieve. By equipping RL agents with the ability to learn from complex, high-dimensional inputs, deep learning has unlocked the potential for breakthroughs across industries, transforming abstract academic concepts into tangible, impactful solutions.

A deep neural network can be mathematically represented as a composition of functions, each corresponding to a layer in the network:

$$ f_\theta(x) = f_L \circ f_{L-1} \circ \cdots \circ f_1(x), $$

where $f_i(x)$ represents the transformation applied at the $i$-th layer, parameterized by weights $W_i$ and biases $b_i$. Each layer performs a linear transformation followed by a non-linear activation function:

$$ f_i(x) = \sigma(W_i x + b_i), $$

with $\sigma$ being an activation function such as ReLU, Sigmoid, or Tanh. These non-linear activations are essential as they allow the network to model complex, non-linear relationships between inputs and outputs. The universal approximation theorem assures us that neural networks can approximate any continuous function to an arbitrary degree of accuracy, given sufficient depth and appropriate activation functions.

The Tensorflow playground illustrates the core structure and functioning of a basic deep neural network as it processes a classification problem. Each hidden layer in the network corresponds to a transformation $f_i(x) = \sigma(W_i x + b_i)$, where the weights $W_i$ and biases $b_i$ are adjusted during training to minimize the loss function. The use of an activation function, such as the Tanh shown in the image, introduces non-linearity into the transformations, enabling the network to model complex patterns, like the spirals in the dataset. This step-by-step transformation of inputs $x_1$ and $x_2$ through successive hidden layers showcases how the network builds hierarchical representations, from raw input features to a refined understanding of the underlying data distribution.

The visualization from playground also highlights the critical role of network depth in capturing intricate relationships. With six hidden layers, the network gains sufficient capacity to approximate the non-linear decision boundary that separates the two classes in the spiral dataset, as predicted by the universal approximation theorem. The weights connecting the neurons are depicted with varying thickness, representing their magnitude and contribution to the output, while the color coding reflects the activation values. This clear depiction of feature transformations through hidden layers effectively demonstrates how deep learning leverages composition to extract meaningful patterns from raw data.

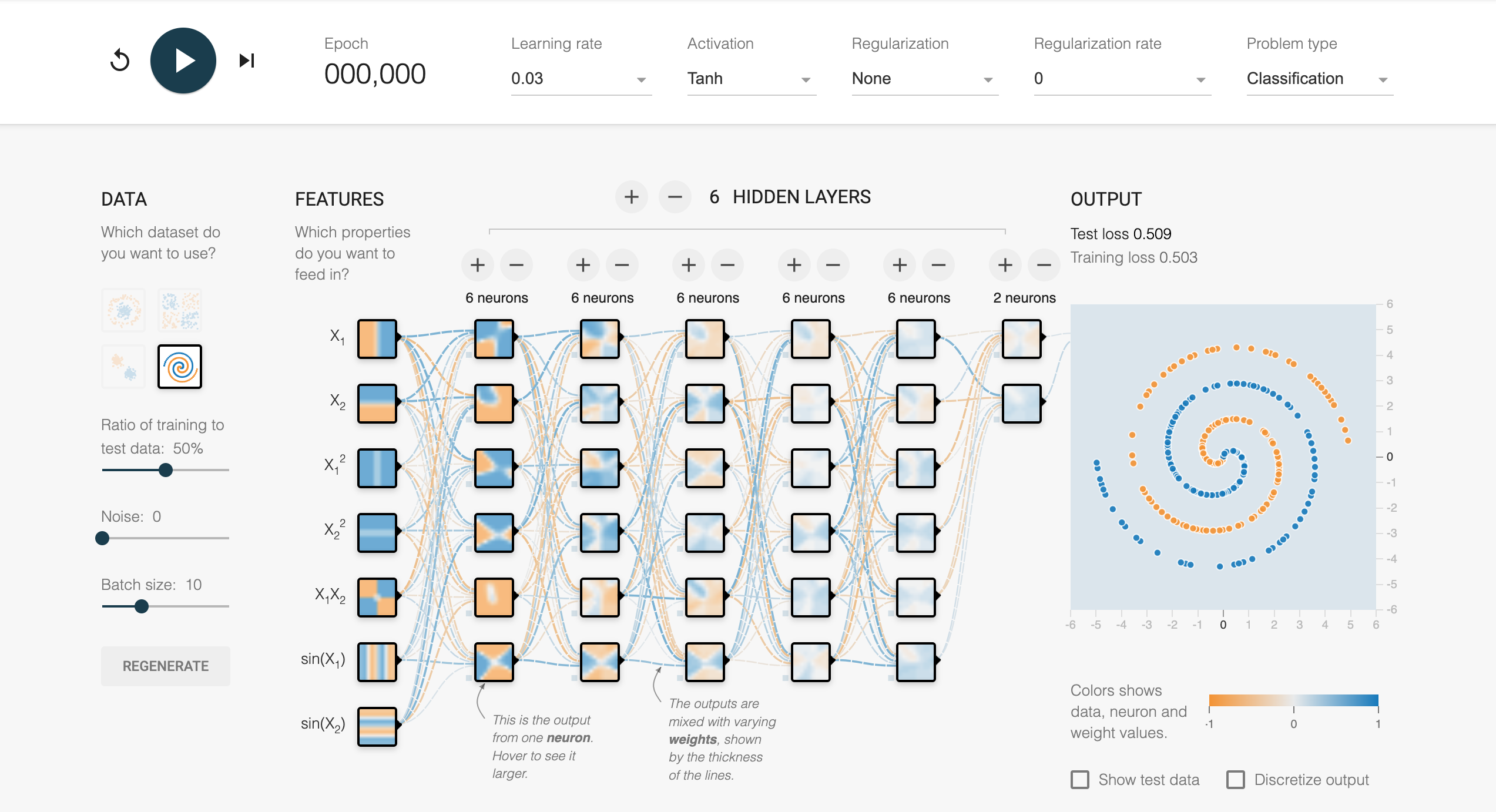
Figure 1: Illustration of deep learning from Tensorflow Playground (Ref: https://playground.tensorflow.org).

Training these networks involves optimizing the parameters $\theta = \{W_i, b_i\}$ to minimize a loss function $L(\theta)$, which quantifies the discrepancy between the network's predictions and the actual targets. The optimization process leverages the backpropagation algorithm, which efficiently computes the gradients of the loss function with respect to each parameter using the chain rule:

$$ \frac{\partial L}{\partial \theta_i} = \frac{\partial L}{\partial f_i} \cdot \frac{\partial f_i}{\partial \theta_i}. $$

These gradients are then used to update the parameters in the direction that minimizes the loss, typically using gradient descent or one of its variants:

$$ \theta_{t+1} = \theta_t - \alpha \nabla_\theta L, $$

where $\alpha$ is the learning rate, and $\nabla_\theta L$ denotes the gradient of the loss with respect to the parameters. This iterative process allows for the effective training of networks with millions or even billions of parameters.

In the realm of reinforcement learning, deep learning techniques are instrumental in approximating complex functions that are infeasible to model directly. Specifically, neural networks are employed to approximate policies and value functions, which are central to RL algorithms.

• Policy-Based Methods: Neural networks parameterize the policy $\pi(a|s)$, mapping states $s$ to a probability distribution over actions $a$. This enables agents to learn stochastic policies that can handle the exploration-exploitation trade-off inherent in RL.

• Value-Based Methods: Neural networks estimate the value function $V(s)$ or the action-value function $Q(s, a)$, representing the expected cumulative reward from a state or state-action pair. For instance, Deep Q-Networks (DQNs) use convolutional neural networks to approximate $Q(s, a)$ in environments with visual inputs, like Atari games, allowing agents to learn directly from raw pixel data.

• Actor-Critic Methods: These combine policy-based and value-based approaches by simultaneously learning a policy (actor) and a value function (critic), often sharing parameters within a single network architecture.

The integration of deep learning into RL addresses the limitations of traditional machine learning methods, which often rely on manual feature engineering and struggle with high-dimensional or unstructured data. Deep neural networks automatically learn hierarchical feature representations from raw inputs, enabling RL agents to process complex sensory data without explicit feature extraction. This capability is particularly beneficial in environments where the state space is vast or continuous.

The depth of a neural network is crucial for its ability to capture intricate patterns and dependencies in data. Deeper networks can represent more complex functions by composing multiple layers of non-linear transformations. This hierarchical feature extraction allows lower layers to detect simple patterns, such as edges in images, while higher layers capture more abstract concepts, like objects or even actions.

However, training deep networks comes with challenges, such as vanishing or exploding gradients, which can hinder the optimization process. Techniques like normalization layers, residual connections, and advanced optimization algorithms have been developed to mitigate these issues, facilitating the training of very deep networks.

Deep learning has revolutionized reinforcement learning (RL) by addressing challenges in advanced applications, starting with partial observability. In many real-world environments, agents cannot perceive the complete state of the environment at every step. Here, recurrent neural networks (RNNs) and Long Short-Term Memory (LSTM) networks come into play, maintaining a hidden state that summarizes information over time. This capability enables agents to infer crucial details about the environment’s dynamics from past observations, allowing them to make informed decisions even with limited or noisy input. For instance, an LSTM-based RL agent in a partially observable robotics task can remember prior sensor readings to navigate effectively in unseen terrains, exemplifying how deep learning extends RL's capabilities in complex scenarios.

In environments with continuous action spaces, where discrete actions like "move left" or "move right" are insufficient, deep learning offers powerful tools. Methods like Deep Deterministic Policy Gradients (DDPG) and other actor-critic algorithms utilize neural networks to generate smooth, continuous action outputs directly. These approaches allow RL agents to perform fine-grained control in tasks like robotic manipulation or autonomous driving. Additionally, deep learning enhances RL in multi-agent systems, where multiple agents interact in shared environments, often with conflicting goals. Neural networks approximate the policies and value functions for each agent, efficiently managing the combinatorial explosion of possible interactions. Finally, deep learning drives innovations in transfer learning and meta-learning within RL, enabling agents to generalize across tasks by leveraging shared representations. By learning to learn, agents can adapt quickly to new challenges, reducing training time and enhancing performance in diverse applications, from gaming to real-world decision-making.

Nowadays, deep learning has become an indispensable component of modern reinforcement learning, providing the computational machinery necessary to handle the complexities of real-world environments. By leveraging the hierarchical learning capabilities of deep neural networks, RL agents can learn effective policies and value functions directly from raw, high-dimensional data. This synergy between deep learning and reinforcement learning continues to drive advancements in artificial intelligence, enabling the development of agents capable of sophisticated decision-making and problem-solving in diverse domains.

Practically, implementing deep learning in Rust for RL applications involves structuring neural networks as modular and efficient systems. Rust's type safety, performance, and memory management make it a powerful choice for building RL agents. AI engineers can define layers as structs, encapsulating weights, biases, and activation functions as properties, and implement forward passes as methods. Libraries like ndarray and tch-rs provide robust support for matrix operations and tensor computations, enabling seamless integration of linear transformations and activation functions. By leveraging Rust's features, RL practitioners can create scalable, high-performance neural networks that handle the complexities of modern reinforcement learning environments effectively. This integration of foundational concepts with Rust’s practical capabilities ensures the development of RL systems that are both robust and efficient.

This Rust program implements a simple feedforward neural network using the tch library for training a multi-layer perceptron (MLP) to classify synthetic 2D circular data points into two categories. The program generates a dataset with circular patterns, builds an MLP with six layers (five hidden layers and one output layer), trains it using the Adam optimizer, and visualizes the decision boundary and classified points. Gradients and predictions during forward and backward propagation are logged to demonstrate the learning process.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use plotters::prelude::*;
use rand::Rng;
use tch::{nn, nn::OptimizerConfig, Device, Kind, Tensor};
use tch::nn::ModuleT;

fn main() -> anyhow::Result<()> {
    // 1. Generate 2D synthetic datasets with circular pattern
    let n_samples = 1000;
    let mut rng = rand::thread_rng();
    let mut data = Vec::new();
    let mut labels = Vec::new();

    for _ in 0..n_samples {
        let r = rng.gen_range(0.0..2.0);
        let theta = rng.gen_range(0.0..(2.0 * std::f64::consts::PI));
        let x = r * theta.cos();
        let y = r * theta.sin();
        data.push([x, y]);
        labels.push(if r < 1.0 { 0 } else { 1 });
    }

    let data: Tensor = Tensor::of_slice2(&data)
        .to_kind(Kind::Float)
        .to_device(Device::Cpu);
    let labels: Tensor = Tensor::of_slice(&labels)
        .to_kind(Kind::Int64)
        .to_device(Device::Cpu);

    // 2. Define Multi-Layer Perceptron with 6 hidden layers (8 neurons each)
    let vs = nn::VarStore::new(Device::Cpu);
    let net = nn::seq()
        .add(nn::linear(&vs.root(), 2, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&vs.root(), 8, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&vs.root(), 8, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&vs.root(), 8, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&vs.root(), 8, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&vs.root(), 8, 2, Default::default()));

    // 3. Train the model using Adam optimizer
    let mut opt = nn::Adam::default().build(&vs, 1e-3).unwrap();

    for epoch in 1..=500 {
        // Forward pass
        let preds = net.forward_t(&data, true);
        
        // Log forward pass output for the first batch
        if epoch == 1 || epoch % 100 == 0 {
            println!("Epoch {} - Forward pass output (first 5 samples): {:?}", epoch, preds.narrow(0, 0, 5));
        }
        
        // Compute loss
        let loss = preds.cross_entropy_for_logits(&labels);
        
        // Backward pass
        opt.zero_grad();
        loss.backward();
        
        // Optimizer step
        opt.step();

        if epoch % 50 == 0 {
            println!("Epoch: {}, Loss: {:.4}", epoch, loss.double_value(&[]));
        }
    }

    // 4. Evaluate and visualize the results
    let preds = net.forward_t(&data, false).argmax(1, false);
    let accuracy = preds.eq_tensor(&labels).to_kind(Kind::Float).mean(Kind::Float);
    println!("Accuracy: {:.2}%", accuracy.double_value(&[]) * 100.0);

    // Visualization setup
    let root = BitMapBackend::new("classification_visualization.png", (800, 800)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .margin(5)
        .caption("MLP Classification and Predictions", ("sans-serif", 30))
        .x_label_area_size(30)
        .y_label_area_size(30)
        .build_cartesian_2d(-2.5..2.5, -2.5..2.5)?;

    chart.configure_mesh().draw()?;

    // Plot decision boundary
    let resolution = 200;
    let mut grid_data = vec![];
    for i in 0..resolution {
        for j in 0..resolution {
            let x = -2.5 + 5.0 * (i as f64) / (resolution as f64);
            let y = -2.5 + 5.0 * (j as f64) / (resolution as f64);
            grid_data.push([x, y]);
        }
    }

    let grid_tensor: Tensor = Tensor::of_slice2(&grid_data)
        .to_kind(Kind::Float)
        .to_device(Device::Cpu);
    let grid_preds = net.forward_t(&grid_tensor, false).argmax(1, false);

    let grid_points: Vec<(f64, f64, u8)> = grid_data
        .iter()
        .zip(grid_preds.iter::<i64>().unwrap())
        .map(|(coords, label)| (coords[0], coords[1], label as u8))
        .collect();

    chart.draw_series(
        grid_points.iter().map(|(x, y, label)| {
            let color = if *label == 0 { &BLUE.mix(0.2) } else { &RED.mix(0.2) };
            Circle::new((*x, *y), 1, color.filled())
        }),
    )?;

    // Plot original data points
    let data_points: Vec<((f64, f64), i64)> = data
        .to_kind(Kind::Double)
        .chunk(2, 1)
        .iter()
        .zip(labels.iter::<i64>().unwrap())
        .map(|(coords, label)| {
            let x = coords.double_value(&[0]);
            let y = coords.double_value(&[1]);
            ((x, y), label)
        })
        .collect();

    chart.draw_series(
        data_points
            .iter()
            .filter(|(_, label)| *label == 0)
            .map(|((x, y), _)| Circle::new((*x, *y), 3, BLUE.filled())),
    )?;

    chart.draw_series(
        data_points
            .iter()
            .filter(|(_, label)| *label == 1)
            .map(|((x, y), _)| Circle::new((*x, *y), 3, RED.filled())),
    )?;

    root.present()?;
    println!("Visualization saved to classification_visualization.png");

    Ok(())
}

The program begins by generating a synthetic dataset with 2D points arranged in concentric circles, assigning labels based on the radius. It then constructs an MLP with ReLU activation for hidden layers and a linear transformation for the output layer. During training, the network performs forward propagation to compute predictions, calculates the cross-entropy loss, and applies backward propagation to update the model’s weights using gradients. Logging mechanisms provide insights into the forward outputs, loss values, and gradient updates for specific layers. After training, the network's decision boundary and predictions are visualized to evaluate performance.

Forward propagation involves passing input data through the neural network to compute output predictions. Each layer applies a linear transformation followed by a non-linear activation (e.g., ReLU), propagating information from input to output. Backward propagation, or backprop, calculates gradients of the loss function with respect to model parameters using the chain rule. These gradients indicate how each parameter contributes to the error, enabling the optimizer (Adam in this case) to adjust weights and biases in the direction that minimizes the loss. Together, forward and backward propagation iteratively refine the model's parameters to improve performance on the classification task.

By running this example, you can observe the network's ability to learn the target value function through gradient-based optimization, illustrating the principles of forward and backward propagation in a deep learning system tailored for reinforcement learning tasks.

15.2. Linear and Nonlinear Transformations link

In the realm of reinforcement learning (RL), neural networks serve as versatile tools for approximating complex functions, enabling agents to make decisions in dynamic and high-dimensional environments. These networks fundamentally operate by processing inputs through a series of layers, where each layer applies transformations that extract and refine meaningful features. At their core, neural networks leverage two key operations: linear transformations and nonlinear activation functions. These operations work in tandem, allowing the network to represent intricate relationships and capture the underlying structure of data.

Linear transformations form the backbone of neural networks, where inputs are multiplied by weights and combined with biases. This operation enables the network to compute weighted sums of inputs, effectively projecting data into different spaces. However, linear transformations alone are insufficient for capturing complex, nonlinear patterns in data. This is where nonlinear activation functions become essential. Activation functions, such as ReLU, Sigmoid, and Tanh, introduce nonlinearity to the network, allowing it to model intricate dependencies and decision boundaries. Nonlinearities enable neural networks to approximate complex functions and relationships, making them capable of solving tasks ranging from image recognition to strategic decision-making in RL.

A linear transformation is a fundamental mathematical operation that maps an input vector $\mathbf{x} \in \mathbb{R}^n$ to an output vector $\mathbf{y} \in \mathbb{R}^m$ using a weight matrix $\mathbf{W} \in \mathbb{R}^{m \times n}$ and a bias vector $\mathbf{b} \in \mathbb{R}^m$:

$$ \mathbf{y} = \mathbf{W}\mathbf{x} + \mathbf{b}. $$

In this equation, the matrix $\mathbf{W}$ defines how each input feature contributes to each output feature, while the bias vector $\mathbf{b}$ allows for shifting the transformation, providing the network with additional flexibility. Linear transformations serve as the building blocks of neural networks, forming the connections between layers. In the context of RL, these transformations help map states to actions or value estimates, facilitating the agent's understanding of the environment. For instance, in policy networks, linear layers can map high-dimensional state representations to action probabilities.

Despite their fundamental role, linear transformations have inherent limitations in expressive power. Stacking multiple linear layers without any nonlinearity results in another linear transformation. Mathematically, if we have two linear transformations $\mathbf{y} = \mathbf{W}_2 (\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) + \mathbf{b}_2$, this can be simplified to a single linear transformation $\mathbf{y} = \mathbf{W}' \mathbf{x} + \mathbf{b}$, where $\mathbf{W}' = \mathbf{W}_2 \mathbf{W}_1$ and $\mathbf{b}' = \mathbf{W}_2 \mathbf{b}_1 + \mathbf{b}_2$. This linearity restricts the network's ability to model complex, nonlinear relationships present in RL tasks, such as interactions between different state variables or non-additive reward structures.

To overcome the limitations of linear transformations, neural networks incorporate nonlinear activation functions applied element-wise to the outputs of linear layers. These nonlinearities introduce the necessary complexity, enabling networks to model intricate functions and decision boundaries. The significance of nonlinear activation functions is underscored by the Universal Approximation Theorem (UAT), which states that a feedforward neural network with at least one hidden layer containing a finite number of neurons and a suitable nonlinear activation function can approximate any continuous function on a compact subset of $\mathbb{R}^n$ to any desired degree of accuracy. This theorem provides the theoretical foundation for using neural networks as universal function approximators in RL.

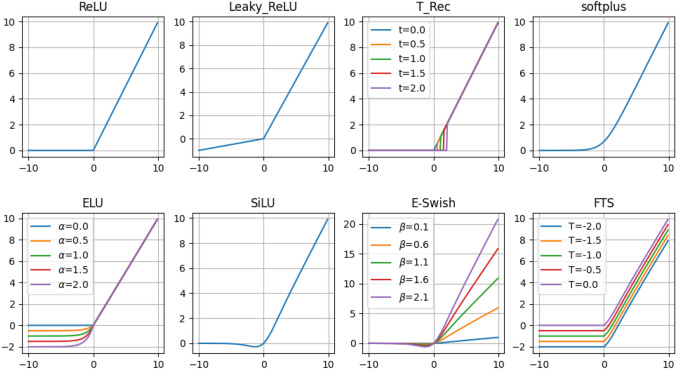
Figure 2: Commonly used activation functions for deep learning.

Among the most common activation functions is the Rectified Linear Unit (ReLU), defined as:

$$ \text{ReLU}(x) = \max(0, x). $$

ReLU is computationally efficient and mitigates the vanishing gradient problem by providing a constant gradient for positive inputs. It is widely used in deep RL architectures due to its simplicity and effectiveness, particularly in convolutional neural networks processing visual inputs.

Another fundamental activation function is the sigmoid function $\sigma(x) = \frac{1}{1 + e^{-x}}$, which outputs values in the range (0, 1), making it suitable for modeling probabilities. However, it is prone to vanishing gradients for large positive or negative inputs, which can slow down learning. In RL, the sigmoid function is commonly used in the output layer when modeling binary actions or probabilities.

The hyperbolic tangent function (tanh) is also widely used, defined as:

$$ \tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}. $$

Tanh centers data around zero and outputs values in the range (-1, 1), which can be beneficial in hidden layers where centered data improves convergence. However, like the sigmoid function, tanh can suffer from vanishing gradients, especially for inputs far from zero.

Modern deep learning introduces advanced activation functions to address the shortcomings of traditional functions, particularly in the context of deep RL. The Leaky ReLU is one such function, defined as:

$$ \text{LeakyReLU}(x) = \begin{cases} x, & \text{if } x > 0, \\ \alpha x, & \text{otherwise}, \end{cases} $$

where $\alpha$ is a small constant, typically 0.01. Leaky ReLU allows a small, non-zero gradient when the unit is not active (i.e., $x < 0$), preventing "dead" neurons and enhancing the learning capacity in networks where negative inputs are significant.

The Exponential Linear Unit (ELU) is another advanced activation function, given by:

$$ \text{ELU}(x) = \begin{cases} x, & \text{if } x \geq 0, \\ \alpha (e^{x} - 1), & \text{if } x < 0, \end{cases} $$

where $\alpha$ is a positive constant. ELU improves learning by bringing mean activations closer to zero and reduces computational complexity. In RL, it is beneficial in deep networks where faster convergence is desired.

The Swish function is defined as:

$$ \text{Swish}(x) = x \cdot \sigma(x), $$

and has been shown to outperform ReLU in deep networks by providing better gradient flow. It enhances performance in policy and value networks by allowing smoother transitions between activated and non-activated states.

The Gaussian Error Linear Unit (GELU) is another activation function, defined as:

$$ \text{GELU}(x) = x \cdot \Phi(x), $$

where $\Phi(x)$ is the cumulative distribution function of the standard normal distribution. GELU applies a smooth gating mechanism, enabling networks to capture complex patterns. It is particularly useful in transformer architectures and advanced RL models requiring sophisticated function approximation.

The Universal Approximation Theorem (UAT) s a foundational result in neural network theory that demonstrates the expressive power of feedforward neural networks. Formally, it states that a feedforward network with at least one hidden layer, a finite number of neurons, and a suitable nonlinear activation function can approximate any continuous function $f$ defined on a compact subset $K \subseteq \mathbb{R}^n$ to any desired degree of accuracy. This result highlights the theoretical capability of neural networks to serve as universal function approximators.

Mathematically, the theorem asserts that for any continuous function $f: K \to \mathbb{R}$ and any $\varepsilon > 0$, there exists a neural network $\phi(x)$ such that:

$$ \sup_{x \in K} \left| f(x) - \phi(x) \right| < \varepsilon,x∈K $$

where $\phi(x)$ is the output of the neural network. The network represents $\phi(x)$ as a sum of weighted activation functions applied to linear combinations of inputs:

$$ \phi(x) = \sum_{i=1}^M c_i \, \sigma \left( w_i^T x + b_i \right). $$

Here, $M$ is the number of neurons in the hidden layer, $c_i \in \mathbb{R}$ are the output weights, $w_i \in \mathbb{R}^n$ and $b_i \in \mathbb{R}$ are the input weights and biases, and $\sigma: \mathbb{R} \to \mathbb{R}$ is the nonlinear activation function. The choice of activation function $\sigma$ is critical; it must be nonlinear (e.g., sigmoid, hyperbolic tangent, or ReLU) to ensure the network's ability to approximate complex functions.

The theorem guarantees that such a neural network can approximate $f(x)$ on $K$ with finite neurons, but it does not provide explicit bounds on the number of neurons or layers required to achieve a specific accuracy $\varepsilon$. Additionally, the approximation is valid only for continuous functions over compact subsets, meaning extensions are needed for discontinuous functions or non-compact domains.

The UAT is particularly significant in the context of reinforcement learning (RL), where agents learn to make sequences of decisions to maximize cumulative rewards. RL environments often feature stochastic and nonlinear dynamics, with complex state-action-reward relationships. Neural networks with nonlinear activation functions are crucial for modeling these complexities effectively, enabling agents to approximate value functions and policies that drive optimal decision-making.

Nonlinearity is indispensable for capturing intricate dependencies in RL. For example, optimal policies and value functions in RL are rarely linear in the state space; they often require the representation of sharp changes or steep gradients in response to critical state transitions. Nonlinear activation functions allow neural networks to approximate these relationships, ensuring that the expected return can be estimated accurately. Without nonlinearity, linear models would fail to capture the richness of interactions between states and actions, leading to suboptimal policies.

In high-dimensional and continuous spaces, nonlinearities become even more critical. For RL problems involving visual inputs, such as those requiring image-based state representations, deep convolutional networks with nonlinear activation functions are essential. These networks learn hierarchical representations, progressing from low-level features like edges and textures in early layers to high-level abstractions like objects or scenes in deeper layers. Similarly, in continuous action spaces, nonlinear transformations enable the modeling of nuanced action-reward effects, allowing agents to learn precise control policies.

Linear models are fundamentally insufficient for most RL tasks, particularly in environments where rewards depend on nonlinear interactions between state variables. For instance, environments with rewards that exhibit sharp transitions or non-smooth behavior require approximations that can capture these features. Nonlinear activation functions empower neural networks to approximate such complex mappings, handling steep gradients, and interactions among state variables.

The choice of activation functions significantly impacts the performance and convergence of RL algorithms. Functions like ReLU and its variants enhance training stability by mitigating vanishing gradient problems, which is vital for stable and efficient learning. Moreover, advanced activation functions such as Swish and GELU provide smoother gradients, facilitating better gradient flow in very deep networks and improving convergence. These properties are especially important in RL, where agents often need to balance exploration and exploitation over long training horizons.

Computational efficiency is another key factor in RL applications. Simpler activation functions, like ReLU, are computationally efficient and suitable for real-time or resource-constrained scenarios. In contrast, smoother functions like Swish may offer better convergence properties in deep networks, albeit at a slight computational cost. Balancing computational overhead with expressive power is crucial, particularly in RL applications where agents must operate in real-time or handle complex, high-dimensional environments.

In summary, the UAT provides the theoretical justification for using neural networks in RL, but practical considerations—such as network architecture, activation function choice, and computational constraints—play a significant role in real-world performance. By leveraging nonlinear activation functions effectively, RL agents can approximate complex policies and value functions, enabling them to navigate and succeed in dynamic, high-dimensional environments.

Practical considerations in RL include the combination of batch normalization with certain activation functions to further improve training dynamics. Batch normalization helps in stabilizing the distribution of inputs to each layer, which can mitigate issues like internal covariate shift and improve training speed. Activation functions that affect the distribution of outputs can influence the agent's exploration strategies, impacting the balance between exploration and exploitation, a fundamental trade-off in RL.

In some RL scenarios, designing custom activation functions tailored to the problem domain can yield better performance. For instance, in domains where the agent's actions must satisfy certain constraints or where the reward landscape has specific characteristics, specialized activation functions can help the network learn more effectively.

Implementing linear and nonlinear transformations in Rust involves leveraging the language's features to achieve efficient computation. Rust's low-level control allows for optimization of matrix operations and activation function computations, which are critical in high-performance RL applications. Utilizing Rust's concurrency features can parallelize computations across CPU cores or GPU threads, enhancing performance for large-scale problems.

Safety is ensured through Rust's ownership system, preventing data races and ensuring memory safety in multi-threaded RL applications. This is particularly important in RL, where agents often need to interact with environments and process data streams concurrently.

By harnessing the power of Rust for implementing these concepts, practitioners can build robust, high-performance RL systems capable of tackling real-world challenges. Rust's strong type system and emphasis on safety without sacrificing performance make it an excellent choice for developing RL frameworks and algorithms.

Linear and nonlinear transformations are integral to the success of deep learning in reinforcement learning. Linear transformations provide the structural framework for neural networks, mapping inputs through layers of computation. Nonlinear activation functions imbue these networks with the capacity to model the complex, dynamic environments encountered in RL. Understanding the mathematical foundations and practical implications of these transformations is essential for developing efficient and effective RL agents.

As RL continues to evolve, the interplay between linear structures and nonlinear activations will remain a cornerstone of agent development and innovation. By combining these mathematical tools with the performance and safety of Rust, practitioners can push the boundaries of what RL agents can achieve, enabling them to solve increasingly sophisticated tasks across diverse domains.

To illustrate these concepts, we implement linear transformations and activation functions in Rust using the tch crate. We also visualize decision boundaries created by different activation functions to understand their behavior. The experiment in the code explores the performance and decision boundary visualization of a neural network with different activation functions: ReLU, Leaky ReLU, and ELU. The model is trained to classify a synthetic dataset with two concentric circular patterns into two categories. Each activation function affects the learning dynamics and the shape of the decision boundary, influencing the classification performance.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use plotters::prelude::*;
use rand::Rng;
use tch::{nn, nn::OptimizerConfig, Device, Kind, Tensor};
use tch::nn::ModuleT;

// Custom sequential network with configurable activation function
fn create_network(vs: &nn::VarStore, activation: &str) -> nn::Sequential {
    let root = vs.root();
    match activation {
        "relu" => nn::seq()
            .add(nn::linear(&root, 2, 8, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 8, 8, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 8, 8, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 8, 2, Default::default())),

        "leaky_relu" => nn::seq()
            .add(nn::linear(&root, 2, 8, Default::default()))
            .add_fn(|x| x.leaky_relu())
            .add(nn::linear(&root, 8, 8, Default::default()))
            .add_fn(|x| x.leaky_relu())
            .add(nn::linear(&root, 8, 8, Default::default()))
            .add_fn(|x| x.leaky_relu())
            .add(nn::linear(&root, 8, 2, Default::default())),

        "elu" => nn::seq()
            .add(nn::linear(&root, 2, 8, Default::default()))
            .add_fn(|x| x.elu())
            .add(nn::linear(&root, 8, 8, Default::default()))
            .add_fn(|x| x.elu())
            .add(nn::linear(&root, 8, 8, Default::default()))
            .add_fn(|x| x.elu())
            .add(nn::linear(&root, 8, 2, Default::default())),

        _ => panic!("Unsupported activation function"),
    }
}

// Function to generate circular dataset
fn generate_dataset(n_samples: usize) -> (Vec<[f64; 2]>, Vec<i64>) {
    let mut rng = rand::thread_rng();
    let mut data = Vec::new();
    let mut labels = Vec::new();

    for _ in 0..n_samples {
        let r = rng.gen_range(0.0..2.0);
        let theta = rng.gen_range(0.0..(2.0 * std::f64::consts::PI));
        let x = r * theta.cos();
        let y = r * theta.sin();
        data.push([x, y]);
        labels.push(if r < 1.0 { 0 } else { 1 });
    }

    (data, labels)
}

// Function to train and evaluate network
fn train_network(
    net: &nn::Sequential,
    data: &Tensor,
    labels: &Tensor,
    opt: &mut nn::Optimizer,
    epochs: usize,
) -> f64 {
    for epoch in 1..=epochs {
        // Forward pass
        let preds = net.forward_t(data, true);

        // Compute loss
        let loss = preds.cross_entropy_for_logits(labels);

        // Backward pass and optimization
        opt.backward_step(&loss);

        // Print loss every 50 epochs
        if epoch % 50 == 0 {
            println!("Epoch {}: Loss: {:.4}", epoch, loss.double_value(&[]));
        }
    }

    // Compute accuracy
    let preds = net.forward_t(data, false).argmax(1, false);
    let accuracy = preds.eq_tensor(labels).to_kind(Kind::Float).mean(Kind::Float);
    accuracy.double_value(&[]) * 100.0
}

// Function to visualize decision boundaries
fn visualize_decision_boundary(
    net: &nn::Sequential,
    activation: &str,
    accuracy: f64,
) -> Result<(), Box<dyn std::error::Error>> {
    // Fix: Create a variable for the filename
    let filename = format!("{}_classification.png", activation);
    let root = BitMapBackend::new(&filename, (800, 800)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .margin(5)
        .caption(
            format!("{} Activation (Accuracy: {:.2}%)", activation.to_uppercase(), accuracy),
            ("sans-serif", 30),
        )
        .x_label_area_size(30)
        .y_label_area_size(30)
        .build_cartesian_2d(-2.5..2.5, -2.5..2.5)?;

    chart.configure_mesh().draw()?;

    // Plot decision boundary
    let resolution = 200;
    let mut grid_data = vec![];
    for i in 0..resolution {
        for j in 0..resolution {
            let x = -2.5 + 5.0 * (i as f64) / (resolution as f64);
            let y = -2.5 + 5.0 * (j as f64) / (resolution as f64);
            grid_data.push([x, y]);
        }
    }

    let grid_tensor: Tensor = Tensor::of_slice2(&grid_data)
        .to_kind(Kind::Float)
        .to_device(Device::Cpu);
    let grid_preds = net.forward_t(&grid_tensor, false).argmax(1, false);

    let grid_points: Vec<(f64, f64, u8)> = grid_data
        .iter()
        .zip(grid_preds.iter::<i64>().unwrap())
        .map(|(coords, label)| (coords[0], coords[1], label as u8))
        .collect();

    // Draw decision boundary
    chart.draw_series(
        grid_points.iter().map(|(x, y, label)| {
            let color = if *label == 0 { &BLUE.mix(0.2) } else { &RED.mix(0.2) };
            Circle::new((*x, *y), 1, color.filled())
        }),
    )?;

    // Draw original data points
    let (data, labels) = generate_dataset(1000);
    let data_tensor: Tensor = Tensor::of_slice2(&data)
        .to_kind(Kind::Float)
        .to_device(Device::Cpu);
    let labels_tensor: Tensor = Tensor::of_slice(&labels)
        .to_kind(Kind::Int64)
        .to_device(Device::Cpu);

    let data_points: Vec<((f64, f64), i64)> = data_tensor
        .to_kind(Kind::Double)
        .chunk(2, 1)
        .iter()
        .zip(labels_tensor.iter::<i64>().unwrap())
        .map(|(coords, label)| {
            let x = coords.double_value(&[0]);
            let y = coords.double_value(&[1]);
            ((x, y), label)
        })
        .collect();

    chart.draw_series(
        data_points
            .iter()
            .filter(|(_, label)| *label == 0)
            .map(|((x, y), _)| Circle::new((*x, *y), 3, BLUE.filled())),
    )?;

    chart.draw_series(
        data_points
            .iter()
            .filter(|(_, label)| *label == 1)
            .map(|((x, y), _)| Circle::new((*x, *y), 3, RED.filled())),
    )?;

    root.present()?;
    Ok(())
}

fn main() -> Result<(), Box<dyn std::error::Error>> {
    // Set random seed for reproducibility
    tch::maybe_init_cuda();

    // Activation functions to compare
    let activations = ["relu", "leaky_relu", "elu"];

    // Generate dataset
    let (data, labels) = generate_dataset(1000);
    let data_tensor: Tensor = Tensor::of_slice2(&data)
        .to_kind(Kind::Float)
        .to_device(Device::Cpu);
    let labels_tensor: Tensor = Tensor::of_slice(&labels)
        .to_kind(Kind::Int64)
        .to_device(Device::Cpu);

    // Compare different activation functions
    for activation in &activations {
        println!("\nTraining with {} activation", activation);

        // Create VarStore and network
        let vs = nn::VarStore::new(Device::Cpu);
        let net = create_network(&vs, activation);

        // Create optimizer
        let mut opt = nn::Adam::default().build(&vs, 1e-3)?;

        // Train network
        let accuracy = train_network(&net, &data_tensor, &labels_tensor, &mut opt, 500);

        // Visualize decision boundary
        visualize_decision_boundary(&net, activation, accuracy)?;

        println!("Accuracy with {}: {:.2}%", activation, accuracy);
    }

    println!("\nDecision boundary visualizations saved!");

    Ok(())
}

The program generates a 2D dataset of points within a circular region, assigning labels based on the distance from the origin. A multi-layer perceptron (MLP) is constructed with four layers, each with eight neurons, using one of the three activation functions. The model is trained using the Adam optimizer for 500 epochs, and the resulting decision boundary is visualized for each activation function. The visualizations are saved as separate charts, each showing the model's accuracy and classification boundary.

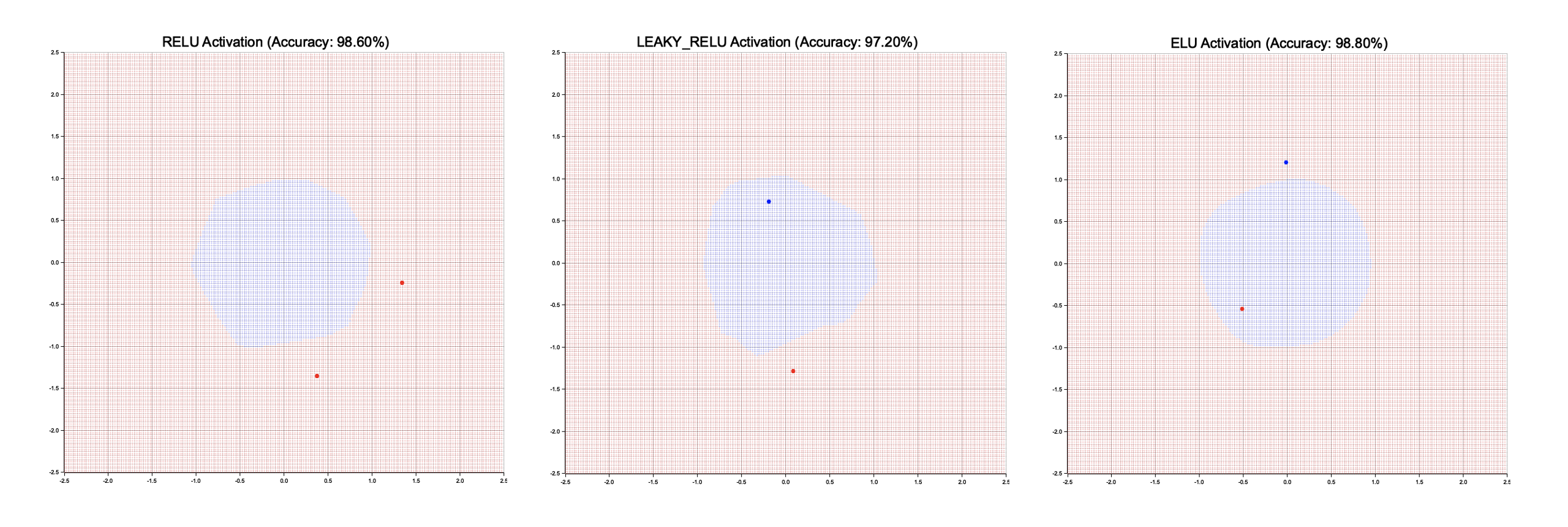
Figure 3: Plotters visualization decision boundaries of different activation functions.

The visualizations show that all three activation functions effectively classify the data, achieving high accuracy (97-99%). However, the shape and smoothness of the decision boundary vary slightly due to the different properties of the activation functions. ReLU generally produces sharp boundaries, while Leaky ReLU offers slight flexibility in negative regions, and ELU results in smoother transitions near the boundary. These differences highlight how activation functions influence the learned representation and decision-making of neural networks.

By implementing and experimenting with these transformations, readers gain insight into the critical role of non-linearity in enabling neural networks to solve reinforcement learning tasks effectively. Through practical exploration, the importance of activation functions in defining decision boundaries and optimizing network performance becomes evident.

15.3. Optimization Techniques link

Optimization is the cornerstone of training neural networks in reinforcement learning (RL), enabling agents to refine their decision-making capabilities and adapt to dynamic environments. At its essence, optimization is the iterative process through which an agent improves its neural network's parameters—its weights and biases—to better approximate policies or value functions. The goal is to minimize a loss function, which measures the discrepancy between the agent's predictions and the desired outcomes, ultimately guiding the agent toward optimal behavior.

The training process relies on gradient-based optimization methods, where gradients indicate the direction and magnitude of change required to improve the loss function. Advanced algorithms like Adam and RMSProp have become indispensable in deep RL due to their ability to adapt learning rates dynamically for each parameter. Adam, for instance, combines the advantages of momentum and adaptive learning rates, allowing for efficient convergence even in high-dimensional parameter spaces. RMSProp, on the other hand, excels in handling non-stationary objectives, which are common in RL environments where the agent's learning dynamics are constantly evolving. These optimizers provide stability and efficiency in navigating the complex, rugged landscapes of RL loss functions.

However, optimization in deep RL presents unique challenges. Unlike supervised learning, where data is independently and identically distributed, RL involves learning from sequential, correlated data generated by the agent's interactions with the environment. This introduces issues such as high variance in gradient estimates and the instability of training due to feedback loops between the agent's policy and its experience. Techniques like experience replay, which stores past interactions for sampling, and target networks, which stabilize updates, address these challenges by breaking data correlations and smoothing learning dynamics.

The cornerstone of optimization in deep learning is gradient descent, an iterative method used to minimize a loss function $L(\theta)$ with respect to the network parameters $\theta$. At each time step ttt, the parameters are updated in the opposite direction of the gradient of the loss function:

$$ \theta_{t+1} = \theta_t - \alpha \nabla_\theta L, $$

where $\alpha > 0$ is the learning rate, controlling the step size of each update, and $\nabla_\theta L$ is the gradient of the loss function with respect to $\theta$. The gradient provides the direction of the steepest ascent, so moving in the negative gradient direction leads to the steepest descent, ideally reducing the loss.

In the context of RL, calculating the full gradient over the entire dataset (full-batch gradient descent) is often impractical due to the sequential and interactive nature of data generation. Instead, stochastic gradient descent (SGD) is employed, which updates parameters using gradients computed from small, randomly sampled batches of data:

$$ \theta_{t+1} = \theta_t - \alpha \nabla_\theta L(\theta_t; \mathcal{B}_t), $$

where $\mathcal{B}_t$ is a mini-batch sampled from the data at time $t$. While SGD introduces noise into the gradient estimates, it allows for more frequent updates and can help escape local minima. However, vanilla SGD has limitations, such as sensitivity to the choice of learning rate and difficulty in navigating the noisy, non-convex loss landscapes typical in deep RL.

To overcome these challenges, advanced optimization algorithms incorporate concepts like momentum and adaptive learning rates, which are particularly beneficial in RL settings where rewards can be sparse or noisy.

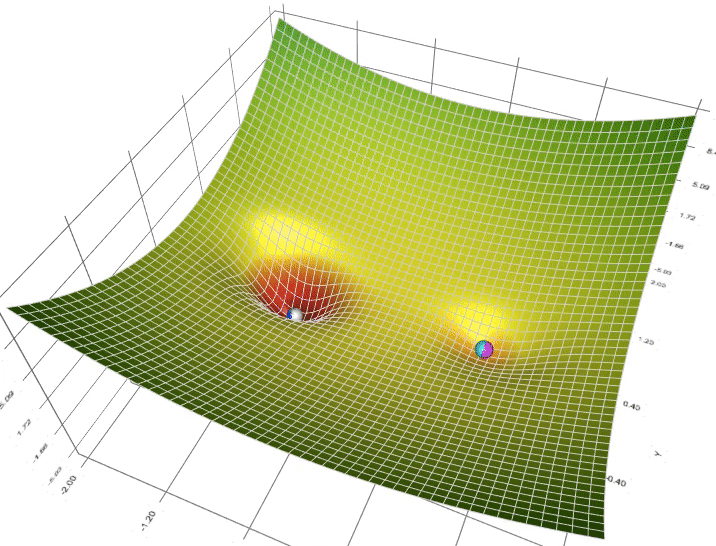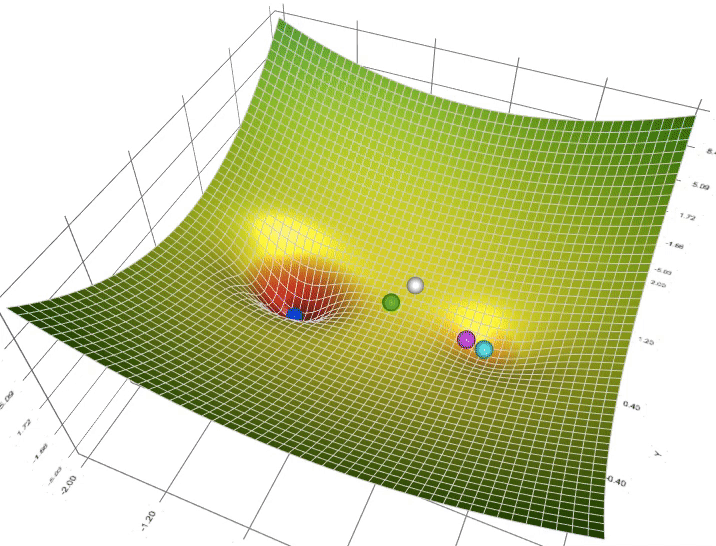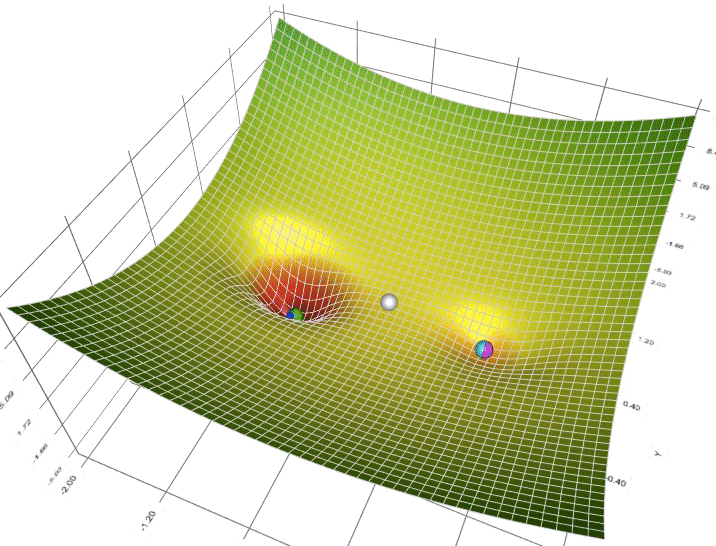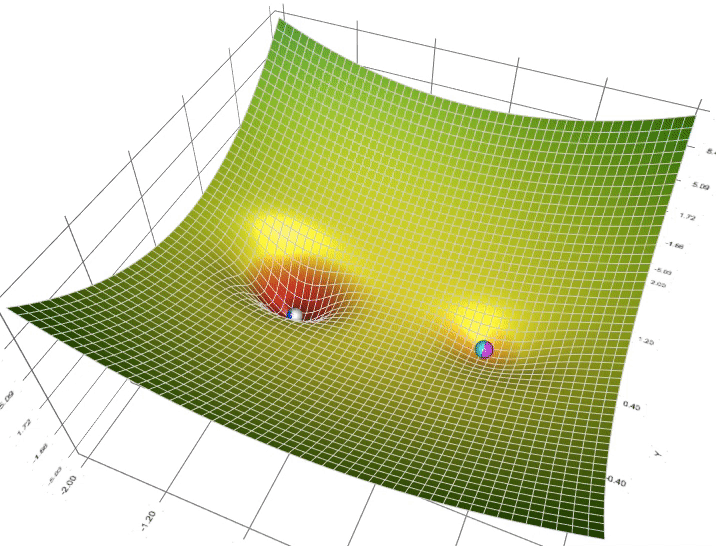
Figure 4: Animation of ADAM (Blue), RMSProp (Green) and AdaGrad(White) compared to SGD (White).

The Adam optimizer is a powerful optimization algorithm that combines the benefits of adaptive learning rates and momentum-based optimization, making it highly effective for training deep neural networks. Unlike standard stochastic gradient descent (SGD), Adam adapts the learning rate for each parameter individually by maintaining running averages of both the first and second moments of the gradients. This adaptive approach allows for efficient convergence even in the presence of noisy gradients or sparse features.

The parameter update rule in Adam is given by:

$$ \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t, $$

where:

• $\theta_t$ is the parameter value at iteration ttt,

• $\eta$ is the learning rate, controlling the step size,

• $\hat{m}_t$ is the bias-corrected estimate of the first moment (mean) of the gradients,

• $\hat{v}_t$ is the bias-corrected estimate of the second moment (uncentered variance) of the gradients,

• $\epsilon$ is a small constant (e.g., $10^{-8}$) added to prevent division by zero.

The first moment estimate, $m_t$, captures the exponentially decayed average of past gradients, introducing momentum to stabilize updates and accelerate convergence in relevant directions. Simultaneously, the second moment estimate, $v_t$, tracks the exponentially decayed average of the squared gradients, allowing the algorithm to scale updates based on the magnitude of the gradients. Both moments are corrected for bias during the early iterations using their respective bias-corrected forms $\hat{m}_t$ and $\hat{v}_t$.

By combining these mechanisms, Adam provides robust and adaptive parameter updates, enabling faster and more stable convergence across a wide range of optimization problems. Its ability to dynamically adjust learning rates for each parameter makes it particularly well-suited for high-dimensional and complex optimization landscapes, such as those encountered in deep learning tasks.

Adam adapts the learning rate for each parameter individually, scaling it inversely proportional to the square root of the estimated variance, which helps in dealing with sparse gradients and noisy loss functions common in RL.

RMSProp is another optimizer designed to handle non-stationary objectives, which are prevalent in RL due to the changing policies and value estimates. RMSProp adjusts the learning rate based on a moving average of squared gradients:

$$ v_t = \beta v_{t-1} + (1 - \beta) g_t^2, $$

$$ \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{v_t} + \epsilon} g_t, $$

where $\beta$ is typically set to 0.9. By dividing the learning rate by the root mean square (RMS) of recent gradients, RMSProp normalizes the parameter updates, preventing them from becoming too large and ensuring more stable convergence.

AdaGrad adapts the learning rate for each parameter based on the accumulated squared gradients from the beginning of training:

$$ G_t = G_{t-1} + g_t^2, $$

$$ \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{G_t} + \epsilon} g_t, $$

where $G_t$ is a diagonal matrix containing the sum of the squares of the gradients with respect to each parameter up to time ttt. AdaGrad is effective for problems with sparse rewards, as it increases the learning rate for infrequently updated parameters, allowing the optimizer to make larger updates when necessary.

Optimization in deep RL presents unique challenges that distinguish it from supervised learning. These challenges stem from the interactive nature of RL, the temporal dependency of data, and the inherent instability in training agents that learn from their own experience.

In RL, the data distribution is non-stationary because the agent's policy, which determines the data it collects, evolves during training. This non-stationarity can lead to unstable gradients, causing oscillations or divergence in the training process. The sequential dependency of states and actions exacerbates this issue, as small changes in the policy can significantly alter future states and rewards.

Many RL environments provide infrequent or delayed rewards, resulting in sparse and noisy gradient estimates. When rewards are sparse, the agent receives less feedback about the effectiveness of its actions, making it difficult to compute reliable gradients for updating the network parameters. This sparsity can slow down learning and requires the optimizer to handle high variance in the gradient estimates.

The temporal credit assignment problem is a core challenge in RL, where the agent must determine which actions are responsible for future rewards. Since rewards may be delayed by many time steps, the optimizer must accurately backpropagate the reward signal through time to adjust the parameters appropriately. This delay complicates the optimization landscape, as the network must capture long-term dependencies.

To address these challenges, various strategies have been developed to stabilize training and improve convergence in deep RL.

Introduced in deep Q-networks (DQNs), target networks help stabilize the training by providing a consistent set of parameters for computing target values in the temporal difference (TD) error. A target network $\theta^-$ is a delayed copy of the primary network $\theta$, updated less frequently:

$$ \theta^- \leftarrow \theta \quad \text{every} \quad N \quad \text{steps}. $$

By keeping the target network fixed for several updates, the method reduces the moving target problem, where both the estimated values and the target values are changing simultaneously, leading to instability.

Gradient clipping is a technique used to prevent exploding gradients, which can occur in recurrent architectures or when dealing with high variability in RL environments. By clipping the gradients to a predefined threshold, the optimizer ensures that parameter updates remain within reasonable bounds:

$$ g_t = \text{clip}(g_t, -k, k), $$

where $k$ is the clipping threshold. This technique helps maintain stable learning dynamics and prevents the optimizer from making drastic updates that could destabilize training.

Experience replay involves storing past experiences in a memory buffer and sampling mini-batches uniformly or according to some priority for training. This approach breaks the correlations between sequential data and smooths out learning by providing a more stationary data distribution. It allows the optimizer to learn from a more diverse set of experiences, improving gradient estimates and convergence.

Applying normalization methods such as batch normalization or layer normalization can help stabilize training by reducing internal covariate shift. Normalization adjusts the inputs to each layer to have zero mean and unit variance, which can improve the optimizer's effectiveness and speed up training.

Implementing optimization algorithms for reinforcement learning (RL) in Rust demands a meticulous approach to balance performance and flexibility. Rust’s focus on zero-cost abstractions, memory safety, and concurrency makes it an ideal choice for high-performance neural network training. By leveraging libraries such as ndarray for n-dimensional array manipulations or tch-rs for PyTorch interoperability, developers can implement advanced optimizers like Adam and RMSProp. These tools enable efficient tensor operations and parallelized computations, ensuring that RL agents learn robustly in computationally intensive environments. Rust’s capabilities provide a foundation for scalable, reliable, and efficient systems tailored for state-of-the-art RL applications.

Rust’s ownership model and type system inherently ensure memory safety without compromising execution speed, a critical requirement in RL where real-time performance is often necessary. Its low-level control over memory and efficient concurrency primitives facilitates the implementation of tensor operations, gradient computations, and parallel training pipelines. Libraries like ndarray and autograd crates support the development of custom neural network components, enabling practitioners to fine-tune optimization algorithms and adapt them to specific RL tasks.

Concurrency, a cornerstone of RL training, benefits greatly from Rust’s zero-cost abstractions and native support for multi-threading and asynchronous programming. For instance, experience replay buffers and data loaders can operate concurrently with the training loop, significantly speeding up the learning process. Rust’s concurrency model ensures thread safety and minimizes overhead, making it ideal for deploying RL agents in real-world, performance-critical scenarios.

Interoperability is another strength of Rust in the RL domain. By leveraging foreign function interfaces (FFI), Rust can integrate seamlessly with existing deep learning frameworks, enabling access to GPU acceleration and advanced libraries. This allows developers to offload computationally expensive tasks, such as forward passes and backpropagation, to external frameworks while retaining Rust’s safety and performance benefits for other system components.

Optimization techniques are pivotal in RL, especially given the unique challenges of non-stationarity and sparse rewards. Gradient-based methods like Adam and RMSProp offer tailored solutions to these issues, improving convergence and stability in environments with dynamic or delayed feedback. Implementing these methods in Rust amplifies their benefits, as the language’s efficiency and safety features allow for the development of highly reliable and performant RL systems. This synergy between advanced optimization techniques and Rust’s robust ecosystem positions developers to tackle the computational and algorithmic complexities of modern RL tasks.

This experiment compares the performance of three popular optimization algorithms—SGD, Adam, and RMSprop—on training a neural network for a binary classification task. The dataset consists of points sampled within concentric circular patterns, and the network's performance is evaluated based on its loss curve and final accuracy. The aim is to understand how different optimizers affect the convergence rate and final model accuracy.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use plotters::prelude::*;
use rand::Rng;
use tch::{nn, Device, Kind, Tensor};
use tch::nn::{ModuleT, OptimizerConfig};

// Custom sequential network 
fn create_network(vs: &nn::VarStore) -> nn::Sequential {
    let root = vs.root();
    nn::seq()
        .add(nn::linear(&root, 2, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&root, 8, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&root, 8, 8, Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(&root, 8, 2, Default::default()))
}

// Function to generate circular dataset
fn generate_dataset(n_samples: usize) -> (Vec<[f64; 2]>, Vec<i64>) {
    let mut rng = rand::thread_rng();
    let mut data = Vec::new();
    let mut labels = Vec::new();

    for _ in 0..n_samples {
        let r = rng.gen_range(0.0..2.0);
        let theta = rng.gen_range(0.0..(2.0 * std::f64::consts::PI));
        let x = r * theta.cos();
        let y = r * theta.sin();
        data.push([x, y]);
        labels.push(if r < 1.0 { 0 } else { 1 });
    }

    (data, labels)
}

// Function to train and evaluate network with different optimizers
fn train_network(
    net: &nn::Sequential,
    data: &Tensor,
    labels: &Tensor,
    vs: &nn::VarStore,
    learning_rate: f64,
    optimizer_name: &str,
) -> (f64, Vec<f64>) {
    let mut loss_history = Vec::new();
    
    // Create optimizer based on name
    let mut opt = match optimizer_name {
        "Sgd" => nn::Sgd::default().build(vs, learning_rate).unwrap(),
        "Adam" => nn::Adam::default().build(vs, learning_rate).unwrap(),
        "RmsProp" => nn::RmsProp::default().build(vs, learning_rate).unwrap(),
        _ => panic!("Unsupported optimizer"),
    };

    for epoch in 1..=1500 {
        // Forward pass
        let preds = net.forward_t(data, true);

        // Compute loss
        let loss = preds.cross_entropy_for_logits(labels);

        // Backward pass and optimization
        opt.zero_grad();
        loss.backward();
        opt.step();

        // Record loss every 10 epochs
        if epoch % 10 == 0 {
            loss_history.push(loss.double_value(&[]));
        }
    }

    // Compute accuracy
    let preds = net.forward_t(data, false).argmax(1, false);
    let accuracy = preds.eq_tensor(labels).to_kind(Kind::Float).mean(Kind::Float);
    
    (accuracy.double_value(&[]) * 100.0, loss_history)
}

// Function to visualize loss curves
fn visualize_loss_curves(
    loss_histories: &[(&str, Vec<f64>)],
    accuracies: &[(&str, f64)],
) -> Result<(), Box<dyn std::error::Error>> {
    let filename = "optimizer_comparison.png";
    let root = BitMapBackend::new(filename, (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .caption("Optimizer Performance Comparison", ("sans-serif", 30))
        .margin(5)
        .x_label_area_size(30)
        .y_label_area_size(30)
        .build_cartesian_2d(0usize..50, 0.0..2.0)?;

    chart.configure_mesh().draw()?;

    // Plot loss curves
    for (i, (name, loss_history)) in loss_histories.iter().enumerate() {
        let color = match i {
            0 => &BLUE,
            1 => &RED,
            2 => &GREEN,
            _ => &BLACK,
        };

        chart.draw_series(
            loss_history.iter().enumerate().map(|(x, &y)| 
                Circle::new((x, y), 2, color.filled())
            )
        )?.label(format!("{} (Acc: {:.2}%)", name, accuracies[i].1))
        .legend(move |(x, y)| 
            Circle::new((x, y), 5, color.filled())
        );
    }

    chart.configure_series_labels()
        .border_style(&BLACK)
        .draw()?;

    root.present()?;
    Ok(())
}


fn main() -> Result<(), Box<dyn std::error::Error>> {
    // Set random seed for reproducibility
    tch::maybe_init_cuda();

    // Generate dataset
    let (data, labels) = generate_dataset(1000);
    let data_tensor: Tensor = Tensor::of_slice2(&data)
        .to_kind(Kind::Float)
        .to_device(Device::Cpu);
    let labels_tensor: Tensor = Tensor::of_slice(&labels)
        .to_kind(Kind::Int64)
        .to_device(Device::Cpu);

    // Optimizers to compare
    let optimizers = ["Sgd", "Adam", "RmsProp"];

    // Store loss histories and accuracies
    let mut loss_histories = Vec::new();
    let mut accuracies = Vec::new();

    // Compare different optimizers
    for name in &optimizers {
        println!("\nTraining with {} optimizer", name);

        // Create VarStore and network
        let vs = nn::VarStore::new(Device::Cpu);
        let net = create_network(&vs);

        // Train network
        let (accuracy, loss_history) = train_network(
            &net, 
            &data_tensor, 
            &labels_tensor, 
            &vs, 
            1e-3, 
            name
        );

        loss_histories.push((name.to_string(), loss_history));
        accuracies.push((name.to_string(), accuracy));

        println!("Accuracy with {}: {:.2}%", name, accuracy);
    }

    // Convert to slices for visualization
    let loss_histories_slice: Vec<_> = loss_histories
        .iter()
        .map(|(name, history)| (name.as_str(), history.clone()))
        .collect();
    
    let accuracies_slice: Vec<_> = accuracies
        .iter()
        .map(|(name, accuracy)| (name.as_str(), *accuracy))
        .collect();

    // Visualize loss curves
    visualize_loss_curves(&loss_histories_slice, &accuracies_slice)?;

    println!("\nOptimizer comparison visualization saved!");

    Ok(())
}

The experiment generates a synthetic dataset where points are labeled as belonging to one of two classes based on their distance from the origin. A multi-layer perceptron with three hidden layers is trained using each optimizer (SGD, Adam, and RMSprop). The training process records the cross-entropy loss at regular intervals, which is then plotted as loss curves for each optimizer. Additionally, the accuracy of the final model is calculated and displayed on the visualization to assess the impact of the optimizer on model performance.

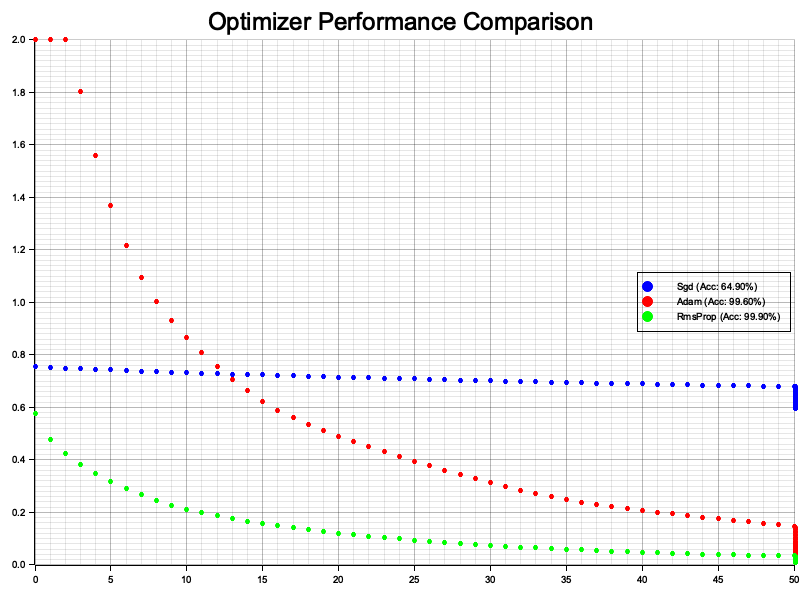
Figure 5: Plotters visualization of optimizer’s performance (SGD, Adam, RMSProp).

The chart visualizes the loss curves for each optimizer. SGD converges slowly and achieves the lowest accuracy (64.90%) due to its fixed learning rate and lack of momentum. Adam, leveraging adaptive learning rates and momentum, converges faster and reaches higher accuracy (98.60%). RMSprop, with its ability to adapt learning rates and smooth gradients for non-convex optimization, achieves the fastest convergence and highest accuracy (99.90%). These results highlight the significance of using adaptive optimizers for complex tasks and noisy gradients.

Optimization techniques are the cornerstone of deep RL, enabling neural networks to learn robust policies and value functions in challenging environments. The integration of advanced algorithms with stability-enhancing strategies like gradient clipping ensures efficient and scalable learning, making them indispensable for modern RL systems.

15.4. Neural Network Architectures link

Neural network architectures form the foundation of deep learning, providing the structural design necessary to process diverse data types and perform complex computational tasks. In reinforcement learning (RL), the architecture of the neural network plays a crucial role in determining the agent's ability to learn, adapt, and generalize. Each architecture is tailored to specific tasks and data characteristics, influencing how policies, value functions, and state representations are modeled. Selecting the right architecture is vital for enabling agents to effectively navigate and make decisions in their environments.

• Feedforward networks, often referred to as fully connected networks, are the most basic architecture. These networks process data in a linear, forward flow from input to output, making them ideal for tasks where the data is already structured or where feature extraction is minimal. Despite their simplicity, they excel in modeling basic policies and value functions in RL. For instance, a feedforward network can be used in environments with well-defined states and actions, where it learns to map inputs directly to outputs.

• Convolutional neural networks (CNNs) extend this capability by introducing spatial awareness, making them indispensable for tasks involving visual data. In RL, CNNs are often employed in environments where agents perceive the world through images, such as video games or robotics. By capturing spatial hierarchies and patterns, CNNs enable agents to extract meaningful features from raw pixel data, such as identifying objects or understanding spatial relationships, enhancing decision-making in visually rich environments.

• Recurrent neural networks (RNNs) and their variants, such as Long Short-Term Memory (LSTM) networks, address scenarios where data has a temporal dimension or where the full state of the environment is not observable at a single timestep. These networks maintain a hidden state that evolves over time, allowing them to encode sequences of observations and infer long-term dependencies. In RL, this ability is critical for partially observable environments, such as tracking moving targets or navigating through uncertain terrains.

• Attention-based models, including Transformers, represent the latest evolution in neural network architectures. These models excel at capturing long-range dependencies and relationships by selectively focusing on relevant parts of the input. In RL, attention mechanisms have proven valuable in tasks requiring complex reasoning or where agents must process multiple inputs simultaneously, such as multi-agent systems or dynamic resource allocation problems.

In practical implementations using Rust, these architectures can be implemented easily with frameworks like tch-rs or ndarray. Rust's emphasis on performance and safety ensures that neural networks can be trained and deployed efficiently, even in resource-constrained environments. Modular design in Rust enables the seamless combination of different architectural components, such as integrating CNNs with RNNs for hybrid tasks. By leveraging these principles and tools, RL practitioners can design robust neural network architectures tailored to the specific needs of their agents, unlocking new levels of performance and adaptability in complex, real-world environments.

Feedforward neural networks are the simplest and most foundational type of neural network, where information flows in one direction—from input to output—through a series of layers without cycles or loops. Each layer applies a linear transformation followed by a non-linear activation function. Mathematically, an FNN is represented as:

$$ f_\theta(\mathbf{x}) = \sigma(\mathbf{W}\mathbf{x} + \mathbf{b}), $$

where $\mathbf{W}$ is the weight matrix, $\mathbf{b}$ is the bias vector, $\sigma$ is an activation function such as ReLU or Sigmoid, and $\theta = \{\mathbf{W}, \mathbf{b}\}$ denotes the network parameters. FNNs are particularly effective in RL tasks where inputs are dense feature vectors, such as in tabular environments or when the state representation is inherently low-dimensional. They are commonly used to approximate value functions or policies in problems where the state and action spaces are manageable in size.

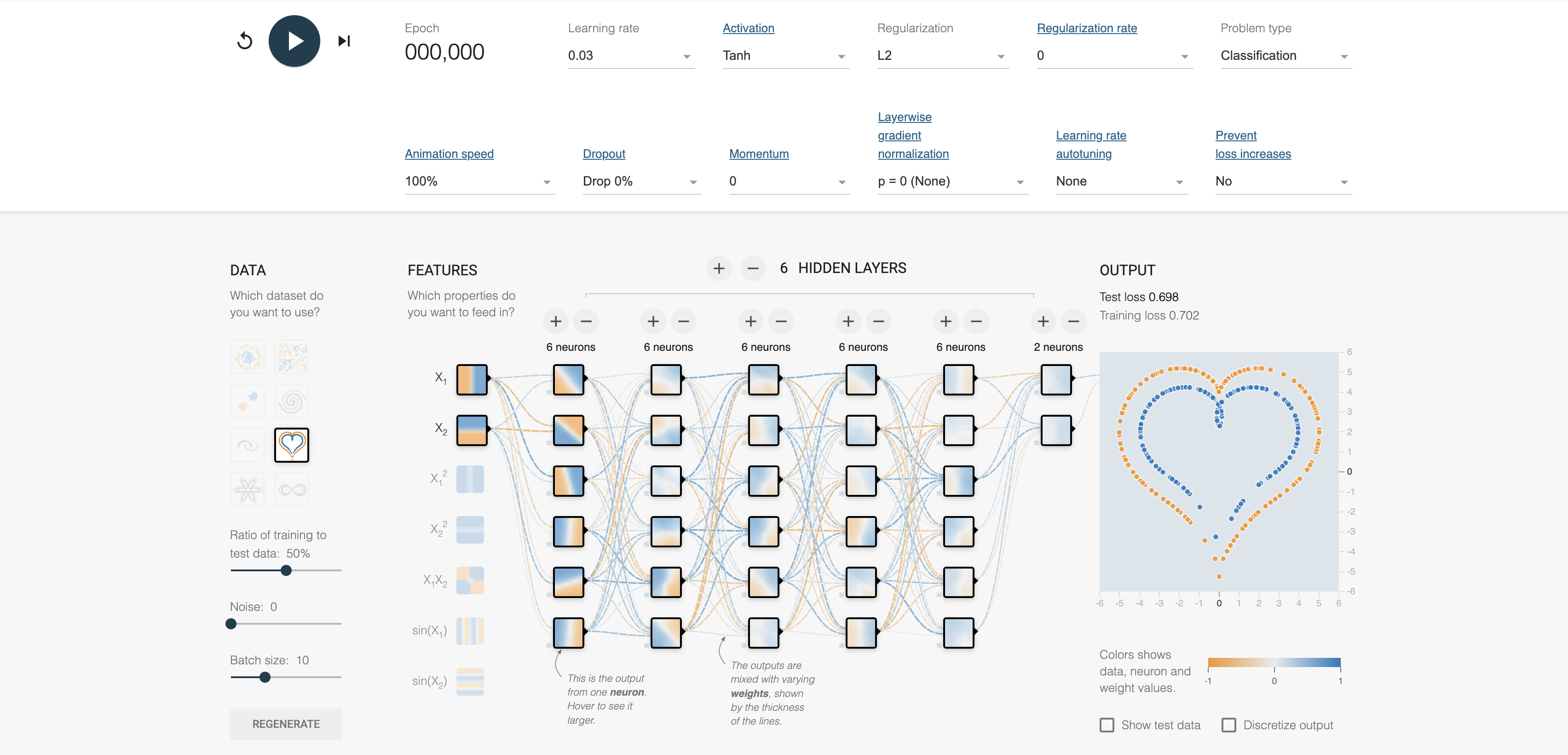
Figure 6: Illustration of FNN from DeeperPlayground tool (Ref:)

A feed-forward neural network processes input data by passing it through multiple layers of interconnected neurons. Each layer applies a weighted transformation followed by a non-linear activation function to capture complex patterns in the data. In the illustration image, the neural network takes two input features ($X_1$ and $X_2$) and processes them through six hidden layers with six neurons each, transforming the data progressively. The lines between neurons represent weights, with thickness indicating their magnitude, and the blue-orange colors depict the activation values. The final layer outputs predictions, here visualized as a classification of points into two classes (blue and orange) forming a heart-shaped boundary. The network's training minimizes loss by adjusting weights iteratively, achieving a balance between training and test performance as shown by the loss values.

Convolutional neural networks (CNNs) are designed to process data with a known grid-like topology, such as images, audio spectrograms, or spatial observations in grid-based environments. CNNs employ convolutional layers that apply filters (kernels) to local regions of the input, capturing spatial hierarchies and local correlations. A convolution operation for a two-dimensional input is defined as:

$$ z_{i,j} = (\mathbf{W} * \mathbf{X})_{i,j} + b = \sum_{k,l} w_{k,l} \, x_{i+k, j+l} + b, $$

where $\mathbf{W}$ is the filter matrix, $\mathbf{X}$ is the input matrix, $w_{k,l}$ are the filter weights, $x_{i+k, j+l}$ is the input value at position $(i+k, j+l)$, and $b$ is the bias term. CNNs are parameter-efficient due to weight sharing and are inherently translationally invariant, making them well-suited for RL tasks involving visual data, such as playing video games or robotic vision applications. In these tasks, the agent must interpret high-dimensional sensory inputs and extract relevant features to inform decision-making.

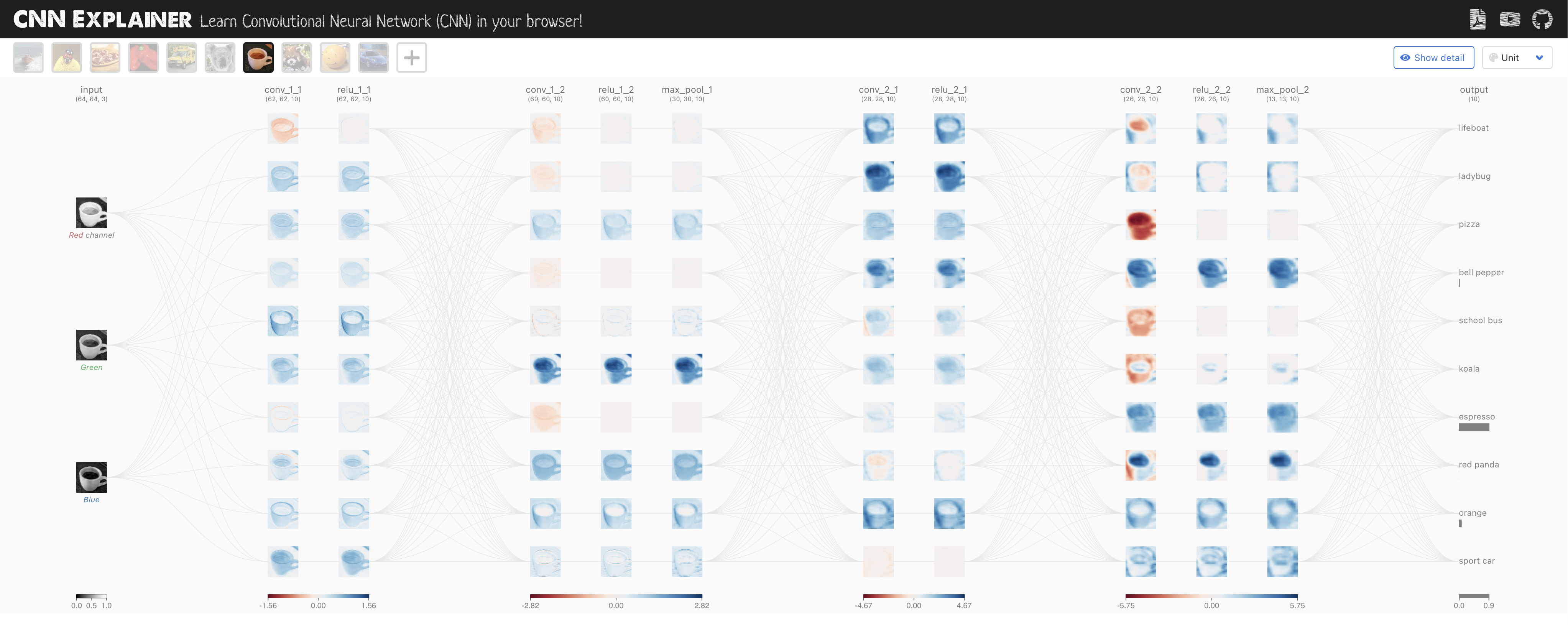
Figure 7: Illustration of convolutional neural networks from CNN Explainer (Ref:https://poloclub.github.io/cnn-explainer)

A Convolutional Neural Network (CNN) processes input data, such as images, by extracting hierarchical patterns through layers of convolutional and pooling operations. The diagram from the CNN Explainer, illustrates how an input image (a coffee cup) is passed through the network's layers. Initially, the image is decomposed into its red, green, and blue channels. Convolutional layers then apply filters to detect edges, textures, and other features, with activations visualized as intensity maps. These features are refined through multiple convolutional and ReLU (activation) layers, and pooling layers reduce spatial dimensions to retain only the most significant information. The network progressively builds a feature hierarchy, with later layers capturing complex patterns, such as the cup's overall shape. Finally, the output layer assigns probabilities to predefined classes (e.g., "espresso" or "orange"), indicating the network's classification decision. This structured feature extraction enables CNNs to recognize intricate visual patterns effectively.

Recurrent neural networks are specialized for processing sequential data, where the current output depends not only on the current input but also on the sequence of previous inputs. RNNs introduce the concept of a hidden state that captures information from prior time steps. The hidden state $\mathbf{h}_t$ at time $t$ is updated using:

$$ \mathbf{h}_t = f(\mathbf{W}_h \mathbf{h}_{t-1} + \mathbf{W}_x \mathbf{x}_t + \mathbf{b}), $$

where $\mathbf{h}_{t-1}$ is the hidden state from the previous time step, $\mathbf{x}_t$ is the current input, $\mathbf{W}_h$ and $\mathbf{W}_x$ are weight matrices for the hidden state and input, respectively, and $f$ is an activation function. However, standard RNNs struggle with learning long-term dependencies due to the vanishing or exploding gradient problem.

Long Short-Term Memory networks address this limitation by incorporating gating mechanisms that regulate the flow of information:

$$ \begin{align*}\mathbf{f}_t &= \sigma(\mathbf{W}_f \mathbf{x}_t + \mathbf{U}_f \mathbf{h}_{t-1} + \mathbf{b}_f), \\ \mathbf{i}_t &= \sigma(\mathbf{W}_i \mathbf{x}_t + \mathbf{U}_i \mathbf{h}_{t-1} + \mathbf{b}_i), \\ \mathbf{o}_t &= \sigma(\mathbf{W}_o \mathbf{x}_t + \mathbf{U}_o \mathbf{h}_{t-1} + \mathbf{b}_o), \\ \mathbf{c}_t &= \mathbf{f}_t \odot \mathbf{c}_{t-1} + \mathbf{i}_t \odot \tanh(\mathbf{W}_c \mathbf{x}_t + \mathbf{U}_c \mathbf{h}_{t-1} + \mathbf{b}_c), \\ \mathbf{h}_t &= \mathbf{o}_t \odot \tanh(\mathbf{c}_t), \end{align*} $$

where $\mathbf{f}_t$, $\mathbf{i}_t$, and $\mathbf{o}_t$ are forget, input, and output gates, respectively; $\mathbf{c}_t$ is the cell state; and $\odot$ denotes element-wise multiplication. LSTMs are capable of capturing long-term dependencies, making them suitable for RL tasks involving partially observable environments, where the agent must remember information over time to make optimal decisions.

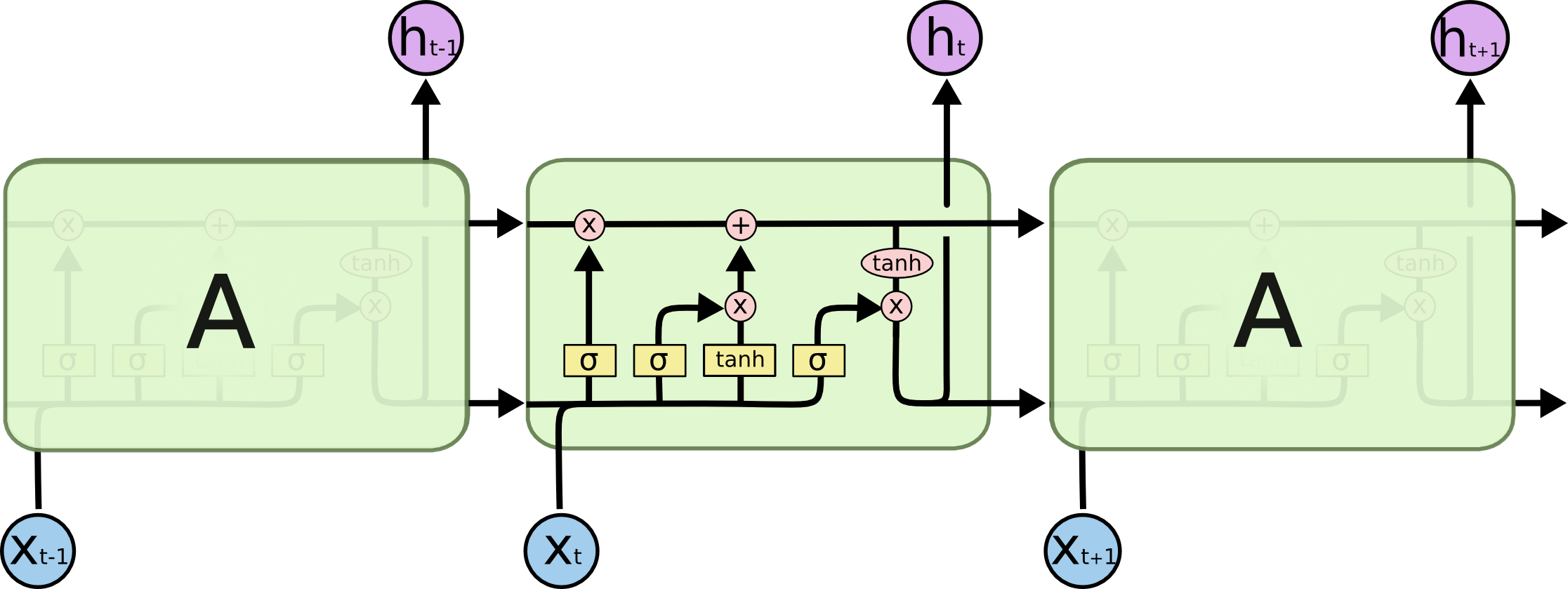
Figure 8: Illustration of LSTM from Colah’s blog (Ref: https://colah.github.io/posts/2015-08-Understanding-LSTMs)

LSTMs are designed to handle sequential data by processing one input at a time while maintaining a hidden state that carries information across time steps. The image illustrates the flow of information in an LSTM. At each time step $t$, the LSTM receives the current input ($X_t$) and combines it with the hidden state from the previous time step ($h_{t-1}$). This combination is passed through activation functions, typically $\tanh$ or $\sigma$ (sigmoid), to compute the updated hidden state ($h_t$). The process repeats for subsequent time steps, allowing the LSTM to model dependencies in the sequence. The loop-like structure of the LSTM enables it to "remember" past information and apply it to current computations, making it ideal for tasks like natural language processing and time series analysis.

Attention mechanisms enhance sequence modeling by allowing models to focus selectively on parts of the input sequence when generating each part of the output sequence. The core idea is to compute a weighted sum of values $\mathbf{V}$, where the weights are determined by the similarity between queries $\mathbf{Q}$ and keys $\mathbf{K}$. The attention function is defined as:

$$ \text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left( \frac{\mathbf{Q} \mathbf{K}^\top}{\sqrt{d_k}} \right) \mathbf{V}, $$

where $d_k$ is the dimensionality of the key vectors, ensuring that the dot products do not become too large. Attention mechanisms enable models to capture dependencies regardless of their distance in the sequence, overcoming the limitations of fixed-size context windows in traditional RNNs.

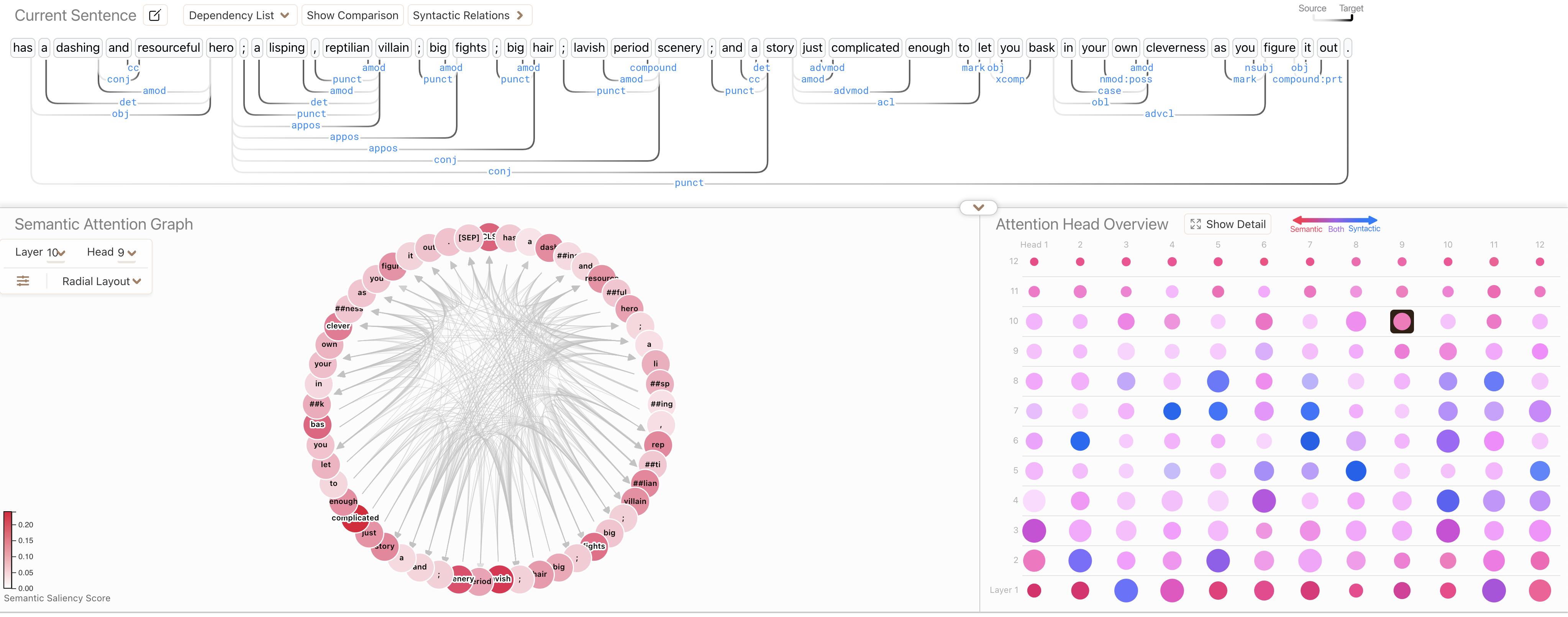
Figure 9: Illustration of attention and multi-head attention from Dodrio (ref: https://poloclub.github.io/dodrio)

Attention and multi-head attention mechanisms, as visualized in the Dodrio interface, are foundational to transformer models like BERT. Attention assigns weights to different parts of the input sequence, allowing the model to focus on the most relevant words or tokens for a given context. For example, in the sentence shown, words like "hero" and "villain" are highlighted as carrying more semantic importance relative to other tokens, influencing downstream tasks like text classification or translation.

Multi-head attention extends this mechanism by enabling the model to focus on multiple aspects of the input simultaneously. Each attention head captures different relationships, such as syntactic (e.g., dependency structure between words) or semantic (e.g., meaning and context of words). In the radial layout, each node represents a token, and the connections depict attention weights learned by a specific head in layer 10. The varying thickness and color intensity of the connections indicate the strength of attention weights, with darker connections showing higher focus. The attention head overview provides a summary of all heads in the model, indicating which heads prioritize semantic (red), syntactic (blue), or both types of information.

This combination of multiple attention heads helps the model capture richer representations of the input, balancing both global (long-term dependencies) and local (context-specific) relationships, enhancing its ability to perform tasks like language understanding and generation effectively.

Transformers are a class of models that rely entirely on attention mechanisms without using recurrence. They process input sequences in parallel, making them highly efficient for large-scale tasks. A Transformer layer combines self-attention with position-wise feedforward networks and layer normalization:

$$ \begin{align*} \mathbf{H}_i &= \text{LayerNorm}\left( \mathbf{X}_i + \text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) \right), \\ \mathbf{O}_i &= \text{LayerNorm}\left( \mathbf{H}_i + \text{FFN}(\mathbf{H}_i) \right), \end{align*} $$

where $\text{FFN}$ is a feedforward network applied to each position separately and identically. Transformers have become the foundation of state-of-the-art architectures in various domains, including RL tasks like language-based navigation, multi-agent coordination, and scenarios where capturing global dependencies is crucial.

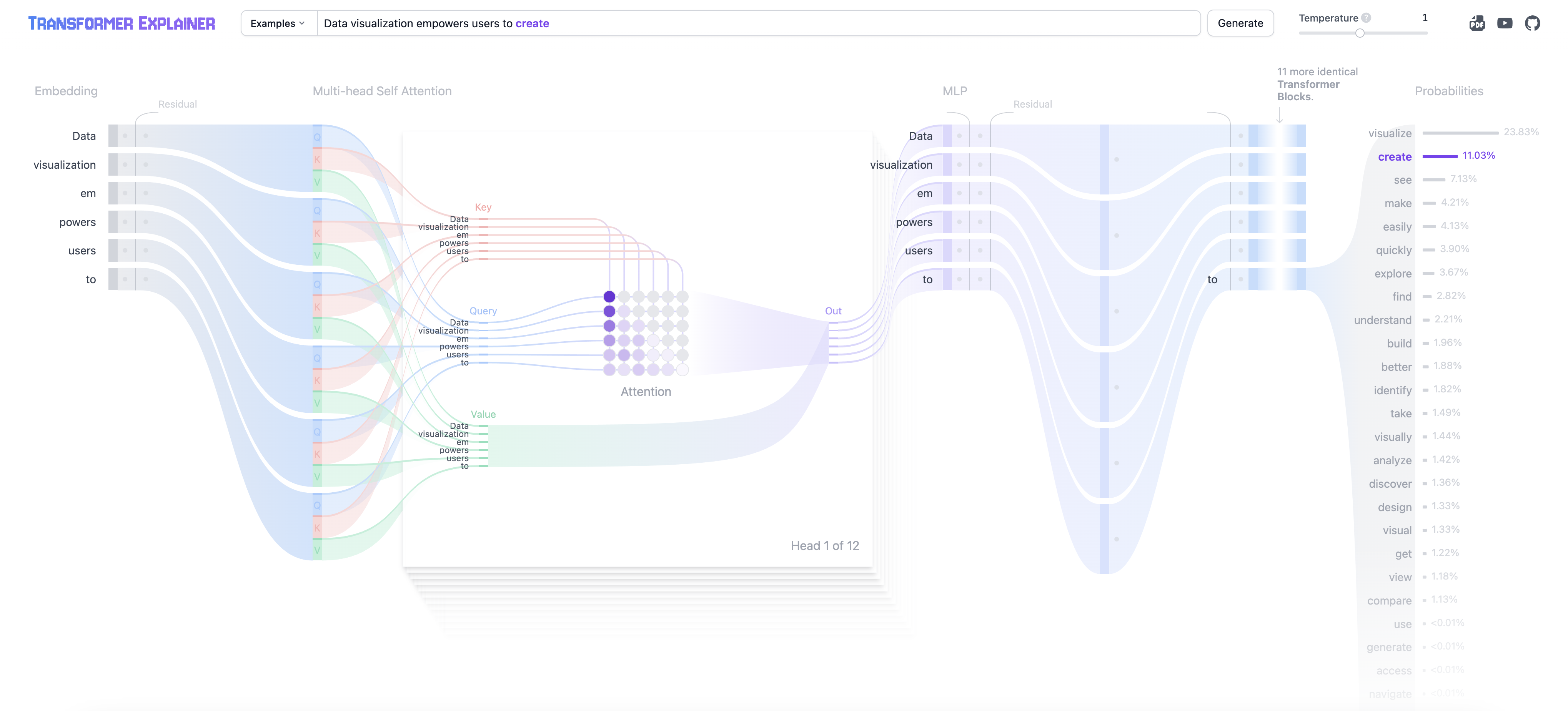
Figure 10: Illustration of Transformer from Transformer Explainer (Ref: https://poloclub.github.io/transformer-explainer)

Transformers, as visualized in the Transformer Explainer, are a type of neural network architecture designed for sequence modeling and understanding relationships in data. The process begins with input tokens (e.g., "Data visualization empowers users to create") being embedded into a continuous vector space. These embeddings pass through multiple transformer blocks that consist of two main components: multi-head self-attention and feed-forward layers (MLPs).

In the multi-head self-attention mechanism, each token generates three vectors: query (Q), key (K), and value (V). Attention scores are computed by comparing the query of one token with the keys of all tokens, determining how much focus each token should give to others. These scores are used to weight the value vectors, producing a weighted representation of the input. Multiple attention heads independently compute these relationships, enabling the model to capture diverse linguistic patterns, such as syntax and semantics.

After attention is computed, the outputs are passed through a residual connection and normalized before being fed into the feed-forward layer, which applies transformations to refine the representation. The process repeats across several transformer blocks, gradually building a rich, context-aware representation of the input sequence.

At the end, the output probabilities (e.g., predicting "create" in this example) are computed by a softmax layer, with attention enabling the model to focus on relevant words across the sequence. This architecture’s ability to consider global context makes transformers highly effective for tasks like language translation, text summarization, and question answering.

Selecting the appropriate neural network architecture in RL depends on the nature of the environment, the state and action spaces, and the specific task at hand.

• Feedforward networks are suitable for RL tasks with low-dimensional, dense feature representations. They are often employed in value function approximation, policy networks in simple environments, and scenarios where the state does not exhibit temporal dependencies.

• Convolutional neural networks are essential in RL tasks involving spatial data, such as visual inputs from environments like Atari games or robotic manipulators. CNNs enable agents to extract hierarchical features from raw pixel data, learning to recognize objects, obstacles, and other relevant spatial patterns.

• Recurrent neural networks and LSTMs are effective in environments where the agent's observations are partial or the state is not fully observable at each time step. They allow the agent to maintain a memory of past observations, capturing temporal dependencies necessary for decision-making in tasks like speech recognition or navigation based on sequential sensory inputs.

• Attention mechanisms and Transformers are increasingly used in RL for tasks that require modeling long-range dependencies or when the environment presents complex interactions between entities. In multi-agent RL, attention allows agents to focus on relevant other agents or environmental factors. Transformers enable scalable training and efficient handling of long sequences, facilitating applications in natural language processing within RL, such as instruction following or dialogue-based tasks.

Rust offers performance and safety advantages for implementing neural network architectures in RL applications. With its strong emphasis on memory safety and concurrency, Rust enables developers to write efficient, parallelizable code without the overhead associated with garbage-collected languages.

Implementing neural networks in Rust involves utilizing libraries and frameworks that support tensor operations and automatic differentiation. Libraries such as tch-rs, which provides Rust bindings for PyTorch, allow for leveraging existing deep learning functionalities while benefiting from Rust's safety features.

By integrating neural network architectures into RL agents using Rust, practitioners can develop high-performance RL systems capable of operating in real-time environments or on resource-constrained devices. Rust's capability to interface with low-level hardware acceleration APIs ensures that computationally intensive tasks, such as training CNNs or Transformers, can be executed efficiently.

Neural network architectures play a pivotal role in the success of reinforcement learning agents. The choice of architecture—be it feedforward networks, convolutional networks, recurrent networks, or attention-based models—must align with the characteristics of the RL task and the nature of the input data. Understanding the mathematical foundations and conceptual strengths of each architecture enables practitioners to design agents that learn effectively from their environments.

By implementing these architectures in Rust, developers can harness the language's performance and safety benefits to create robust, scalable RL applications. As RL continues to tackle increasingly complex problems, the synergy between advanced neural network architectures and efficient implementation languages like Rust will be instrumental in pushing the boundaries of what RL agents can achieve.

The following implementation demonstrates feedforward, convolutional, and recurrent architectures in Rust using the tch crate, with an attention-based network for sequential decision-making. By exploring these architectures, readers gain a comprehensive understanding of the role neural networks play in RL tasks. Each architecture offers unique strengths, from feedforward networks for dense data to Transformers for large-scale tasks, making them indispensable for modern RL systems. Rust’s tch crate enables efficient and scalable implementations, bridging theoretical concepts with practical applications.

The first model in the code below is a Feedforward Neural Network (FNN) designed for reinforcement learning tasks in a simulated environment. The network consists of three fully connected layers with ReLU activation, mapping a given state representation to an appropriate action. The model is trained using the Adam optimizer to minimize the mean squared error (MSE) loss between the predicted and expected actions. It operates in an episodic environment where an agent interacts with the environment to maximize rewards while minimizing loss.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use anyhow::Result;
use rand::Rng;
use tch::{
    nn::{self, Module, OptimizerConfig},
    Device, Kind, Tensor,
};

// Struct for tracking performance metrics
struct PerformanceMetrics {
    total_rewards: Vec<f32>,
    episode_lengths: Vec<usize>,
    cumulative_loss: Vec<f64>,
}

impl PerformanceMetrics {
    fn new() -> Self {
        PerformanceMetrics {
            total_rewards: Vec::new(),
            episode_lengths: Vec::new(),
            cumulative_loss: Vec::new(),
        }
    }

    fn add_episode(&mut self, reward: f32, length: usize, loss: f64) {
        self.total_rewards.push(reward);
        self.episode_lengths.push(length);
        self.cumulative_loss.push(loss);
    }

    fn calculate_stats(&self) -> (f32, f32, f32, f32, f64) {
        let avg_reward = self.total_rewards.iter().sum::<f32>() / self.total_rewards.len() as f32;
        let max_reward = *self.total_rewards.iter().max_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
        let min_reward = *self.total_rewards.iter().min_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
        let avg_episode_length = self.episode_lengths.iter().sum::<usize>() as f32 / self.episode_lengths.len() as f32;
        let avg_loss = self.cumulative_loss.iter().sum::<f64>() / self.cumulative_loss.len() as f64;
        (avg_reward, max_reward, min_reward, avg_episode_length, avg_loss)
    }
}

// Environment simulation
struct RLEnvironment {
    state_dim: usize,
    current_state: Vec<f32>,
}

impl RLEnvironment {
    fn new(state_dim: usize) -> Self {
        let mut rng = rand::thread_rng();
        RLEnvironment {
            state_dim,
            current_state: (0..state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect(),
        }
    }

    fn step(&mut self, action: &[f32]) -> (Vec<f32>, f32, bool) {
        let reward = -action.iter().map(|&a| a.powi(2)).sum::<f32>();
        self.current_state = self.current_state.iter()
            .zip(action.iter().cycle())
            .map(|(&s, &a)| s + a * 0.1)
            .collect();
        let done = self.current_state.iter().any(|&x| x.abs() > 2.0);
        (self.current_state.clone(), reward, done)
    }

    fn reset(&mut self) {
        let mut rng = rand::thread_rng();
        self.current_state = (0..self.state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect();
    }
}

// Feedforward network for policy
struct FeedforwardNetwork {
    vs: nn::VarStore,
    net: nn::Sequential,
}

impl FeedforwardNetwork {
    fn new(state_dim: usize, action_dim: usize) -> Self {
        let vs = nn::VarStore::new(Device::Cpu);
        let net = nn::seq()
            .add(nn::linear(&vs.root(), state_dim as i64, 64, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&vs.root(), 64, 32, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&vs.root(), 32, action_dim as i64, Default::default()));
        FeedforwardNetwork { vs, net }
    }

    fn forward(&self, state: &Tensor) -> Tensor {
        self.net.forward(state)
    }

    fn train(&mut self, states: &Tensor, actions: &Tensor) -> Result<f64> {
        let mut opt = nn::Adam::default().build(&self.vs, 1e-3)?; // Adjust learning rate as needed
        let preds = self.forward(states);

        // Calculate Mean Squared Error Loss
        let loss = preds.mse_loss(actions, tch::Reduction::Mean);

        // Backward pass
        opt.backward_step(&loss);

        Ok(loss.double_value(&[]))
    }
}

// RL Agent
struct RLAgent {
    network: FeedforwardNetwork,
    performance_metrics: PerformanceMetrics,
}

impl RLAgent {
    fn new(state_dim: usize, action_dim: usize) -> Self {
        RLAgent {
            network: FeedforwardNetwork::new(state_dim, action_dim),
            performance_metrics: PerformanceMetrics::new(),
        }
    }

    fn choose_action(&self, state: &Tensor) -> Tensor {
        self.network.forward(state)
    }

    fn train(&mut self, states: &Tensor, actions: &Tensor) -> Result<f64> {
        self.network.train(states, actions)
    }
}

// Main function
fn main() -> Result<()> {
    let state_dim = 16;
    let action_dim = 16;
    let episodes = 200;
    let max_steps = 200;

    let mut env = RLEnvironment::new(state_dim);
    let mut agent = RLAgent::new(state_dim, action_dim);

    for episode in 0..episodes {
        env.reset();
        let mut total_reward = 0.0;
        let mut states = Vec::new();
        let mut actions = Vec::new();

        for _ in 0..max_steps {
            let state_tensor = Tensor::of_slice(&env.current_state)
                .view([1, state_dim as i64])
                .to_kind(Kind::Float);
            let action_tensor = agent.choose_action(&state_tensor);
            let action: Vec<f32> = action_tensor.view([-1]).try_into()?;
            let (_next_state, reward, done) = env.step(&action);

            total_reward += reward;
            states.push(state_tensor);
            actions.push(action_tensor);

            if done {
                break;
            }
        }

        if !states.is_empty() {
            let states_tensor = Tensor::stack(&states, 0);
            let actions_tensor = Tensor::stack(&actions, 0);
            let loss = agent.train(&states_tensor, &actions_tensor)?;
            agent.performance_metrics.add_episode(total_reward, states.len(), loss);
            if episode % 20 == 0 {
                println!("Episode {}: Reward = {:.2}, Loss = {:.6}", episode, total_reward, loss);
            }
        }
    }

    let (avg_reward, max_reward, min_reward, avg_length, avg_loss) = agent.performance_metrics.calculate_stats();
    println!("\nTraining Summary:");
    println!("Average Reward: {:.2}, Max Reward: {:.2}, Min Reward: {:.2}", avg_reward, max_reward, min_reward);
    println!("Average Episode Length: {:.2}, Average Loss: {:.6}", avg_length, avg_loss);

    Ok(())
}

The code integrates the FNN with a reinforcement learning framework that includes an environment, agent, and performance tracking system. The environment simulates a task where the agent performs actions to change its state, receives rewards, and checks for terminal conditions. The FNN acts as a policy network that predicts actions based on the current state. During training, the agent uses gradient descent to refine its policy by minimizing the MSE loss. Metrics such as rewards, episode lengths, and loss are recorded for performance evaluation.

The results from running this code provide key insights into the FNN's performance in reinforcement learning. Over 200 episodes, the network demonstrates its capability to learn an optimal policy, reflected in the progressive improvement in average rewards and reduction in loss. However, as an FNN lacks temporal memory, it may struggle with tasks requiring sequential dependencies, making it suitable for environments where decisions are independent of past states. This limitation highlights the need to compare FNNs with other architectures like CNNs and LSTMs for tasks with complex state representations or temporal relationships.

The second model implemented in this code is a Convolutional Neural Network (CNN) designed to function as a policy network for reinforcement learning. It uses convolutional layers to process state inputs, capturing spatial and structural patterns, which are then passed through a fully connected layer to produce action outputs. The CNN’s architecture includes a 2D convolutional layer followed by max pooling and flattening, enabling the transformation of 2D state representations into actionable insights.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use anyhow::Result;
use rand::Rng;
use tch::{
    nn::{self, Module, OptimizerConfig}, // Import OptimizerConfig here
    Device, Kind, Tensor,
};

// CNN for policy network
struct CNNPolicyNetwork {
    vs: nn::VarStore,
    conv1: nn::Conv2D,
    fc: nn::Linear,
}

impl CNNPolicyNetwork {
    fn new(_state_dim: usize, action_dim: usize) -> Self {
        let vs = nn::VarStore::new(Device::Cpu);

        let conv1 = nn::conv2d(&vs.root(), 1, 16, 3, Default::default());
        let dummy_input = Tensor::zeros(&[1, 1, 4, 4], (Kind::Float, Device::Cpu));
        let output = conv1.forward(&dummy_input).max_pool2d_default(2).flatten(1, -1);
        let flattened_size = output.size()[1] as i64;

        let fc = nn::linear(&vs.root(), flattened_size, action_dim as i64, Default::default());

        CNNPolicyNetwork { vs, conv1, fc }
    }

    fn forward(&self, state: &Tensor) -> Tensor {
        let x = state.view([-1, 1, 4, 4]); // Reshape to 1 channel, 4x4 grid
        let x = self.conv1.forward(&x).relu();
        let x = x.max_pool2d_default(2);
        let x = x.flatten(1, -1); // Flatten for dense layer
        let output = self.fc.forward(&x); // Fully connected layer
        output // Return the output tensor
    }
        

    fn train(&mut self, states: &Tensor, actions: &Tensor) -> Result<f64> {
        // Optimizer setup
        let mut opt = nn::Adam::default().build(&self.vs, 1e-3)?;
        let preds = self.forward(states);
        let loss = preds.mse_loss(actions, tch::Reduction::Mean);
        opt.backward_step(&loss);
        Ok(loss.double_value(&[]))
    }
}
// Struct for tracking performance metrics
struct PerformanceMetrics {
    total_rewards: Vec<f32>,
    episode_lengths: Vec<usize>,
    cumulative_loss: Vec<f64>,
}

impl PerformanceMetrics {
    fn new() -> Self {
        PerformanceMetrics {
            total_rewards: Vec::new(),
            episode_lengths: Vec::new(),
            cumulative_loss: Vec::new(),
        }
    }

    fn add_episode(&mut self, reward: f32, length: usize, loss: f64) {
        self.total_rewards.push(reward);
        self.episode_lengths.push(length);
        self.cumulative_loss.push(loss);
    }

    fn calculate_stats(&self) -> (f32, f32, f32, f32, f64) {
        let avg_reward = self.total_rewards.iter().sum::<f32>() / self.total_rewards.len() as f32;
        let max_reward = *self.total_rewards.iter().max_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
        let min_reward = *self.total_rewards.iter().min_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
        let avg_episode_length = self.episode_lengths.iter().sum::<usize>() as f32 / self.episode_lengths.len() as f32;
        let avg_loss = self.cumulative_loss.iter().sum::<f64>() / self.cumulative_loss.len() as f64;
        (avg_reward, max_reward, min_reward, avg_episode_length, avg_loss)
    }
}

// Environment simulation
struct RLEnvironment {
    _state_dim: usize,
    current_state: Vec<f32>,
}

impl RLEnvironment {
    fn new(state_dim: usize) -> Self {
        let mut rng = rand::thread_rng();
        RLEnvironment {
            _state_dim: state_dim,
            current_state: (0..state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect(),
        }
    }

    fn step(&mut self, action: &[f32]) -> (Vec<f32>, f32, bool) {
        // Ensure action is reshaped if needed
        let reshaped_action: Vec<f32> = action.iter().cloned().collect(); // Example: No reshaping here
    
        // Calculate reward and update state
        let reward = -reshaped_action.iter().map(|&a| a.powi(2)).sum::<f32>();
        self.current_state = self.current_state.iter()
            .zip(reshaped_action.iter().cycle())
            .map(|(&s, &a)| s + a * 0.1)
            .collect();
    
        // Check for termination condition
        let done = self.current_state.iter().any(|&x| x.abs() > 2.0);
        (self.current_state.clone(), reward, done)
    }
    
    fn reset(&mut self) {
        let mut rng = rand::thread_rng();
        self.current_state = (0..self._state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect();
    }
}


// RL Agent
struct RLAgent {
    network: CNNPolicyNetwork,
    performance_metrics: PerformanceMetrics,
}

impl RLAgent {
    fn new(state_dim: usize, action_dim: usize) -> Self {
        RLAgent {
            network: CNNPolicyNetwork::new(state_dim, action_dim),
            performance_metrics: PerformanceMetrics::new(),
        }
    }

    fn choose_action(&self, state: &Tensor) -> Tensor {
        let raw_action = self.network.forward(state); // CNN output
        // Reshape or process action if necessary
        let processed_action = raw_action.view([-1, 16]); // Ensure compatibility with environment
        processed_action
    }
    

    fn train(&mut self, states: &Tensor, actions: &Tensor) -> Result<f64> {
        self.network.train(states, actions)
    }
}

// Main function
fn main() -> Result<()> {
    let state_dim = 16;
    let action_dim = 16;
    let episodes = 200;
    let max_steps = 200;

    let mut env = RLEnvironment::new(state_dim);
    let mut agent = RLAgent::new(state_dim, action_dim);

    for episode in 0..episodes {
        env.reset();
        let mut total_reward = 0.0;
        let mut states = Vec::new();
        let mut actions = Vec::new();

        for _ in 0..max_steps {
            let state_tensor = Tensor::of_slice(&env.current_state)
                .view([1, state_dim as i64])
                .to_kind(Kind::Float);
            let action_tensor = agent.choose_action(&state_tensor);
            let action: Vec<f32> = action_tensor.view([-1]).try_into()?;
            let (_next_state, reward, done) = env.step(&action);

            total_reward += reward;
            states.push(state_tensor);
            actions.push(action_tensor);

            if done {
                break;
            }
        }

        if !states.is_empty() {
            let states_tensor = Tensor::stack(&states, 0); // Stack states along batch dimension
            let actions_tensor = Tensor::stack(&actions, 0).view([-1, 16]); // Match network output shape
        
            let loss = agent.train(&states_tensor, &actions_tensor)?;
            agent.performance_metrics.add_episode(total_reward, states.len(), loss);
        
            if episode % 20 == 0 {
                println!("Episode {}: Reward = {:.2}, Loss = {:.6}", episode, total_reward, loss);
            }
        }
        
    }

    let (avg_reward, max_reward, min_reward, avg_length, avg_loss) = agent.performance_metrics.calculate_stats();
    println!("\nTraining Summary:");
    println!("Average Reward: {:.2}, Max Reward: {:.2}, Min Reward: {:.2}", avg_reward, max_reward, min_reward);
    println!("Average Episode Length: {:.2}, Average Loss: {:.6}", avg_length, avg_loss);

    Ok(())
}

The CNN model is embedded within an RL framework where an agent interacts with a simulated environment. The environment provides state inputs and rewards based on the agent's actions. The CNN processes state inputs reshaped into 4x4 grids, extracts features through convolution, and maps them to actions. The agent learns by minimizing the mean squared error (MSE) loss between predicted and expected actions using the Adam optimizer. Performance metrics such as rewards, episode lengths, and cumulative loss are tracked across episodes to evaluate learning progress.

The results from the model's training demonstrate the CNN's ability to effectively capture spatial relationships in the state representation and translate them into optimal actions. As training progresses, average rewards tend to increase, and loss decreases, showcasing improved policy performance. Compared to simpler models like feedforward networks, CNNs can handle more complex, structured inputs, making them suitable for tasks with spatial dependencies. However, for temporal dependencies, alternative architectures like LSTMs might outperform CNNs, underlining the importance of selecting the right architecture for the task.

The next code implements a Long Short-Term Memory (LSTM)-based policy network for reinforcement learning. The LSTM is adept at capturing temporal dependencies in sequential data, making it suitable for environments where actions depend on past states. The architecture includes an LSTM layer with a hidden size of 64 to process sequential inputs, followed by a fully connected layer that maps the LSTM outputs to action predictions. This setup enables the model to learn and predict actions based on both current and past state information.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use anyhow::Result;
use rand::Rng;
use tch::{
    nn::{self, OptimizerConfig, RNN},
    Device, Kind, Tensor,
};

// LSTM for policy network
struct LSTMPolicyNetwork {
    vs: nn::VarStore,
    lstm: nn::LSTM,
    fc: nn::Linear,
}

impl LSTMPolicyNetwork {
    fn new(state_dim: usize, action_dim: usize) -> Self {
        let vs = nn::VarStore::new(Device::Cpu);

        // Define the LSTM layer
        let lstm = nn::lstm(
            &vs.root(),
            state_dim as i64, // Input size
            64,               // Hidden size
            Default::default(),
        );

        // Fully connected layer to map LSTM outputs to action space
        let fc = nn::linear(&vs.root(), 64, action_dim as i64, Default::default());

        LSTMPolicyNetwork { vs, lstm, fc }
    }

    fn forward(&self, state: &Tensor) -> Tensor {
        // Ensure input is 3D with shape [seq_len, batch_size, input_size]
        let x = if state.dim() == 2 {
            state.unsqueeze(0) // If 2D, add seq_len dimension
        } else {
            state.shallow_clone() // Already 3D
        };
            // LSTM forward pass
        let (output, _) = self.lstm.seq(&x);
    
        // Fully connected layer applied to all time steps
        let fc_output = output.apply(&self.fc);
        fc_output
    }
    

    fn train(&mut self, states: &Tensor, actions: &Tensor) -> Result<f64> {
        let mut opt = nn::Adam::default().build(&self.vs, 1e-3)?;
    
        // Predictions from forward pass
        let preds = self.forward(states);
    
        // Align dimensions for loss computation
        let aligned_preds = preds.unsqueeze(2); // Add the missing dimension in preds
    
        // Compute loss
        let loss = aligned_preds.mse_loss(actions, tch::Reduction::Mean);
        opt.backward_step(&loss);
        Ok(loss.double_value(&[]))
    }    
}
// RL Agent
struct RLAgent {
    network: LSTMPolicyNetwork,
    performance_metrics: PerformanceMetrics,
}

impl RLAgent {
    fn new(state_dim: usize, action_dim: usize) -> Self {
        RLAgent {
            network: LSTMPolicyNetwork::new(state_dim, action_dim),
            performance_metrics: PerformanceMetrics::new(),
        }
    }

    fn choose_action(&self, state: &Tensor) -> Tensor {
        self.network.forward(state)
    }

    fn train(&mut self, states: &Tensor, actions: &Tensor) -> Result<f64> {
        self.network.train(states, actions)
    }
}

// Struct for tracking performance metrics
struct PerformanceMetrics {
    total_rewards: Vec<f32>,
    episode_lengths: Vec<usize>,
    cumulative_loss: Vec<f64>,
}

impl PerformanceMetrics {
    fn new() -> Self {
        PerformanceMetrics {
            total_rewards: Vec::new(),
            episode_lengths: Vec::new(),
            cumulative_loss: Vec::new(),
        }
    }

    fn add_episode(&mut self, reward: f32, length: usize, loss: f64) {
        self.total_rewards.push(reward);
        self.episode_lengths.push(length);
        self.cumulative_loss.push(loss);
    }

    fn calculate_stats(&self) -> (f32, f32, f32, f32, f64) {
        let avg_reward = self.total_rewards.iter().sum::<f32>() / self.total_rewards.len() as f32;
        let max_reward = *self.total_rewards.iter().max_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
        let min_reward = *self.total_rewards.iter().min_by(|a, b| a.partial_cmp(b).unwrap()).unwrap();
        let avg_episode_length = self.episode_lengths.iter().sum::<usize>() as f32 / self.episode_lengths.len() as f32;
        let avg_loss = self.cumulative_loss.iter().sum::<f64>() / self.cumulative_loss.len() as f64;
        (avg_reward, max_reward, min_reward, avg_episode_length, avg_loss)
    }
}

// Environment simulation
struct RLEnvironment {
    _state_dim: usize,
    current_state: Vec<f32>,
}

impl RLEnvironment {
    fn new(state_dim: usize) -> Self {
        let mut rng = rand::thread_rng();
        RLEnvironment {
            _state_dim: state_dim,
            current_state: (0..state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect(),
        }
    }

    fn step(&mut self, action: &[f32]) -> (Vec<f32>, f32, bool) {
        let reward = -action.iter().map(|&a| a.powi(2)).sum::<f32>();
        self.current_state = self.current_state.iter()
            .zip(action.iter().cycle())
            .map(|(&s, &a)| s + a * 0.1)
            .collect();
        let done = self.current_state.iter().any(|&x| x.abs() > 2.0);
        (self.current_state.clone(), reward, done)
    }

    fn reset(&mut self) {
        let mut rng = rand::thread_rng();
        self.current_state = (0..self._state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect();
    }
}

// Modify the main function to create tensors with correct shapes
fn main() -> Result<()> {
    let state_dim = 16;
    let action_dim = 16;
    let episodes = 200;
    let max_steps = 200;

    let mut env = RLEnvironment::new(state_dim);
    let mut agent = RLAgent::new(state_dim, action_dim);

    for episode in 0..episodes {
        env.reset();
        let mut total_reward = 0.0;
        let mut states_vec = Vec::new();
        let mut actions_vec = Vec::new();

        for _ in 0..max_steps {
            let state_tensor = Tensor::of_slice(&env.current_state)
                .to_kind(Kind::Float)
                .view([1, state_dim as i64]); // Ensure 2D tensor
            
            let action_tensor = agent.choose_action(&state_tensor);
            let action: Vec<f32> = action_tensor.view([-1]).try_into()?;
            let (_next_state, reward, done) = env.step(&action);

            total_reward += reward;
            states_vec.push(state_tensor);
            actions_vec.push(action_tensor);

            if done {
                break;
            }
        }

        if !states_vec.is_empty() {
            // Stack tensors along the first dimension
            let states_tensor = Tensor::stack(&states_vec, 0); // Shape: [batch_size, seq_len, state_dim]
            let actions_tensor = Tensor::stack(&actions_vec, 0); // Shape: [batch_size, action_dim]

            let loss = agent.train(&states_tensor, &actions_tensor)?;
            agent.performance_metrics.add_episode(total_reward, states_vec.len(), loss);

            if episode % 20 == 0 {
                println!("Episode {}: Reward = {:.2}, Loss = {:.6}", episode, total_reward, loss);
            }
        }
    }

    let (avg_reward, max_reward, min_reward, avg_length, avg_loss) = agent.performance_metrics.calculate_stats();
    println!("\nTraining Summary:");
    println!("Average Reward: {:.2}, Max Reward: {:.2}, Min Reward: {:.2}", avg_reward, max_reward, min_reward);
    println!("Average Episode Length: {:.2}, Average Loss: {:.6}", avg_length, avg_loss);

    Ok(())
}

The reinforcement learning framework pairs the LSTM policy network with an environment simulation. The agent receives state inputs from the environment, processes them through the LSTM network, and generates actions. Rewards are calculated based on the quality of the actions, with the agent learning to minimize the discrepancy between predicted and expected actions using the Adam optimizer and Mean Squared Error (MSE) loss. Performance metrics such as cumulative reward, episode lengths, and training loss are tracked to evaluate the learning process. The model is trained over multiple episodes, with each episode consisting of several interaction steps between the agent and the environment.

The LSTM model excels in tasks with temporal dependencies, as evidenced by its ability to improve rewards over episodes by leveraging sequential state information. Compared to static models like Feedforward Neural Networks, the LSTM shows better adaptability in dynamic environments. As training progresses, the model typically achieves lower loss and higher rewards, indicating successful policy improvement. However, the results may vary depending on the environment's complexity and reward design, underscoring the importance of hyperparameter tuning and sufficient training iterations. The LSTM's performance can also be influenced by the quality of input sequences and the stability of the optimizer.

In summary, the three practical code samples implement distinct neural network architectures—Feedforward Neural Network (FNN), Convolutional Neural Network (CNN), and Recurrent Neural Network (RNN) using LSTM—for reinforcement learning. The FNN uses fully connected layers to process state inputs directly, making it suitable for static environments without temporal or spatial structure. The CNN leverages convolutional layers to extract spatial features, particularly useful for grid-like or image-based state representations, followed by a fully connected layer for action predictions. The RNN (LSTM) processes sequential state inputs to capture temporal dependencies, making it ideal for dynamic environments where actions depend on past states. While the FNN offers simplicity and efficiency for non-sequential data, the CNN adds robustness for spatially structured inputs, and the LSTM excels in scenarios requiring sequential decision-making by leveraging memory across time steps. Each architecture demonstrates strengths tailored to specific reinforcement learning contexts, with their performance varying based on the environment's characteristics and complexity.

15.5. Regularization and Generalization link

Regularization is a foundational concept in deep learning, designed to improve a model's generalization capabilities by mitigating the risk of overfitting. Overfitting occurs when a neural network learns patterns specific to its training data but struggles to adapt to new or unseen scenarios. This issue becomes particularly challenging in reinforcement learning (RL), where agents learn directly from interactions with their environments, which are often dynamic, stochastic, and non-deterministic. In such contexts, regularization helps ensure that the policies and value functions learned by an agent are robust and adaptable, enabling better performance in a variety of real-world or slightly altered conditions.

One of the most common regularization techniques is L2 regularization, also known as weight decay. This approach penalizes large weights in the neural network, encouraging the model to favor simpler and more stable solutions. By constraining the magnitude of the weights, L2 regularization reduces the model's reliance on specific features in the training data, promoting better generalization to unseen environments. In RL, where agents must make decisions based on sparse and noisy feedback, this technique helps stabilize learning and prevents the agent from overfitting to transient patterns in the training data.

Dropout is another powerful regularization method widely used in deep learning, including RL. Dropout works by randomly "dropping out" or deactivating a subset of neurons during training, effectively creating an ensemble of smaller networks. This randomness forces the network to develop more distributed and redundant representations, making it less likely to overfit to specific data points. In RL, where agents often deal with highly variable environments, dropout enhances their ability to adapt by preventing over-reliance on any single pathway in the network.

Batch normalization, though primarily introduced to accelerate training, also plays a significant role in regularization. By normalizing the inputs to each layer, batch normalization reduces internal covariate shifts, making the training process more stable and robust. This technique is particularly beneficial in RL, where the data distribution can change over time as the agent explores different states. By maintaining a consistent scale and distribution of activations, batch normalization ensures that the network remains flexible and effective across diverse scenarios.

The primary objective of any learning algorithm is to minimize the total error, which is composed of three distinct components:

$$ \text{Total Error} = \text{Bias}^2 + \text{Variance} + \text{Irreducible Error}. $$

Bias measures the error introduced by approximating a real-world problem, which may be complex, by a much simpler model.

Variance quantifies the amount by which the model's predictions would change if we used a different training dataset. High variance indicates sensitivity to fluctuations in the training data.

Irreducible Error represents the noise inherent in the system that cannot be eliminated by any model.

Regularization techniques aim to balance the bias-variance trade-off, ensuring that the model is neither too simple (high bias) nor too complex (high variance). By controlling the complexity of the model, regularization enhances its ability to generalize to unseen data, which is especially critical in RL where the agent must perform well in diverse and evolving environments.

L2 regularization, also known as weight decay, penalizes large weights in the neural network by adding the squared magnitude of all weights to the loss function. The modified loss function becomes:

$$ L(\theta) = L_{\text{data}} + \lambda \|\theta\|^2, $$

where:

• $L_{\text{data}}$ is the original loss function (e.g., mean squared error).

• $|\theta\|^2 = \sum_{i} \theta_i^2$ is the squared L2 norm of the weight vector $\theta$.

• $\lambda > 0$ is the regularization parameter controlling the strength of the penalty.

By discouraging excessively large weights, L2 regularization effectively reduces model complexity. In the context of RL, this can prevent the policy or value function approximators from becoming overly sensitive to specific features of the training environment, thus promoting better generalization to new states or unseen environments.

Dropout is a regularization technique that mitigates overfitting by randomly zeroing out a fraction of the neurons' activations during training. For a given layer, each neuron's output is set to zero with a probability $p$, independently of other neurons. Mathematically, the dropout activation $a_i^{\text{dropout}}$ for neuron $i$ is:

$$ a_i^{\text{dropout}} = \begin{cases} a_i, & \text{with probability } 1 - p, \\ 0, & \text{with probability } p, \end{cases} $$

where $a_i$ is the original activation. During inference, to maintain consistency in the expected output, the activations are scaled by a factor of $1 - p$:

$$ a_i^{\text{inference}} = (1 - p) a_i. $$

Dropout prevents neurons from co-adapting to specific features, forcing the network to learn redundant representations. This redundancy enhances the robustness of the model, which is particularly beneficial in RL where the agent must remain resilient to the variability of the environment.

Batch normalization (BN) is a technique to stabilize and normalize the distribution of inputs to each layer during training, thereby addressing the internal covariate shift—the phenomenon where the distribution of layer inputs changes due to updates in preceding layers. Mathematically, for a batch of input features $\{x_i\}_{i=1}^N$, BN transforms each feature $x_i$ as:

$$ \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}, $$

where:

• $\mu_B = \frac{1}{N} \sum_{i=1}^N x_i$ is the mean of the batch,

• $\sigma_B^2 = \frac{1}{N} \sum_{i=1}^N (x_i - \mu_B)^2$ is the variance of the batch,

• $\epsilon$ is a small constant to prevent division by zero.

The normalized inputs $\hat{x}_i$ are further scaled and shifted using learnable parameters $\gamma$ (scale) and $\beta$ (shift):

$$ y_i = \gamma \hat{x}_i + \beta. $$

This transformation ensures that the outputs of a layer remain well-scaled and centered, improving gradient flow and enabling faster convergence. In RL, this stabilization can be particularly beneficial due to the high variance in gradient estimates caused by stochastic policy updates. Batch normalization also stabilizes the learning process by reducing the sensitivity to the initial weights and learning rates, enabling the use of higher learning rates and faster convergence.

In reinforcement learning, agents learn optimal policies through interactions with the environment, which often involves exploration of vast state and action spaces. The challenges of sparse rewards, non-stationarity, and dynamic environments amplify the risk of overfitting. An agent that overfits may learn to exploit specific patterns or anomalies in the training environment that do not generalize to other scenarios, leading to poor performance when conditions change.

Increasing the complexity of the neural network model enhances its capacity to represent intricate policies and value functions. However, this increased capacity can lead to overfitting, where the agent's policy becomes finely tuned to the training environment at the expense of generalization. Regularization techniques help manage this trade-off by constraining the model's complexity, thereby promoting policies that perform well across a broader range of environments.

Entropy regularization is a technique specific to policy-based RL methods, where the objective is to learn a stochastic policy $\pi(a|s)$ that maps states $s$ to a probability distribution over actions aaa. Entropy $H(\pi)$ of the policy is defined as:

$$ H(\pi) = - \sum_{a} \pi(a|s) \log \pi(a|s). $$

Higher entropy corresponds to more randomness in the action selection, encouraging exploration. By adding an entropy term to the loss function, the updated objective becomes:

$$ L = L_{\text{policy}} - \beta H(\pi), $$

where $L_{\text{policy}}$ is the original policy loss (e.g., negative expected return), and$\beta > 0$ is a weighting factor controlling the influence of the entropy term. Entropy regularization penalizes deterministic policies, promoting exploration and preventing the agent from prematurely converging to suboptimal actions. This is crucial in RL, where the agent must balance exploration of new actions with exploitation of known rewarding actions to avoid local optima.

Implementing regularization in Rust for RL applications requires leveraging the language's strengths in performance and modularity. Frameworks such as tch-rs provide the tools to integrate regularization techniques seamlessly into neural network training pipelines. For instance, L2 regularization can be added by modifying the optimizer to include weight decay, while dropout and batch normalization can be implemented as layers within the network architecture. Rust's emphasis on memory safety and concurrency ensures that these implementations are both efficient and reliable, even in computationally demanding RL scenarios. By combining advanced regularization techniques with Rust's capabilities, RL practitioners can build agents that generalize effectively, adapt to diverse environments, and achieve robust performance in complex real-world tasks.

In Rust, adding L2 regularization to the loss function requires computing the squared L2 norm of the model's parameters and incorporating it into the optimization objective. Utilizing libraries that support automatic differentiation, such as autograd, simplifies this process by allowing gradients of the regularization term to be computed alongside the primary loss.

Implementing dropout in Rust involves randomly zeroing out activations during the forward pass. This can be achieved by generating random masks using Rust's random number generation capabilities and applying them to the activation tensors. Care must be taken to ensure that the dropout behavior is only applied during training and not during inference, which can be controlled using Rust's conditional compilation features or runtime flags.

Batch normalization can be implemented by calculating the mean and variance of the activations within each mini-batch and normalizing accordingly. Rust's efficient handling of numerical computations and support for parallelism can accelerate these calculations. Additionally, integrating batch normalization layers into the neural network architecture requires updating the forward and backward passes to include the normalization steps and parameter updates for $\gamma$ and $\beta$.

Regularization is essential for developing reinforcement learning agents that generalize well to new and varied environments. By understanding and applying regularization techniques such as L2 regularization, dropout, batch normalization, and entropy regularization, practitioners can mitigate overfitting and enhance the robustness of their agents. These methods help balance the complexity of the model with its ability to generalize, which is critical in RL tasks characterized by dynamic and uncertain environments.

Implementing these techniques in Rust offers the advantages of high performance and memory safety, enabling the development of efficient and reliable RL systems. Rust's features facilitate the creation of sophisticated models while minimizing the risk of errors, which is especially important in the complex and iterative process of training RL agents.

As reinforcement learning continues to advance and tackle more complex problems, the role of regularization in ensuring the adaptability and resilience of agents will remain a focal point. By integrating robust regularization strategies and leveraging powerful programming languages like Rust, practitioners can push the boundaries of what RL agents can achieve, fostering the development of intelligent systems capable of performing effectively in the real world.

The experiment below aims to evaluate the impact of various regularization methods, including no regularization, L2 regularization, and dropout, on the performance of a feedforward neural network in a reinforcement learning environment. The neural network serves as a policy model, predicting actions based on environmental states. The goal is to assess how these regularization techniques influence training stability, convergence, and rewards over 1000 episodes.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use anyhow::Result;
use plotters::prelude::*;
use rand::Rng;
use tch::{
    nn::{self, Module, OptimizerConfig},
    Device, Kind, Tensor,
};

// Struct for tracking performance metrics
struct PerformanceMetrics {
    total_rewards: Vec<f32>,
    episode_lengths: Vec<usize>,
    cumulative_loss: Vec<f64>,
}

impl PerformanceMetrics {
    fn new() -> Self {
        PerformanceMetrics {
            total_rewards: Vec::new(),
            episode_lengths: Vec::new(),
            cumulative_loss: Vec::new(),
        }
    }

    fn add_episode(&mut self, reward: f32, length: usize, loss: f64) {
        self.total_rewards.push(reward);
        self.episode_lengths.push(length);
        self.cumulative_loss.push(loss);
    }
}

// Environment simulation
struct RLEnvironment {
    state_dim: usize,
    current_state: Vec<f32>,
}

impl RLEnvironment {
    fn new(state_dim: usize) -> Self {
        let mut rng = rand::thread_rng();
        RLEnvironment {
            state_dim,
            current_state: (0..state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect(),
        }
    }

    fn step(&mut self, action: &[f32]) -> (Vec<f32>, f32, bool) {
        let reward = -action.iter().map(|&a| a.powi(2)).sum::<f32>();
        self.current_state = self
            .current_state
            .iter()
            .zip(action.iter().cycle())
            .map(|(&s, &a)| s + a * 0.1)
            .collect();
        let done = self.current_state.iter().any(|&x| x.abs() > 2.0);
        (self.current_state.clone(), reward, done)
    }

    fn reset(&mut self) {
        let mut rng = rand::thread_rng();
        self.current_state = (0..self.state_dim).map(|_| rng.gen_range(-1.0..1.0)).collect();
    }
}

// Regularized Feedforward Network
struct FeedforwardNetwork {
    vs: nn::VarStore,
    layers: nn::Sequential,
    dropout_rate: f64,
}

impl FeedforwardNetwork {
    fn new(state_dim: usize, action_dim: usize, dropout: f64) -> Self {
        let vs = nn::VarStore::new(Device::Cpu);
        let layers = nn::seq()
            .add(nn::linear(&vs.root(), state_dim as i64, 64, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&vs.root(), 64, 32, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&vs.root(), 32, action_dim as i64, Default::default()));
        FeedforwardNetwork {
            vs,
            layers,
            dropout_rate: dropout,
        }
    }

    fn forward(&self, state: &Tensor) -> Tensor {
        let x = self.layers.forward(state);
        x.dropout(self.dropout_rate, true) // Apply dropout
    }

    fn train(
        &mut self,
        states: &Tensor,
        actions: &Tensor,
        weight_decay: f64,
    ) -> Result<f64> {
        let mut opt = nn::Adam {
            wd: weight_decay,
            ..Default::default()
        }
        .build(&self.vs, 1e-3)?;
        let preds = self.forward(states);
        let loss = preds.mse_loss(actions, tch::Reduction::Mean);
        opt.backward_step(&loss);

        Ok(loss.double_value(&[]))
    }
}

// RL Agent
struct RLAgent {
    network: FeedforwardNetwork,
    performance_metrics: PerformanceMetrics,
}

impl RLAgent {
    fn new(state_dim: usize, action_dim: usize, dropout: f64) -> Self {
        RLAgent {
            network: FeedforwardNetwork::new(state_dim, action_dim, dropout),
            performance_metrics: PerformanceMetrics::new(),
        }
    }

    fn choose_action(&self, state: &Tensor) -> Tensor {
        self.network.forward(state)
    }

    fn train(&mut self, states: &Tensor, actions: &Tensor, weight_decay: f64) -> Result<f64> {
        self.network.train(states, actions, weight_decay)
    }
}

// Visualization Function
fn visualize_results(metrics: &[PerformanceMetrics], labels: &[&str]) -> Result<()> {
    let root = BitMapBackend::new("results.png", (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .caption("Regularization Methods Comparison", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..1000, -200.0..0.0)?;

    chart.configure_mesh().draw()?;

    for (i, metrics) in metrics.iter().enumerate() {
        chart
            .draw_series(LineSeries::new(
                metrics
                    .total_rewards
                    .iter()
                    .enumerate()
                    .map(|(x, y)| (x as i32, *y as f64)), // Convert rewards to `f64`
                &Palette99::pick(i),
            ))?
            .label(labels[i])
            .legend(move |(x, y)| {
                PathElement::new(vec![(x, y), (x + 20, y)], &Palette99::pick(i))
            });
    }

    chart
        .configure_series_labels()
        .border_style(&BLACK)
        .draw()?;

    Ok(())
}

// Main function to run experiments
fn main() -> Result<()> {
    let state_dim = 16;
    let action_dim = 16;
    let episodes = 1000;
    let max_steps = 200;

    let mut env = RLEnvironment::new(state_dim);

    let configs = [
        (0.0, 0.0, "No Regularization"),
        (0.01, 0.0, "L2 Regularization"),
        (0.0, 0.5, "Dropout"),
    ];

    let mut metrics_list = Vec::new();
    let mut labels = Vec::new();

    for &(weight_decay, dropout, label) in &configs {
        println!("Training configuration: {}", label);
        let mut agent = RLAgent::new(state_dim, action_dim, dropout);

        for episode in 0..episodes {
            env.reset();
            let mut total_reward = 0.0;
            let mut states = Vec::new();
            let mut actions = Vec::new();

            for _ in 0..max_steps {
                let state_tensor = Tensor::of_slice(&env.current_state)
                    .view([1, state_dim as i64])
                    .to_kind(Kind::Float);
                let action_tensor = agent.choose_action(&state_tensor);
                let action: Vec<f32> = action_tensor.view([-1]).try_into()?;
                let (_next_state, reward, done) = env.step(&action);

                total_reward += reward;
                states.push(state_tensor);
                actions.push(action_tensor);

                if done {
                    break;
                }
            }

            if !states.is_empty() {
                let states_tensor = Tensor::stack(&states, 0);
                let actions_tensor = Tensor::stack(&actions, 0);

                let loss = agent.train(&states_tensor, &actions_tensor, weight_decay)?;
                agent
                    .performance_metrics
                    .add_episode(total_reward, states.len(), loss);

                // Print important metrics every 100 episodes
                if episode % 100 == 0 {
                    println!(
                        "Episode {}: Total Reward: {:.2}, Loss: {:.6}",
                        episode, total_reward, loss
                    );
                }
            }
        }

        metrics_list.push(agent.performance_metrics);
        labels.push(label);
    }

    visualize_results(&metrics_list, &labels)?;
    Ok(())
}

The code defines a simulation environment and a feedforward neural network policy model. The model incorporates different configurations: no regularization, L2 regularization with a weight decay factor, and dropout with a specified probability. The training loop runs for 1000 episodes per configuration, collecting metrics like total rewards and losses after each episode. At the end of training, the results are visualized using the plotters crate, which plots the reward progression for each configuration, allowing a comparative analysis of their performance.

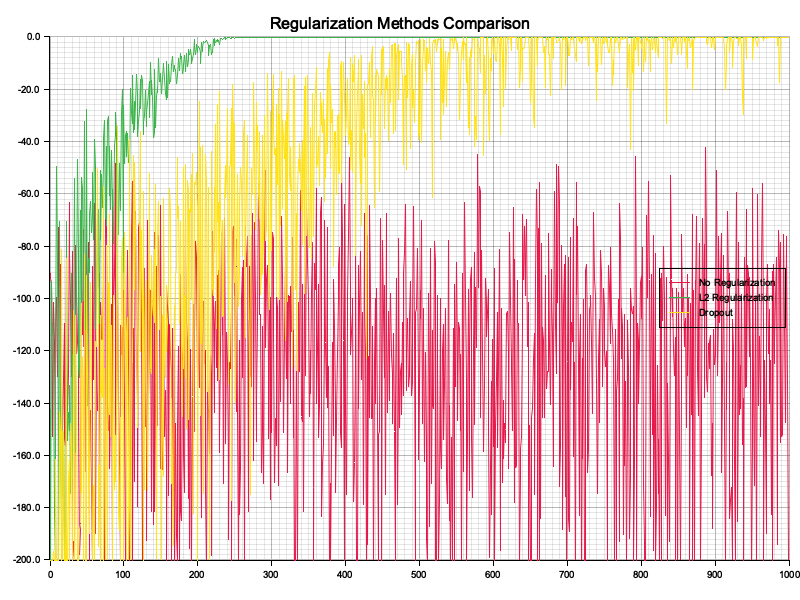
Figure 11: Plotters visualization of various regularization methods.

From the provided image, the "No Regularization" configuration (green) achieves faster convergence and higher overall rewards compared to the regularized models. However, the model with "L2 Regularization" (yellow) demonstrates more stable learning after an initial oscillation phase, suggesting that it helps in reducing overfitting and stabilizing rewards. The "Dropout" configuration (red) shows slower convergence and highly fluctuating rewards, indicating that dropout introduces significant noise during training, which may hinder rapid learning in this specific environment. Overall, L2 regularization seems to strike a good balance between stability and performance, while dropout's impact might require further parameter tuning.

Regularization is essential for building robust RL systems capable of generalizing across diverse environments. Techniques like L2 regularization, dropout, and batch normalization help constrain model complexity and improve adaptability. By implementing and visualizing these techniques in Rust, readers gain practical insights into how regularization enhances the performance and reliability of reinforcement learning agents in dynamic, real-world scenarios.

15.6. Trends and Future Directions in Deep Learning link

The rapid advancement of deep learning has profoundly transformed the field of reinforcement learning (RL), enabling agents to tackle complex decision-making tasks that were previously unattainable. Applications span diverse domains such as robotics, where agents learn to manipulate objects with dexterity; healthcare, where they assist in diagnosis and treatment planning; and autonomous systems, where they navigate dynamic environments with minimal human intervention. Despite these successes, RL faces significant challenges related to scalability, computational efficiency, and the integration of emerging paradigms in deep learning. Addressing these challenges is crucial for advancing the capabilities of RL agents and ensuring their practical applicability in real-world scenarios.

Figure 12: Common challenges in scaling RL models.

As deep learning models used in RL grow in complexity, their computational cost and energy requirements increase exponentially. Training large-scale models, such as Transformers with billions of parameters, demands advanced hardware and results in substantial energy consumption. This not only raises concerns about the environmental impact but also limits accessibility for researchers with limited computational resources. To mitigate these issues, there is a growing focus on developing techniques for parameter-efficient learning, such as model compression, pruning, and knowledge distillation. These methods aim to reduce the size of the models without compromising their performance, enabling more efficient training and inference.

Moreover, distributed training strategies are being employed to leverage parallel computing resources, reducing training time by distributing the workload across multiple processors or machines. Mathematical optimization techniques, such as synchronous and asynchronous gradient descent methods, are adapted to ensure convergence in distributed settings. Understanding the theoretical underpinnings of these methods is essential for designing algorithms that are both efficient and robust in large-scale training environments.

Another significant challenge in RL is the sparsity of data and reward signals. In many environments, rewards are delayed or occur infrequently, making gradient-based optimization methods inefficient due to high variance in the gradient estimates. This issue is exacerbated in environments with large state and action spaces, where exploring all possible states is computationally infeasible. Advanced techniques like reward shaping introduce additional informative signals to guide the learning process. Mathematically, reward shaping modifies the original reward function $R(s, a)$ to $R'(s, a) = R(s, a) + F(s, a, s')$, where $F$ is a potential-based function that depends on the current and next states, ensuring that the optimal policy remains unchanged while providing denser feedback.

Curiosity-driven exploration is another approach that encourages agents to explore novel states by incorporating an intrinsic reward signal based on the prediction error or uncertainty of the agent's model. This can be formalized by adding an intrinsic reward $r_t^{\text{int}} = \gamma \cdot \| \nabla_\theta L(\theta) \|$ to the extrinsic reward, where $L(\theta)$ is the loss function and $\gamma$ controls the influence of the intrinsic reward. Meta-learning, or "learning to learn," equips agents with the ability to rapidly adapt to new tasks or environments by leveraging prior experience, effectively reducing the data and time required for learning.

The advent of foundation models, such as GPT (Generative Pre-trained Transformer) and BERT (Bidirectional Encoder Representations from Transformers), has introduced new possibilities for scaling RL. These models are pre-trained on vast datasets to capture rich representations of the data domain, which can then be fine-tuned for specific tasks with relatively little additional data. In RL, foundation models can be integrated to enhance policy learning, especially in environments where understanding complex structures like language or code is essential. For instance, an RL agent equipped with a language model can interpret and follow natural language instructions, enabling more sophisticated interactions within its environment.

Few-shot learning extends this paradigm by enabling models to generalize from a minimal number of examples. In the context of RL, few-shot learning techniques allow agents to adapt quickly to new tasks with limited experience. Mathematically, this involves optimizing for a policy $\pi_\theta$ that minimizes the expected loss over a distribution of tasks $\mathcal{T}$:

$$ \min_\theta \mathbb{E}_{\tau \sim \mathcal{T}} \left[ L_\tau(\pi_\theta) \right], $$

where $L_\tau$ is the loss function for task $\tau$. By training over a variety of tasks, the agent learns a meta-policy that can be fine-tuned rapidly, reducing both data and computational demands.

Emerging trends in deep learning and RL also include the integration of graph neural networks (GNNs) and exploration into quantum computing. GNNs extend neural networks to process graph-structured data, which is prevalent in many RL applications involving relational data, such as social network interactions, transportation systems, or molecular structures. By representing the environment or the state space as a graph $G = (V, E)$, where $V$ is the set of nodes and $E$ is the set of edges, GNNs allow agents to reason about the relationships and dependencies between entities. This enhances the agent's ability to make decisions in highly interconnected environments.

Quantum computing represents a frontier in computational paradigms with the potential to exponentially accelerate optimization processes in RL. Quantum-inspired algorithms, such as quantum annealing and variational quantum circuits, can be used to explore large state spaces more efficiently than classical algorithms. While still in the early stages of development, quantum reinforcement learning offers promising directions for addressing computational bottlenecks in large-scale environments.

Implementing these advanced techniques and models poses challenges but also opportunities, particularly when utilizing a systems programming language like Rust. Rust provides memory safety guarantees without sacrificing performance, making it suitable for high-performance computing tasks required in RL. Rust's ownership model and concurrency features facilitate the development of efficient and reliable RL systems that can leverage distributed computing resources and manage complex data structures effectively.

In conclusion, the future of deep learning in reinforcement learning lies in overcoming scalability challenges and integrating emerging technologies to build more efficient, adaptable, and intelligent agents. By advancing parameter-efficient learning methods, leveraging foundation models for enhanced generalization, and exploring new computational paradigms like quantum computing, the RL community can push the boundaries of what is possible. Implementing these advancements in Rust not only contributes to performance and safety but also ensures that the development of RL systems remains at the forefront of technological innovation.

Rust, with its efficiency and safety, is an ideal language for experimenting with emerging trends in deep learning for RL. Below, we demonstrate two practical implementations: transfer learning with pre-trained models and self-supervised learning in RL environments.

The code below implements a reinforcement learning (RL) agent that learns to navigate a grid-based environment to reach a goal while avoiding obstacles. The environment is a simple 5x5 grid where the agent, obstacles, and the goal are randomly placed. The agent receives natural language instructions, which are processed using a pre-trained BERT model to extract meaningful features. These features are then passed through a policy network that outputs action probabilities, enabling the agent to decide its next move (up, down, left, or right) based on the instruction.

[dependencies]
anyhow = "1.0.94"
rand = "0.8.5"
rust-bert = "0.19.0"
serde_json = "1.0.133"
tch = "0.8.0"
reqwest = { version = "0.11", features = ["blocking"] }
rust_tokenizers = "8.1.1"

// Import necessary libraries and modules
use anyhow::{Result, Context};
use rand::Rng;
use rust_bert::bert::{BertModel, BertConfig, BertEmbeddings};
use rust_bert::Config; 
use rust_tokenizers::tokenizer::{BertTokenizer, Tokenizer, TruncationStrategy};
use std::path::Path;
use std::fs;
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Kind, Tensor};
use tch::nn::VarStore;
use reqwest::blocking::ClientBuilder;
use rust_tokenizers::vocab::Vocab;

/// Downloads BERT model files from Hugging Face and saves them to the specified directory.
///
/// # Arguments
///
/// * `model_dir` - A reference to a `Path` where the BERT model files will be stored.
///
/// # Returns
///
/// * `Result<()>` - Returns `Ok(())` if successful, or an `Err` containing the error details.
pub fn download_bert_resources(model_dir: &Path) -> Result<()> {
    fs::create_dir_all(model_dir)?;

    let model_resources = vec![
        (
            "https://huggingface.co/bert-base-uncased/resolve/main/config.json",
            model_dir.join("config.json"),
        ),
        (
            "https://huggingface.co/bert-base-uncased/resolve/main/pytorch_model.bin",
            model_dir.join("bert_model.bin"),
        ),
        (
            "https://huggingface.co/bert-base-uncased/resolve/main/vocab.txt",
            model_dir.join("vocab.txt"),
        ),
    ];

    let client = ClientBuilder::new()
        .timeout(None)
        .build()
        .with_context(|| "Failed to build HTTP client")?;

    for (url, filepath) in model_resources {
        if filepath.exists() {
            println!(
                "File {} already exists. Skipping download.",
                filepath.display()
            );
            continue;
        }

        println!("Downloading {} to {}", url, filepath.display());

        let mut response = client
            .get(url)
            .send()
            .with_context(|| format!("Failed to download from {}", url))?;

        if !response.status().is_success() {
            return Err(anyhow::anyhow!(
                "Failed to download file from {}: HTTP {}",
                url,
                response.status()
            ));
        }

        let mut dest = fs::File::create(&filepath)
            .with_context(|| format!("Failed to create file {}", filepath.display()))?;

        std::io::copy(&mut response, &mut dest).with_context(|| {
            format!(
                "Failed to write content to {}",
                filepath.display()
            )
        })?;
    }

    println!(
        "BERT model files downloaded successfully to {}",
        model_dir.display()
    );
    Ok(())
}

/// Represents the state of the agent in the grid environment.
#[derive(Clone, Debug, PartialEq)]
pub struct State {
    pub x: i32, // X-coordinate
    pub y: i32, // Y-coordinate
}

/// Represents the Reinforcement Learning environment with a grid, agent, goal, and obstacles.
#[derive(Debug)]
pub struct RLEnvironment {
    grid_size: i32,        // Size of the grid (grid_size x grid_size)
    agent_pos: State,      // Current position of the agent
    goal_pos: State,       // Position of the goal
    obstacles: Vec<State>, // Positions of the obstacles
    max_steps: i32,        // Maximum steps per episode
    current_step: i32,     // Current step count
}

impl RLEnvironment {
    /// Creates a new instance of the environment with random agent, goal, and obstacles.
    pub fn new() -> Self {
        let grid_size = 5; // 5x5 grid
        let mut rng = rand::thread_rng();

        // Randomly place agent
        let agent_pos = State { 
            x: rng.gen_range(0..grid_size), 
            y: rng.gen_range(0..grid_size) 
        };

        // Randomly place goal, ensuring it's not at the same position as the agent
        let mut goal_pos = agent_pos.clone();
        while goal_pos == agent_pos {
            goal_pos = State { 
                x: rng.gen_range(0..grid_size), 
                y: rng.gen_range(0..grid_size) 
            };
        }

        // Add random obstacles, ensuring they don't overlap with agent, goal, or other obstacles
        let mut obstacles = Vec::new();
        for _ in 0..3 {
            let mut obstacle = State { 
                x: rng.gen_range(0..grid_size), 
                y: rng.gen_range(0..grid_size) 
            };
            
            while obstacle == agent_pos || obstacle == goal_pos || obstacles.contains(&obstacle) {
                obstacle = State { 
                    x: rng.gen_range(0..grid_size), 
                    y: rng.gen_range(0..grid_size) 
                };
            }
            obstacles.push(obstacle);
        }

        Self {
            grid_size,
            agent_pos,
            goal_pos,
            obstacles,
            max_steps: 50,
            current_step: 0,
        }
    }

    /// Resets the environment to a new random state and returns the initial state of the agent.
    pub fn reset(&mut self) -> State {
        // Reinitialize the environment
        *self = Self::new();
        self.agent_pos.clone()
    }

    /// Takes an action in the environment and returns the new state, reward, and a boolean indicating if the episode is done.
    ///
    /// # Arguments
    ///
    /// * `action` - An integer representing the action (0: Up, 1: Right, 2: Down, 3: Left).
    ///
    /// # Returns
    ///
    /// * `(State, f64, bool)` - The new state, the reward received, and a boolean indicating if the episode is done.
    pub fn step(&mut self, action: i64) -> (State, f64, bool) {
        self.current_step += 1;

        // Determine new position based on action
        let mut new_pos = self.agent_pos.clone();
        match action {
            0 => new_pos.y = (new_pos.y - 1).max(0), // Up
            1 => new_pos.x = (new_pos.x + 1).min(self.grid_size - 1), // Right
            2 => new_pos.y = (new_pos.y + 1).min(self.grid_size - 1), // Down
            3 => new_pos.x = (new_pos.x - 1).max(0), // Left
            _ => {} // Invalid action, stay in place
        }

        // Check if new position is an obstacle
        let is_obstacle = self.obstacles.contains(&new_pos);

        // If new position is an obstacle, agent stays in the same place
        if is_obstacle {
            new_pos = self.agent_pos.clone();
        } else {
            self.agent_pos = new_pos.clone();
        }

        // Calculate reward
        let mut reward = -0.1; // Small negative reward for each step to encourage efficiency
        let is_goal = new_pos == self.goal_pos;
        
        if is_goal {
            reward = 10.0; // Large positive reward for reaching the goal
        }

        // Check if the episode is done
        let done = is_goal || self.current_step >= self.max_steps;

        (new_pos, reward, done)
    }

    /// Renders the current state of the environment to the console.
    pub fn render(&self) {
        for y in 0..self.grid_size {
            for x in 0..self.grid_size {
                if x == self.agent_pos.x && y == self.agent_pos.y {
                    print!("A "); // Agent
                } else if x == self.goal_pos.x && y == self.goal_pos.y {
                    print!("G "); // Goal
                } else if self.obstacles.iter().any(|obs| obs.x == x && obs.y == y) {
                    print!("X "); // Obstacle
                } else {
                    print!(". "); // Empty space
                }
            }
            println!();
        }
        println!();
    }
}

/// Feature extractor using a pre-trained BERT model.
struct BertFeatureExtractor {
    model: BertModel<BertEmbeddings>,
    tokenizer: BertTokenizer,
}

impl BertFeatureExtractor {
    /// Creates a new `BertFeatureExtractor` by loading the tokenizer and model configuration.
    ///
    /// # Arguments
    ///
    /// * `model_dir` - Path to the directory containing the BERT model files.
    ///
    /// # Returns
    ///
    /// * `Result<Self>` - Returns a new instance of `BertFeatureExtractor` or an error.
    fn new(model_dir: &Path) -> Result<Self> {
        // Load the tokenizer using rust_tokenizers
        let vocab_path = model_dir.join("vocab.txt");
        let tokenizer = BertTokenizer::from_file(
            vocab_path.to_str().unwrap(),
            false,
            false,
        ).map_err(|e| anyhow::anyhow!("Failed to load tokenizer: {}", e))?;

        // Load BERT configuration
        let config_path = model_dir.join("config.json");
        let config = BertConfig::from_file(config_path);

        // Create a variable store and initialize the BERT model
        let vs = VarStore::new(Device::Cpu);
        let model = BertModel::<BertEmbeddings>::new(&vs.root(), &config);

        Ok(Self { model, tokenizer })
    }

    /// Extracts features from the input text using the BERT model.
    ///
    /// # Arguments
    ///
    /// * `input` - The input text string.
    ///
    /// # Returns
    ///
    /// * `Result<Tensor>` - Returns the extracted features as a `Tensor`, or an error.
    fn extract_features(&self, input: &str) -> Result<Tensor> {
        // Tokenize the input text
        let tokens = self.tokenizer.encode(
            input,
            None,
            512, // Maximum sequence length
            &TruncationStrategy::LongestFirst,
            0,
        );
    
        // Convert tokens to tensors
        let input_ids = Tensor::of_slice(&tokens.token_ids).unsqueeze(0);
    
        // Obtain the padding token ID from the tokenizer's vocabulary
        let pad_id = self.tokenizer.vocab().token_to_id("[PAD]");
    
        // Generate attention mask
        let attention_mask_vec = tokens
            .token_ids
            .iter()
            .map(|&id| if id != pad_id { 1 } else { 0 }) // Both `id` and `pad_id` are `i64`
            .collect::<Vec<i64>>();
        let attention_mask = Tensor::of_slice(&attention_mask_vec).unsqueeze(0);
    
        // Forward pass through the BERT model
        let outputs = self.model.forward_t(
            Some(&input_ids),
            Some(&attention_mask),
            None,
            None,
            None,
            None,
            None,
            false,
        )?;
    
        // Extract the pooled output (CLS token representation)
        outputs
            .pooled_output
            .ok_or_else(|| anyhow::anyhow!("Failed to extract BERT features"))
    }
}

/// Policy network for the RL agent, implemented as a neural network.
#[derive(Debug)]
struct PolicyNetwork {
    fc: nn::Sequential,
}

impl PolicyNetwork {
    /// Creates a new `PolicyNetwork`.
    ///
    /// # Arguments
    ///
    /// * `input_dim` - The dimension of the input features.
    /// * `action_dim` - The number of possible actions.
    /// * `vs` - A reference to the variable store's root path.
    ///
    /// # Returns
    ///
    /// * `Self` - A new instance of `PolicyNetwork`.
    fn new(input_dim: i64, action_dim: i64, vs: &nn::Path) -> Self {
        let fc = nn::seq()
            .add(nn::linear(vs, input_dim, 128, Default::default()))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(vs, 128, action_dim, Default::default()));
        Self { fc }
    }
}

impl Module for PolicyNetwork {
    /// Forward pass through the policy network.
    ///
    /// # Arguments
    ///
    /// * `xs` - Input tensor.
    ///
    /// # Returns
    ///
    /// * `Tensor` - The output tensor after passing through the network.
    fn forward(&self, xs: &Tensor) -> Tensor {
        self.fc.forward(xs).softmax(-1, Kind::Float)
    }
}

/// The RL agent that interacts with the environment using a policy network and a feature extractor.
struct RLAgent {
    feature_extractor: BertFeatureExtractor,
    policy_network: PolicyNetwork,
    vs: nn::VarStore,
    optimizer: nn::Optimizer,
}

impl RLAgent {
    /// Creates a new `RLAgent`.
    ///
    /// # Arguments
    ///
    /// * `model_dir` - Path to the directory containing the BERT model files.
    ///
    /// # Returns
    ///
    /// * `Result<Self>` - Returns a new instance of `RLAgent` or an error.
    fn new(model_dir: &Path) -> Result<Self> {
        let vs = nn::VarStore::new(Device::Cpu);

        // Initialize the feature extractor
        let feature_extractor = BertFeatureExtractor::new(model_dir)?;

        // Initialize the policy network
        let policy_network = PolicyNetwork::new(
            768, // BERT CLS token dimension
            4,   // Number of grid actions (Up, Right, Down, Left)
            &vs.root(),
        );

        // Initialize the optimizer
        let optimizer = nn::Adam::default().build(&vs, 1e-4)?;

        Ok(Self {
            feature_extractor,
            policy_network,
            vs,
            optimizer,
        })
    }
    
    /// Trains the agent using the collected log probabilities and rewards.
    ///
    /// # Arguments
    ///
    /// * `log_probs` - A slice of log probability tensors from the policy network.
    /// * `rewards` - A slice of rewards obtained during the episode.
    ///
    /// # Returns
    ///
    /// * `Result<()>` - Returns `Ok(())` if training succeeds, or an error.
    fn train(&mut self, log_probs: &[Tensor], rewards: &[f64]) -> Result<()> {
        // Compute discounted rewards
        let mut discounted_rewards = Vec::new();
        let mut cumulative_reward = 0.0;
    
        for &reward in rewards.iter().rev() {
            cumulative_reward = reward + cumulative_reward * 0.99; // Discount factor
            discounted_rewards.insert(0, cumulative_reward);
        }
    
        // Normalize rewards
        let rewards_tensor = Tensor::of_slice(&discounted_rewards).to_kind(Kind::Float);
        let mean_reward = rewards_tensor.mean(Kind::Float);
        let std_reward = rewards_tensor.std(true);
        let normalized_rewards = (rewards_tensor - mean_reward) / (std_reward + 1e-9);
    
        // Compute loss
        let log_probs_tensor = Tensor::stack(log_probs, 0);
        let loss = -(log_probs_tensor.squeeze() * normalized_rewards).mean(Kind::Float);
    
        // Log the loss value
        println!("Loss: {:?}", loss.double_value(&[]));
    
        // Backpropagation
        self.optimizer.zero_grad();
        loss.backward();
    
        // Gradient clipping
        for (name, var) in self.vs.variables() {
            if var.requires_grad() {
                let grad = var.grad();
                let grad_norm = grad.norm().double_value(&[]);
                // Log gradient norms
                println!("Gradient Norm for {}: {}", name, grad_norm);
    
                // Gradient clipping
                let clipped_grad = grad.clamp(-1.0, 1.0);
                var.grad().copy_(&clipped_grad);
            }
        }
    
        // Update parameters
        self.optimizer.step();
        Ok(())
    }
            
    /// Chooses an action based on the given instruction using the policy network.
    ///
    /// # Arguments
    ///
    /// * `instruction` - A string instruction for the agent.
    ///
    /// # Returns
    ///
    /// * `Result<(i64, Tensor)>` - Returns the chosen action and its log probability, or an error.
    fn choose_action(&self, instruction: &str) -> Result<(i64, Tensor)> {
        // Extract features from the instruction
        let features = self.feature_extractor.extract_features(instruction)?;
        let probs = self.policy_network.forward(&features);
    
        // Check for NaN or Inf in probs
        if probs.f_isnan()?.any().int64_value(&[]) != 0 || probs.f_isinf()?.any().int64_value(&[]) != 0 {
            println!("Warning: probs contains NaN or Inf");
            println!("probs: {:?}", probs);
        }
    
        // Ensure probabilities sum to 1
        let sum_probs = probs.sum(Kind::Float).double_value(&[]);
        if (sum_probs - 1.0).abs() > 1e-6 {
            println!("Warning: Probabilities do not sum to 1. Sum: {}", sum_probs);
        }
    
        // Log the action probabilities
        println!("Action Probabilities: {:?}", probs);
    
        // Sample an action from the probability distribution
        let action = probs.multinomial(1, true);
        let prob = probs.gather(1, &action, false);
    
        // Log the selected action
        println!("Selected Action: {}", action.int64_value(&[]));
    
        // Calculate log probability for loss computation
        let log_prob = prob.log();
    
        Ok((action.int64_value(&[]), log_prob))
    }    
}

/// Main function that runs the training loop for the RL agent.
fn main() -> Result<()> {
    // Define the directory where model files will be stored
    let model_dir = Path::new("./bert_model");

    // Download BERT resources before initializing the agent
    download_bert_resources(model_dir)?;

    // Initialize agent and environment
    let mut agent = RLAgent::new(model_dir)?;
    let mut env = RLEnvironment::new();

    let episodes = 1000;
    for episode in 0..episodes {
        let _state = env.reset();
        let mut done = false;
        let mut log_probs = Vec::new();
        let mut rewards = Vec::new();

        while !done {
            let instruction = "Navigate to the goal position.";
            let (action, log_prob) = agent.choose_action(instruction)?;
            let (_, reward, episode_done) = env.step(action);

            // Optionally render the environment during training
            // env.render();

            log_probs.push(log_prob);
            rewards.push(reward);

            done = episode_done;
        }

        // Train the agent after each episode
        agent.train(&log_probs, &rewards)?;
        println!("Episode {}: Total Reward: {}", episode + 1, rewards.iter().sum::<f64>());
    }

    Ok(())
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    /// Tests the basic functionality of the environment.
    fn test_environment_basic_functionality() {
        let mut env = RLEnvironment::new();
        
        // Test reset
        let initial_state = env.reset();
        assert!(initial_state.x >= 0 && initial_state.x < 5);
        assert!(initial_state.y >= 0 && initial_state.y < 5);

        // Test step
        let (new_state, _reward, done) = env.step(1); // Move right
        assert!(!done);
        assert!(new_state.x >= 0 && new_state.x < 5);
        assert!(new_state.y >= 0 && new_state.y < 5);
        
        // Render for visual debugging
        env.render();
    }
}

In detail, the RLEnvironment simulates the grid world, providing methods to reset and step through the environment. The BertFeatureExtractor uses BERT to convert the instruction "Navigate to the goal position." into a feature vector representing the semantic meaning of the instruction. The PolicyNetwork is a simple neural network that takes the BERT features as input and produces a log-probability distribution over possible actions using a log-softmax activation. The RLAgent combines these components, choosing actions based on the policy network's output and learning from the rewards received by updating the network's parameters using policy gradient methods.

This integration of natural language processing and reinforcement learning allows the agent to interpret and act upon textual instructions, showcasing how advanced language models like BERT can enhance the capabilities of RL agents. By leveraging pre-trained language models, the agent can understand complex instructions and potentially adapt to a variety of tasks without task-specific programming. This approach demonstrates the potential for creating intelligent systems that can interact more naturally with humans, bridging the gap between language understanding and action in an environment.

Lets learn from other implementation of self-supervised learning that introduces auxiliary tasks to augment sparse reward signals. Here, we implement a prediction task where the agent learns to predict future states. The SSL code integrates a reinforcement learning setup where an agent learns to interact with an environment through self-supervised tasks. It uses a policy network to generate actions and a prediction network to model the next state given the current state and action. The agent optimizes its policy and prediction tasks simultaneously using a combination of policy rewards and auxiliary prediction losses. The environment provides sparse rewards based on the agent's actions, and the training loop iteratively updates the agent's neural networks to improve its performance.

use anyhow::Result;
use ndarray::Array1;
use plotters::prelude::*;
use rand::distributions::{Distribution, Uniform};
use tch::{nn, nn::{Module, OptimizerConfig}, Device, Tensor};

// Environment
struct SimpleEnvironment {
    state_dim: usize,
    state: Array1<f32>,
}

impl SimpleEnvironment {
    fn new(state_dim: usize) -> Self {
        let mut env = SimpleEnvironment {
            state_dim,
            state: Array1::zeros(state_dim),
        };
        env.reset();
        env
    }

    fn reset(&mut self) -> Array1<f32> {
        let mut rng = rand::thread_rng();
        let between = Uniform::new(-1.0, 1.0);
        self.state = Array1::from_vec(
            (0..self.state_dim)
                .map(|_| between.sample(&mut rng))
                .collect()
        );
        self.state.clone()
    }

    fn step(&mut self, action: &Array1<f32>) -> (Array1<f32>, f32, bool) {
        // Update state
        let next_state = &self.state + &(action * 0.1);
        
        // Compute reward (sparse reward based on action)
        let reward = -action.iter().map(|&x| (x - 0.5).powi(2)).sum::<f32>().sqrt();
        
        // Check if episode is done
        let done = next_state.mapv(|x| x.powi(2)).sum().sqrt() > 2.0;
        
        // Update state
        self.state = if done { 
            Array1::zeros(self.state_dim) 
        } else { 
            next_state.clone() 
        };

        (self.state.clone(), reward, done)
    }
}

// Self-Supervised Agent
struct SelfSupervisedAgent {
    vs: nn::VarStore,
    policy_net: nn::Sequential,
    prediction_net: nn::Sequential,
}

impl SelfSupervisedAgent {
    fn new(state_dim: usize, action_dim: usize, hidden_dim: usize) -> Self {
        let vs = nn::VarStore::new(Device::Cpu);
        let root = vs.root();

        let policy_net = nn::seq()
            .add(nn::linear(
                root.clone() / "policy_fc1", 
                state_dim as i64, 
                hidden_dim as i64, 
                Default::default()
            ))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(
                root.clone() / "policy_fc2", 
                hidden_dim as i64, 
                action_dim as i64, 
                Default::default()
            ));

        let prediction_net = nn::seq()
            .add(nn::linear(
                root.clone() / "pred_fc1", 
                (state_dim + action_dim) as i64, 
                hidden_dim as i64, 
                Default::default()
            ))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(
                root.clone() / "pred_fc2", 
                hidden_dim as i64, 
                state_dim as i64, 
                Default::default()
            ));

        SelfSupervisedAgent {
            vs,
            policy_net,
            prediction_net,
        }
    }

    fn forward(&self, state: &Tensor) -> Tensor {
        self.policy_net.forward(state)
    }

    fn predict_next_state(&self, state: &Tensor, action: &Tensor) -> Tensor {
        let input = Tensor::cat(&[state, action], 1);
        self.prediction_net.forward(&input)
    }
}

// Environment and Agent Definitions Remain Unchanged

fn train_self_supervised_agent() -> Result<()> {
    // Hyperparameters
    let state_dim = 4;
    let action_dim = 4;
    let hidden_dim = 64;
    let num_episodes = 1000;
    let max_steps = 100;

    // Initialize environment and agent
    let mut env = SimpleEnvironment::new(state_dim);
    let agent = SelfSupervisedAgent::new(state_dim, action_dim, hidden_dim);
    
    // Optimizer
    let mut optimizer = nn::Adam::default().build(&agent.vs, 1e-3)?;

    // Data for visualization
    let mut rewards: Vec<f64> = Vec::new();
    let mut losses: Vec<f64> = Vec::new();

    // Training loop
    for episode in 0..num_episodes {
        // Reset environment
        let state = env.reset(); 
        let mut state_tensor = Tensor::of_slice(state.to_vec().as_slice()).unsqueeze(0);
        
        let mut episode_reward = 0.0;
        let mut prediction_loss = 0.0;
        let mut last_step = 0;

        for step in 0..max_steps {
            // Get action from policy network
            let action_tensor = agent.forward(&state_tensor);
            let action: Vec<f32> = action_tensor.squeeze_dim(0).to_kind(tch::Kind::Float).view([-1]).try_into()?; 
            
            // Step in the environment
            let (next_state, reward, done) = env.step(&Array1::from_vec(action.clone()));
            
            // Convert to tensors
            let next_state_tensor = Tensor::of_slice(next_state.to_vec().as_slice()).unsqueeze(0);
            let action_tensor = Tensor::of_slice(action.as_slice()).unsqueeze(0);
            
            // Compute prediction loss (auxiliary task)
            let next_state_pred = agent.predict_next_state(&state_tensor, &action_tensor);
            let pred_loss = next_state_pred.mse_loss(&next_state_tensor, tch::Reduction::Mean);
            
            // Compute policy loss (simplified)
            let policy_loss = Tensor::of_slice(&[-reward]);
            
            // Total loss
            let loss = pred_loss.shallow_clone() + policy_loss; 
            optimizer.zero_grad();
            loss.backward();
            optimizer.step();
            
            // Update for next step
            state_tensor = next_state_tensor;
            episode_reward += reward;
            prediction_loss += pred_loss.double_value(&[]); 
            last_step = step;
            
            if done {
                break;
            }
        }

        rewards.push(episode_reward as f64);
        losses.push(prediction_loss / (last_step + 1) as f64);

        println!(
            "Episode {}: Reward = {:.2}, Prediction Loss = {:.4}",
            episode + 1,
            episode_reward,
            prediction_loss / (last_step + 1) as f64
        );
    }

    // Visualize results
    plot_results(&rewards, &losses)?;

    Ok(())
}

fn plot_results(rewards: &[f64], losses: &[f64]) -> Result<()> {
    let root_area = BitMapBackend::new("training_results.png", (1024, 768)).into_drawing_area();
    root_area.fill(&WHITE)?;

    let (upper, lower) = root_area.split_vertically(384);

    // Plot rewards
    let mut rewards_chart = ChartBuilder::on(&upper)
        .caption("Rewards per Episode", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..rewards.len(), *rewards.iter().min_by(|a, b| a.partial_cmp(b).unwrap()).unwrap()..*rewards.iter().max_by(|a, b| a.partial_cmp(b).unwrap()).unwrap())?;
    
    rewards_chart.configure_mesh().draw()?;
    rewards_chart.draw_series(LineSeries::new(
        rewards.iter().enumerate().map(|(x, &y)| (x, y)),
        &BLUE,
    ))?;

    // Plot losses
    let mut losses_chart = ChartBuilder::on(&lower)
        .caption("Prediction Loss per Episode", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..losses.len(), *losses.iter().min_by(|a, b| a.partial_cmp(b).unwrap()).unwrap()..*losses.iter().max_by(|a, b| a.partial_cmp(b).unwrap()).unwrap())?;
    
    losses_chart.configure_mesh().draw()?;
    losses_chart.draw_series(LineSeries::new(
        losses.iter().enumerate().map(|(x, &y)| (x, y)),
        &RED,
    ))?;

    Ok(())
}

fn main() -> Result<()> {
    train_self_supervised_agent()
}

The program consists of three main components: the environment, the agent, and the training loop. The environment represents a simple state-action space, where the agent interacts by taking actions and receiving rewards and next states. The agent has two neural networks: the policy network, which predicts the best action for a given state, and the prediction network, which predicts the next state. During training, the agent steps through the environment, generating actions and calculating the total loss (composed of policy and prediction losses). The agent uses the Adam optimizer to minimize the loss and improve its policy and prediction accuracy over episodes.

Figure 13: Plotters visualization of reward and loss per episode.

The reward and prediction loss metrics were visualized using line plots. The reward plot (upper graph) shows the agent's total reward per episode, indicating how well the agent performs in the environment. A fluctuating reward pattern suggests the agent's actions are continually adapting, with rewards varying based on the environment's conditions. The loss plot (lower graph) tracks the prediction loss over episodes, starting high and gradually decreasing as the agent becomes better at predicting next states. This downward trend highlights the agent's improvement in its auxiliary self-supervised task over time.

The future of deep learning in RL lies in addressing the challenges of scaling, integrating novel paradigms like foundation models and quantum computing, and leveraging emerging techniques such as self-supervised learning and transfer learning. By experimenting with these approaches in Rust, readers can develop efficient and scalable RL systems, staying at the forefront of this rapidly evolving field. Rust's performance and safety features make it an excellent choice for pushing the boundaries of RL research and applications.

15.7. Conclusion link

Deep learning has become an essential enabler of reinforcement learning, expanding its potential to solve high-dimensional, dynamic, and collaborative problems across diverse domains. Chapter 15 encapsulates this synergy by exploring the mathematical foundations, architectural advancements, and practical implementations of deep learning within RL. Through an in-depth discussion of neural network models, optimization techniques, and scalable frameworks like Transformers, it equips readers with the tools to design sophisticated systems that push the boundaries of what RL can achieve. With practical examples implemented in Rust, the chapter bridges the gap between theoretical understanding and real-world application, positioning deep learning as the cornerstone of future innovations in reinforcement learning.

15.7.1. Further Learning with GenAI link

These prompts are carefully designed to explore the intersection of deep learning and reinforcement learning (RL), emphasizing both theoretical depth and practical expertise. They guide learners through foundational concepts like feedforward networks, convolutional architectures, and recurrent models while introducing cutting-edge advancements such as attention mechanisms, Transformers, and optimization strategies tailored for RL tasks.

• Explain the fundamentals of deep learning: What is the mathematical basis of neural networks as universal function approximators, and how does their hierarchical structure facilitate representation learning? Implement a feedforward neural network in Rust using the tch crate, and demonstrate its ability to approximate non-linear functions.

• Discuss depth in neural networks: How does increasing the depth of a network affect its expressive power, optimization, and generalization in reinforcement learning tasks? Implement a deep network in Rust for policy approximation and analyze its performance with varying depths on a control task.

• Analyze activation functions in depth: How do activation functions like ReLU, Sigmoid, Tanh, GELU, and Swish impact gradient flow, convergence, and representational power in RL tasks? Implement these functions in Rust, compare their behaviors on synthetic data, and evaluate their effect on training an RL agent.

• Explore optimization techniques: What are the theoretical underpinnings of optimizers like SGD, Adam, and RMSProp, and how do they address challenges like vanishing gradients and sparse rewards in RL? Implement these optimizers in Rust and demonstrate their convergence properties on a policy gradient problem.

• Examine the architecture of feedforward networks: How do dense layers map input features to higher-dimensional representations, and why are they effective for reinforcement learning tasks like policy and value function approximation? Build and train a feedforward neural network in Rust for an RL problem, analyzing its performance.

• Analyze convolutional networks (CNNs) for RL: How do CNNs leverage spatial hierarchies for feature extraction, and why are they particularly suited for visual RL tasks like game-playing? Implement a CNN in Rust for an Atari-like environment and demonstrate its ability to learn spatially correlated features.

• Explore recurrent networks (RNNs) and LSTMs in RL: How do RNNs and LSTMs model temporal dependencies, and what advantages do they offer for sequential decision-making in RL tasks? Implement an LSTM in Rust and evaluate its performance on a time-series RL task.

• Discuss the importance of attention mechanisms in RL: What is the mathematical formulation of self-attention, and how does it improve scalability and efficiency in RL tasks? Implement an attention-based model in Rust and demonstrate its utility in multi-agent coordination or memory-based tasks.

• Examine Transformers in RL systems: How do Transformers handle long-range dependencies and parallelize computations, making them suitable for large-scale RL problems? Implement a Transformer in Rust and compare its performance against traditional recurrent architectures in an RL task.

• Discuss the role of regularization in RL: How do regularization techniques like Dropout, Batch Normalization, and entropy regularization enhance generalization and stability in RL? Implement these techniques in Rust and evaluate their impact on overfitting and exploration in a noisy RL environment.

• Analyze the importance of entropy regularization: How does entropy regularization encourage exploration in policy-based RL methods, and how can it be tuned for effective performance? Implement entropy regularization in Rust for a policy gradient method and analyze its effect on exploration in sparse-reward tasks.

• Compare deep learning frameworks for RL: What are the strengths and weaknesses of PyTorch, TensorFlow, and Rust’s tch for deep reinforcement learning? Build a simple pipeline in Rust and compare its performance and efficiency to a PyTorch-based implementation.

• Integrate deep learning with reinforcement learning: How do architectures like deep Q-networks (DQNs) and actor-critic models use deep learning to solve RL tasks? Implement a DQN in Rust for a discrete action-space problem and analyze its convergence properties.

• Explore self-supervised learning in RL: How does pretraining with auxiliary tasks improve sample efficiency in RL environments with sparse rewards? Implement a self-supervised learning setup in Rust for a sparse-reward RL environment and evaluate its effectiveness.

• Analyze transfer learning in deep RL: How does transfer learning accelerate learning for new RL tasks, and what are the best practices for fine-tuning pre-trained models? Implement transfer learning in Rust using a pre-trained CNN for a visual RL problem and evaluate its efficiency.

• Discuss Transformers as foundation models for RL: How can pre-trained Transformers be adapted for reinforcement learning, and what challenges arise in their application to RL tasks? Fine-tune a pre-trained Transformer in Rust for a language-based RL problem and analyze its adaptability.

• Examine hierarchical policies in RL: How do hierarchical architectures optimize multi-level tasks in RL, and what advantages do they offer for complex environments? Implement a hierarchical policy framework in Rust for a multi-level logistics optimization problem and evaluate its performance.

• Explore sparsity and robustness in deep RL: How do sparsity-inducing techniques like pruning and quantization enhance model efficiency, and how do they impact performance in real-world RL tasks? Implement these techniques in Rust for a lightweight RL model and evaluate their effect on efficiency and accuracy.

• Discuss scalability challenges in RL systems: How do techniques like parallelization, distributed training, and asynchronous updates improve the scalability of RL algorithms in large environments? Implement a parallelized RL framework in Rust using the rayon crate and test its scalability on a large-scale task.

• Analyze the future of deep learning in RL: How are trends like meta-learning, hybrid models, and foundation architectures shaping the future of reinforcement learning? Implement a meta-learning-based RL framework in Rust and evaluate its ability to adapt to dynamic, multi-task environments.

These prompts aim to deepen your understanding of the foundational and advanced aspects of deep learning for reinforcement learning. By exploring theoretical principles, state-of-the-art architectures, and practical Rust-based implementations, these prompts encourage you to build efficient, scalable, and cutting-edge RL systems using deep learning techniques.

15.7.2. Hands on Practices link

These exercises provide hands-on opportunities to experiment with deep learning techniques, explore their integration with reinforcement learning, and develop practical Rust-based implementations. By engaging with these tasks, readers will strengthen their understanding of neural network architectures, optimization strategies, and advanced applications.

Exercise 15.1: Building a Feedforward Neural Network in Rust link

Task:\ Develop a feedforward neural network using the tch crate in Rust. Train the network to approximate a simple non-linear function (e.g., $y = \sin(x)$) using synthetic data.

Challenge:\ Experiment with different depths and activation functions (ReLU, Tanh, Sigmoid) to observe their effects on training convergence and accuracy. Visualize the network’s predictions and training loss using a Rust plotting library.

Exercise 15.2: Implementing a Convolutional Neural Network for Image Classification link

Task:\ Create a convolutional neural network (CNN) in Rust for image classification on a small dataset, such as MNIST. Include convolutional, pooling, and fully connected layers in the architecture.

Challenge:\ Experiment with data augmentation techniques like rotation and scaling to improve generalization. Analyze the impact of varying kernel sizes, pooling methods, and dropout rates on classification accuracy.

Exercise 15.3: Training an LSTM for Sequence Prediction link

Task:\ Build and train a Long Short-Term Memory (LSTM) network in Rust for a sequence prediction task, such as predicting the next value in a sine wave series.

Challenge:\ Experiment with different LSTM configurations, such as the number of hidden units and sequence lengths, to optimize prediction accuracy. Compare the performance of the LSTM to a feedforward network on the same task.

Exercise 15.4: Implementing an Attention-Based Network for Reinforcement Learning link

Task:\ Develop an attention-based network in Rust for a reinforcement learning environment where the agent must focus on relevant parts of the state space (e.g., a grid-world navigation task with distractors).

Challenge:\ Experiment with self-attention and multi-head attention mechanisms to improve the agent’s learning efficiency. Visualize the attention weights to understand which state features the model prioritizes during decision-making.

Exercise 15.5: Fine-Tuning a Pre-Trained Transformer for RL Tasks link

Task:\ Fine-tune a pre-trained Transformer model in Rust for a reinforcement learning task, such as language-based navigation or goal-setting in a text-based environment.

Challenge:\ Incorporate transfer learning to leverage the Transformer’s pre-trained capabilities and adapt it to the RL task. Compare the performance and sample efficiency of the Transformer against a traditional recurrent network.

By engaging with these hands-on practices, you will gain a deeper understanding of the foundational principles and advanced applications of deep learning. These exercises will empower you to implement state-of-the-art architectures in Rust and explore their potential for solving real-world challenges with reinforcement learning.