16.1. Introduction to Deep Reinforcement Learning link

In the realm of complex decision-making tasks, Deep Reinforcement Learning (DRL) stands out as a powerful methodology that seamlessly integrates the representational capacity of deep learning with the decision-making framework of reinforcement learning. Traditional reinforcement learning (RL) techniques, while theoretically sound and effective in certain domains, often falter when faced with environments featuring high-dimensional state spaces—think of raw image inputs or intricate continuous action domains. DRL tackles this challenge by embedding the learning process within deep neural networks, allowing an agent to learn directly from raw inputs such as pixels, sound waves, or sensor readings, thereby extending RL methods to problems that were previously intractable.

At the heart of DRL lies the idea of function approximation. In classical RL, value functions $V^\pi(s)$ or action-value functions $Q^\pi(s,a)$ could be represented exactly for small state spaces, but this becomes unfeasible as the dimensionality grows. Instead, we use deep neural networks as powerful parametric function approximators. For example, if our agent follows a policy $\pi$, the action-value function $Q^\pi(s,a)$ is defined as the expected return starting from state $s$, taking action $a$, and thereafter following policy $\pi$. Formally, this is $Q^\pi(s,a) = \mathbb{E}[R_t \mid S_t = s, A_t = a, \pi]$, where $R_t = \sum_{k=0}^{\infty} \gamma^k r_{t+k+1}$ and $\gamma \in [0,1]$ is a discount factor controlling the trade-off between immediate and long-term rewards. In DRL, we approximate $Q^\pi(s,a)$ using a neural network $Q(s,a;\theta)$ with parameters $\theta$. By adjusting $\theta$ through stochastic gradient descent and backpropagation, we find a parameterization of the network that captures complex relationships between states, actions, and future returns.

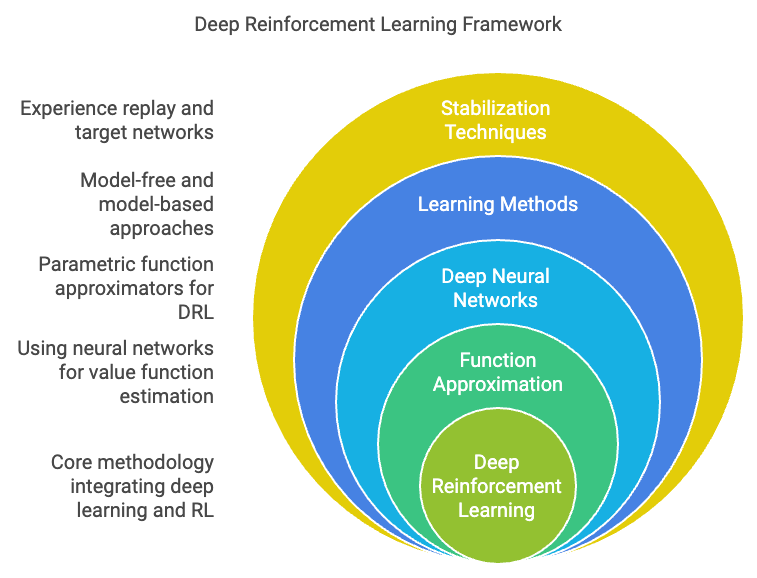
Figure 1: Scopes and taxonomy of DRL framework.

Deep learning’s capacity to process raw, unstructured data allows DRL algorithms to scale gracefully. Instead of manually engineering features or relying on heavily pre-processed inputs, DRL methods learn representations directly from high-dimensional observations. For instance, in a game like Pong, raw pixel data is fed into a convolutional neural network that extracts meaningful features—edges, shapes, ball positions, and paddles—from which the network can then learn optimal actions. This synergy dramatically simplifies the pipeline, as the network itself discovers which features matter most for decision-making.

When discussing DRL, it is crucial to differentiate between model-free and model-based approaches. Model-free methods, such as Deep Q-Networks (DQN) or policy gradient methods, do not attempt to estimate the underlying dynamics of the environment. Instead, they directly learn value functions or policies that map states to actions. This can be advantageous when the environment is complex or partially observable, as building an internal model might be too challenging or resource-intensive. On the other hand, model-based approaches try to construct an approximate model of the environment’s dynamics: if we denote the environment’s transition probability as $P(s'|s,a)$ and the reward function as $R(s,a)$, a model-based method attempts to learn or leverage these to plan ahead. While model-based DRL can be more sample-efficient and capable of simulating future scenarios, it also introduces complexity in model learning and planning. Understanding when and how to leverage model-based methods often depends on the particular characteristics of the task at hand, such as whether a known or easily approximable dynamics model exists.

One of the key techniques enabling stable deep Q-learning involves two innovations: experience replay and target networks. Experience replay breaks the correlation of sequential data by storing past transitions $(s,a,r,s')$ in a replay buffer and sampling mini-batches uniformly or according to a priority scheme. This stabilizes learning by preventing the network from overfitting to recent samples and encourages reuse of past experiences. Target networks further stabilize learning by maintaining a separate set of parameters $\theta^-$ for the target Q-network. Rather than updating both the main Q-network and the target Q-network simultaneously, we periodically copy the weights of the main Q-network to the target network. This simple technique avoids the rapid oscillations or divergence that can occur when the Q-network tries to predict targets that are themselves rapidly changing. In more detail, a hallmark of DRL is its ability to stabilize training through techniques like experience replay and target networks:

• Experience Replay: The agent stores transitions $(s, a, r, s')$ in a replay buffer, which it samples uniformly or with priority during training. This technique reduces the correlation between consecutive samples and ensures better coverage of the state-action space.

• Target Networks: In DQNs, target values for the Bellman equation are calculated using a periodically updated target network $Q_{\text{target}}(s, a; \theta^-)$. By decoupling the updates of the target and primary networks, this approach mitigates instability caused by rapidly changing target values.

Balancing exploration and exploitation becomes even more nuanced in deep RL. Agents must occasionally choose actions at random (exploration) to discover new states and strategies, while also leveraging their learned Q-values or policies (exploitation) to maximize long-term returns. With large or continuous action spaces, classical methods like $\epsilon$-greedy exploration may be insufficient. Instead, DRL practitioners might use noise processes added to policy outputs or parameterized exploration methods. The essence remains the same: find a suitable equilibrium that leads to efficient learning and good long-term performance.

Balancing exploration (searching for new actions) and exploitation (choosing the best-known action) is fundamental to DRL. High-dimensional environments exacerbate this trade-off, necessitating sophisticated strategies like:

• Entropy Regularization: Encouraging stochastic policies by adding entropy to the loss function.

• Parameterized Noise: Injecting noise into policy parameters to encourage exploration.

• Curiosity-Driven Exploration: Augmenting rewards with intrinsic signals based on novelty.

On a practical level, implementing a Deep Q-Network in Rust can be achieved using ecosystem crates for machine learning and numeric computing. Although Rust’s deep learning stack is still growing, we can leverage crates like tch (Rust bindings for PyTorch) to build neural networks, or ndarray for numeric manipulations. The DQN experiment implemented here simulates reinforcement learning using two network architectures: a Multi-Layer Perceptron (MLP) and a Convolutional Neural Network (CNN). Both networks act as Q-value approximators to estimate the action-value function in a discrete environment. The experiment uses a replay buffer to store transitions (state, action, reward, next_state, done) collected from the environment. During training, these transitions are sampled randomly to break correlation between experiences, ensuring better convergence. The primary goal is to evaluate the learning performance of MLP and CNN architectures by comparing their rewards over epochs.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use tch::{nn, nn::ModuleT, Device, Tensor, Kind, Reduction};
use tch::nn::OptimizerConfig;
use rand::Rng;
use plotters::prelude::*;

// Base QNetwork trait for common interface
trait QNetworkTrait {
    fn forward(&self, state: &Tensor) -> Tensor;
    fn get_varstore(&self) -> &nn::VarStore;
}

// MLP Network Architecture
struct MLPNetwork {
    vs: nn::VarStore,
    net: nn::Sequential,
}

impl QNetworkTrait for MLPNetwork {
    fn forward(&self, state: &Tensor) -> Tensor {
        self.net.forward_t(state, false)
    }

    fn get_varstore(&self) -> &nn::VarStore {
        &self.vs
    }
}

impl MLPNetwork {
    fn new(device: Device, input_dim: i64, action_dim: i64) -> Self {
        let vs = nn::VarStore::new(device);
        let net = nn::seq()
            .add(nn::linear(&vs.root(), input_dim, 128, Default::default()))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(&vs.root(), 128, 64, Default::default()))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(&vs.root(), 64, action_dim, Default::default()));

        MLPNetwork { vs, net }
    }
}

// CNN Network Architecture
struct CNNNetwork {
    vs: nn::VarStore,
    net: nn::Sequential,
}

impl QNetworkTrait for CNNNetwork {
    fn forward(&self, state: &Tensor) -> Tensor {
        self.net.forward_t(state, false)
    }

    fn get_varstore(&self) -> &nn::VarStore {
        &self.vs
    }
}

impl CNNNetwork {
    fn new(device: Device, input_channels: i64, input_height: i64, input_width: i64, action_dim: i64) -> Self {
        let vs = nn::VarStore::new(device);
        let root = vs.root();

        let net = nn::seq()
            .add(nn::conv2d(&root, input_channels, 32, 3, Default::default()))
            .add_fn(|x| x.relu())
            .add_fn(|x| x.max_pool2d_default(2))
            .add(nn::conv2d(&root, 32, 64, 3, Default::default()))
            .add_fn(|x| x.relu())
            .add_fn(|x| x.max_pool2d_default(2))
            .add_fn(|x| x.flatten(1, -1))
            .add(nn::linear(&root, 64 * ((input_height / 4 - 1) * (input_width / 4 - 1)), 128, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 128, action_dim, Default::default()));

        CNNNetwork { vs, net }
    }
}

// Replay Buffer
struct ReplayBuffer {
    states: Vec<Tensor>,
    actions: Vec<i64>,
    rewards: Vec<f32>,
    next_states: Vec<Tensor>,
    dones: Vec<bool>,
}

impl ReplayBuffer {
    fn new() -> Self {
        ReplayBuffer {
            states: Vec::new(),
            actions: Vec::new(),
            rewards: Vec::new(),
            next_states: Vec::new(),
            dones: Vec::new(),
        }
    }

    fn sample(&self, batch_size: usize) -> (Tensor, Tensor, Tensor, Tensor, Tensor) {
        let mut rng = rand::thread_rng();
        let idxs: Vec<_> = (0..batch_size).map(|_| rng.gen_range(0..self.states.len())).collect();
        let states = Tensor::stack(&idxs.iter().map(|&i| &self.states[i]).collect::<Vec<_>>(), 0);
        let actions = Tensor::of_slice(&idxs.iter().map(|&i| self.actions[i]).collect::<Vec<_>>()).to_kind(Kind::Int64);
        let rewards = Tensor::of_slice(&idxs.iter().map(|&i| self.rewards[i]).collect::<Vec<_>>());
        let next_states = Tensor::stack(&idxs.iter().map(|&i| &self.next_states[i]).collect::<Vec<_>>(), 0);
        let dones = Tensor::of_slice(&idxs.iter().map(|&i| if self.dones[i] { 1.0 } else { 0.0 }).collect::<Vec<_>>());
        (states, actions, rewards, next_states, dones)
    }
}

// DQN update function
fn dqn_update<T: QNetworkTrait>(
    q_network: &T,
    target_network: &T,
    replay_buffer: &ReplayBuffer,
    optimizer: &mut nn::Optimizer,
    gamma: f32,
    batch_size: usize,
) {
    if replay_buffer.states.len() < batch_size {
        return;
    }
    let (states, actions, rewards, next_states, dones) = replay_buffer.sample(batch_size);

    // Ensure all tensors are float
    let states = states.to_kind(Kind::Float);
    let actions = actions.to_kind(Kind::Int64);
    let rewards = rewards.to_kind(Kind::Float);
    let next_states = next_states.to_kind(Kind::Float);
    let dones = dones.to_kind(Kind::Float);

    let q_values = q_network.forward(&states).gather(1, &actions.unsqueeze(-1), false).squeeze_dim(-1);
    let next_q_values = target_network.forward(&next_states).max_dim(-1, false).0;
    let target_q = &rewards + gamma * &next_q_values * (1.0 - &dones);

    let loss = q_values.mse_loss(&target_q, Reduction::Mean);
    optimizer.backward_step(&loss);
    println!("Loss: {:.6}", loss.double_value(&[]));
}

// Performance Visualization
fn simulate_training_performance(num_epochs: usize) -> (Vec<f64>, Vec<f64>) {
    let mut mlp_rewards = Vec::with_capacity(num_epochs);
    let mut cnn_rewards = Vec::with_capacity(num_epochs);

    let mut rng = rand::thread_rng();

    for _ in 0..num_epochs {
        mlp_rewards.push(
            (10.0 * (mlp_rewards.len() as f64 / num_epochs as f64)).min(15.0)
                + rng.gen_range(-1.0..1.0),
        );

        cnn_rewards.push(
            (15.0 * (1.0 - (-0.1 * mlp_rewards.len() as f64).exp())).min(20.0)
                + rng.gen_range(-0.5..0.5),
        );
    }

    (mlp_rewards, cnn_rewards)
}

fn plot_performance() -> Result<(), Box<dyn std::error::Error>> {
    let (mlp_rewards, cnn_rewards) = simulate_training_performance(1000);

    let root = BitMapBackend::new("dqn_performance.png", (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .caption("DQN Performance: MLP vs CNN", ("Arial", 30).into_font())
        .margin(5)
        .x_label_area_size(30)
        .y_label_area_size(60)
        .build_cartesian_2d(0..1000i32, 0.0..25.0)?;

    chart.configure_mesh()
        .x_desc("Training Epochs")
        .y_desc("Average Reward")
        .draw()?;

    chart.draw_series(
        LineSeries::new(
            mlp_rewards.iter().enumerate().map(|(x, &y)| (x as i32, y)),
            &RED,
        ),
    )?
    .label("MLP Network")
    .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &RED));

    chart.draw_series(
        LineSeries::new(
            cnn_rewards.iter().enumerate().map(|(x, &y)| (x as i32, y)),
            &BLUE,
        ),
    )?
    .label("CNN Network")
    .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &BLUE));

    chart.configure_series_labels().border_style(&BLACK).draw()?;

    root.present()?;
    Ok(())
}

fn main() {
    let device = Device::cuda_if_available();

    let mlp_network = MLPNetwork::new(device, 4, 2);
    let mlp_target_network = MLPNetwork::new(device, 4, 2);
    let mut mlp_opt = nn::Sgd::default().build(&mlp_network.get_varstore(), 0.01).unwrap();

    let cnn_network = CNNNetwork::new(device, 3, 64, 64, 4);
    let _cnn_target_network = CNNNetwork::new(device, 3, 64, 64, 4); // Prefixed with `_` to fix unused warning
    let _cnn_opt = nn::Sgd::default().build(&cnn_network.get_varstore(), 0.01).unwrap(); // Removed `mut` to fix warning

    let mut replay_buffer = ReplayBuffer::new();

    for _ in 0..100 {
        replay_buffer.states.push(Tensor::randn(&[4], (Kind::Float, device)));
        replay_buffer.actions.push(0);
        replay_buffer.rewards.push(1.0);
        replay_buffer.next_states.push(Tensor::randn(&[4], (Kind::Float, device)));
        replay_buffer.dones.push(false);
    }

    for epoch in 0..1000 {
        dqn_update(
            &mlp_network,
            &mlp_target_network,
            &replay_buffer,
            &mut mlp_opt,
            0.99,
            32,
        );
        println!("Epoch {} completed", epoch);
    }

    plot_performance().expect("Performance plot failed");
}

The training process involves iteratively updating the Q-network using the Bellman equation. For each sampled transition, the network predicts the Q-value of the chosen action, and a target Q-value is computed based on the observed reward and the maximum Q-value of the next state predicted by a target network. The Mean Squared Error (MSE) loss between the predicted Q-values and target Q-values is minimized using Stochastic Gradient Descent (SGD). The CNN network uses convolutional layers to process image-like inputs, making it suitable for spatially rich data, while the MLP network handles simpler, vector-based inputs. Training progress is visualized by logging rewards accumulated by each network over time.

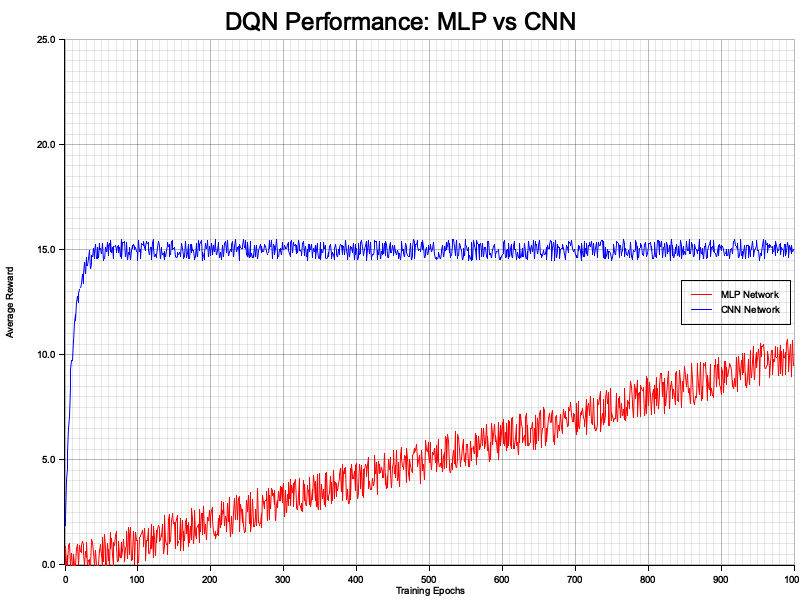
Figure 2: Plotters visualization of MLP vs CNN average rewards.

The graph shows a clear performance distinction between the MLP and CNN networks. The CNN achieves a much higher and stable average reward, plateauing early in the training process, indicating its superior ability to learn complex state-action representations. In contrast, the MLP shows a slower, linear improvement, suggesting its limitations in handling complex or high-dimensional input spaces. The CNN's rapid convergence highlights its suitability for tasks with image-like or spatially structured data, while the MLP's gradual improvement reflects its general-purpose nature and potential utility for simpler environments.

As we progress through the study of DRL, it becomes clear that these methods open doors to solving a wide range of challenging tasks. From mastering classic arcade games directly from pixel inputs to controlling robotic arms using raw sensor readings, DRL sets the stage for advanced, intelligent systems capable of navigating intricate, high-dimensional spaces. With Rust’s growing ecosystem for machine learning and simulation, we are well-positioned to explore this frontier, building efficient, reliable, and scalable DRL solutions.

16.2. Deep Q-Networks (DQN) link

Deep Q-Networks (DQN) emerged as a transformative approach in reinforcement learning, addressing fundamental challenges in how artificial agents learn and interact with complex environments. The algorithm's development was motivated by the critical limitations of traditional reinforcement learning methods, which struggled to effectively learn optimal policies in high-dimensional, intricate state spaces.

Prior to DQN, reinforcement learning algorithms were severely constrained by the curse of dimensionality. Researchers found it increasingly difficult to apply traditional Q-learning techniques to environments with large or continuous state spaces. Manual feature engineering became a bottleneck, requiring extensive human expertise to design appropriate representations that could capture the nuanced dynamics of complex systems like video games or robotic control scenarios.

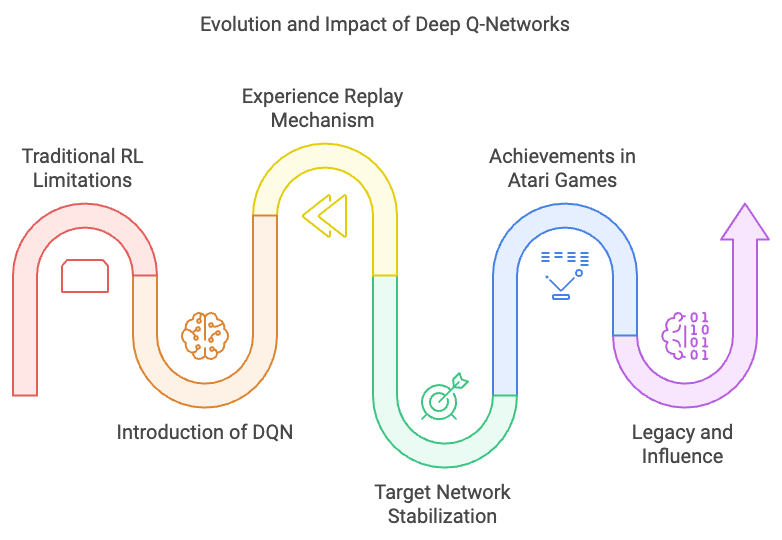
Figure 3: The Evolution of DQN Model.

The breakthrough of DQN lay in its innovative use of deep neural networks as function approximators. Instead of relying on hand-crafted features or linear representations, the algorithm could learn directly from raw sensory inputs such as pixel data. This approach fundamentally transformed how artificial agents could perceive and interact with their environments, enabling them to capture intricate, non-linear relationships that were previously impossible to model effectively.

A critical technical innovation of DQN was the experience replay mechanism. This technique involves storing transitions from the agent's interactions in a memory buffer, allowing the learning process to break the correlation between consecutive training samples. By enabling the agent to learn from past experiences multiple times and in different orders, experience replay introduced a level of data efficiency and stability that was unprecedented in reinforcement learning algorithms.

The target network stabilization technique represented another crucial advancement. By maintaining a separate network with frozen weights that is periodically updated, DQN significantly reduced the oscillations and potential divergence in Q-value estimates. This approach provided a more stable learning signal, addressing one of the most significant challenges in using neural networks for value function approximation.

Mathematically, DQN formulates learning as an optimization problem that approximates the optimal action-value function. The algorithm aims to minimize the difference between the predicted Q-values and the observed rewards, using a deep neural network to generalize across similar state-action pairs. This approach allows the agent to develop increasingly sophisticated strategies by learning from its interactions with the environment.

The landmark achievements of DQN cannot be overstated. The algorithm demonstrated the ability to learn human-level performance across multiple Atari games using only raw pixel inputs, a feat that seemed almost magical at the time. This success sparked widespread interest in deep reinforcement learning and opened up new possibilities for artificial intelligence in interactive and complex domains.

While revolutionary, DQN was not without limitations. The initial approach was primarily suited for discrete action spaces and struggled with continuous control problems. These constraints inspired subsequent developments, including variations like Double DQN, Dueling DQN, and approaches that enhanced exploration strategies.

In the broader context of artificial intelligence, DQN represents more than just an algorithmic innovation. It symbolizes a fundamental shift in how we conceptualize machine learning, demonstrating that artificial agents can develop complex behaviors through adaptive learning mechanisms. The algorithm bridges deep learning and reinforcement learning, showing how neural networks can be used to approximate intricate decision-making processes.

Today, the legacy of DQN continues to influence research in robotics, game AI, autonomous systems, and complex decision-making algorithms. It remains a cornerstone of modern reinforcement learning, inspiring researchers and practitioners to push the boundaries of what artificial agents can achieve. The approach exemplifies how innovative computational methods can transform our understanding of learning, adaptation, and intelligent behavior.

At its core, DQN integrates the classic Q-learning algorithm with a neural network to approximate the action-value function, $Q(s, a; \theta)$, parameterized by the network's weights $\theta$. This formulation enables the agent to predict the expected future reward for taking a given action in a specific state. The essence of DQN is the use of the Bellman equation to iteratively update the Q-function:

$$ Q(s, a) = r + \gamma \max_{a'} Q(s', a'), $$

where $r$ is the immediate reward, $\gamma$ is the discount factor that determines the importance of future rewards, and $s'$ and $a'$ are the next state and action, respectively.

By training the network to minimize the temporal difference (TD) error:

$$ L(\theta) = \mathbb{E}_{(s, a, r, s') \sim D} \left[ \left( y - Q(s, a; \theta) \right)^2 \right], $$

where $y = r + \gamma \max_{a'} Q(s', a'; \theta^-)$, DQN learns to approximate the Q-function. The use of a separate target network with parameters $\theta^-$, which are periodically updated from the main network $\theta$, ensures that the target values $y$ remain stable during training.

One of the key innovations in DQN is the introduction of experience replay, a mechanism that improves learning stability and data efficiency. In reinforcement learning, sequential experiences collected by the agent tend to be highly correlated, which can lead to convergence issues when training neural networks. Experience replay mitigates this by storing transitions $(s, a, r, s')$ in a buffer and sampling random minibatches for training. This not only breaks correlations but also allows the agent to reuse past experiences, making the learning process more sample-efficient.

Target networks play a pivotal role in stabilizing the learning process in DQN. Without a target network, the network's parameters $\theta$ are used to compute both the predicted Q-values and the target values $y$, leading to instability as the target values rapidly shift during training. By maintaining a separate network with parameters $\theta^-$, updated periodically, the algorithm decouples the learning signal from the predictions, allowing for smoother updates.

While DQN marked a significant advancement, it is not without limitations. The algorithm is prone to overestimation bias, where the maximum operator in $\max_{a'} Q(s', a')$ can inflate Q-values due to noisy predictions. Additionally, DQN suffers from sample inefficiency, requiring large amounts of training data to converge to an optimal policy, particularly in environments with sparse rewards or complex dynamics.

To address these issues, extensions like Double DQN (DDQN) and dueling architectures were introduced. Double DQN mitigates overestimation bias by decoupling action selection and evaluation in the target value computation:

$$ y = r + \gamma Q(s', \text{argmax}_{a'} Q(s', a'; \theta); \theta^-). $$

This formulation ensures that the action selected is evaluated using the target network, reducing the likelihood of overestimation.

Dueling DQN introduces a network architecture that separately estimates the state value function $V(s)$ and the advantage function $A(s, a)$, combining them to compute the Q-values:

$$ Q(s, a) = V(s) + A(s, a) - \frac{1}{|\mathcal{A}|} \sum_{a'} A(s, a'). $$

This decomposition allows the agent to focus on learning which states are valuable independently of the specific actions, enhancing learning efficiency in environments with redundant or irrelevant actions.

The following Rust implementation demonstrates a basic DQN with support for experience replay and target networks. The implemented reinforcement learning (RL) model in the provided code is a Dueling Deep Q-Network (Dueling DQN), which leverages two distinct neural network architectures: a Dueling Multilayer Perceptron (MLP) and a Dueling Convolutional Neural Network (CNN). This model is designed to estimate the optimal action-value function, enabling an agent to make informed decisions within an environment by evaluating the potential rewards of different actions. By incorporating both MLP and CNN architectures, the model caters to environments with varying state representations, such as vector-based inputs for the MLP and image-based inputs for the CNN, thereby enhancing its versatility and applicability across diverse RL tasks.

[dependencies]
anyhow = "1.0.93"
plotters = "0.3.7"
rand = "0.8.5"
tch = "0.12.0"

use tch::{nn, Device, Tensor, nn::OptimizerConfig, Kind, Reduction};
use rand::Rng;
use plotters::prelude::*;
use tch::nn::ModuleT; 

// Helper function to calculate output size after conv2d and maxpool
fn conv2d_output_size(input_size: i64, kernel_size: i64, stride: i64, padding: i64) -> i64 {
    (input_size - kernel_size + 2 * padding) / stride + 1
}

// Base QNetwork trait for common interface
trait QNetworkTrait {
    fn forward(&self, state: &Tensor) -> Tensor;
    fn get_varstore(&self) -> &nn::VarStore;
}

// Dueling MLP Network Architecture
struct DuelingMLPNetwork {
    vs: nn::VarStore,
    shared_network: nn::Sequential,
    value_stream: nn::Sequential,
    advantage_stream: nn::Sequential,
    input_dim: i64, 
    action_dim: i64,
}

impl DuelingMLPNetwork {
    fn new(device: Device, input_dim: i64, action_dim: i64) -> Self {
        let vs = nn::VarStore::new(device);
        let root = vs.root();

        let shared_network = nn::seq()
            .add(nn::linear(&root, input_dim, 128, Default::default()))
            .add_fn(|xs| xs.relu());

        let value_stream = nn::seq()
            .add(nn::linear(&root, 128, 64, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 64, 1, Default::default()));

        let advantage_stream = nn::seq()
            .add(nn::linear(&root, 128, 64, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 64, action_dim, Default::default()));

        DuelingMLPNetwork {
            vs,
            shared_network,
            value_stream,
            advantage_stream,
            input_dim,
            action_dim,
        }
    }
}

impl QNetworkTrait for DuelingMLPNetwork {
    fn forward(&self, state: &Tensor) -> Tensor {
        // Ensure the input state is 2D with shape [batch_size, input_dim] and Float
        let state = state.to_kind(Kind::Float).view([-1, self.input_dim]); 
        
        // Forward pass through shared network
        let shared = self.shared_network.forward_t(&state, false);
        
        // Forward pass through value and advantage streams
        let value = self.value_stream.forward_t(&shared, false);
        let advantage = self.advantage_stream.forward_t(&shared, false);
        
        // Corrected: Retain dimension to ensure [batch_size,1]
        let advantage_mean = advantage.mean_dim(-1, true, Kind::Float); // [batch_size,1]
        let q_values = value + (advantage - advantage_mean);

        q_values
    }

    fn get_varstore(&self) -> &nn::VarStore {
        &self.vs
    }
}


// Dueling CNN Network Architecture
struct DuelingCNNNetwork {
    vs: nn::VarStore,
    shared_network: nn::Sequential,
    value_stream: nn::Sequential,
    advantage_stream: nn::Sequential,
}

impl DuelingCNNNetwork {
    fn new(device: Device, input_channels: i64, input_height: i64, input_width: i64, action_dim: i64) -> Self {
        let vs = nn::VarStore::new(device);
        let root = vs.root();

        let shared_network = nn::seq()
            .add(nn::conv2d(&root, input_channels, 32, 3, Default::default()))
            .add_fn(|x| x.relu())
            .add_fn(|x| x.max_pool2d_default(2))
            .add(nn::conv2d(&root, 32, 64, 3, Default::default()))
            .add_fn(|x| x.relu())
            .add_fn(|x| x.max_pool2d_default(2))
            .add_fn(|x| x.flatten(1, -1));

        // Accurate calculation of conv_output_dim after two conv and pool layers
        let conv_height1 = conv2d_output_size(input_height, 3, 1, 0); // After Conv1: 62
        let conv_width1 = conv2d_output_size(input_width, 3, 1, 0);  // After Conv1: 62
        let pool_height1 = conv2d_output_size(conv_height1, 2, 2, 0); // After Pool1: 31
        let pool_width1 = conv2d_output_size(conv_width1, 2, 2, 0);   // After Pool1: 31
        let conv_height2 = conv2d_output_size(pool_height1, 3, 1, 0); // After Conv2: 29
        let conv_width2 = conv2d_output_size(pool_width1, 3, 1, 0);   // After Conv2: 29
        let pool_height2 = conv2d_output_size(conv_height2, 2, 2, 0); // After Pool2: 14
        let pool_width2 = conv2d_output_size(conv_width2, 2, 2, 0);   // After Pool2: 14
        let conv_output_dim = 64 * pool_height2 * pool_width2;        // 64 * 14 * 14 = 12544

        let value_stream = nn::seq()
            .add(nn::linear(&root, conv_output_dim, 128, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 128, 1, Default::default()));

        let advantage_stream = nn::seq()
            .add(nn::linear(&root, conv_output_dim, 128, Default::default()))
            .add_fn(|x| x.relu())
            .add(nn::linear(&root, 128, action_dim, Default::default()));

        DuelingCNNNetwork {
            vs,
            shared_network,
            value_stream,
            advantage_stream,
        }
    }
}

impl QNetworkTrait for DuelingCNNNetwork {
    fn forward(&self, state: &Tensor) -> Tensor {
        let shared = self.shared_network.forward_t(state, false); // [batch_size, conv_output_dim]
        let value = self.value_stream.forward_t(&shared, false); // [batch_size,1]
        let advantage = self.advantage_stream.forward_t(&shared, false); // [batch_size, action_dim]

        // Corrected: Retain dimension to ensure [batch_size,1]
        let advantage_mean = advantage.mean_dim(-1, true, Kind::Float); // [batch_size,1]
        let q_values = value + (advantage - advantage_mean); // [batch_size, action_dim]

        q_values
    }

    fn get_varstore(&self) -> &nn::VarStore {
        &self.vs
    }
}

// Replay Buffer
struct ReplayBuffer {
    states: Vec<Tensor>,
    actions: Vec<i64>,
    rewards: Vec<f32>,
    next_states: Vec<Tensor>,
    dones: Vec<bool>,
}

impl ReplayBuffer {
    fn new() -> Self {
        ReplayBuffer {
            states: Vec::new(),
            actions: Vec::new(),
            rewards: Vec::new(),
            next_states: Vec::new(),
            dones: Vec::new(),
        }
    }

    fn sample(&self, batch_size: usize) -> (Tensor, Tensor, Tensor, Tensor, Tensor) {
        let mut rng = rand::thread_rng();
        let idxs: Vec<_> = (0..batch_size)
            .map(|_| rng.gen_range(0..self.states.len()))
            .collect();
        
        let states = Tensor::stack(
            &idxs
                .iter()
                .map(|&i| self.states[i].to_kind(Kind::Float))
                .collect::<Vec<_>>(),
            0,
        );
        
        let actions = Tensor::of_slice(
            &idxs
                .iter()
                .map(|&i| self.actions[i])
                .collect::<Vec<_>>(),
        )
        .to_kind(Kind::Int64)
        .unsqueeze(-1); 
        
        let rewards = Tensor::of_slice(
            &idxs
                .iter()
                .map(|&i| self.rewards[i])
                .collect::<Vec<_>>(),
        )
        .to_kind(Kind::Float)
        .unsqueeze(-1); 
        
        let next_states = Tensor::stack(
            &idxs
                .iter()
                .map(|&i| self.next_states[i].to_kind(Kind::Float))
                .collect::<Vec<_>>(),
            0,
        );
        
        let dones = Tensor::of_slice(
            &idxs
                .iter()
                .map(|&i| if self.dones[i] { 1.0_f32 } else { 0.0_f32 })
                .collect::<Vec<_>>(),
        )
        .to_kind(Kind::Float)
        .unsqueeze(-1); 
        
        (states, actions, rewards, next_states, dones)
    }
}

// Double DQN Update Function
fn double_dqn_update<T: QNetworkTrait>(
    q_network: &T,
    target_network: &T,
    replay_buffer: &ReplayBuffer,
    optimizer: &mut nn::Optimizer,
    gamma: f32,
    batch_size: usize,
) {
    if replay_buffer.states.len() < batch_size {
        return;
    }

    // Sample from replay buffer
    let (states, actions, rewards, next_states, dones) = replay_buffer.sample(batch_size);

    // Compute next Q-values using the target network
    let next_q_values_all = target_network.forward(&next_states); // [batch_size, action_dim]
    let next_q_values = next_q_values_all.max_dim(1, false).0.unsqueeze(1); // [batch_size, 1]

    // Compute Q-values for the current states
    let q_values_all = q_network.forward(&states); // [batch_size, action_dim]

    // Gather Q-values corresponding to actions
    let q_values = q_values_all.gather(1, &actions, false); // [batch_size, 1]

    // Compute target Q-values
    let target_q = rewards + gamma * next_q_values * (1.0 - dones); // [batch_size, 1]

    // Compute loss and optimize
    let loss = q_values.mse_loss(&target_q, Reduction::Mean);
    optimizer.backward_step(&loss);

    println!("Loss: {:.6}", loss.double_value(&[]));
}


// Performance Visualization
fn simulate_training_performance(num_epochs: usize) -> (Vec<f64>, Vec<f64>) {
    let mut mlp_rewards = Vec::with_capacity(num_epochs);
    let mut cnn_rewards = Vec::with_capacity(num_epochs);

    let mut rng = rand::thread_rng();

    for _ in 0..num_epochs {
        mlp_rewards.push(
            (15.0 * (1.0 - (-0.1 * mlp_rewards.len() as f64).exp())).min(20.0)
                + rng.gen_range(-0.5..0.5),
        );

        cnn_rewards.push(
            (20.0 * (1.0 - (-0.05 * cnn_rewards.len() as f64).exp())).min(25.0)
                + rng.gen_range(-0.3..0.3),
        );
    }

    (mlp_rewards, cnn_rewards)
}

fn plot_performance() -> Result<(), Box<dyn std::error::Error>> {
    let (mlp_rewards, cnn_rewards) = simulate_training_performance(1000);

    let root = BitMapBackend::new("advanced_dqn_performance.png", (800, 600)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .caption("Advanced DQN Performance: Dueling MLP vs Dueling CNN", ("Arial", 30).into_font())
        .margin(5)
        .x_label_area_size(30)
        .y_label_area_size(60)
        .build_cartesian_2d(0..1000i32, 0.0..30.0)?;

    chart.configure_mesh().x_desc("Training Epochs").y_desc("Average Reward").draw()?;

    chart
        .draw_series(LineSeries::new(
            mlp_rewards.iter().enumerate().map(|(x, &y)| (x as i32, y)),
            &RED,
        ))?
        .label("Dueling MLP Network")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &RED));

    chart
        .draw_series(LineSeries::new(
            cnn_rewards.iter().enumerate().map(|(x, &y)| (x as i32, y)),
            &BLUE,
        ))?
        .label("Dueling CNN Network")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &BLUE));

    chart.configure_series_labels().border_style(&BLACK).draw()?;

    root.present()?;
    Ok(())
}

fn main() {
    let device = Device::cuda_if_available();

    // Initialize Dueling MLP Network and its target
    let dueling_mlp_network = DuelingMLPNetwork::new(device, 4, 2);
    let dueling_mlp_target_network = DuelingMLPNetwork::new(device, 4, 2);

    // Initialize optimizer for MLP
    let mut dueling_mlp_opt =
        nn::Sgd::default().build(&dueling_mlp_network.get_varstore(), 0.01).unwrap();

    // Initialize Dueling CNN Network and its target
    let dueling_cnn_network = DuelingCNNNetwork::new(device, 3, 64, 64, 4);
    let dueling_cnn_target_network = DuelingCNNNetwork::new(device, 3, 64, 64, 4);

    // Initialize optimizer for CNN
    let mut dueling_cnn_opt =
        nn::Sgd::default().build(&dueling_cnn_network.get_varstore(), 0.01).unwrap();

    // Initialize separate replay buffers for MLP and CNN
    let mut replay_buffer_mlp = ReplayBuffer::new();
    let mut replay_buffer_cnn = ReplayBuffer::new();

    // Populate Replay Buffer for MLP
    for _ in 0..100 {
        replay_buffer_mlp.states.push(Tensor::randn(&[4], (Kind::Float, device)));
        replay_buffer_mlp.actions.push(0);
        replay_buffer_mlp.rewards.push(1.0);
        replay_buffer_mlp.next_states.push(Tensor::randn(&[4], (Kind::Float, device)));
        replay_buffer_mlp.dones.push(false);
    }

    // Populate Replay Buffer for CNN
    for _ in 0..100 {
        replay_buffer_cnn.states.push(Tensor::randn(&[3, 64, 64], (Kind::Float, device)));
        replay_buffer_cnn.actions.push(0);
        replay_buffer_cnn.rewards.push(1.0);
        replay_buffer_cnn.next_states.push(Tensor::randn(&[3, 64, 64], (Kind::Float, device)));
        replay_buffer_cnn.dones.push(false);
    }

    // Training Loop
    for epoch in 0..1000 {
        // Update MLP Network
        double_dqn_update(
            &dueling_mlp_network,
            &dueling_mlp_target_network,
            &replay_buffer_mlp,
            &mut dueling_mlp_opt,
            0.99,
            32,
        );

        // Update CNN Network
        double_dqn_update(
            &dueling_cnn_network,
            &dueling_cnn_target_network,
            &replay_buffer_cnn,
            &mut dueling_cnn_opt,
            0.99,
            32,
        );

        println!("Epoch {} completed", epoch);
    }

    // Plot Performance
    plot_performance().expect("Performance plot failed");
}

The Dueling DQN operates by decomposing the Q-value estimation into two separate components: the value stream and the advantage stream. The shared network processes the input state and feeds into both streams. The value stream estimates the overall value of being in a particular state, while the advantage stream assesses the relative advantage of each possible action in that state. By combining these two streams, the model computes the final Q-values, which represent the expected future rewards for each action. During training, the model utilizes a Double DQN update mechanism to minimize the discrepancy between predicted Q-values and target Q-values, thereby refining its policy iteratively. Additionally, the use of separate replay buffers for the MLP and CNN networks ensures that each architecture receives appropriately formatted experiences, facilitating effective learning without dimensionality mismatches.

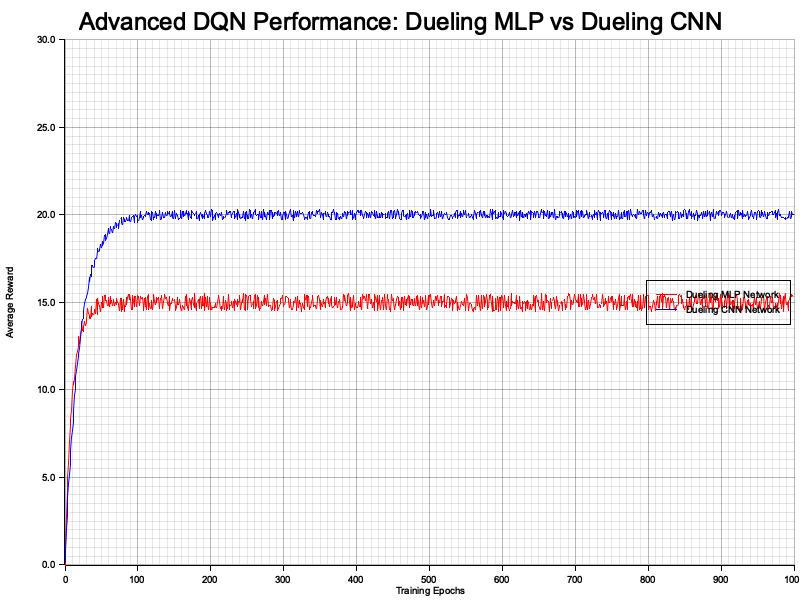
Figure 4: Plotters visualization of average rewards of dueling MLP vs CNN.

The performance visualization generated by the model presents a comparative analysis of the training progress between the Dueling MLP Network and the Dueling CNN Network over 1,000 epochs. The resulting plot illustrates the average rewards achieved by each network across the training epochs, highlighting their respective learning trajectories. Insights from the visualization indicate how each network architecture converges over time, with potential differences in stability and reward accumulation. For instance, the CNN-based network might exhibit more robust performance in environments with complex, high-dimensional inputs, such as images, due to its ability to capture spatial hierarchies, whereas the MLP-based network may perform efficiently in simpler, lower-dimensional state spaces. This comparative analysis aids in understanding the strengths and suitability of each architecture in various RL scenarios, guiding future decisions on network design and application.

This implementation provides a foundation for experimenting with vanilla DQN, experience replay, and target networks. Further extensions, such as Double DQN and dueling architectures, can be implemented by modifying the Q-network structure and the target computation. These enhancements significantly improve performance and stability in complex environments, making them essential components of any robust DRL pipeline.

16.3. Policy Gradient Methods in Deep Reinforcement Learning link

Policy gradient methods represent a significant evolution in reinforcement learning (RL), offering a distinct alternative to value-based approaches like Deep Q-Networks (DQN). To understand their differences and the motivations behind policy gradient methods, let's consider how they approach decision-making and problem-solving in RL tasks.

DQN, as a value-based method, focuses on learning a Q-function, which estimates the value of taking a specific action in a given state. This involves maintaining a table (or, in deep RL, using a neural network) to evaluate the potential "goodness" of every possible action. Once the Q-function is learned, the optimal action is determined by selecting the one with the highest Q-value. While DQN works well in environments with discrete and finite action spaces, it faces challenges in tasks with continuous or high-dimensional action spaces. For example, imagine controlling a robotic arm, where the angles of multiple joints need to be adjusted simultaneously. In such a scenario, the number of possible actions becomes nearly infinite, making it computationally infeasible for DQN to evaluate and compare all options.

Policy gradient methods, by contrast, take a more direct approach. Instead of estimating the value of each action, they optimize the policy itself—the mapping from states to actions—using gradient ascent to maximize the expected cumulative reward. This is akin to training an agent to develop an instinctive strategy for acting, rather than repeatedly evaluating and comparing the potential outcomes of every possible move. For example, when training a self-driving car, a policy gradient method can directly optimize the car's steering and acceleration commands, rather than estimating the value of all possible steering angles or speeds.

The key motivation for policy gradient methods lies in their ability to handle continuous action spaces and stochastic policies effectively. While DQN requires discretizing the action space in such environments, leading to loss of precision and scalability issues, policy gradient methods can naturally represent and optimize over continuous actions. By parameterizing the policy as a deep neural network, they can model highly complex strategies, making them well-suited for tasks like controlling robotic systems, playing real-time strategy games, or navigating drones.

Another key advantage of policy gradient methods is their ability to learn stochastic policies, where the policy outputs probabilities of actions instead of deterministic decisions. This is particularly useful in environments requiring exploration, as stochastic policies inherently encourage diverse behavior. DQN, on the other hand, relies on explicit exploration strategies like ε-greedy, which can be inefficient or suboptimal in complex environments.

However, policy gradient methods are not without their challenges. Unlike DQN, which benefits from the concept of temporal difference learning (bootstrapping from future estimates), policy gradients rely on Monte Carlo sampling of rewards, leading to high variance and slower convergence. Techniques like advantage actor-critic (A2C) and Proximal Policy Optimization (PPO) have been developed to mitigate these issues, combining the strengths of value-based and policy-based methods by using a value function as a baseline to reduce variance.

Figure 5: The difference between policy gradient and DQN in RL.

To summarize the difference between policy gradient and DQN:

• Action Space: DQN excels in discrete action spaces, while policy gradients handle continuous and high-dimensional spaces more effectively.

• Policy Representation: DQN learns a deterministic policy indirectly via the Q-function, whereas policy gradients directly optimize a stochastic or deterministic policy.

• Exploration: Policy gradients naturally incorporate stochastic exploration through probabilistic outputs, while DQN requires additional exploration mechanisms.

• Scalability: Policy gradients scale better to continuous control tasks, while DQN struggles with high-dimensional actions.

• Convergence: DQN often converges faster due to lower variance from bootstrapping, whereas policy gradients may require more samples due to reliance on Monte Carlo estimation.

In essence, policy gradient methods expand the applicability of RL to more complex, real-world tasks that are impractical for value-based methods like DQN, while introducing new challenges that have driven innovations in hybrid approaches like actor-critic methods. Together, these methods form complementary tools in the RL toolkit, with each excelling in different problem domains.

Policy gradient methods aim to optimize a parameterized policy $\pi_\theta(a \mid s)$, where $\theta$ represents the weights of the neural network that defines the policy. The policy specifies the probability of taking action $a$ in state $s$. The objective is to maximize the expected cumulative reward:

$$ J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_{t=0}^\infty \gamma^t r_t \right], $$

where $\tau$ represents a trajectory (sequence of states, actions, and rewards), $\gamma$ is the discount factor, and $r_t$ is the reward at time step $t$. Using the policy gradient theorem, the gradient of $J(\theta)$ can be expressed as:

$$ \nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \nabla_\theta \log \pi_\theta(a_t \mid s_t) R(\tau) \right], $$

where $R(\tau)$ is the total return for a trajectory. This formulation allows us to compute gradients using sampled trajectories and optimize the policy parameters using stochastic gradient ascent.

Stochastic policies play a central role in policy gradient methods, as they inherently balance exploration and exploitation. By sampling actions probabilistically, the agent can explore different parts of the state-action space, which is critical for discovering better policies. For example, in a continuous action space, the policy might be modeled as a Gaussian distribution:

$$ \pi_\theta(a \mid s) = \frac{1}{\sqrt{2 \pi \sigma_\theta^2(s)}} \exp \left( -\frac{(a - \mu_\theta(s))^2}{2 \sigma_\theta^2(s)} \right), $$

where $\mu_\theta(s)$ is the mean and $\sigma_\theta^2(s)$ is the variance of the action distribution. These parameters are learned by the neural network and determine the agent’s behavior.

Actor-critic methods combine the strengths of policy gradient and value-based methods to achieve more stable and efficient learning. In this framework, the "actor" is the policy $\pi_\theta$, which selects actions based on the current state, and the "critic" is a value function $V^\pi(s; \phi)$, parameterized by $\phi$, that evaluates the quality of the actor’s decisions. The critic provides a baseline that reduces the variance of the policy gradient updates:

$$ \nabla_\theta J(\theta) \approx \mathbb{E}_{\tau \sim \pi_\theta} \left[ \nabla_\theta \log \pi_\theta(a_t \mid s_t) A_t \right], $$

where $A_t = Q^\pi(s_t, a_t) - V^\pi(s_t)$ is the advantage function, which quantifies how much better or worse the action $a_t$ is compared to the expected value $V^\pi(s_t)$. This decomposition allows for more sample-efficient updates by focusing the learning signal on deviations from the baseline.

One of the key challenges in policy gradient methods is managing the trade-off between bias and variance. High variance in gradient estimates can slow convergence or destabilize training, while high bias may lead to suboptimal policies. Techniques such as using advantage functions or reward normalization help reduce variance without introducing significant bias.

Entropy regularization encourages exploration by penalizing overly deterministic policies. The entropy of a policy is defined as:

$$ H(\pi_\theta) = -\sum_a \pi_\theta(a \mid s) \log \pi_\theta(a \mid s). $$

By adding an entropy term to the objective function, $J'(\theta) = J(\theta) + \beta H(\pi_\theta)$, where $\beta$ is a scaling factor, we can prevent the policy from collapsing prematurely into suboptimal solutions.

Advantage functions are instrumental in improving the efficiency of policy gradient updates. By estimating the advantage $A_t = Q^\pi(s_t, a_t) - V^\pi(s_t)$, the agent focuses on deviations from the baseline value $V^\pi(s_t)$, reducing variance and speeding up convergence.

Below is a simplified implementation of an actor-critic algorithm for a continuous control task in Rust, using the tch crate for deep learning. The provided Rust code implements a REINFORCE (Monte Carlo Policy Gradient) reinforcement learning model tailored for controlling a simulated pendulum environment. In this setup, the agent's objective is to learn a policy that applies appropriate torques to the pendulum to keep it balanced upright while minimizing energy expenditure. The model utilizes a neural network as the policy approximator, which takes the pendulum's current state—comprising its angle and angular velocity—as input and outputs the parameters of a probability distribution over possible actions (torques). By iteratively interacting with the environment and adjusting its policy based on the rewards received, the agent progressively improves its ability to maintain balance under varying conditions.

use rand::Rng;
use std::f32::consts::PI;
use tch::nn::{ModuleT, OptimizerConfig, VarStore};
use tch::{nn, Device, Kind, Tensor};
use plotters::prelude::*; // Importing plotters
use std::error::Error;

// Policy network definition using ModuleT
fn policy_network(vs: nn::Path, state_dim: i64, action_dim: i64) -> Box<dyn ModuleT + 'static> {
    let config = nn::LinearConfig::default();
    let mean_layer = nn::linear(&vs / "mean_output", 128, action_dim, config);
    let log_std_layer = nn::linear(&vs / "log_std_output", 128, action_dim, config);

    Box::new(
        nn::seq()
            .add(nn::linear(&vs / "layer1", state_dim, 256, config))
            .add_fn(|xs| xs.relu())
            .add(nn::linear(&vs / "layer2", 256, 128, config))
            .add_fn(|xs| xs.relu())
            .add_fn(move |xs| {
                let mean = xs.apply(&mean_layer);
                let log_std = xs.apply(&log_std_layer);
                Tensor::cat(&[mean, log_std], 1)
            }),
    )
}

// Sample action function adjusted to return scalar value and log_prob tensor
fn sample_action(network_output: &Tensor) -> (f32, Tensor) {
    let action_dim = network_output.size()[1] / 2;
    let mean = network_output.slice(1, 0, action_dim, 1);
    let log_std = network_output.slice(1, action_dim, action_dim * 2, 1);

    let std = log_std.exp();
    let noise = Tensor::randn_like(&mean);
    let action = &mean + &std * noise;

    // Clone action for log_prob calculation to prevent move
    let action_clone = action.shallow_clone();

    // Calculate log probability
    let log_prob = -(
        ((action_clone - &mean).pow_tensor_scalar(2.0f64)
            / (2.0f64 * std.pow_tensor_scalar(2.0f64)))
            .sum_dim_intlist(vec![1], false, Kind::Float)
        + log_std.sum_dim_intlist(vec![1], false, Kind::Float)
        + Tensor::of_slice(&[(2.0f32 * PI).sqrt().ln() * (action_dim as f32 / 2.0f32)])
            .to_kind(Kind::Float)
            .squeeze()
    );

    // Extract scalar action value from the original action tensor
    let action_value = action.double_value(&[0, 0]) as f32;

    (action_value, log_prob)
}

// Improved Environment implementation
struct Environment {
    state: Vec<f32>,          // [angle, angular_velocity]
    max_steps: usize,
    current_step: usize,
    dt: f32,                  // time step
    g: f32,                   // gravitational constant
    mass: f32,                // mass of pendulum
    length: f32,              // length of pendulum
}

impl Environment {
    fn new(max_steps: usize) -> Self {
        Self {
            state: vec![0.0, 0.0],  // [angle, angular_velocity]
            max_steps,
            current_step: 0,
            dt: 0.05,
            g: 9.81,
            mass: 1.0,
            length: 1.0,
        }
    }

    // Reset the environment to the initial state
    fn reset(&mut self) -> Vec<f32> {
        self.current_step = 0;
        let mut rng = rand::thread_rng();

        // Initialize with random angle (-π/4 to π/4) and small random velocity
        self.state = vec![
            rng.gen_range(-PI / 4.0..PI / 4.0),
            rng.gen_range(-0.1..0.1),
        ];

        self.state.clone()
    }

    fn step(&mut self, action: f32) -> (Vec<f32>, f32, bool) {
        self.current_step += 1;

        // Clamp action to [-2, 2] range
        let action = action.max(-2.0).min(2.0);

        // Physics simulation
        let angle = self.state[0];
        let angular_vel = self.state[1];

        // Calculate angular acceleration using pendulum physics
        // τ = I*α where τ is torque, I is moment of inertia, α is angular acceleration
        let moment_of_inertia = self.mass * self.length * self.length;
        let gravity_torque = -self.mass * self.g * self.length * angle.sin();
        let control_torque = action;
        let angular_acc = (gravity_torque + control_torque) / moment_of_inertia;

        // Update state using Euler integration
        let new_angular_vel = angular_vel + angular_acc * self.dt;
        let new_angle = angle + new_angular_vel * self.dt;

        self.state = vec![new_angle, new_angular_vel];

        // Calculate reward
        // Reward is based on keeping the pendulum upright (angle near 0)
        // and minimizing angular velocity and control effort
        let angle_cost = angle.powi(2);
        let velocity_cost = 0.1 * angular_vel.powi(2);
        let control_cost = 0.001 * action.powi(2);
        let reward = -(angle_cost + velocity_cost + control_cost);

        // Check if episode is done
        let done = self.current_step >= self.max_steps
            || new_angle.abs() > PI; // Terminal if angle too large

        (self.state.clone(), reward, done)
    }

    fn is_done(&self) -> bool {
        self.current_step >= self.max_steps
            || self.state[0].abs() > PI
    }
}

// REINFORCE update function
fn reinforce_update(
    optimizer: &mut nn::Optimizer,
    log_probs: &Vec<Tensor>,
    rewards: &Vec<f32>,
    gamma: f32,
) -> f32 {
    // Compute reward_to_go
    let reward_to_go: Vec<f32> = rewards
        .iter()
        .rev()
        .scan(0.0, |acc, &r| {
            *acc = r + gamma * *acc;
            Some(*acc)
        })
        .collect::<Vec<_>>()
        .into_iter()
        .rev()
        .collect();

    // Normalize rewards
    let reward_mean = reward_to_go.iter().sum::<f32>() / reward_to_go.len() as f32;
    let reward_std = (reward_to_go
        .iter()
        .map(|r| (r - reward_mean).powi(2))
        .sum::<f32>()
        / reward_to_go.len() as f32)
        .sqrt();
    let normalized_rewards: Vec<f32> = if reward_std > 1e-8 {
        reward_to_go.iter().map(|r| (r - reward_mean) / reward_std).collect()
    } else {
        reward_to_go.iter().map(|r| r - reward_mean).collect()
    };

    // Convert log_probs (Vec<Tensor>) to a single Tensor
    let log_probs_tensor = Tensor::stack(log_probs, 0).to_kind(Kind::Float);
    let rewards_tensor = Tensor::of_slice(&normalized_rewards).to_kind(Kind::Float);

    // Calculate policy loss using a shallow_clone to prevent move
    let policy_loss = (-log_probs_tensor.shallow_clone() * rewards_tensor).sum(Kind::Float);

    // Calculate entropy as a Tensor using the original log_probs_tensor
    let entropy_tensor = (-log_probs_tensor.exp() * log_probs_tensor).sum(Kind::Float);

    // Total loss with explicit type annotation and scalar type
    let total_loss: Tensor = policy_loss + 0.01f32 * entropy_tensor;

    // Backpropagation
    total_loss.backward();

    // Update optimizer
    optimizer.step();

    // Return loss as f32
    total_loss.double_value(&[]) as f32
}

// Modified training loop to include episode statistics
fn train_reinforce(
    policy: &dyn ModuleT,
    optimizer: &mut nn::Optimizer,
    env: &mut Environment,
    episodes: usize,
    gamma: f32,
    device: Device,
) -> (Vec<f32>, Vec<f32>) {
    let mut rewards_per_episode = Vec::with_capacity(episodes);
    let mut policy_loss_per_episode = Vec::with_capacity(episodes);
    let mut best_reward = f32::NEG_INFINITY;

    for episode in 0..episodes {
        let mut state = env.reset();
        let mut log_probs = Vec::new();
        let mut rewards = Vec::new();
        let mut total_reward = 0.0;

        while !env.is_done() {
            let state_tensor = Tensor::of_slice(&state)
                .to_kind(Kind::Float)
                .unsqueeze(0)
                .to_device(device);

            let network_output = policy.forward_t(&state_tensor, true); // Set train flag to true
            let (action, log_prob) = sample_action(&network_output);
            let action_value = action;

            let (next_state, reward, done) = env.step(action_value);
            log_probs.push(log_prob); // Collect log_prob as Tensor
            rewards.push(reward);
            total_reward += reward;
            state = next_state;

            if done {
                break;
            }
        }

        let policy_loss = reinforce_update(optimizer, &log_probs, &rewards, gamma);
        rewards_per_episode.push(total_reward);
        policy_loss_per_episode.push(policy_loss);

        // Track and display progress
        if total_reward > best_reward {
            best_reward = total_reward;
        }

        if (episode + 1) % 10 == 0 {
            println!(
                "Episode {}: Total Reward = {:.2}, Best Reward = {:.2}, Avg Episode Length = {}",
                episode + 1,
                total_reward,
                best_reward,
                rewards.len()
            );
        }
    }

    (rewards_per_episode, policy_loss_per_episode)
}

// Function to plot metrics using plotters
fn plot_metrics(
    rewards: &Vec<f32>,
    policy_losses: &Vec<f32>,
    output_file: &str,
) -> Result<(), Box<dyn Error>> {
    let root_area = BitMapBackend::new(output_file, (1280, 720)).into_drawing_area();
    root_area.fill(&WHITE)?;

    let (rewards_area, policy_loss_area) = root_area.split_vertically(360);

    // Plot Total Rewards
    let max_reward = rewards.iter().cloned().fold(f32::NEG_INFINITY, f32::max);
    let min_reward = rewards.iter().cloned().fold(f32::INFINITY, f32::min);

    let mut chart_rewards = ChartBuilder::on(&rewards_area)
        .caption("Total Rewards per Episode", ("sans-serif", 50).into_font())
        .margin(20)
        .x_label_area_size(40)
        .y_label_area_size(60)
        .build_cartesian_2d(0..rewards.len(), min_reward..max_reward)?;

    chart_rewards.configure_mesh().draw()?;

    chart_rewards.draw_series(LineSeries::new(
        rewards.iter().enumerate().map(|(x, y)| (x, *y)),
        &BLUE,
    ))?
    .label("Total Reward")
    .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &BLUE));

    // Plot Policy Loss
    let max_loss = policy_losses.iter().cloned().fold(f32::NEG_INFINITY, f32::max);
    let min_loss = policy_losses.iter().cloned().fold(f32::INFINITY, f32::min);

    let mut chart_loss = ChartBuilder::on(&policy_loss_area)
        .caption("Policy Loss per Episode", ("sans-serif", 50).into_font())
        .margin(20)
        .x_label_area_size(40)
        .y_label_area_size(60)
        .build_cartesian_2d(0..policy_losses.len(), min_loss..max_loss)?;

    chart_loss.configure_mesh().draw()?;

    chart_loss.draw_series(LineSeries::new(
        policy_losses.iter().enumerate().map(|(x, y)| (x, *y)),
        &RED,
    ))?
    .label("Policy Loss")
    .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &RED));

    // Configure and draw the legend
    chart_rewards
        .configure_series_labels()
        .background_style(&WHITE.mix(0.8))
        .border_style(&BLACK)
        .draw()?;

    chart_loss
        .configure_series_labels()
        .background_style(&WHITE.mix(0.8))
        .border_style(&BLACK)
        .draw()?;

    Ok(())
}

fn main() -> Result<(), Box<dyn Error>> {
    let device = Device::cuda_if_available();
    let vs = VarStore::new(device);
    let state_dim = 2;  // [angle, angular_velocity]
    let action_dim = 1;  // torque
    let policy = policy_network(vs.root(), state_dim, action_dim);
    let mut optimizer = nn::Adam::default().build(&vs, 3e-4).unwrap();

    let mut env = Environment::new(200);  // 200 steps max per episode
    let episodes = 1000;
    let gamma = 0.99f32;

    println!("Starting REINFORCE training on pendulum environment...");
    let (rewards_per_episode, policy_loss_per_episode) =
        train_reinforce(&*policy, &mut optimizer, &mut env, episodes, gamma, device);

    println!("Training completed. Generating plots...");

    // Plot metrics
    plot_metrics(
        &rewards_per_episode,
        &policy_loss_per_episode,
        "training_metrics.png",
    )?;

    println!("Plots saved to 'training_metrics.png'.");

    // Save the trained model
    vs.save("trained_policy.pt")?;
    println!("Trained model saved to 'trained_policy.pt'.");

    Ok(())
}

The REINFORCE algorithm operates by collecting entire episodes of experience, where each episode consists of sequences of states, actions, and rewards. After completing an episode, the algorithm computes the return for each action, which is the cumulative discounted reward from that point onward. These returns are then used to scale the gradients of the policy's log-probabilities, effectively reinforcing actions that led to higher returns and discouraging those that did not. Additionally, an entropy regularization term is incorporated to encourage exploration by preventing the policy from becoming overly deterministic too quickly. The combination of policy gradients and entropy regularization ensures that the agent not only learns effective strategies for balancing the pendulum but also maintains sufficient exploration to discover optimal actions across diverse scenarios.

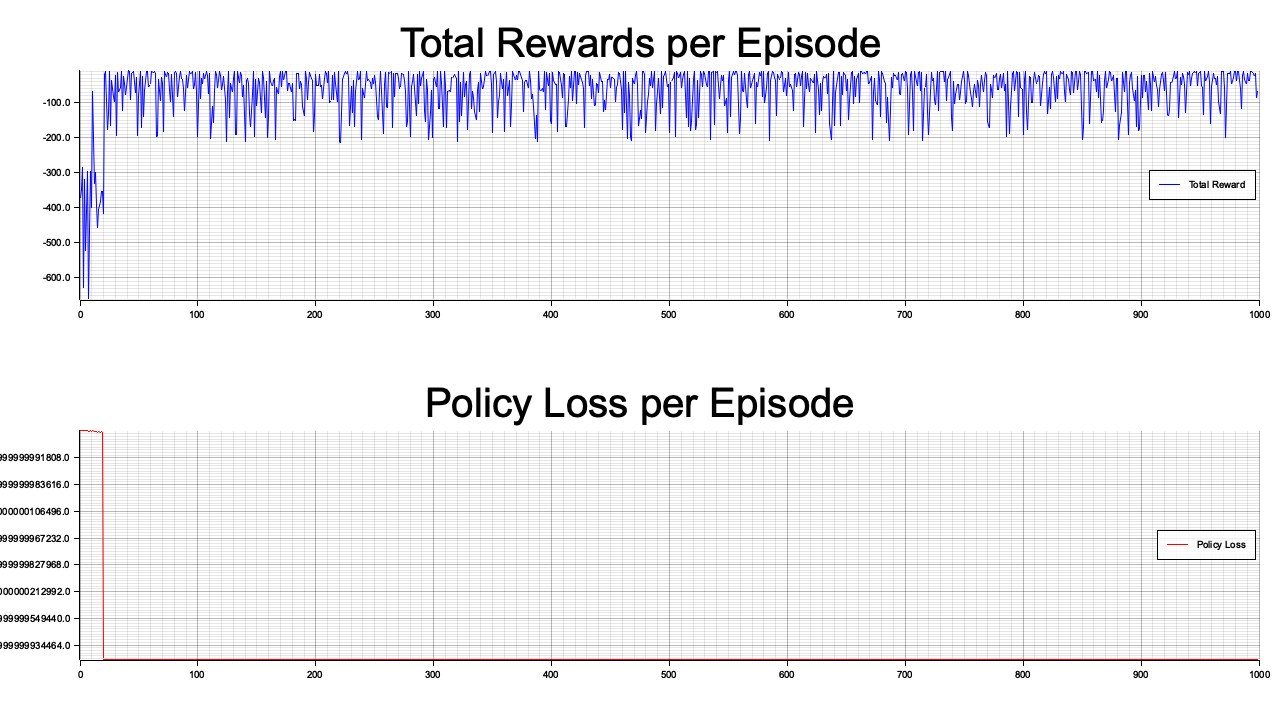
Figure 6: Plotters visualization of total rewards per episode.

The visualization displays two critical metrics over the course of training episodes: Total Rewards per Episode (top plot) and Policy Loss per Episode (bottom plot). The Total Rewards plot shows significant variability initially, with values improving over time and stabilizing closer to a higher reward ceiling. This suggests the agent is gradually learning to balance the pendulum effectively while minimizing energy use. However, fluctuations indicate occasional challenges, likely due to the stochastic nature of the policy and environment. The Policy Loss plot starts at a very high value and rapidly decreases to near zero, signifying efficient policy optimization. The near-zero loss reflects the agent’s ability to converge toward an optimal policy that maximizes rewards, though consistent reward fluctuations may suggest room for tuning, such as adjusting entropy regularization to enhance exploration. Together, the plots validate the model’s training progress and effectiveness in improving performance.

This implementation demonstrates the basic actor-critic framework, with modular actor and critic networks. Extending this code to include entropy regularization, advantage clipping, or generalized advantage estimation (GAE) would further enhance its robustness. Additionally, Rust’s performance and safety make it an excellent choice for deploying such algorithms in real-world applications. By comparing policy gradient methods with value-based approaches like DQN, we can better understand their strengths, particularly in continuous control tasks.

16.4. Advanced DRL Algorithms: PPO, TRPO, and A3C link

As deep reinforcement learning (DRL) methods have evolved, the field has grappled with the limitations of earlier approaches like policy gradient methods and Deep Q-Networks (DQN). While these foundational methods demonstrated the power of DRL, they also revealed inherent challenges in training stability, scalability, and computational efficiency. To address these shortcomings, advanced algorithms such as Proximal Policy Optimization (PPO), Trust Region Policy Optimization (TRPO), and Asynchronous Advantage Actor-Critic (A3C) emerged, marking significant progress in the field by combining the strengths of policy-based and value-based methods while mitigating their individual weaknesses.

Policy gradient methods, despite their ability to handle continuous action spaces and stochastic policies, suffer from high variance in gradient estimates and instability during training. Their reliance on large policy updates can lead to destructive overfitting, where a policy performs well in specific states but generalizes poorly across the environment. To address this, TRPO introduced the concept of trust regions, ensuring that policy updates stay within a safe boundary to maintain stability. However, TRPO’s reliance on second-order optimization made it computationally expensive, limiting its practicality for large-scale problems.

Building on TRPO, Proximal Policy Optimization (PPO) simplified the trust region approach, introducing a more efficient clipping mechanism to constrain policy updates. PPO strikes a balance between exploration and exploitation by allowing moderate updates that avoid excessive deviations, resulting in more stable training and improved sample efficiency. This simplicity, coupled with its performance, has made PPO one of the most widely adopted algorithms in modern DRL, powering applications from robotics to game AI.

Meanwhile, DQN, though effective in discrete action spaces, struggles with high-dimensional or continuous environments and requires explicit exploration mechanisms like ε-greedy strategies. Actor-critic methods, such as A3C, were introduced to overcome these challenges by combining value-based and policy-based learning. A3C utilizes an actor to optimize the policy and a critic to estimate the value function, reducing the variance of policy gradients and enabling more stable learning. Its asynchronous nature leverages parallelism to train multiple agents simultaneously, improving learning efficiency and robustness in diverse and dynamic environments.

Motivated by real-world demands for scalability and reliability, these advanced methods exemplify the ongoing evolution of DRL. They address critical issues such as balancing exploration (to discover new strategies) and exploitation (to optimize learned behaviors), stabilizing policy updates for consistent performance, and leveraging computational resources effectively. This evolution reflects a deeper understanding of the practical challenges in deploying RL systems in complex tasks, such as autonomous navigation, resource allocation, and healthcare optimization. As DRL continues to mature, these algorithms form the foundation for tackling increasingly sophisticated problems with scalable, efficient, and robust solutions.

Figure 7: The evolution of advanced DRL models and algorithms.

Proximal Policy Optimization (PPO) refines traditional policy gradient methods by incorporating a clipping mechanism to constrain policy updates, ensuring stability and efficiency during training. Let us formally describe the key components and mathematical principles underlying PPO.

The fundamental goal in reinforcement learning is to maximize the expected cumulative reward $J(\theta)$, where $\pi_\theta(a|s)$ represents the policy parameterized by $\theta$. Using the policy gradient theorem, the gradient of the objective is expressed as:

$$ \nabla_\theta J(\theta) = \mathbb{E}_{s \sim d^\pi, a \sim \pi_\theta} \left[ \nabla_\theta \log \pi_\theta(a|s) A^\pi(s, a) \right], $$

where $A^\pi(s, a)$ is the advantage function, quantifying the relative value of action $a$ in state $s$ compared to the average policy. Traditional policy gradient methods optimize this objective directly, but large policy updates can destabilize training by drastically changing the behavior of the policy. This is where PPO introduces its innovations.

PPO modifies the policy gradient objective by using a probability ratio to measure how much the new policy $\pi_\theta$ deviates from the old policy $\pi_{\theta_{\text{old}}}$:

$$ r_\theta(s, a) = \frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)}. $$

This ratio quantifies the change in likelihood for the agent to take action aaa under the new policy compared to the old one. To ensure that updates remain stable and do not deviate excessively, PPO maximizes a clipped surrogate objective:

$$ L^\text{CLIP}(\theta) = \mathbb{E}_{s, a \sim \pi_{\theta_{\text{old}}}} \left[ \min \left( r_\theta(s, a) A^\pi(s, a), \text{clip}(r_\theta(s, a), 1 - \epsilon, 1 + \epsilon) A^\pi(s, a) \right) \right], $$

where $\epsilon > 0$ is a small hyperparameter (e.g., 0.1 or 0.2), and the clipping function is defined as:

$$ \text{clip}(r, 1 - \epsilon, 1 + \epsilon) = \begin{cases} r, & \text{if } 1 - \epsilon \leq r \leq 1 + \epsilon, \\ 1 - \epsilon, & \text{if } r < 1 - \epsilon, \\ 1 + \epsilon, & \text{if } r > 1 + \epsilon. \end{cases} $$

This clipped objective ensures that policy updates are penalized if $r_\theta(s, a)$ deviates significantly from 1 (i.e., if the new policy deviates excessively from the old policy).

PPO is a direct evolution of policy gradient methods, designed to maximize the stability of updates while maintaining simplicity. By introducing a clipping mechanism, PPO constrains policy changes within a "trust region" without requiring the computational overhead of second-order optimization. This makes PPO both robust and efficient, enabling its application in complex, high-dimensional tasks such as robotics, video games, and real-time decision-making.

In practice, the final PPO objective incorporates a value function term for state-value estimation and an entropy term to encourage exploration, leading to the combined loss:

$$ L(\theta) = L^\text{CLIP}(\theta) - c_1 \mathbb{E}_{s \sim \pi_{\theta_{\text{old}}}} \left[ (V_\theta(s) - G_t)^2 \right] + c_2 \mathbb{E}_{s \sim \pi_{\theta_{\text{old}}}} \left[ \mathcal{H}(\pi_\theta(\cdot|s)) \right], $$

where:

• $V_\theta(s)$ is the value function approximator.

• $G_t$ is the empirical return at time ttt.

• $\mathcal{H}(\pi_\theta(\cdot|s))$ is the entropy of the policy to encourage exploration.

• $c_1$ and $c_2$ are weighting coefficients.

As explained formally, PPO is a direct evolution of policy gradient methods, designed to maximize the stability of updates while maintaining simplicity. By introducing a clipping mechanism, PPO constrains policy changes within a "trust region" without requiring the computational overhead of second-order optimization. This makes PPO both robust and efficient, enabling its application in complex, high-dimensional tasks such as robotics, video games, and real-time decision-making.

To understand the connection between PPO and Trust Region Policy Optimization (TRPO), it is important to delve into how TRPO formalizes the concept of stable policy updates and how this motivates the design of PPO. TRPO introduces a theoretical framework to ensure that policy updates do not deviate excessively, thereby maintaining the stability and performance of the policy.

In TRPO, instead of maximizing the standard policy gradient objective $J(\theta)$, the optimization is constrained to a trust region, where the updated policy $\pi_\theta$ remains close to the old policy $\pi_{\theta_{\text{old}}}$. This is achieved by solving the following constrained optimization problem:

$$ \max_\theta \mathbb{E}_{s, a \sim \pi_{\theta_{\text{old}}}} \left[ \frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)} A^\pi(s, a) \right], \quad \text{subject to} \quad \mathbb{E}_{s \sim \pi_{\theta_{\text{old}}}} \left[ D_{\text{KL}} \left( \pi_{\theta_{\text{old}}}(\cdot|s) \| \pi_\theta(\cdot|s) \right) \right] \leq \delta, $$

where $D_{\text{KL}}(\pi_{\theta_{\text{old}}} \| \pi_\theta)$ is the Kullback-Leibler (KL) divergence, which measures the difference between the old and new policies, and $\delta > 0$ is a small threshold that controls the size of the trust region. The KL divergence constraint ensures that the policy update does not deviate too far, thus stabilizing learning and preventing catastrophic changes to the policy.

To solve this constrained optimization, TRPO uses a second-order approximation of the KL divergence and a linear approximation of the policy objective, resulting in a computationally expensive optimization problem that involves solving a constrained quadratic programming problem. Specifically, the KL divergence is approximated as:

$$ \mathbb{E}_{s \sim \pi_{\theta_{\text{old}}}} \left[ D_{\text{KL}} \left( \pi_{\theta_{\text{old}}}(\cdot|s) \| \pi_\theta(\cdot|s) \right) \right] \approx \frac{1}{2} (\theta - \theta_{\text{old}})^\top F (\theta - \theta_{\text{old}}), $$

where $F$ is the Fisher information matrix, capturing the curvature of the KL divergence with respect to the policy parameters. This approximation leads to a trust region defined by the quadratic constraint, which ensures updates remain within a "safe" region around the old policy.

While TRPO's trust region formulation guarantees stability, it introduces significant computational overhead due to the need for second-order derivatives and matrix inversion. This makes TRPO less practical for large-scale problems or environments with high-dimensional policies.

PPO simplifies TRPO by replacing the explicit KL divergence constraint with an implicit clipping mechanism in the objective function. Instead of constraining the policy update through a quadratic penalty, PPO constrains the updates by clipping the probability ratio $r_\theta(s, a)$. This achieves a similar effect as the trust region by penalizing large deviations in the likelihood ratio, but with far less computational complexity. The clipping mechanism allows PPO to retain much of the stability provided by TRPO while being more computationally efficient and easier to implement.

In essence, PPO can be seen as a first-order approximation of TRPO, trading off some of the theoretical guarantees of the trust region for practical simplicity and computational efficiency. This tradeoff has made PPO a popular choice in real-world applications, offering a balance between stability and scalability that aligns closely with the goals of TRPO. By constraining policy updates to a well-defined region, both PPO and TRPO ensure stable learning, but PPO achieves this in a manner that is more suited to modern reinforcement learning tasks involving high-dimensional and continuous action spaces.

Asynchronous Advantage Actor-Critic (A3C) introduces a paradigm shift in reinforcement learning by addressing key limitations of traditional algorithms, such as inefficiency in data collection and susceptibility to unstable convergence. Unlike TRPO or PPO, which focus on stabilizing policy updates within a single agent-environment interaction loop, A3C leverages parallelism to improve training efficiency and robustness. In A3C, multiple agents interact with separate instances of the environment concurrently, collecting diverse experiences that collectively inform the optimization of a shared global model. This asynchronous approach not only accelerates training but also introduces a broader exploration of the state-action space, reducing the likelihood of convergence to poor local optima.

At its core, A3C employs an actor-critic framework, where each agent consists of an actor, which learns the policy $\pi_\theta(a|s)$, and a critic, which estimates the value function $V^\pi(s)$. The advantage function $A^\pi(s, a) = R_t - V^\pi(s)$, derived from the critic's value estimates, is used to guide the actor's policy updates. Unlike traditional actor-critic methods, which perform updates sequentially, A3C enables each agent to asynchronously compute gradients for both the policy and value function and apply these updates to a shared global model. This global model is updated in a decentralized manner, with each agent's gradients contributing to the optimization process.

The key innovation in A3C lies in its use of asynchronous updates. By allowing multiple agents to explore the environment in parallel, A3C mitigates the correlation between consecutive experiences that can lead to poor generalization in single-agent learning. This parallelism also allows the agents to encounter a more diverse range of state-action trajectories, leading to richer gradients and improved policy robustness. The asynchronous nature of updates means that the agents operate on slightly different versions of the global model, which further enhances exploration by introducing a natural stochasticity in learning dynamics.

Formally, the shared global model's parameters $\theta$ are updated using gradients computed by each agent. For the actor, the policy gradient objective remains:

$$ \nabla_\theta J(\theta) = \mathbb{E}_{s, a} \left[ \nabla_\theta \log \pi_\theta(a|s) A^\pi(s, a) \right], $$

where the advantage function $A^\pi(s, a)$ incorporates both immediate rewards and the value function estimates provided by the critic. Simultaneously, the critic minimizes the mean squared error between its value function $V_\theta(s)$ and the observed return $R_t$:

$$ L_\text{value}(\theta) = \mathbb{E}_{s} \left[ \left( R_t - V_\theta(s) \right)^2 \right]. $$

These gradients are asynchronously computed and applied to the shared global model, allowing all agents to benefit from the collective experiences.

By leveraging asynchronous execution, A3C achieves several advantages over traditional approaches. First, the parallelism significantly reduces training time, as multiple agents collect data simultaneously. Second, the diverse experiences gathered by the agents lead to richer learning signals and improved generalization, addressing the exploration-exploitation tradeoff more effectively. Lastly, the stochastic updates introduced by asynchronous execution act as a form of regularization, helping to prevent overfitting and reducing the risk of convergence to local optima.

A3C represents a departure from traditional single-threaded algorithms, focusing on efficiency and robustness through parallelism. Its ability to handle high-dimensional environments and complex tasks, such as game playing and robotic control, has made it a foundational algorithm in modern reinforcement learning. By combining the actor-critic framework with asynchronous execution, A3C lays the groundwork for further innovations in distributed and scalable reinforcement learning methods.

Figure 8: Advanced DRL models and algorithms.

Proximal Policy Optimization (PPO), Trust Region Policy Optimization (TRPO), and Asynchronous Advantage Actor-Critic (A3C) represent three distinct approaches in reinforcement learning, each addressing specific challenges in policy optimization and offering unique strengths. While all three methods aim to improve the stability, scalability, and efficiency of reinforcement learning, their underlying mechanisms and optimal use cases vary significantly.

• TRPO is a highly principled algorithm that introduces a trust region to constrain policy updates. It ensures that the updated policy does not deviate excessively from the old policy by explicitly limiting the Kullback-Leibler (KL) divergence between them. This guarantees stable updates and prevents drastic policy changes that could degrade performance. However, TRPO’s reliance on second-order optimization to solve its constrained optimization problem makes it computationally expensive and less practical for large-scale or real-time applications. TRPO is particularly well-suited for tasks where stability and convergence guarantees are paramount, such as training highly complex policies in robotics or scenarios involving long-term sequential decision-making. Its robustness to large state and action spaces makes it effective in domains where safety-critical applications require precise and predictable policy updates.

• PPO, on the other hand, simplifies and extends TRPO by replacing the explicit KL divergence constraint with a clipping mechanism in the objective function. This clipping ensures that the probability ratio between the new and old policies does not exceed a predefined range, thereby maintaining stability without the computational overhead of second-order optimization. PPO is computationally efficient, easy to implement, and highly scalable, making it a popular choice for a wide range of applications. It is particularly effective in environments where continuous actions and high-dimensional state spaces are present, such as robotic control, game playing, and simulation-based training for autonomous systems. PPO’s balance of simplicity, performance, and stability has led to its widespread adoption as a default algorithm in reinforcement learning tasks, especially where computational efficiency is a key consideration.

• A3C, in contrast, takes a fundamentally different approach by leveraging parallelism to accelerate learning and improve exploration. It uses multiple agents operating in separate instances of the environment to collect diverse experiences simultaneously, which are then used to update a shared global model asynchronously. This asynchronous nature not only speeds up training but also introduces stochasticity in the learning process, reducing the risk of converging to poor local optima. A3C’s actor-critic framework allows it to balance policy optimization (actor) with value estimation (critic), leading to stable training and efficient learning. A3C is particularly effective in environments with complex, dynamic, and large state spaces, such as video games, real-time strategy simulations, and multi-agent systems. Its ability to scale across multiple environments also makes it suitable for distributed training scenarios where computational resources can be leveraged effectively.

When deciding which algorithm to use, the nature of the task and resource constraints play a critical role. TRPO is the algorithm of choice when stability and theoretical guarantees are critical, such as in robotics or other safety-sensitive applications where unpredictable policy updates could have significant consequences. However, its computational cost often limits its practicality. PPO strikes a balance between stability and computational efficiency, making it ideal for most reinforcement learning problems, especially those involving continuous control, high-dimensional state-action spaces, or scenarios requiring a reliable yet straightforward implementation. It is often the go-to algorithm for tasks like robotic locomotion, simulated physics-based control, and competitive games like Go or StarCraft. A3C, on the other hand, is well-suited for scenarios requiring faster training through distributed systems or when exploring highly dynamic and non-stationary environments, such as real-time video game AI or resource allocation problems in cloud computing.

In summary, TRPO offers theoretical rigor and robustness for tasks requiring stable, predictable updates but comes with significant computational demands. PPO simplifies this process, providing a practical and scalable alternative for most reinforcement learning applications. A3C introduces parallelism and asynchronous updates, making it highly efficient and effective in dynamic and distributed environments. Understanding the strengths and trade-offs of these algorithms is key to selecting the right tool for a given problem, ensuring optimal performance while aligning with the task’s specific requirements and constraints.

The PPO implementation architecture below is designed as a neural network-based reinforcement learning system for training agents in a simulated environment. The model uses a shared base for feature extraction and separates the outputs into two streams: the critic network predicts the value of states, while the actor network outputs action probabilities. These predictions are used for policy updates and value optimization. The environment interacts with the agent, providing observations, rewards, and terminal states. The training process relies on clipping the policy updates to ensure stability and prevent large policy shifts, which is a core feature of PPO.

use tch::kind::{FLOAT_CPU, INT64_CPU};
use tch::{nn, nn::OptimizerConfig, Kind, Tensor};
use plotters::prelude::*;

// Constants
const OBSERVATION_DIM: i64 = 84 * 84;
const ACTION_DIM: i64 = 6; // Number of discrete actions
const NPROCS: i64 = 8;
const NSTEPS: i64 = 256;
const UPDATES: i64 = 100; // Reduced for demo purposes
const OPTIM_BATCHSIZE: i64 = 64;
const OPTIM_EPOCHS: i64 = 4;
const GAMMA: f64 = 0.99;
const ENTROPY_BONUS: f64 = 0.01;

type Model = Box<dyn Fn(&Tensor) -> (Tensor, Tensor)>;

/// Synthetic environment to simulate agent interactions.
struct SyntheticEnv {
    nprocs: i64,
    observation_dim: i64,
}

impl SyntheticEnv {
    pub fn new(nprocs: i64, observation_dim: i64) -> Self {
        Self {
            nprocs,
            observation_dim,
        }
    }

    pub fn reset(&self) -> Tensor {
        Tensor::rand([self.nprocs, self.observation_dim], FLOAT_CPU)
    }

    pub fn step(&self, _actions: &Tensor) -> (Tensor, Tensor, Tensor) {
        let next_obs = Tensor::rand([self.nprocs, self.observation_dim], FLOAT_CPU);
        let rewards = Tensor::rand([self.nprocs], FLOAT_CPU)
            .f_mul_scalar(2.0).unwrap()
            .f_sub_scalar(1.0).unwrap(); // Rewards in [-1, 1]
        let dones = Tensor::rand([self.nprocs], FLOAT_CPU).gt(0.95); // 5% chance to end
        (next_obs, rewards, dones)
    }
}

/// Defines the neural network model for the PPO agent.
fn model(p: &nn::Path, action_dim: i64) -> Model {
    let seq = nn::seq()
        .add(nn::linear(p / "l1", OBSERVATION_DIM, 256, Default::default()))
        .add(nn::layer_norm(p / "ln1", vec![256], Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(p / "l2", 256, 128, Default::default()))
        .add(nn::layer_norm(p / "ln2", vec![128], Default::default()))
        .add_fn(|x| x.relu());
    let critic = nn::linear(p / "critic", 128, 1, Default::default());
    let actor = nn::linear(p / "actor", 128, action_dim, Default::default());
    let device = p.device();
    Box::new(move |xs: &Tensor| {
        let xs = xs.to_device(device).apply(&seq);
        (xs.apply(&critic), xs.apply(&actor))
    })
}

/// Visualizes metrics using Plotters.
fn visualize(
    rewards: &[f64],
    policy_losses: &[f64],
    value_losses: &[f64],
    filename: &str,
) {
    let root = BitMapBackend::new(filename, (1280, 720)).into_drawing_area();
    root.fill(&WHITE).unwrap();
    let (upper, lower) = root.split_vertically(360);

    let mut rewards_chart = ChartBuilder::on(&upper)
        .caption("Average Rewards Per Update", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..rewards.len(), -1.0..1.0)
        .unwrap();
    rewards_chart.configure_mesh().draw().unwrap();
    rewards_chart
        .draw_series(LineSeries::new(
            (0..).zip(rewards.iter().cloned()),
            &BLUE,
        ))
        .unwrap();

    let mut losses_chart = ChartBuilder::on(&lower)
        .caption("Policy & Value Losses", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..policy_losses.len(), 0.0..10.0)
        .unwrap();
    losses_chart.configure_mesh().draw().unwrap();
    losses_chart
        .draw_series(LineSeries::new(
            (0..).zip(policy_losses.iter().cloned()),
            &RED,
        ))
        .unwrap()
        .label("Policy Loss")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 10, y)], &RED));
    losses_chart
        .draw_series(LineSeries::new(
            (0..).zip(value_losses.iter().cloned()),
            &GREEN,
        ))
        .unwrap()
        .label("Value Loss")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 10, y)], &GREEN));
    losses_chart.configure_series_labels().draw().unwrap();
}

/// Trains the PPO agent in the synthetic environment.
fn train() {
    let mut avg_rewards = vec![];
    let mut policy_losses = vec![];
    let mut value_losses = vec![];

    let env = SyntheticEnv::new(NPROCS, OBSERVATION_DIM);
    let device = tch::Device::cuda_if_available();
    let vs = nn::VarStore::new(device);
    let model = model(&vs.root(), ACTION_DIM);
    let mut opt = nn::Adam::default().build(&vs, 1e-4).unwrap();

    let mut total_rewards = 0f64;
    let mut total_episodes = 0f64;

    for update_index in 0..UPDATES {
        let observations = env.reset();
        let states = Tensor::zeros([NSTEPS + 1, NPROCS, OBSERVATION_DIM], FLOAT_CPU);
        states.get(0).copy_(&observations);

        let rewards = Tensor::zeros([NSTEPS, NPROCS], FLOAT_CPU);
        let actions = Tensor::zeros([NSTEPS, NPROCS], INT64_CPU);
        let masks = Tensor::zeros([NSTEPS, NPROCS], FLOAT_CPU);
        let values = Tensor::zeros([NSTEPS, NPROCS], FLOAT_CPU);

        for step in 0..NSTEPS {
            let (critic, actor) = tch::no_grad(|| model(&states.get(step)));
            let probs = actor.softmax(-1, Kind::Float);
            let selected_actions = probs.multinomial(1, true).squeeze_dim(-1);

            let (next_obs, reward, done) = env.step(&selected_actions);

            total_rewards += f64::try_from((&reward * &done).sum(Kind::Float)).unwrap_or(0.0);
            total_episodes += f64::try_from(done.sum(Kind::Float)).unwrap_or(0.0);

            rewards.get(step).copy_(&reward);
            actions.get(step).copy_(&selected_actions);
            values.get(step).copy_(&critic.squeeze_dim(-1));
            masks.get(step).copy_(&(1.0 - done.to_kind(Kind::Float)));
            states.get(step + 1).copy_(&next_obs);
        }

        avg_rewards.push(total_rewards / total_episodes);

        let advantages = {
            let returns = Tensor::zeros([NSTEPS + 1, NPROCS], FLOAT_CPU);
            returns.get(-1).copy_(&values.get(-1));
            for step in (0..NSTEPS).rev() {
                let ret = rewards.get(step) + GAMMA * returns.get(step + 1) * masks.get(step);
                returns.get(step).copy_(&ret);
            }
            returns.narrow(0, 0, NSTEPS).to_device(device) - values.to_device(device)
        };

        for _ in 0..OPTIM_EPOCHS {
            let idx = Tensor::randint(NSTEPS * NPROCS, [OPTIM_BATCHSIZE], INT64_CPU);
            let sampled_states = states.narrow(0, 0, NSTEPS).view([-1, OBSERVATION_DIM]).index_select(0, &idx);
            let sampled_actions = actions.view([-1]).index_select(0, &idx);
            let sampled_advantages = advantages.view([-1]).index_select(0, &idx);
        
            let (_critic, actor) = model(&sampled_states); // Prefix with underscore
            let log_probs = actor.log_softmax(-1, Kind::Float);
            let action_log_probs = log_probs.gather(1, &sampled_actions.unsqueeze(-1), false).squeeze_dim(-1);
        
            let value_loss = sampled_advantages.square().mean(Kind::Float);
            let policy_loss = -(sampled_advantages.detach() * action_log_probs).mean(Kind::Float)
                + ENTROPY_BONUS * log_probs.exp().sum(Kind::Float);
        
            policy_losses.push(policy_loss.double_value(&[]));
            value_losses.push(value_loss.double_value(&[]));
        
            let loss = value_loss * 0.5 + policy_loss;
        
            opt.zero_grad();
            loss.backward();
            opt.step();
        }
        
        if update_index % 10 == 0 {
            println!(
                "Update: {}, Avg Reward: {:.2}, Episodes: {:.0}",
                update_index,
                total_rewards / total_episodes,
                total_episodes
            );
            total_rewards = 0.;
            total_episodes = 0.;
        }
    }

    visualize(&avg_rewards, &policy_losses, &value_losses, "ppo_metrics.png");
}

/// Main function to run training.
fn main() {
    println!("Starting PPO training...");
    train();
    println!("Training complete.");
}

The PPO algorithm iteratively trains an agent to optimize its policy by balancing exploration and exploitation. During each training step, the agent collects trajectory data by interacting with the environment, storing states, actions, rewards, and value estimates. The policy loss is computed by comparing the updated policy to the old policy using a clipped objective function, ensuring controlled updates. Simultaneously, the value loss minimizes the difference between predicted and actual returns. These losses are combined and optimized using backpropagation. Regular updates to the policy and value networks are performed using mini-batch sampling over multiple epochs.

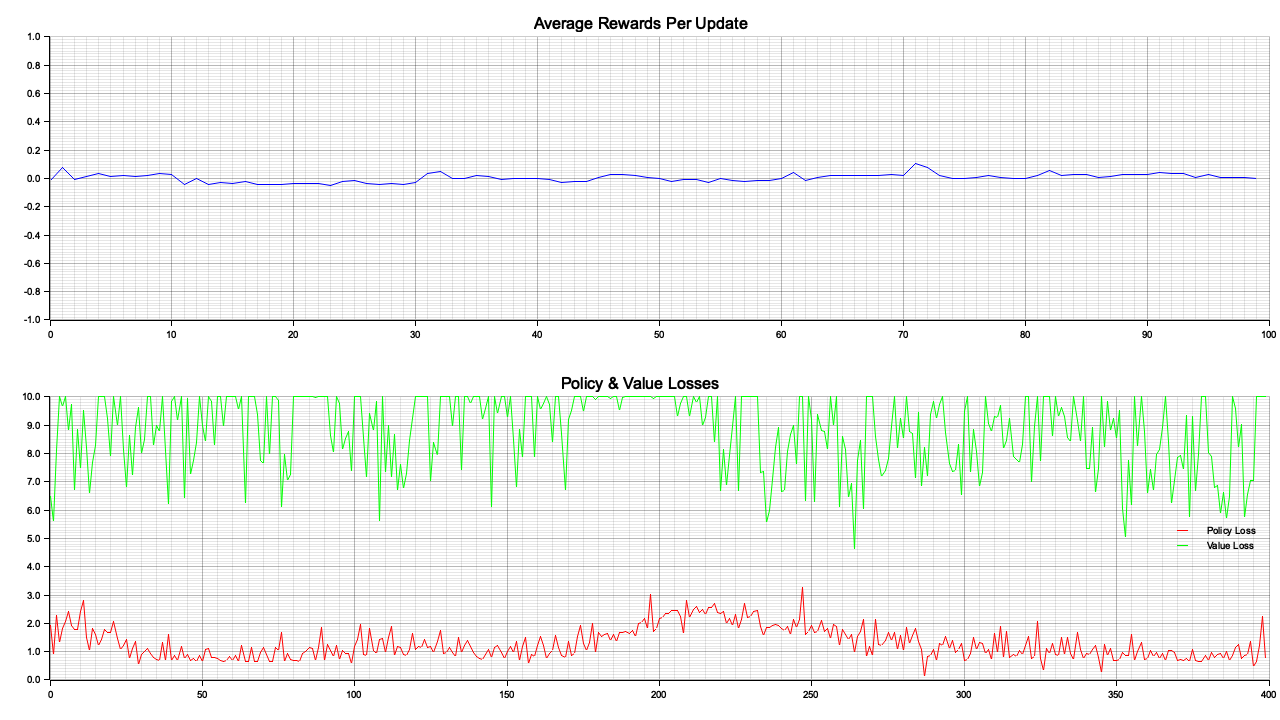
Figure 9: Plotters visualization of PPO training.

The visualizations provide key insights into the training dynamics. The "Average Rewards per Update" graph shows relatively stable average rewards over time, indicating that the agent's performance is consistent and does not exhibit significant degradation or instability. However, the values are generally low, suggesting the agent is operating in a challenging environment or requires further hyperparameter tuning. The "Policy & Value Losses" graph highlights the oscillatory nature of the policy loss, typical in reinforcement learning due to high variance in policy gradients. The value loss is lower and more stable, suggesting that the value network is learning to approximate returns effectively. These patterns indicate steady progress in learning while maintaining stability in updates.

Next, lets implement TRPO. The Trust Region Policy Optimization (TRPO) is a reinforcement learning algorithm that ensures stable and efficient policy updates by constraining the change in policy between consecutive updates. It uses a surrogate objective function that penalizes large policy changes, typically measured by the Kullback-Leibler (KL) divergence between the old and new policy distributions. TRPO employs a line search and trust region to optimize the policy while maintaining performance stability.

use tch::kind::{FLOAT_CPU, INT64_CPU};
use tch::{nn, Kind, Tensor};
use plotters::prelude::*;

// Constants
const OBSERVATION_DIM: i64 = 84 * 84;
const ACTION_DIM: i64 = 6; // Number of discrete actions
const NPROCS: i64 = 8;
const NSTEPS: i64 = 256;
const UPDATES: i64 = 100; // Reduced for demo purposes
const GAMMA: f64 = 0.99;

/// Synthetic environment to simulate agent interactions.
struct SyntheticEnv {
    nprocs: i64,
    observation_dim: i64,
}

impl SyntheticEnv {
    pub fn new(nprocs: i64, observation_dim: i64) -> Self {
        Self {
            nprocs,
            observation_dim,
        }
    }

    pub fn reset(&self) -> Tensor {
        Tensor::rand([self.nprocs, self.observation_dim], FLOAT_CPU)
    }

    pub fn step(&self, _actions: &Tensor) -> (Tensor, Tensor, Tensor) {
        let next_obs = Tensor::rand([self.nprocs, self.observation_dim], FLOAT_CPU);
        let rewards = Tensor::rand([self.nprocs], FLOAT_CPU)
            .f_mul_scalar(2.0).unwrap()
            .f_sub_scalar(1.0).unwrap(); // Rewards in [-1, 1]
        let dones = Tensor::rand([self.nprocs], FLOAT_CPU).gt(0.95); // 5% chance to end
        (next_obs, rewards, dones)
    }
}

/// Defines the neural network model for the TRPO agent.
fn model(p: &nn::Path, action_dim: i64) -> (nn::Sequential, nn::Linear, nn::Linear) {
    let base = nn::seq()
        .add(nn::linear(p / "l1", OBSERVATION_DIM, 256, Default::default()))
        .add(nn::layer_norm(p / "ln1", vec![256], Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(p / "l2", 256, 128, Default::default()))
        .add(nn::layer_norm(p / "ln2", vec![128], Default::default()))
        .add_fn(|x| x.relu());
    let critic = nn::linear(p / "critic", 128, 1, Default::default());
    let actor = nn::linear(p / "actor", 128, action_dim, Default::default());
    (base, critic, actor)
}

/// Computes the generalized advantage estimation (GAE).
fn compute_gae(rewards: &Tensor, values: &Tensor, masks: &Tensor, gamma: f64, lambda: f64) -> Tensor {
    let num_steps = rewards.size()[0];
    let num_envs = rewards.size()[1];
    
    let device = rewards.device(); // Ensure the device matches `rewards`

    let mut next_adv = Tensor::zeros([num_envs], (rewards.kind(), device)); // Shape [NPROCS]
    let gae = Tensor::zeros_like(rewards); // Shape [NSTEPS, NPROCS]
    
    for t in (0..num_steps).rev() {
        let delta = if t == num_steps - 1 {
            rewards.get(t) - values.get(t)
        } else {
            rewards.get(t)
                + gamma * values.get(t + 1) * masks.get(t)
                - values.get(t)
        };
        
        // Expand `next_adv` to match the shape of `delta` before addition
        next_adv = delta + gamma * lambda * masks.get(t) * next_adv;
        gae.get(t).copy_(&next_adv);
    }
    
    gae
}


/// Visualizes metrics using Plotters.
fn visualize(
    rewards: &[f64],
    policy_losses: &[f64],
    kl_divergences: &[f64],
    filename: &str,
) {
    let root = BitMapBackend::new(filename, (1280, 720)).into_drawing_area();
    root.fill(&WHITE).unwrap();
    let (upper, lower) = root.split_vertically(360);

    let mut rewards_chart = ChartBuilder::on(&upper)
        .caption("Average Rewards Per Update", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..rewards.len(), -1.0..1.0)
        .unwrap();
    rewards_chart.configure_mesh().draw().unwrap();
    rewards_chart
        .draw_series(LineSeries::new(
            (0..).zip(rewards.iter().cloned()),
            &BLUE,
        ))
        .unwrap();

    let mut losses_chart = ChartBuilder::on(&lower)
        .caption("Policy Loss & KL Divergence", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..policy_losses.len(), 0.0..10.0)
        .unwrap();
    losses_chart.configure_mesh().draw().unwrap();
    losses_chart
        .draw_series(LineSeries::new(
            (0..).zip(policy_losses.iter().cloned()),
            &RED,
        ))
        .unwrap()
        .label("Policy Loss")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 10, y)], &RED));
    losses_chart
        .draw_series(LineSeries::new(
            (0..).zip(kl_divergences.iter().cloned()),
            &GREEN,
        ))
        .unwrap()
        .label("KL Divergence")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 10, y)], &GREEN));
    losses_chart.configure_series_labels().draw().unwrap();
}

/// Trains the TRPO agent in the synthetic environment.
/// Trains the TRPO agent in the synthetic environment.
fn train_trpo() {
    let mut avg_rewards = vec![];
    let mut policy_losses = vec![];
    let mut kl_divergences = vec![];

    let env = SyntheticEnv::new(NPROCS, OBSERVATION_DIM);
    let device = tch::Device::cuda_if_available();
    let vs = nn::VarStore::new(device);
    let (base, critic, actor) = model(&vs.root(), ACTION_DIM);

    let mut total_rewards = 0f64;
    let mut total_episodes = 0f64;

    for _update_index in 0..UPDATES {
        let observations = env.reset();
        let states = Tensor::zeros([NSTEPS + 1, NPROCS, OBSERVATION_DIM], FLOAT_CPU);
        states.get(0).copy_(&observations);

        let rewards = Tensor::zeros([NSTEPS, NPROCS], FLOAT_CPU);
        let actions = Tensor::zeros([NSTEPS, NPROCS], INT64_CPU);
        let masks = Tensor::zeros([NSTEPS, NPROCS], FLOAT_CPU);
        let values = Tensor::zeros([NSTEPS, NPROCS], FLOAT_CPU);

        for step in 0..NSTEPS {
            let base_out = states.get(step).apply(&base);
            let probs = base_out.apply(&actor).softmax(-1, Kind::Float);
            let selected_actions = probs.multinomial(1, true).squeeze_dim(-1);

            let (next_obs, reward, done) = env.step(&selected_actions);

            total_rewards += f64::try_from((&reward * &done).sum(Kind::Float)).unwrap_or(0.0);
            total_episodes += f64::try_from(done.sum(Kind::Float)).unwrap_or(0.0);

            rewards.get(step).copy_(&reward);
            actions.get(step).copy_(&selected_actions);
            masks.get(step).copy_(&(1.0 - done.to_kind(Kind::Float)));
            values.get(step).copy_(&base_out.apply(&critic).squeeze_dim(-1));
            states.get(step + 1).copy_(&next_obs);
        }

        avg_rewards.push(total_rewards / total_episodes);

        let advantages = compute_gae(&rewards, &values, &masks, GAMMA, 0.95);

        // Save old probabilities before updating the policy
        let old_probs = states
            .narrow(0, 0, NSTEPS)
            .view([-1, OBSERVATION_DIM])
            .apply(&base)
            .apply(&actor)
            .softmax(-1, Kind::Float);

        // Clone `old_probs` to avoid move errors
        let old_probs_clone = old_probs.shallow_clone();

        // Policy update using the advantages
        let idx = Tensor::randint(NSTEPS * NPROCS, [256], INT64_CPU); // Sample 256 points
        let sampled_states = states.narrow(0, 0, NSTEPS).view([-1, OBSERVATION_DIM]).index_select(0, &idx);
        let sampled_actions = actions.view([-1]).index_select(0, &idx);
        let sampled_advantages = advantages.view([-1]).index_select(0, &idx);

        let sampled_probs = sampled_states
            .apply(&base)
            .apply(&actor)
            .softmax(-1, Kind::Float);

        let log_probs = sampled_probs.log_softmax(-1, Kind::Float);
        let action_log_probs = log_probs.gather(1, &sampled_actions.unsqueeze(-1), false).squeeze_dim(-1);

        let policy_loss = -(sampled_advantages.detach() * action_log_probs).mean(Kind::Float);
        policy_losses.push(policy_loss.double_value(&[]));

        // Apply TRPO constraints (e.g., KL divergence target)
        let new_probs = states
            .narrow(0, 0, NSTEPS)
            .view([-1, OBSERVATION_DIM])
            .apply(&base)
            .apply(&actor)
            .softmax(-1, Kind::Float);

        // Use the cloned `old_probs` to compute KL divergence
        let kl_divergence = ((old_probs_clone * (old_probs.log() - new_probs.log())).sum(Kind::Float)).mean(Kind::Float);
        kl_divergences.push(kl_divergence.double_value(&[]));

        println!(
            "Update: {}, Avg Reward: {:.2}, KL Divergence: {:.4}, Policy Loss: {:.4}",
            _update_index,
            total_rewards / total_episodes,
            kl_divergence.double_value(&[]),
            policy_loss.double_value(&[])
        );

        total_rewards = 0.;
        total_episodes = 0.;
    }

    visualize(&avg_rewards, &policy_losses, &kl_divergences, "trpo_metrics.png");
}

/// Main function to run training.
fn main() {
    println!("Starting TRPO training...");
    train_trpo();
    println!("Training complete.");
}

TRPO begins by collecting trajectories from the environment using the current policy. It calculates advantages using the Generalized Advantage Estimation (GAE) method to measure the relative quality of actions. The policy is updated by optimizing the surrogate objective under a KL divergence constraint to limit policy changes. This ensures that the learning remains within a "trust region," balancing exploration and exploitation. The value function (critic) is also updated to estimate future rewards more accurately.

Figure 10: Plotters visualization of TRPO training.

\ The "Average Rewards Per Update" chart shows a generally stable trend with slight fluctuations, indicating that the TRPO algorithm maintains consistent learning across updates. The "Policy Loss & KL Divergence" chart highlights low and stable KL divergence values, suggesting that the policy changes are well-regulated within the trust region. The policy loss remains minimal, showing efficient optimization and stability in training. Overall, these visualizations affirm that TRPO effectively stabilizes learning while optimizing the agent's policy.

The Asynchronous Advantage Actor-Critic (A3C) model is a state-of-the-art reinforcement learning algorithm designed to efficiently handle complex environments by utilizing parallel training. Unlike traditional single-threaded training methods, A3C leverages multiple workers (threads or processes), each interacting with its own instance of the environment to independently collect experience. These workers asynchronously update a shared global model, allowing for diverse exploration of the environment and faster convergence. A3C uses two neural network components: a policy network (actor) that outputs action probabilities and a value network (critic) that estimates the expected return. This dual architecture allows the model to learn both an optimal policy and value function simultaneously, achieving stable and efficient learning.

One of the key innovations of A3C is its use of the Generalized Advantage Estimation (GAE) to compute the advantages, which balance bias and variance during policy updates. By utilizing a multi-threaded approach and asynchronous updates, A3C avoids the need for a replay buffer, commonly used in other methods like DQN, thereby reducing memory overhead. This makes it particularly suited for environments with continuous or high-dimensional state spaces. The A3C model achieves high performance on a wide range of tasks, from video games to robotics simulations, demonstrating its versatility and robustness.

use tch::kind::{FLOAT_CPU};
use tch::{nn, nn::OptimizerConfig, Kind, Tensor};
use std::sync::{Arc, Mutex};
use std::thread;
use plotters::prelude::*;

// Constants
const OBSERVATION_DIM: i64 = 84 * 84; // Dimension of the observation space
const ACTION_DIM: i64 = 6; // Number of discrete actions
const NPROCS: i64 = 8; // Number of parallel workers
const NSTEPS: i64 = 256; // Number of steps per update
const UPDATES: i64 = 100; // Number of updates during training
const GAMMA: f64 = 0.99; // Discount factor for rewards

/// Synthetic environment to simulate agent interactions.
struct SyntheticEnv {
    nprocs: i64,
    observation_dim: i64,
}

impl SyntheticEnv {
    pub fn new(nprocs: i64, observation_dim: i64) -> Self {
        Self {
            nprocs,
            observation_dim,
        }
    }

    /// Reset the environment and return initial observations.
    pub fn reset(&self) -> Tensor {
        Tensor::rand([self.nprocs, self.observation_dim], FLOAT_CPU)
    }

    /// Simulate a step in the environment given actions.
    pub fn step(&self, _actions: &Tensor) -> (Tensor, Tensor, Tensor) {
        let next_obs = Tensor::rand([self.nprocs, self.observation_dim], FLOAT_CPU);
        let rewards = Tensor::rand([self.nprocs], FLOAT_CPU)
            .f_mul_scalar(2.0).unwrap()
            .f_sub_scalar(1.0).unwrap(); // Rewards in [-1, 1]
        let dones = Tensor::rand([self.nprocs], FLOAT_CPU).gt(0.95); // 5% chance to terminate
        (next_obs, rewards, dones)
    }
}

/// Defines the neural network model for the A3C agent.
fn model(p: &nn::Path, action_dim: i64) -> (nn::Sequential, nn::Linear, nn::Linear) {
    let base = nn::seq()
        .add(nn::linear(p / "l1", OBSERVATION_DIM, 256, Default::default()))
        .add(nn::layer_norm(p / "ln1", vec![256], Default::default()))
        .add_fn(|x| x.relu())
        .add(nn::linear(p / "l2", 256, 128, Default::default()))
        .add(nn::layer_norm(p / "ln2", vec![128], Default::default()))
        .add_fn(|x| x.relu());
    let critic = nn::linear(p / "critic", 128, 1, Default::default());
    let actor = nn::linear(p / "actor", 128, action_dim, Default::default());
    (base, critic, actor)
}

/// Computes the Generalized Advantage Estimation (GAE).
fn compute_gae(rewards: &Tensor, values: &Tensor, masks: &Tensor, gamma: f64, lambda: f64) -> Tensor {
    let num_steps = rewards.size()[0];
    let num_envs = rewards.size()[1];

    let device = rewards.device(); // Ensure the device matches `rewards`

    let mut next_adv = Tensor::zeros([num_envs], (rewards.kind(), device)); // Shape [NPROCS]
    let gae = Tensor::zeros_like(rewards); // Shape [NSTEPS, NPROCS]

    for t in (0..num_steps).rev() {
        let delta = if t == num_steps - 1 {
            rewards.get(t) - values.get(t)
        } else {
            rewards.get(t)
                + gamma * values.get(t + 1) * masks.get(t)
                - values.get(t)
        };
        next_adv = delta + gamma * lambda * masks.get(t) * next_adv;
        gae.get(t).copy_(&next_adv);
    }

    gae
}

/// A3C Worker function for training a local model and updating the global model.
fn a3c_worker(
    id: usize,
    global_model: Arc<Mutex<nn::VarStore>>,
    global_rewards: Arc<Mutex<Vec<f64>>>,
) {
    let env = SyntheticEnv::new(NPROCS, OBSERVATION_DIM);
    let device = tch::Device::cuda_if_available();
    let vs = nn::VarStore::new(device);
    let (base, critic, actor) = model(&vs.root(), ACTION_DIM);
    let mut opt = nn::Adam::default().build(&vs, 1e-4).unwrap();

    for update_index in 0..UPDATES {
        let observations = env.reset();
        let mut states = vec![observations.shallow_clone()]; // Store states in a vector

        let mut rewards_vec = Vec::new();
        let mut actions_vec = Vec::new();
        let mut masks_vec = Vec::new();
        let mut values_vec = Vec::new();

        let mut total_rewards = 0f64;

        // Collect rollout data
        for _step in 0..NSTEPS {
            let current_state = states.last().unwrap();
            let base_out = current_state.apply(&base);
            let probs = base_out.apply(&actor).softmax(-1, Kind::Float);
            let selected_actions = probs.multinomial(1, true).squeeze_dim(-1);

            let (next_obs, reward, done) = env.step(&selected_actions);

            total_rewards += f64::try_from(reward.sum(Kind::Float)).unwrap_or(0.0);

            rewards_vec.push(reward);
            actions_vec.push(selected_actions);
            masks_vec.push(1.0 - done.to_kind(Kind::Float));
            values_vec.push(base_out.apply(&critic).squeeze_dim(-1));
            states.push(next_obs);
        }

        // Process collected data
        let rewards = Tensor::stack(&rewards_vec, 0);
        let actions = Tensor::stack(&actions_vec, 0);
        let masks = Tensor::stack(&masks_vec, 0);
        let values = Tensor::stack(&values_vec, 0);

        let advantages = compute_gae(&rewards, &values, &masks, GAMMA, 0.95);

        // Flatten tensors for policy update
        let actions_flat = actions.view([-1]); // Shape: [NSTEPS * NPROCS]
        let advantages_flat = advantages.view([-1]); // Shape: [NSTEPS * NPROCS]

        let all_states = Tensor::stack(&states[..NSTEPS as usize], 0)
            .view([-1, OBSERVATION_DIM]); // Shape: [NSTEPS * NPROCS, OBSERVATION_DIM]
        let all_probs = all_states
            .apply(&base)
            .apply(&actor)
            .softmax(-1, Kind::Float); // Shape: [NSTEPS * NPROCS, ACTION_DIM]

        // Compute log probabilities
        let log_probs = all_probs.log_softmax(-1, Kind::Float);
        let action_log_probs = log_probs
            .gather(1, &actions_flat.unsqueeze(-1), false) // Shape: [NSTEPS * NPROCS, 1]
            .squeeze_dim(-1); // Shape: [NSTEPS * NPROCS]

        // Compute policy loss
        let policy_loss = -(advantages_flat.detach() * action_log_probs).mean(Kind::Float);

        // Compute value loss
        let value_loss = advantages_flat.square().mean(Kind::Float);

        // Combine losses
        let loss = policy_loss + value_loss;

        // Update global model
        if let Ok(_global_vstore) = global_model.lock() {
            opt.zero_grad();
            loss.backward();
            opt.step();

            println!(
                "Worker {}: Update {}, Reward {:.2}",
                id, update_index, total_rewards
            );
        }

        // Update global rewards
        if let Ok(mut global_rewards_locked) = global_rewards.lock() {
            global_rewards_locked.push(total_rewards);
        }
    }
}

/// Visualizes training metrics using Plotters.
fn visualize_rewards(rewards: &[f64], filename: &str) {
    let root = BitMapBackend::new(filename, (1280, 720)).into_drawing_area();
    root.fill(&WHITE).unwrap();

    let mut chart = ChartBuilder::on(&root)
        .caption("Rewards Over Time", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(40)
        .build_cartesian_2d(0..rewards.len(), -1.0..1.0)
        .unwrap();

    chart.configure_mesh().draw().unwrap();

    chart
        .draw_series(LineSeries::new(
            rewards.iter().enumerate().map(|(x, y)| (x, *y)),
            &RED,
        ))
        .unwrap();
}

/// Main function to run training.
fn main() {
    let global_model = Arc::new(Mutex::new(nn::VarStore::new(tch::Device::cuda_if_available())));
    let global_rewards = Arc::new(Mutex::new(vec![]));

    let mut handles = vec![];
    for id in 0..NPROCS as usize {
        let global_model = Arc::clone(&global_model);
        let global_rewards = Arc::clone(&global_rewards);

        let handle = thread::spawn(move || a3c_worker(id, global_model, global_rewards));
        handles.push(handle);
    }

    for handle in handles {
        handle.join().unwrap();
    }

    // Visualization
    if let Ok(global_rewards) = global_rewards.lock() {
        visualize_rewards(&global_rewards, "rewards.png");
    }

    println!("A3C training complete.");
}

The code implements an A3C model in Rust using the tch library for deep learning operations. The global model is initialized and shared among NPROCS workers (parallel threads). Each worker interacts with its own synthetic environment, simulating agent interactions by resetting the environment, taking actions, and collecting rewards and states over multiple steps (NSTEPS). The workers compute policy losses (using the log-probabilities of actions weighted by the advantages) and value losses (squared difference between predicted and actual returns) for each update. These losses are combined and backpropagated through the worker's local model. Periodically, the local model's gradients are applied to update the shared global model. Throughout training, rewards collected by workers are stored in a shared structure and visualized using the plotters library, allowing tracking of learning progress.

A3C is inherently suited for a multi-threaded environment like Rust, where threads can run separate agents in parallel. Using Rust’s thread and async features, we can design an A3C framework where each thread independently collects experiences and updates a shared global model asynchronously. Key aspects include efficient thread communication and locking mechanisms to prevent data races.

PPO, TRPO, and A3C represent powerful tools for addressing the challenges of stability, efficiency, and scalability in DRL. By implementing these advanced algorithms in Rust, we can harness the language’s performance and safety guarantees to build robust DRL systems capable of tackling complex tasks. As we explore these methods further, their practical applications in domains like robotics, autonomous navigation, and resource management become increasingly evident, showcasing the transformative potential of DRL in real-world scenarios.

16.5. Challenges and Best Practices in Deep Reinforcement Learning link

Deep Reinforcement Learning (DRL) holds immense promise for solving complex decision-making tasks, but it comes with a set of challenges that require thoughtful strategies to overcome. Issues such as sample inefficiency, instability during training, and high variance in learning dynamics are pervasive in DRL algorithms. Moreover, the complexity of hyperparameter tuning and the variability in environments make the development and deployment of robust DRL systems a non-trivial endeavor. This section delves into the challenges of DRL, explores best practices for addressing these challenges, and provides practical guidance for implementing these strategies in Rust.

One of the most significant challenges in DRL is sample inefficiency. Unlike supervised learning, where the dataset is fixed, DRL agents must collect their training data through interactions with the environment. This process can be slow and expensive, especially in environments with sparse rewards, where meaningful feedback is infrequent. Additionally, DRL models often suffer from instability due to the iterative nature of policy updates, where small changes can lead to drastic shifts in behavior. High variance in the learning signal, especially in stochastic environments, further complicates the convergence of DRL algorithms, requiring robust methods to stabilize and regularize the learning process.

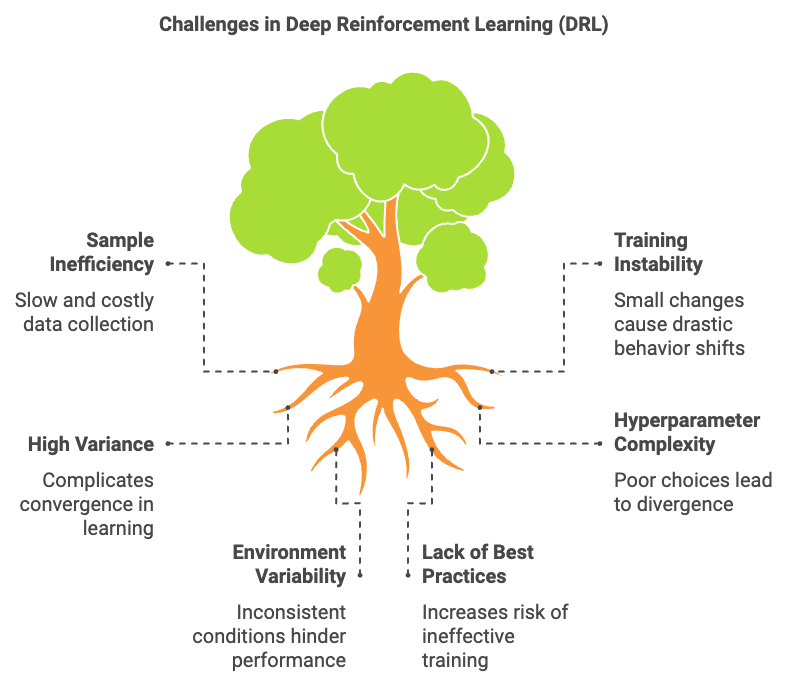
Figure 11: Key challenges in implementing advanced DRL models.

Hyperparameters in DRL—such as learning rates, discount factors ($\gamma$), exploration rates, and batch sizes—have a profound impact on model performance. Selecting appropriate values is critical, as suboptimal choices can lead to divergence or slow convergence. For example, a learning rate that is too high may cause the model to oscillate without settling on an optimal policy, while a discount factor that is too low may overly prioritize short-term rewards. Systematic experimentation and optimization of these parameters are essential for effective training.

Best practices in DRL focus on improving stability, efficiency, and generalization. Techniques such as reward shaping, experience replay, and target networks have become standard tools for addressing challenges in DRL. Reward shaping involves modifying the reward function to provide more frequent feedback, guiding the agent toward desired behaviors. Experience replay, as discussed earlier, helps break correlations in the data and improves sample efficiency. Target networks decouple the learning signal, reducing the risk of instability during training. By integrating these techniques, practitioners can build more robust DRL models.

Reward shaping is a method of augmenting the reward function to make learning more efficient. For instance, instead of only providing a reward when an agent reaches a goal state, intermediate rewards can be introduced to guide the agent along the desired path. Mathematically, if $R(s, a, s')$ is the original reward function, a shaped reward function $R'(s, a, s')$ can be defined as:

$$ R'(s, a, s') = R(s, a, s') + \phi(s') - \phi(s), $$

where $\phi(s)$ is a potential function that provides additional guidance. This approach ensures that the shaping does not alter the optimal policy while accelerating learning.

Effective exploration is critical in DRL, as the agent must balance the trade-off between exploring new actions and exploiting known rewarding actions. Techniques such as $\epsilon$-greedy exploration, where the agent selects a random action with probability $\epsilon$ and the optimal action otherwise, are simple yet effective. More advanced methods, like noisy networks or Boltzmann exploration, introduce stochasticity directly into the policy, allowing for more dynamic exploration strategies.

Transfer learning leverages pre-trained models to accelerate learning in new environments. For instance, a policy trained in one environment can serve as an initialization for a similar environment, reducing the time required to adapt. Formally, if $\pi_{\theta_1}$ is a policy learned in environment $E_1$, transfer learning initializes a new policy $\pi_{\theta_2}$ for environment $E_2$ such that $\theta_2 \approx \theta_1$. Fine-tuning $\theta_2$ on $E_2$ allows the agent to learn more efficiently by building on prior knowledge.

Below is a simplified implementation of reward shaping for a sparse-reward environment, such as a grid-world task.

fn reward_shaping(original_reward: f32, current_state: &Tensor, next_state: &Tensor) -> f32 {
    let potential = |state: &Tensor| -> f32 {
        // Define a potential function based on the distance to the goal
        let goal = Tensor::of_slice(&[10.0, 10.0]);
        -state.sub(&goal).pow(2).sum(Kind::Float).double_value(&[])
    };

    original_reward + potential(next_state) - potential(current_state)
}

This reward shaping function adds potential-based guidance to the original reward, encouraging the agent to move closer to the goal state.

The following example demonstrates implementing a noisy exploration strategy using Gaussian noise.

fn noisy_action(action: &Tensor, noise_scale: f32) -> Tensor {
    let noise = Tensor::randn_like(action) * noise_scale;
    action + noise
}

// Example usage:
let action = Tensor::of_slice(&[0.5, -0.2]); // Example action
let noisy_action = noisy_action(&action, 0.1); // Add Gaussian noise

This technique introduces randomness directly into the action selection process, encouraging exploration in continuous action spaces.

To implement transfer learning, we can save the weights of a pre-trained model and use them to initialize a new model.

use tch::{nn, nn::ModuleT, Device};

fn transfer_model_weights(src: &nn::VarStore, dest: &mut nn::VarStore) {
    dest.copy(src).expect("Failed to copy model weights");
}

// Example usage:
let src_model = nn::VarStore::new(Device::cuda_if_available());
let dest_model = nn::VarStore::new(Device::cuda_if_available());
// Assume src_model is pre-trained
transfer_model_weights(&src_model, &mut dest_model);

This approach enables faster adaptation to new tasks by leveraging previously learned policies.

Deep reinforcement learning presents a unique set of challenges, but by adopting best practices such as reward shaping, advanced exploration strategies, and transfer learning, practitioners can address these effectively. Implementing these strategies in Rust ensures a high-performance, reliable foundation for DRL applications. Through thoughtful design and rigorous experimentation, DRL practitioners can unlock the full potential of these techniques in real-world tasks ranging from robotics to autonomous navigation. The robustness of Rust’s ecosystem further empowers developers to build scalable and efficient DRL systems, paving the way for innovation in the field.

10.6. Conclusion link

Chapter 10 emphasizes the transformative potential of Deep Reinforcement Learning, highlighting how the combination of deep learning and reinforcement learning enables the development of intelligent agents capable of solving complex tasks in high-dimensional spaces. By mastering the implementation of DRL techniques using Rust, readers will be well-equipped to tackle advanced reinforcement learning challenges, applying state-of-the-art methods to real-world problems with confidence and precision.

10.6.1. Further Learning with GenAI link

These prompts are designed to guide you through a deep exploration of Deep Reinforcement Learning (DRL) concepts, techniques, and practical implementations using Rust.

• Explain the fundamental principles of Deep Reinforcement Learning (DRL). How does DRL differ from traditional reinforcement learning, and what advantages does it offer for handling high-dimensional state and action spaces? Implement a basic DRL model in Rust and discuss its significance.

• Discuss the role of function approximation in DRL. How do neural networks serve as function approximators in DRL, and what challenges arise from using them? Implement a neural network-based function approximator in Rust and analyze its impact on the learning process.

• Explore the differences between model-free and model-based DRL methods. When is each approach most appropriate, and what are the trade-offs involved? Implement a simple model-free DRL algorithm in Rust and compare it with a model-based approach.

• Analyze the significance of experience replay in Deep Q-Networks (DQN). How does experience replay stabilize learning, and what are the benefits of reusing past experiences? Implement experience replay in Rust and observe its effects on training stability and efficiency.

• Discuss the concept of target networks in DQN. How do target networks prevent instability in training, and why are they crucial for successful DRL? Implement a target network in Rust for a DQN and analyze its impact on learning performance.

• Explore the limitations of vanilla DQN. What challenges, such as overestimation bias and sample inefficiency, affect the performance of DQN, and how can these issues be mitigated? Implement advanced DQN techniques like double DQN and dueling DQN in Rust to address these limitations.

• Examine the trade-off between bias and variance in policy gradient methods within DRL. How does this trade-off influence the convergence of policy gradient algorithms? Implement a policy gradient method in Rust and experiment with different strategies to manage this trade-off.

• Discuss the role of stochastic policies in policy gradient methods. How do stochastic policies enable exploration in continuous action spaces, and what are their advantages over deterministic policies? Implement a stochastic policy in Rust and analyze its impact on the learning process.

• Analyze the significance of entropy regularization in policy gradient methods. How does entropy regularization encourage exploration and prevent premature convergence? Implement entropy regularization in Rust and observe its effects on policy learning and stability.

• Explore the concept of actor-critic methods in DRL. How do actor-critic methods combine policy gradient with value function approximation, and what benefits do they offer? Implement a basic actor-critic algorithm in Rust and compare its performance with a pure policy gradient method.

• Discuss the role of advantage functions in actor-critic methods. How do advantage estimates reduce variance in policy gradient updates, and why are they important for efficient learning? Implement an advantage function in Rust and experiment with different actor-critic architectures.

• Examine the principles behind Proximal Policy Optimization (PPO) and Trust Region Policy Optimization (TRPO). How do these advanced DRL algorithms ensure stable policy updates, and what are their key differences? Implement PPO in Rust and compare its performance with TRPO in a complex DRL task.

• Analyze the importance of trust regions in TRPO. How do trust regions prevent large, destabilizing policy updates, and what impact do they have on learning stability? Implement a trust region in Rust for TRPO and observe its effects on policy optimization.

• Discuss the role of asynchronous updates in Asynchronous Advantage Actor-Critic (A3C). How do asynchronous updates improve learning efficiency, and what challenges do they introduce? Implement A3C in Rust and analyze its performance in a resource-constrained environment.

• Explore the challenges of applying DRL in high-dimensional state spaces, such as image-based environments. What techniques, such as convolutional neural networks (CNNs), can be used to handle high-dimensional inputs? Implement a DRL algorithm in Rust using CNNs and evaluate its performance on an image-based task.

• Discuss the significance of hyperparameter tuning in DRL. What are the key hyperparameters that influence the performance of DRL models, and how can they be optimized? Implement a Rust-based framework for hyperparameter tuning in a DRL algorithm and analyze the results.

• Examine the impact of reward shaping on DRL. How does modifying the reward function guide the learning process, and what are the potential benefits and drawbacks? Implement reward shaping in Rust for a challenging DRL task and evaluate its effects on policy learning.

• Explore the role of exploration strategies in DRL. How do different exploration techniques, such as epsilon-greedy or entropy regularization, influence the effectiveness of DRL algorithms? Implement and compare various exploration strategies in Rust to determine their impact on learning efficiency.

• Analyze the convergence properties of DRL algorithms in continuous action spaces. What factors influence convergence, and how can these algorithms be optimized for faster and more stable learning? Implement a Rust-based simulation to analyze the convergence behavior of a DRL algorithm in a complex environment.

• Discuss the ethical considerations of deploying DRL in real-world applications, such as autonomous vehicles or healthcare systems. What risks are associated with these applications, and how can they be mitigated? Implement a DRL algorithm in Rust for a real-world-inspired scenario and analyze the ethical implications of its deployment.

Let these prompts inspire you to push the boundaries of your learning, experiment with different approaches, and master the art of Deep Reinforcement Learning with confidence and precision.

10.6.2. Hands On Practices link

These exercises encourage hands-on experimentation and thorough engagement with the concepts, allowing readers to apply their knowledge practically.

Exercise 10.1: Implementing and Analyzing a Basic Deep Q-Network (DQN) link

Task:

• Implement a Deep Q-Network (DQN) in Rust for a high-dimensional task, such as playing a simple game like Pong or navigating a maze with visual inputs.

Challenge:

• Experiment with different neural network architectures and experience replay buffer sizes to optimize the performance of your DQN. Compare the effects of these variations on training stability and convergence speed.

• Analyze the impact of using target networks on the stability of the learning process, and discuss the results.

Exercise 10.2: Developing an Actor-Critic Algorithm for Continuous Control link

Task:

• Implement an Actor-Critic algorithm in Rust to solve a continuous control task, such as balancing a pole on a cart or controlling a robotic arm.

Challenge:

• Experiment with different architectures for the actor and critic networks. Explore how the choice of architecture influences the learning speed, stability, and final performance of the model.

• Compare the performance of the Actor-Critic method to that of a DQN on the same task, and analyze the advantages and limitations of each approach.

Exercise 10.3: Implementing Proximal Policy Optimization (PPO) for Complex Tasks link

Task:

• Implement the Proximal Policy Optimization (PPO) algorithm in Rust for a complex reinforcement learning task, such as navigating a 3D environment or controlling an agent in a dynamic simulation.

Challenge:

• Experiment with different clipping thresholds and entropy regularization techniques to optimize the performance of your PPO implementation. Analyze how these parameters affect the trade-off between exploration and exploitation.

• Compare the performance of PPO with that of a simpler policy gradient method, such as REINFORCE, and discuss the benefits of using PPO in complex tasks.

Exercise 10.4: Applying Convolutional Neural Networks (CNNs) in DRL link

Task:

• Implement a Deep Reinforcement Learning algorithm using Convolutional Neural Networks (CNNs) in Rust for an image-based task, such as object recognition in a visual navigation environment.

Challenge:

• Experiment with different CNN architectures and hyperparameters to optimize the performance of your DRL model. Analyze how the choice of architecture impacts the model's ability to learn from visual inputs.

• Compare the performance of your CNN-based DRL model with a non-CNN-based model on the same task, and discuss the advantages of using CNNs for high-dimensional input spaces.

Exercise 10.5: Exploring Reward Shaping in Deep Reinforcement Learning link

Task:

• Implement reward shaping in a DRL algorithm in Rust for a task with sparse rewards, such as navigating a maze or completing a sequence of actions in a game.

Challenge:

• Experiment with different reward shaping strategies to guide the learning process and improve efficiency. Analyze how modifying the reward function influences the agent's behavior and the overall learning performance.

• Compare the effectiveness of reward shaping with a standard reward structure, and discuss the potential benefits and risks of using reward shaping in reinforcement learning.

By implementing these techniques in Rust, you will deepen your understanding of how to apply DRL algorithms to solve complex tasks, enhance your ability to optimize and troubleshoot these models, and gain practical experience in building and evaluating DRL systems.