Chapter 19
Federated Deep Reinforcement Learning
"Alone we can do so little; together we can do so much." — Helen Keller
Chapter 19 delves into the sophisticated domain of Federated Deep Reinforcement Learning (FDRL), merging the principles of federated learning with the dynamic decision-making capabilities of reinforcement learning. This chapter meticulously explores the mathematical underpinnings of FDRL, including distributed optimization and consensus mechanisms, providing a solid foundation for understanding how decentralized agents can collaboratively learn without centralizing sensitive data. It examines core algorithms adapted for federated settings, such as Federated Averaging and Federated Policy Gradient methods, highlighting their theoretical foundations and practical implementations. A significant emphasis is placed on communication protocols, privacy-preserving techniques, and scalability strategies, showcasing how Rust's performance-oriented features facilitate the development of efficient and secure FDRL systems. Through a blend of rigorous theoretical discussions, conceptual frameworks, and hands-on coding examples in Rust, Chapter 19 equips readers with the knowledge and skills to design, implement, and evaluate federated reinforcement learning models across diverse and real-world applications.
19.1. Introduction to Federated Deep Reinforcement Learning
As the landscape of artificial intelligence continues to evolve, the integration of federated learning with reinforcement learning has introduced a transformative approach known as Federated Deep Reinforcement Learning (FDRL). This paradigm brings together the decentralized and privacy-preserving nature of federated learning with the interactive, decision-making capabilities of reinforcement learning, creating a framework that addresses some of the most pressing challenges in modern AI. By allowing agents to learn collaboratively across distributed environments while safeguarding sensitive data, FDRL embodies a shift towards scalable, ethical, and robust AI systems.
The evolution of FDRL is rooted in the independent development of its constituent fields. Federated learning emerged in the early 2010s as a response to increasing concerns over data privacy and the logistical challenges of centralized data aggregation. Organizations began exploring ways to train machine learning models directly on decentralized data sources, such as mobile devices or edge servers, without transferring sensitive data to central locations. This approach not only preserved privacy but also reduced the communication overhead associated with transmitting large datasets.
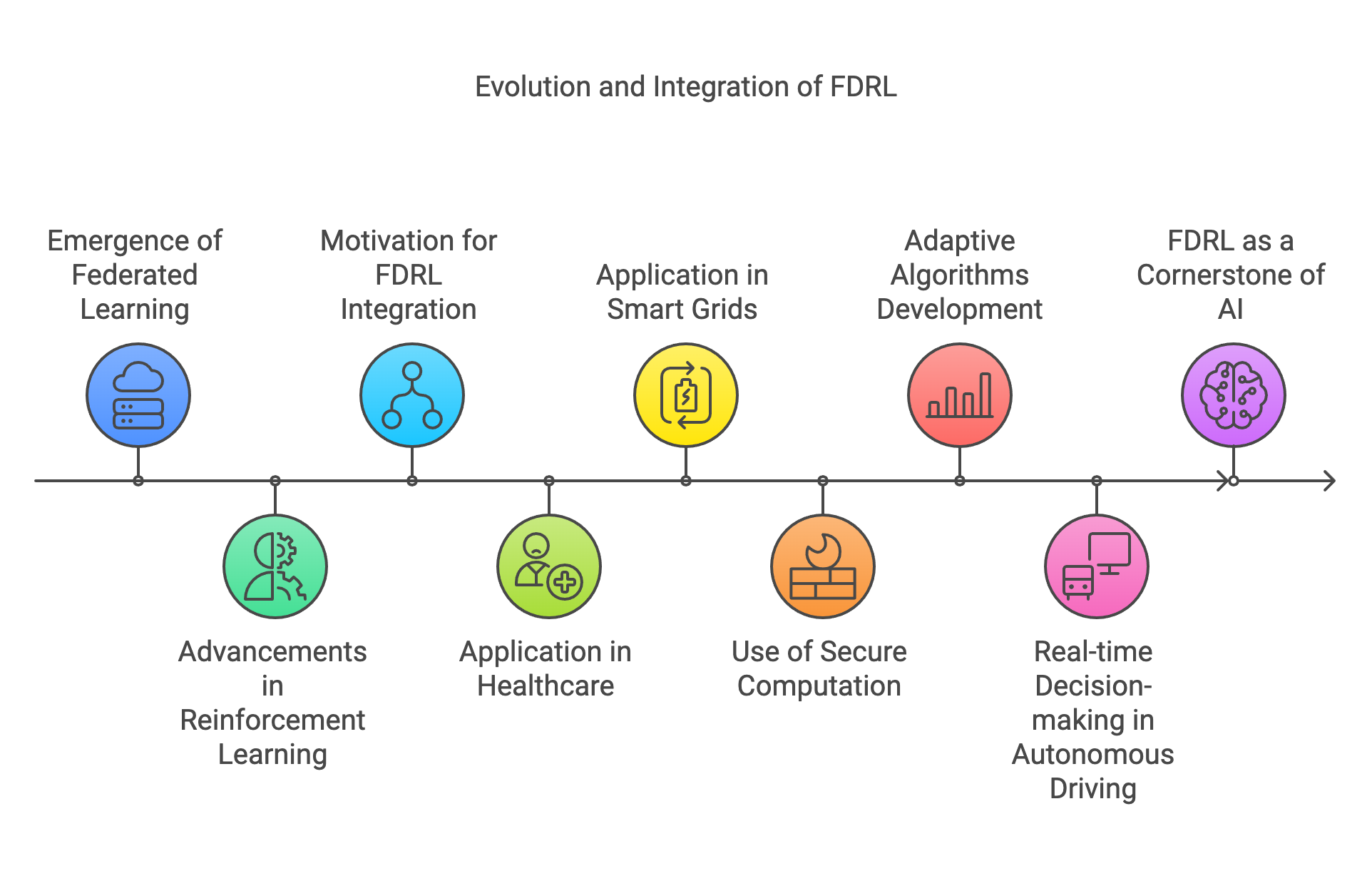
Figure 1: The natural evolution of federation learning in DRL.
Simultaneously, reinforcement learning advanced as a powerful framework for sequential decision-making, enabling agents to learn optimal policies through trial-and-error interactions with their environments. From its early applications in board games and robotics to its modern role in complex domains like healthcare and autonomous systems, RL demonstrated the ability to model and solve dynamic, interactive problems. However, traditional RL methods often relied on centralized architectures, where agents required access to extensive, aggregated data and computational resources.
The motivation for combining these two fields into FDRL arises from their complementary strengths and their ability to address the limitations of traditional centralized RL systems. In scenarios where data is distributed across multiple entities—such as hospitals, IoT devices, or autonomous vehicles—centralized RL is impractical due to data privacy concerns, bandwidth limitations, and regulatory constraints. Federated learning provides the solution by enabling agents to train locally and share only aggregated updates, ensuring that raw data remains secure and localized. By integrating reinforcement learning, FDRL extends this capability to interactive, decision-making tasks, allowing agents to optimize behaviors across decentralized systems.
One of the key motivations behind FDRL is its potential to democratize AI by harnessing the collective intelligence of distributed agents. In healthcare, for example, individual hospitals can train RL agents to optimize patient care protocols using their local data while contributing to a global model that benefits from diverse data sources. Similarly, in smart grids, distributed energy nodes can learn to balance loads and manage resources cooperatively without compromising sensitive usage data. This collaborative approach not only enhances the performance and generalization of the global model but also aligns with ethical principles by prioritizing privacy and inclusivity.
The evolution of FDRL has also been driven by advancements in distributed systems, secure computation, and scalable algorithms. Modern FDRL frameworks incorporate technologies such as secure multiparty computation (SMC) and differential privacy to ensure the confidentiality of agent updates. Additionally, adaptive algorithms have been developed to address the challenges of non-IID (non-independent and identically distributed) data, asynchronous updates, and varying computational capacities among agents. These innovations have made FDRL a viable solution for real-world applications where decentralization and privacy are critical.
Another significant motivation for FDRL is its potential to enable real-time, adaptive decision-making in dynamic and resource-constrained environments. In autonomous driving, for instance, vehicles equipped with RL agents can learn optimal driving strategies based on local conditions while contributing to a shared model that adapts to diverse traffic scenarios. In industrial automation, robots operating in distributed warehouses can collaboratively optimize logistics and resource allocation, improving efficiency and reducing costs.
As FDRL continues to mature, it is poised to become a cornerstone of AI systems designed for distributed, privacy-sensitive, and highly dynamic environments. By blending the strengths of federated and reinforcement learning, it addresses critical challenges in scalability, security, and adaptability, paving the way for a new era of collaborative intelligence. This chapter delves deeply into the theoretical foundations, key terminologies, and practical implementation strategies of FDRL, equipping readers with the knowledge and tools to leverage this paradigm in diverse domains. Through the use of Rust’s performance-oriented ecosystem, we demonstrate how to build and simulate decentralized learning environments, highlighting the unique capabilities of FDRL and its transformative potential.
Formally, consider a set of $K$ federated agents, each with its own local environment $E_k$. Each agent $k$ maintains a local policy $\pi_k$ and learns from its experiences within $E_k$. The objective of FDRL is to optimize a global policy $\pi$ that aggregates the knowledge from all local policies without necessitating the sharing of raw data between agents. This approach not only enhances scalability but also addresses privacy concerns by ensuring that sensitive data remains localized.
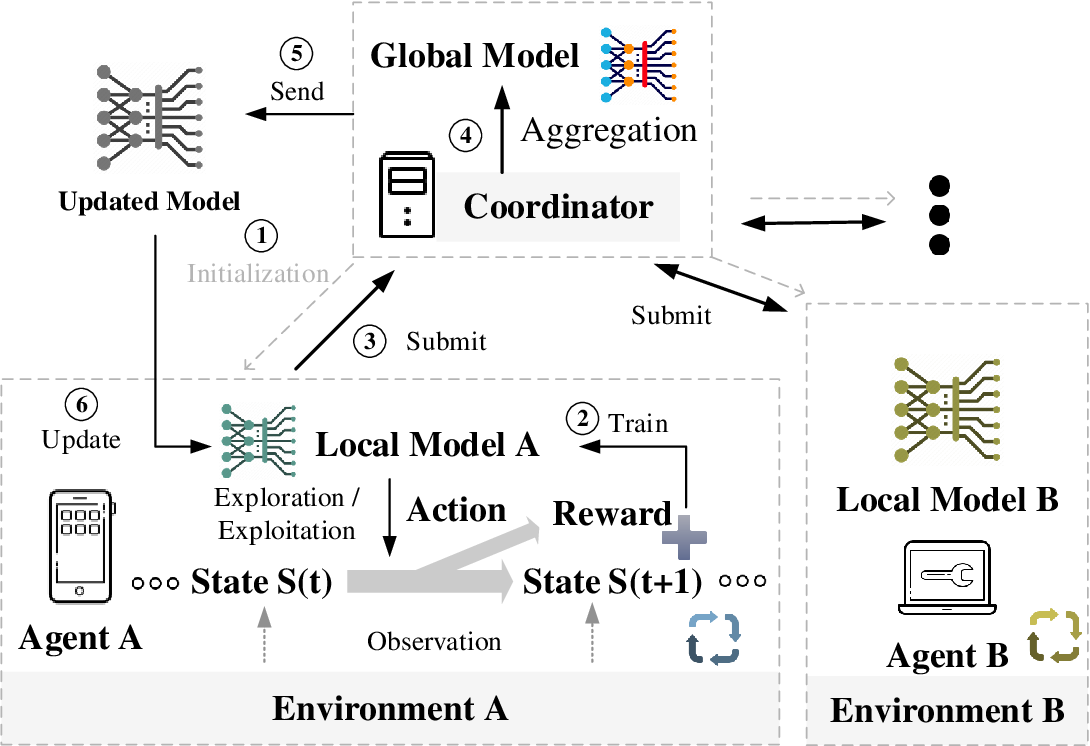
Figure 2: Illustration of Federated Deep Reinforcement Learning (FDRL).
The diagram illustrates the concept of FDRL, which enables distributed agents (e.g., Agent A and Agent B) to learn collaboratively while maintaining local control of their environments and data. Each agent interacts with its respective environment, observing states and executing actions that yield rewards. These interactions enable the training of a local model through reinforcement learning. Periodically, agents submit their locally updated models to a global coordinator. The coordinator aggregates the models, creating a global model that captures collective knowledge. This updated global model is then sent back to the agents, which integrate it into their local training processes. This decentralized approach leverages the advantages of shared learning while preserving privacy and reducing the need to centralize raw data. The cycle ensures efficient learning in a collaborative yet distributed manner, improving the performance of individual agents and the global system as a whole.
The mathematical underpinnings of FDRL are rooted in distributed optimization and consensus algorithms, which facilitate the coordination and synchronization of learning across multiple agents. The primary challenge in FDRL is to ensure that the aggregated global policy converges to an optimal or near-optimal solution despite the decentralized nature of data and computations.
Distributed Optimization: In FDRL, each agent $k$ aims to minimize a local loss function $L_k(\theta)$, where $\theta$ represents the parameters of the policy network. The global objective is to minimize the aggregated loss across all agents: $L(\theta) = \frac{1}{K} \sum_{k=1}^K L_k(\theta)$. This can be approached using algorithms such as Federated Averaging (FedAvg), where each agent performs local gradient descent updates on its loss function and periodically communicates the updated parameters to a central server for averaging: $\theta^{t+1} = \frac{1}{K} \sum_{k=1}^K \theta_k^{t}$, where $\theta_k^{t}$ are the parameters of agent $k$ at iteration $t$.
Consensus Algorithms: Consensus algorithms ensure that all agents agree on certain variables or states, facilitating coherent policy updates. One common approach is the decentralized consensus, where agents iteratively share and update their parameters based on their neighbors' states $\theta_k^{t+1} = \theta_k^{t} + \alpha \sum_{j \in \mathcal{N}_k} (\theta_j^{t} - \theta_k^{t})$, here, $\mathcal{N}_k$ denotes the set of neighboring agents of agent $k$, and $\alpha$ is the consensus step size. This iterative process drives the agents' parameters towards a common consensus value, promoting synchronization across the network.
Understanding the terminology specific to Federated Deep Reinforcement Learning (FDRL) is essential for grasping its operational dynamics and implementation strategies. Federated agents are individual learning entities that operate in their unique local environments. Each agent maintains its own policy and learns from its interactions without sharing raw data. Local models, trained by these agents, capture agent-specific policies and value functions based on localized data and experiences. These local models are aggregated into a global model, which combines knowledge from all agents, serving as a reference to synchronize and update local policies. Effective communication protocols enable agents to exchange critical information, such as model parameters or gradients, while maintaining synchronization. To ensure privacy during these exchanges, privacy-preserving techniques like differential privacy and secure multi-party computation are often employed. Consensus algorithms further facilitate coordinated policy updates by enabling agents to agree on variables or states, ensuring consistency across the federated network.
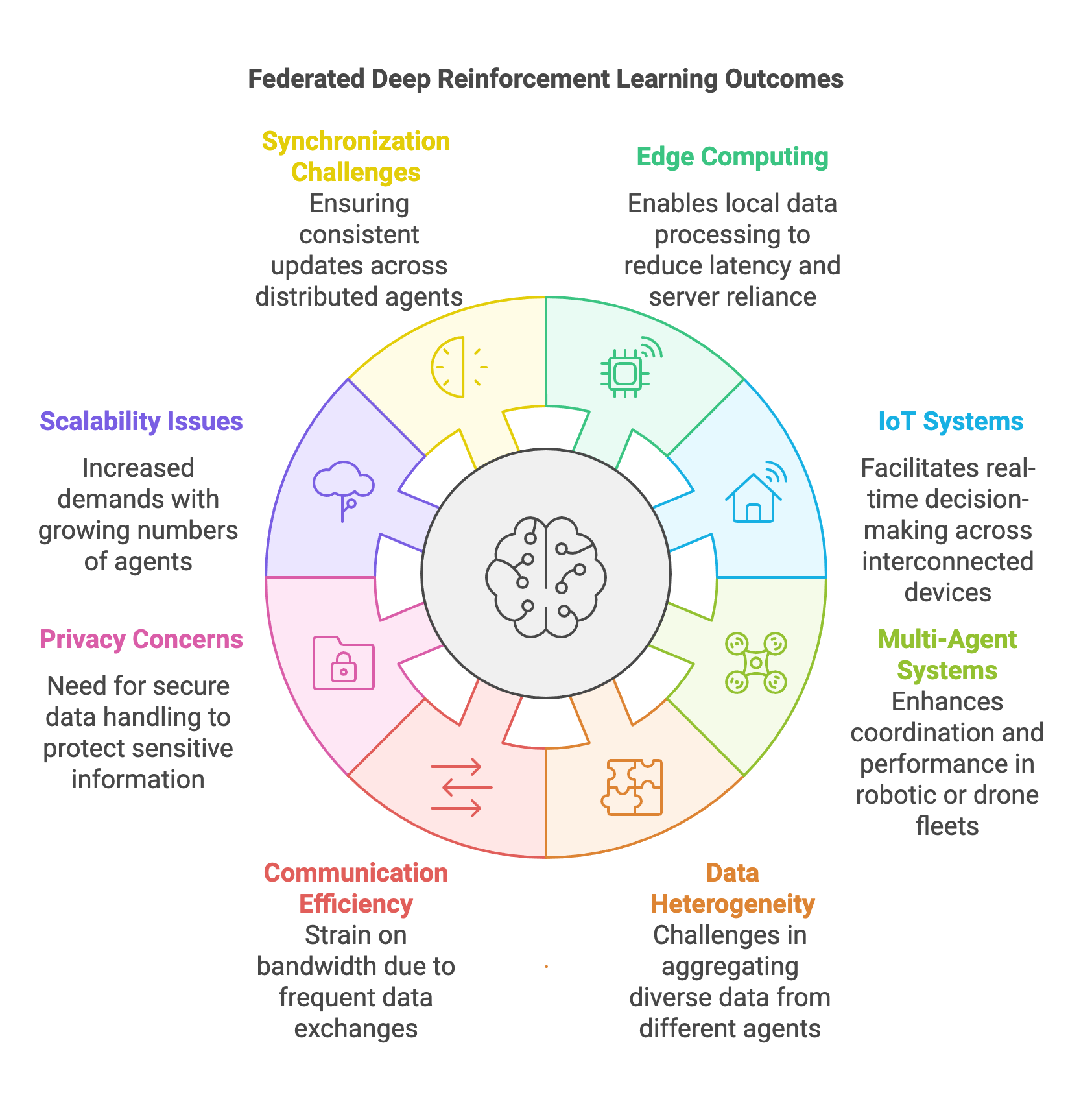
Figure 3: Scopes and applications of FDRL.
FDRL has immense potential in decentralized learning scenarios, especially in industries like edge computing, the Internet of Things (IoT), and multi-agent systems. In edge computing environments, data generated at the network’s periphery, such as from smartphones or IoT sensors, can be processed locally through FDRL, reducing latency and reliance on centralized servers. Similarly, IoT systems, with their vast network of interconnected devices, benefit from FDRL by enabling real-time decision-making and adaptability without overwhelming centralized infrastructure. In multi-agent systems like robotic swarms or drone fleets, FDRL allows individual agents to learn from their interactions while contributing to a collective learning objective, enhancing system coordination and performance.
Despite its benefits, FDRL poses challenges that must be addressed to realize its full potential. Data heterogeneity across agents often leads to non-identical, non-independent (non-IID) data distributions, complicating the aggregation of local models into a unified global model. Communication efficiency is another significant challenge, as frequent exchanges between agents and the central server can strain bandwidth and increase latency. Privacy concerns further complicate the system, necessitating techniques like secure aggregation to safeguard sensitive local data. Scalability is a critical concern as well, as the computational and communication demands of FDRL grow with the number of agents. Finally, ensuring synchronization and consistency across distributed agents is essential for effective learning, as delays or inconsistencies can impede convergence and lead to suboptimal outcomes.
FDRL also differs fundamentally from traditional centralized reinforcement learning (RL) in several aspects. Centralized RL relies on collecting and processing data in a unified environment, allowing for seamless optimization. FDRL, however, distributes data and computation across multiple agents, requiring decentralized learning strategies. This distributed approach makes FDRL inherently more scalable than centralized RL, which often faces bottlenecks as data volume and agent numbers increase. Privacy and security are another differentiating factor, with centralized RL requiring data aggregation that can raise concerns, whereas FDRL keeps data localized and employs privacy-preserving mechanisms. While centralized RL typically has minimal communication overhead post-data centralization, FDRL necessitates ongoing communication between agents and the central server, introducing additional overhead that needs efficient management. Lastly, FDRL offers greater flexibility and robustness to agent failures or network changes, whereas centralized RL systems are more prone to single points of failure and require substantial reconfiguration to adapt to changes.
Understanding these distinctions and challenges is critical for selecting and implementing the appropriate reinforcement learning paradigm based on the unique requirements of the application domain. FDRL’s ability to balance privacy, scalability, and decentralized learning positions it as a powerful approach for distributed systems and dynamic environments.
Implementing FDRL in Rust involves establishing a federated environment where multiple agents interact, learn, and communicate asynchronously. This code demonstrates a basic Federated Deep Reinforcement Learning (FDRL) simulation using Rust with asynchronous communication powered by the tokio crate. The system consists of a central server and multiple agents that communicate through asynchronous message passing. Each agent generates random model parameters and sends them to the central server, which then broadcasts these updates back to all agents, simulating the aggregation and synchronization of a global model in a federated learning context. The serde crate is used to serialize and deserialize data structures for seamless message exchanges between agents and the central server.
[dependencies]
anyhow = "1.0.93"
tokio = { version = "1.42", features = ["full"] }
serde = { version = "1.0", features = ["derive"] }
rand = { version = "0.8", features = ["std_rng"] }
use tokio::sync::mpsc;
use serde::{Serialize, Deserialize};
use tokio::task;
use std::collections::HashMap;
use rand::rngs::StdRng;
use rand::{Rng, SeedableRng};
#[derive(Serialize, Deserialize, Debug, Clone)]
struct ModelUpdate {
agent_id: usize,
parameters: Vec<f32>,
}
struct CentralServer {
receiver: mpsc::Receiver<ModelUpdate>,
senders: HashMap<usize, mpsc::Sender<ModelUpdate>>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelUpdate>, senders: HashMap<usize, mpsc::Sender<ModelUpdate>>) -> Self {
CentralServer { receiver, senders }
}
async fn run(&mut self) {
while let Some(update) = self.receiver.recv().await {
println!("Central Server received update from Agent {}", update.agent_id);
for (&agent_id, sender) in &self.senders {
sender.send(update.clone()).await.unwrap();
println!("Central Server sent aggregated parameters to Agent {}", agent_id);
}
}
}
}
#[tokio::main]
async fn main() {
let num_agents = 3;
let (tx, rx) = mpsc::channel(100);
let mut senders_map: HashMap<usize, mpsc::Sender<ModelUpdate>> = HashMap::new();
let mut receivers_map: HashMap<usize, mpsc::Receiver<ModelUpdate>> = HashMap::new();
for id in 0..num_agents {
let (tx_agent, rx_agent) = mpsc::channel(100);
senders_map.insert(id, tx_agent);
receivers_map.insert(id, rx_agent);
}
let mut server = CentralServer::new(rx, senders_map.clone());
task::spawn(async move {
server.run().await;
});
for id in 0..num_agents {
let tx_clone = tx.clone();
task::spawn(async move {
let seed = id as u64;
agent_task(id, tx_clone, seed).await;
});
}
tokio::time::sleep(tokio::time::Duration::from_secs(5)).await;
}
async fn agent_task(agent_id: usize, tx: mpsc::Sender<ModelUpdate>, seed: u64) {
let mut rng = StdRng::seed_from_u64(seed); // Use a seedable RNG that is Send
loop {
let parameters = vec![rng.gen_range(0.0..1.0); 10];
let update = ModelUpdate { agent_id, parameters };
tx.send(update.clone()).await.unwrap();
println!("Agent {} sent parameters to Central Server", agent_id);
tokio::time::sleep(tokio::time::Duration::from_secs(1)).await;
}
}
The program begins by initializing channels for communication between the central server and agents. The CentralServer struct receives model updates from agents through a shared receiver and distributes aggregated updates to all agents using dedicated sender channels. Each agent runs in its own asynchronous task, generating random model updates using a seedable random number generator (StdRng) to simulate local training. These updates are sent to the central server, which logs the received updates and broadcasts the aggregated parameters back to all agents. The asynchronous design, powered by tokio, allows the server and agents to operate concurrently without blocking, enabling efficient communication and real-time updates.
The code establishes a federated learning environment by defining a ModelUpdate struct to represent messages exchanged between agents and the central server, containing agent IDs and model parameters. The CentralServer struct handles receiving updates from agents, performing parameter aggregation (e.g., averaging), and broadcasting aggregated parameters back to agents. The main function initializes communication channels, spawns the central server as an asynchronous task, and launches individual agents, each running asynchronously. Within the agent task function, agents simulate generating model updates, send them to the central server, receive aggregated parameters, and update their local models, incorporating delays to mimic realistic training intervals. This implementation highlights the use of Rust's tokio and serde for efficient asynchronous communication, demonstrating a scalable and extensible framework for federated learning, with the ModelUpdate struct serving as a flexible foundation for more complex operations.
This implementation illustrates key aspects of FDRL, including decentralized training, aggregation, and communication efficiency. The central server acts as a global aggregator, mimicking the role of a federated learning coordinator, while agents represent individual learning entities with localized models. The use of asynchronous programming models, such as those provided by tokio, highlights the importance of efficient communication in FDRL systems to handle large-scale, distributed environments. Although the simulation uses randomly generated parameters for simplicity, the framework can be extended to incorporate real-world machine learning models and privacy-preserving techniques, making it a robust starting point for building scalable FDRL systems.
Developing a basic FDRL simulation builds upon the federated environment setup by enabling multiple agents to interact with either shared or distributed environments and coordinate their learning processes through decentralized communication. The simulation workflow begins with each agent interacting with its local environment, gathering experiences that are then used to update its policy parameters through local training. Periodically, agents send their updated model parameters to a central server, which aggregates these updates into a global model. This global model is subsequently broadcasted back to the agents, allowing them to synchronize their local policies and leverage collective learning to improve their performance.
In Rust, this simulation can be implemented by extending the federated environment example with additional functionalities that support environment interaction and policy updates. Each agent runs in its own asynchronous task, collecting data, training locally, and communicating with the central server. The central server aggregates the model updates from agents, forming a global policy, and distributes it back to them. This approach demonstrates how Rust's concurrency model, supported by tokio for asynchronous programming and serde for data serialization, facilitates the creation of a collaborative learning system.
The code below implements a simplified FDRL framework where multiple agents asynchronously communicate with a central server to exchange model updates. Each agent performs local training, updates its parameters, and sends these updates to the central server. The central server aggregates the updates, computes the global model, and broadcasts it back to all agents for synchronization. The communication is managed using Rust's tokio library for asynchronous operations and serde for data serialization. This framework demonstrates a collaborative learning setup that can be scaled for distributed systems.
[dependencies]
anyhow = "1.0.93"
tokio = { version = "1.42", features = ["full"] }
serde = { version = "1.0", features = ["derive"] }
rand = { version = "0.8", features = ["std_rng"] }
use tokio::sync::mpsc;
use serde::{Serialize, Deserialize};
use tokio::task;
use std::collections::HashMap;
use rand::rngs::StdRng;
use rand::SeedableRng;
use rand::Rng;
// Define the message structure for parameter updates
#[derive(Serialize, Deserialize, Debug, Clone)]
struct ModelUpdate {
agent_id: usize,
parameters: Vec<f32>, // Simplified parameter representation
}
// Define the central server structure
struct CentralServer {
receiver: mpsc::Receiver<ModelUpdate>,
senders: HashMap<usize, mpsc::Sender<ModelUpdate>>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelUpdate>, senders: HashMap<usize, mpsc::Sender<ModelUpdate>>) -> Self {
CentralServer { receiver, senders }
}
async fn run(&mut self) {
let mut aggregated_parameters: Vec<f32> = Vec::new();
let mut count = 0;
while let Some(update) = self.receiver.recv().await {
println!("Central Server received update from Agent {}", update.agent_id);
if aggregated_parameters.is_empty() {
aggregated_parameters = update.parameters.clone();
} else {
for (i, param) in update.parameters.iter().enumerate() {
aggregated_parameters[i] += param;
}
}
count += 1;
// Once updates from all agents are received, aggregate and broadcast
if count == self.senders.len() {
for param in aggregated_parameters.iter_mut() {
*param /= self.senders.len() as f32;
}
println!("Central Server aggregated parameters: {:?}", aggregated_parameters);
// Broadcast aggregated parameters back to agents
for (&agent_id, sender) in &self.senders {
let message = ModelUpdate {
agent_id,
parameters: aggregated_parameters.clone(),
};
sender.send(message).await.unwrap();
println!("Central Server sent aggregated parameters to Agent {}", agent_id);
}
// Reset for next round
aggregated_parameters = Vec::new();
count = 0;
}
}
}
}
#[tokio::main]
async fn main() {
let num_agents = 3;
// Create channels for agents to send updates to the central server
let (tx, rx) = mpsc::channel(100);
// Create channels for the central server to send updates back to agents
let mut senders_map: HashMap<usize, mpsc::Sender<ModelUpdate>> = HashMap::new();
let mut receivers_map: HashMap<usize, mpsc::Receiver<ModelUpdate>> = HashMap::new();
for id in 0..num_agents {
let (tx_agent, rx_agent) = mpsc::channel(100);
senders_map.insert(id, tx_agent);
receivers_map.insert(id, rx_agent);
}
// Initialize the central server
let mut server = CentralServer::new(rx, senders_map.clone());
// Spawn the central server task
task::spawn(async move {
server.run().await;
});
// Initialize and spawn agent tasks
let mut handles = vec![];
for id in 0..num_agents {
let tx_clone = tx.clone();
let mut rx_agent = receivers_map.remove(&id).unwrap();
let handle = task::spawn(async move {
agent_task(id, tx_clone, &mut rx_agent).await;
});
handles.push(handle);
}
// Wait for all agent tasks to complete
for handle in handles {
handle.await.unwrap();
}
}
// Define a simple agent task
async fn agent_task(agent_id: usize, tx: mpsc::Sender<ModelUpdate>, rx: &mut mpsc::Receiver<ModelUpdate>) {
// Initialize local model parameters randomly with a send-able RNG
let mut rng = StdRng::from_entropy();
let mut parameters: Vec<f32> = (0..10).map(|_| rng.gen_range(0.0..1.0)).collect();
for _ in 0..5 { // Limit number of iterations for demonstration
// Simulate training by updating parameters
for param in parameters.iter_mut() {
*param += rng.gen_range(-0.01..0.01); // Small random updates
}
println!("Agent {} updated parameters: {:?}", agent_id, parameters);
// Send updated parameters to the central server
let update = ModelUpdate { agent_id, parameters: parameters.clone() };
tx.send(update.clone()).await.unwrap();
println!("Agent {} sent parameters to Central Server", agent_id);
// Wait for aggregated parameters from the central server
if let Some(agg_update) = rx.recv().await {
println!("Agent {} received aggregated parameters: {:?}", agent_id, agg_update.parameters);
// Update local model parameters based on aggregated parameters
parameters = agg_update.parameters;
}
// Wait before next update
tokio::time::sleep(tokio::time::Duration::from_secs(1)).await;
}
}
The code implements FDRL system where agents communicate asynchronously with a central server to collaboratively train their models. The ModelUpdate struct defines the structure for updates exchanged between agents and the server, encapsulating the agent's ID and its parameter updates. The CentralServer struct manages this communication, with a receiver to collect updates from agents and senders to distribute aggregated parameters back. Its run method aggregates the updates by averaging and broadcasts the results to all agents. In the main function, communication channels are established, and both the central server and agent tasks are initialized and executed asynchronously. Each agent task simulates training by randomly updating its local parameters, sending these updates to the server, and incorporating the aggregated parameters into its local model upon receipt. Delays are introduced to simulate realistic training cycles, demonstrating how agents and the server collaborate asynchronously to achieve global learning objectives.
This code illustrates fundamental concepts of FDRL, such as decentralized learning, aggregation, and communication efficiency. The asynchronous task-based design ensures scalability by allowing multiple agents and the server to operate concurrently without blocking. The use of parameter aggregation via averaging mirrors real-world federated learning practices, making it applicable for scenarios like edge computing and multi-agent systems. However, the framework can be further enhanced by incorporating techniques like differential privacy for secure parameter exchanges, gradient compression for reducing communication overhead, and weighted aggregation for handling heterogeneous agents. This example serves as a foundational template for building scalable, privacy-preserving FDRL systems in Rust.
To provide a more concrete example, the following Rust code showcases a simplified FDRL application where multiple agents collaboratively train their policies in a federated environment. The FDRL represents a decentralized learning paradigm where multiple agents independently train on local environments and periodically share their model updates with a central server. The central server aggregates these updates and redistributes a unified model to all agents. This approach leverages distributed data while ensuring privacy, as raw data remains on local devices. In the provided code, each Agent simulates a reinforcement learning actor by performing local training and periodically sharing its updated model parameters with a CentralServer for aggregation and redistribution.
[dependencies]
tokio = { version = "1.42", features = ["full"] }
serde = { version = "1.0", features = ["derive"] }
rand = { version = "0.8", features = ["std_rng"] }
tch = "0.12.0"
use tokio::sync::mpsc;
use serde::{Serialize, Deserialize};
use tokio::task;
use std::collections::HashMap;
use tch::{Device, nn};
use rand::Rng;
use tch::nn::OptimizerConfig;
// Define the message structure for parameter updates
#[derive(Serialize, Deserialize, Debug, Clone)]
struct ModelUpdate {
agent_id: usize,
parameters: Vec<f32>, // Simplified parameter representation
}
// Define the central server structure
struct CentralServer {
receiver: mpsc::Receiver<ModelUpdate>,
senders: HashMap<usize, mpsc::Sender<ModelUpdate>>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelUpdate>, senders: HashMap<usize, mpsc::Sender<ModelUpdate>>) -> Self {
CentralServer { receiver, senders }
}
async fn run(&mut self) {
let mut aggregated_parameters: Vec<f32> = Vec::new();
let mut count = 0;
while let Some(update) = self.receiver.recv().await {
println!("Central Server received update from Agent {}", update.agent_id);
if aggregated_parameters.is_empty() {
aggregated_parameters = update.parameters.clone();
} else {
for (i, param) in update.parameters.iter().enumerate() {
aggregated_parameters[i] += param;
}
}
count += 1;
// Once updates from all agents are received, aggregate and broadcast
if count == self.senders.len() {
for param in aggregated_parameters.iter_mut() {
*param /= self.senders.len() as f32;
}
println!("Central Server aggregated parameters: {:?}", aggregated_parameters);
// Broadcast aggregated parameters back to agents
for (&agent_id, sender) in &self.senders {
let message = ModelUpdate {
agent_id,
parameters: aggregated_parameters.clone(),
};
sender.send(message).await.unwrap();
println!("Central Server sent aggregated parameters to Agent {}", agent_id);
}
// Reset for next round
aggregated_parameters = Vec::new();
count = 0;
}
}
}
}
// Define the Agent structure
struct Agent {
id: usize,
receiver: mpsc::Receiver<ModelUpdate>,
sender: mpsc::Sender<ModelUpdate>,
vs: nn::VarStore,
#[allow(dead_code)]
actor: nn::Sequential,
#[allow(dead_code)]
optimizer: nn::Optimizer,
}
impl Agent {
fn new(id: usize, receiver: mpsc::Receiver<ModelUpdate>, sender: mpsc::Sender<ModelUpdate>) -> Self {
// Initialize Variable Store
let vs = nn::VarStore::new(Device::cuda_if_available());
let root = vs.root();
// Define a simple neural network for the Actor
let actor = nn::seq()
.add(nn::linear(&root / "layer1", 4, 128, Default::default()))
.add_fn(|xs| xs.relu())
.add(nn::linear(&root / "layer2", 128, 2, Default::default()))
.add_fn(|xs| xs.tanh()); // Actions are normalized between -1 and 1
let optimizer = nn::Adam::default().build(&vs, 1e-3).unwrap();
Agent { id, receiver, sender, vs, actor, optimizer }
}
async fn run(&mut self) {
loop {
// Simulate local training: update parameters randomly
self.local_training().await;
// Send updated parameters to the central server
let parameters = self.get_parameters();
let update = ModelUpdate { agent_id: self.id, parameters };
self.sender.send(update.clone()).await.unwrap();
println!("Agent {} sent parameters to Central Server", self.id);
// Wait to receive aggregated parameters from the central server
if let Some(agg_update) = self.receiver.recv().await {
println!("Agent {} received aggregated parameters: {:?}", self.id, agg_update.parameters);
self.update_parameters(agg_update.parameters).await;
}
// Wait before next training iteration
tokio::time::sleep(tokio::time::Duration::from_secs(2)).await;
}
}
async fn local_training(&mut self) {
let mut rng = rand::thread_rng();
tch::no_grad(|| {
for mut var in self.vs.variables() {
let delta: f32 = rng.gen_range(-0.01..0.01);
// We create a new tensor and copy the values, avoiding in-place add on a leaf var with grad
let new_val = var.1.f_add_scalar(delta as f64).unwrap();
var.1.copy_(&new_val);
}
});
println!("Agent {} performed local training", self.id);
}
fn get_parameters(&self) -> Vec<f32> {
let mut params = Vec::new();
for (_, var) in self.vs.variables() {
let size = var.size();
let numel: i64 = size.iter().product();
let mut buffer = vec![0f32; numel as usize];
// Convert numel to usize before passing it to copy_data
var.to_device(Device::Cpu).copy_data(&mut buffer, numel as usize);
params.extend(buffer);
}
params
}
async fn update_parameters(&mut self, aggregated_params: Vec<f32>) {
tch::no_grad(|| {
let mut start_idx = 0;
for mut var in self.vs.variables() {
var.1.requires_grad_(false); // Ensure no gradient tracking
// Determine the shape and number of elements for var.1
let shape = var.1.size();
let numel: usize = shape.iter().map(|&dim| dim as usize).product();
if start_idx + numel <= aggregated_params.len() {
// Slice the flattened parameters for this particular variable
let new_tensor_data = &aggregated_params[start_idx..start_idx + numel];
// Create a 1D tensor from the data
let mut new_tensor = tch::Tensor::of_slice(new_tensor_data)
.to_device(tch::Device::cuda_if_available());
// Reshape the tensor using shape as a slice
new_tensor = new_tensor.view(shape.as_slice());
// Now copy is safe since shapes match
var.1.copy_(&new_tensor);
start_idx += numel;
}
}
});
println!("Agent {} updated local parameters with aggregated parameters", self.id);
}
}
#[tokio::main]
async fn main() {
let num_agents = 3;
// Create channels for agents to send updates to the central server
let (tx, rx) = mpsc::channel(100);
// Create channels for the central server to send updates back to agents
let mut senders_map: HashMap<usize, mpsc::Sender<ModelUpdate>> = HashMap::new();
let mut receivers_map: HashMap<usize, mpsc::Receiver<ModelUpdate>> = HashMap::new();
for id in 0..num_agents {
let (tx_agent, rx_agent) = mpsc::channel(100);
senders_map.insert(id, tx_agent);
receivers_map.insert(id, rx_agent);
}
// Initialize the central server
let mut server = CentralServer::new(rx, senders_map.clone());
// Spawn the central server task
task::spawn(async move {
server.run().await;
});
// Initialize and spawn agent tasks
for id in 0..num_agents {
let tx_clone = tx.clone();
let rx_agent = receivers_map.remove(&id).unwrap();
task::spawn(async move {
let mut agent = Agent::new(id, rx_agent, tx_clone);
agent.run().await;
});
}
// Allow some time for communication and training
tokio::time::sleep(tokio::time::Duration::from_secs(20)).await;
}
In this setup, agents train local models independently, using random updates to simulate reinforcement learning dynamics. They send their locally trained model parameters to the CentralServer via asynchronous message channels implemented using tokio::sync::mpsc. The CentralServer aggregates the updates, computes an average, and broadcasts the aggregated parameters back to all agents. The agents incorporate the aggregated parameters into their local models, ensuring convergence towards a globally optimal policy over successive rounds of communication and training. This cycle of local training, aggregation, and redistribution continues iteratively.
The code establishes a federated deep reinforcement learning environment where agents communicate asynchronously with a central server to collaboratively train their models. The ModelUpdate struct defines the format for exchanging parameter updates, including an agent's ID and its parameter vector. The CentralServer struct orchestrates communication by collecting updates via a receiver, aggregating them through averaging, and broadcasting synchronized updates back to agents through its senders. Each Agent has an ID, communication channels, an actor network representing its policy, and an optimizer for local training. The agent's run method manages the learning loop, where local training updates are performed, parameters are sent to the server, and aggregated parameters are received to refine the local model. In the main function, communication channels are initialized, and both the server and agent tasks are executed concurrently using asynchronous programming. Agent tasks mimic realistic training by making small random updates to parameters, exchanging updates with the server, and introducing delays to simulate training intervals, enabling collaborative learning across the system.
The implementation demonstrates the power of tokio for asynchronous communication, enabling scalable and non-blocking operations among agents and the central server. The use of tch for model management allows seamless handling of neural network weights and operations. Key challenges in FDRL include ensuring efficient parameter aggregation, maintaining communication overhead within limits, and addressing issues like model drift due to non-i.i.d data distributions across agents. The provided code serves as a foundational framework for more complex scenarios, such as integrating actual RL environments, reward functions, or advanced optimization strategies.
Federated Deep Reinforcement Learning represents a significant advancement in the field of reinforcement learning, addressing critical challenges related to data privacy, scalability, and decentralized learning. By integrating federated learning principles with reinforcement learning algorithms, FDRL enables the training of intelligent agents in distributed environments without the need for centralized data aggregation. This paradigm is particularly beneficial in applications where data privacy is paramount, computational resources are distributed, and real-time adaptability is essential.
In this introductory section, we explored the foundational aspects of FDRL, including its definition, mathematical framework, and key terminologies. We delved into the importance of FDRL in modern application domains such as edge computing, IoT, and multi-agent systems, highlighting its advantages over traditional centralized reinforcement learning approaches. Furthermore, we addressed the inherent challenges in FDRL, such as data heterogeneity, communication efficiency, privacy concerns, and scalability, providing insights into the complexities that must be navigated to implement effective federated systems.
19.2. Mathematical Foundations of FDRL
Federated Deep Reinforcement Learning (FDRL) represents a powerful synthesis of federated learning and reinforcement learning, creating a framework where multiple agents can collaboratively learn policies while ensuring that sensitive data remains decentralized and private. At its core, FDRL addresses a fundamental challenge in modern AI: how to leverage distributed data and compute resources to train intelligent systems without compromising privacy or efficiency. Imagine a symphony orchestra where individual musicians (agents) practice their parts independently but periodically synchronize with the conductor (global model) to harmonize their efforts. This orchestration ensures both individual growth and collective coherence, much like how FDRL enables decentralized agents to align toward a shared goal.
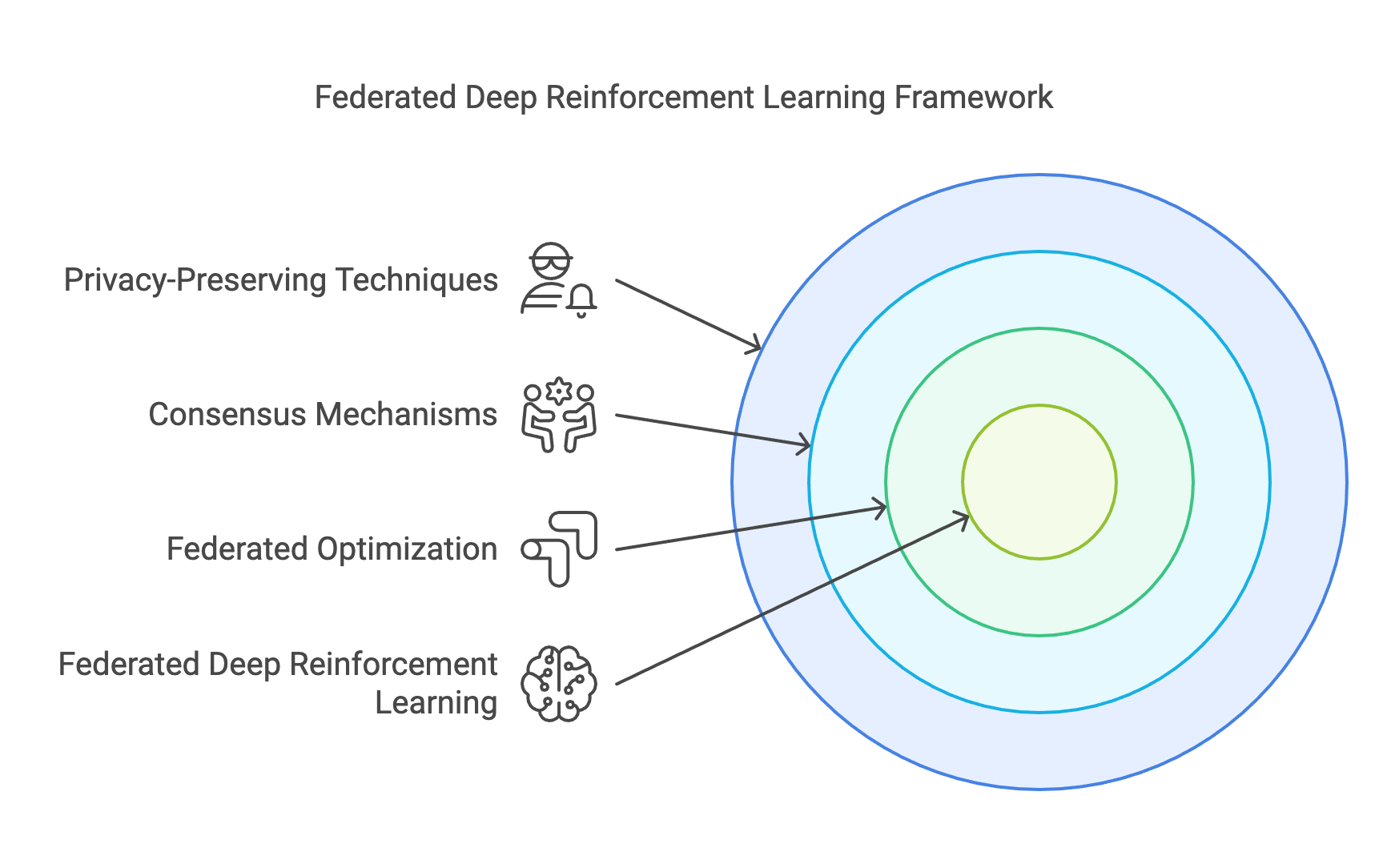
Figure 4: The code framework of FDRL.
The foundation of FDRL is anchored in three critical pillars: federated optimization, consensus mechanisms, and privacy-preserving techniques. Federated optimization serves as the backbone, allowing agents to independently train on local data while periodically sharing updates with a central server or peer network to improve the global policy. This approach eliminates the need for raw data transfer, akin to a decentralized brainstorming session where participants exchange only summaries of their ideas, preserving confidentiality while building on each other's insights.
Consensus mechanisms in FDRL play a vital role in aligning the diverse perspectives of distributed agents. These mechanisms ensure that the updates from individual agents are aggregated into a coherent global model, much like a team agreeing on a common strategy after considering individual contributions. The process must handle differing data distributions, computational capabilities, and even communication delays, making consensus both a technical challenge and a cornerstone of effective collaboration.
Privacy-preserving techniques elevate FDRL's relevance in domains where data sensitivity is paramount. By employing methods like differential privacy and secure multiparty computation, FDRL ensures that individual contributions remain anonymous and secure, even in adversarial settings. Picture a vault where everyone contributes pieces to a puzzle, but no single participant can access the complete picture. This ability to safeguard individual privacy while enabling collective intelligence is one of FDRL's most compelling features.
This section delves into these foundational elements with depth and clarity, offering advanced insights into the practical challenges and trade-offs in federated settings. One significant aspect of FDRL is managing data heterogeneity—when agents operate in environments with vastly different data distributions. Addressing this requires balancing local adaptability with global coherence, much like crafting a quilt where each patch represents unique local patterns yet contributes to a unified design.
At the core of FDRL is the Federated Averaging (FedAvg) algorithm, which facilitates the aggregation of locally trained models into a global model. The mathematical formulation of FedAvg is straightforward yet powerful, leveraging distributed gradient descent with periodic synchronization.
Consider $K$ agents, each with local parameters $\theta_k$ and a local objective function $L_k(\theta)$. The global objective is defined as:
$$L(\theta) = \frac{1}{K} \sum_{k=1}^K L_k(\theta).$$
FedAvg operates by performing local updates at each agent using Stochastic Gradient Descent (SGD):
$$\theta_k^{t+1} = \theta_k^t - \eta \nabla L_k(\theta_k^t),$$
where $\eta$ is the learning rate. Periodically, the central server aggregates these updates to form the global model:
$$\theta^{t+1} = \frac{1}{K} \sum_{k=1}^K \theta_k^{t+1}.$$
In the context of reinforcement learning, $L_k(\theta)$ often corresponds to policy or value function losses derived from local interactions with the environment. FedAvg can be adapted to aggregate policy gradients, enabling distributed policy optimization without sharing raw data.
Consensus mechanisms ensure synchronization among federated agents, facilitating the aggregation of local updates into a coherent global model. A common approach is to model agent interactions as a graph $G = (V, E)$, where $V$ represents the agents, and $E$ denotes the communication links. The update rule for decentralized consensus is:
$$\theta_k^{t+1} = \theta_k^t + \alpha \sum_{j \in \mathcal{N}_k} (\theta_j^t - \theta_k^t),$$
where $\mathcal{N}_k$ is the set of neighbors of agent $k$, and $\alpha$ is the step size. This iterative process aligns local models toward a common consensus, enabling federated optimization without a central server.
In Federated Deep Reinforcement Learning (FDRL), preserving privacy is crucial as agents work with sensitive, localized data. Differential Privacy (DP) is one key technique that protects individual data by introducing noise to gradients or model parameters. This ensures that individual data points cannot be reconstructed from the updates. The noisy parameter update in DP can be expressed as:
$$\theta_k^{t+1} = \theta_k^t - \eta (\nabla L_k(\theta_k^t) + \mathcal{N}(0, \sigma^2)),$$
where $\mathcal{N}(0, \sigma^2)$ is Gaussian noise with variance $\sigma^2$. This mechanism obfuscates specific details while retaining the general utility of the updates. Another technique is Secure Multiparty Computation (SMC), which ensures privacy during model aggregation by distributing the computation across multiple agents. Using methods like additive secret sharing, agents split their updates into shares and only provide partial information for aggregation. This ensures that no single agent gains access to the complete global model or sensitive data, safeguarding the privacy of local information. Together, DP and SMC offer robust solutions for privacy preservation in FDRL systems.
In FDRL, policy learning is inherently distributed. Each agent learns a local policy $\pi_k(a|s; \theta_k)$, which is optimized based on interactions with its local environment. Periodically, these local policies are aggregated to update the global policy:
$$\pi(a|s; \theta) = \frac{1}{K} \sum_{k=1}^K \pi_k(a|s; \theta_k).$$
This approach allows agents to leverage shared knowledge while retaining the flexibility to specialize based on their local environments.
Federated Deep Reinforcement Learning (FDRL) introduces several trade-offs that require careful balancing to optimize performance. One major trade-off lies between communication costs and convergence rates. Frequent communication between agents and the central server accelerates convergence but incurs significant bandwidth overhead. To address this, adaptive communication schedules and model compression techniques can reduce communication frequency while maintaining reasonable convergence speeds. Another trade-off exists between model accuracy and privacy. Adding noise to gradients or parameters to preserve privacy, as in differential privacy, can degrade model accuracy. The challenge is to carefully tune the noise levels to strike a balance between protecting sensitive data and achieving acceptable performance.
Scalability and synchronization also present competing demands. While increasing the number of agents improves scalability and extends the system's capabilities, it complicates synchronization and can slow down convergence. Additionally, handling data heterogeneity poses unique challenges in FDRL, as agents often work with non-IID (non-identically distributed) data, leading to divergent local updates. To address this, weighted aggregation techniques can account for differences in data size across agents. For example, updates can be aggregated as:
$$\theta^{t+1} = \sum_{k=1}^K \frac{n_k}{\sum_{j=1}^K n_j} \theta_k^{t+1},$$
where $n_k$ is the number of samples at agent $k$. Another approach involves introducing regularization terms to align local updates with the global model, such as $L_k(\theta) = L_k(\theta) + \lambda \|\theta - \theta_k^t\|^2$, where $\lambda$ controls the strength of regularization. These strategies help mitigate the effects of data heterogeneity and improve the robustness of FDRL systems.
The Federated Averaging algorithm can be implemented in Rust using asynchronous programming features provided by the tokio crate. Below is a Rust implementation of FedAvg tailored for reinforcement learning agents. The code demonstrates a collaborative learning setup where multiple agents perform localized training on their respective models and communicate with a central server to update and synchronize a shared global model. Each agent operates independently, updating its model using simulated local training dynamics, while the central server aggregates the agents' updates to create a unified global model. This process ensures decentralized training without direct data sharing, maintaining privacy and improving scalability.
[dependencies]
tokio = { version = "1.42", features = ["full"] }
serde = { version = "1.0", features = ["derive"] }
rand = { version = "0.8", features = ["std_rng"] }
use tokio::sync::mpsc;
use serde::{Serialize, Deserialize};
use tokio::task;
use rand::Rng;
use std::collections::HashMap;
// Define the message structure for model updates
#[derive(Serialize, Deserialize, Debug, Clone)]
struct ModelUpdate {
agent_id: usize,
parameters: Vec<f32>,
data_size: usize, // Number of local samples (simulated)
}
// Define the Central Server structure
struct CentralServer {
receiver: mpsc::Receiver<ModelUpdate>,
senders: HashMap<usize, mpsc::Sender<ModelUpdate>>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelUpdate>, senders: HashMap<usize, mpsc::Sender<ModelUpdate>>) -> Self {
CentralServer { receiver, senders }
}
async fn run(&mut self) {
// Initialize a global model with 10 parameters
let param_count = 10;
// Temporary storage for current round of updates
let mut updates: Vec<ModelUpdate> = Vec::new();
while let Some(update) = self.receiver.recv().await {
println!("Central Server received update from Agent {} with data_size: {}", update.agent_id, update.data_size);
// Store the update until we have all agent updates
updates.push(update);
// Once updates from all agents are received, aggregate and broadcast
if updates.len() == self.senders.len() {
// Perform weighted aggregation (FedAvg)
let total_data: usize = updates.iter().map(|u| u.data_size).sum();
// Initialize the aggregated parameters with zeros
let mut global_model = vec![0.0; param_count];
// Weighted sum
for u in &updates {
for (i, &p) in u.parameters.iter().enumerate() {
global_model[i] += p * (u.data_size as f32);
}
}
// Divide by total data to get weighted average
for param in global_model.iter_mut() {
*param /= total_data as f32;
}
println!("Global model updated (FedAvg): {:?}", global_model);
// Broadcast aggregated parameters back to agents
for (&agent_id, sender) in &self.senders {
let message = ModelUpdate {
agent_id,
parameters: global_model.clone(),
data_size: 0, // Not needed when sending global updates
};
sender.send(message).await.unwrap();
println!("Central Server sent global model to Agent {}", agent_id);
}
// Clear updates for next round
updates.clear();
}
}
}
}
// Define the Agent structure
struct Agent {
id: usize,
receiver: mpsc::Receiver<ModelUpdate>,
sender: mpsc::Sender<ModelUpdate>,
local_model: Vec<f32>,
data_size: usize, // Simulated local dataset size
}
impl Agent {
fn new(id: usize, receiver: mpsc::Receiver<ModelUpdate>, sender: mpsc::Sender<ModelUpdate>) -> Self {
let mut rng = rand::thread_rng();
// Initialize a local model with random parameters
let local_model = (0..10).map(|_| rng.gen_range(0.0..1.0)).collect();
// Simulate a data size for the agent. In a real scenario, this
// would represent how many local samples they have.
let data_size = rng.gen_range(50..200);
Agent { id, receiver, sender, local_model, data_size }
}
async fn run(&mut self) {
loop {
self.local_training().await;
// Send updated parameters to the central server, including data_size
let update = ModelUpdate {
agent_id: self.id,
parameters: self.local_model.clone(),
data_size: self.data_size,
};
self.sender.send(update).await.unwrap();
println!("Agent {} sent local model update", self.id);
// Wait to receive aggregated parameters from the central server
if let Some(global_update) = self.receiver.recv().await {
self.local_model = global_update.parameters.clone();
println!("Agent {} updated local model with global model", self.id);
}
tokio::time::sleep(tokio::time::Duration::from_secs(2)).await;
}
}
async fn local_training(&mut self) {
let mut rng = rand::thread_rng();
// Simulate local training by small random perturbations to parameters
for param in self.local_model.iter_mut() {
*param += rng.gen_range(-0.01..0.01);
}
println!("Agent {} performed local training", self.id);
}
}
#[tokio::main]
async fn main() {
let num_agents = 3;
// Create channels for server communication
let (tx, rx) = mpsc::channel(100);
let mut senders: HashMap<usize, mpsc::Sender<ModelUpdate>> = HashMap::new();
let mut receivers: HashMap<usize, mpsc::Receiver<ModelUpdate>> = HashMap::new();
// Create per-agent channels
for id in 0..num_agents {
let (agent_tx, agent_rx) = mpsc::channel(100);
senders.insert(id, agent_tx);
receivers.insert(id, agent_rx);
}
// Initialize and spawn the central server
let mut server = CentralServer::new(rx, senders.clone());
task::spawn(async move {
server.run().await;
});
// Initialize and spawn agent tasks
for id in 0..num_agents {
let sender = tx.clone();
let receiver = receivers.remove(&id).unwrap();
let mut agent = Agent::new(id, receiver, sender);
task::spawn(async move {
agent.run().await;
});
}
// Allow some time for the simulation
tokio::time::sleep(tokio::time::Duration::from_secs(10)).await;
}
The system now operates in iterative cycles that incorporate weighted federated averaging. Agents perform local training, adjusting their model parameters based on simulated updates. These updated parameters, along with the size of the local dataset (data_size), are sent asynchronously to the central server using tokio::sync::mpsc channels. The central server then aggregates these updates by computing a weighted average of the parameters, giving more influence to agents with larger local datasets. After deriving a global model that represents this weighted collective knowledge, the server broadcasts it back to the agents, ensuring all participants remain synchronized. This cyclical process fosters convergence toward a robust, globally beneficial policy.
The code implements a federated deep reinforcement learning (FDRL) simulation that closely mirrors the Federated Averaging (FedAvg) algorithm. The ModelUpdate structure now includes both model parameters and the data_size, encapsulating all the information needed for weighted aggregation. The CentralServer structure collects updates from agents, uses data_size to calculate a weighted average, and forms a global model that it sends back to each agent. Meanwhile, the Agent structure simulates local training and sends model updates tied to its local data size, then incorporates the global model upon receiving it. The main function sets up this entire system, initializing communication channels, spawning the central server as an asynchronous task, and starting multiple agents. As a result, the code supports efficient, concurrent, and asynchronous interactions in a federated environment where agents have varying data workloads.
This FDRL implementation, now incorporating weighted averaging, highlights how asynchronous communication in Rust’s tokio framework can manage complex, concurrent federated learning processes. Although the current setup still simulates training and data distributions, the inclusion of data_size sets the stage for more realistic federated scenarios, where agents hold differently sized datasets and thus have different impacts on the global model. Future enhancements could involve integrating real reinforcement learning tasks, refining communication strategies, and exploring more sophisticated aggregation methods. The resulting framework provides a strong foundation for investigating decentralized learning, accommodating data heterogeneity, and testing scalability in FDRL systems.
This section delved into the mathematical foundations of FDRL, exploring optimization algorithms, consensus mechanisms, and privacy-preserving techniques. The practical implementation of Federated Averaging in Rust highlighted how these concepts translate into actionable code, emphasizing Rust's capabilities for building efficient, scalable, and privacy-aware FDRL systems. As we progress, these foundations will serve as the bedrock for tackling advanced algorithms and real-world applications in federated reinforcement learning.
19.3. Core Algorithms and Paradigms in FDRL
Federated Deep Reinforcement Learning (FDRL) revolutionizes the reinforcement learning paradigm by extending it to decentralized, distributed systems. In traditional reinforcement learning, agents often rely on a centralized framework where data and computational resources converge in a single location. FDRL disrupts this model by empowering multiple agents to independently interact with their local environments, learn optimal policies, and collaboratively contribute to a shared global objective—all while maintaining the confidentiality of their local data. This innovation bridges the growing need for intelligent systems that are both scalable and privacy-preserving, making FDRL a cornerstone of modern AI for distributed applications.
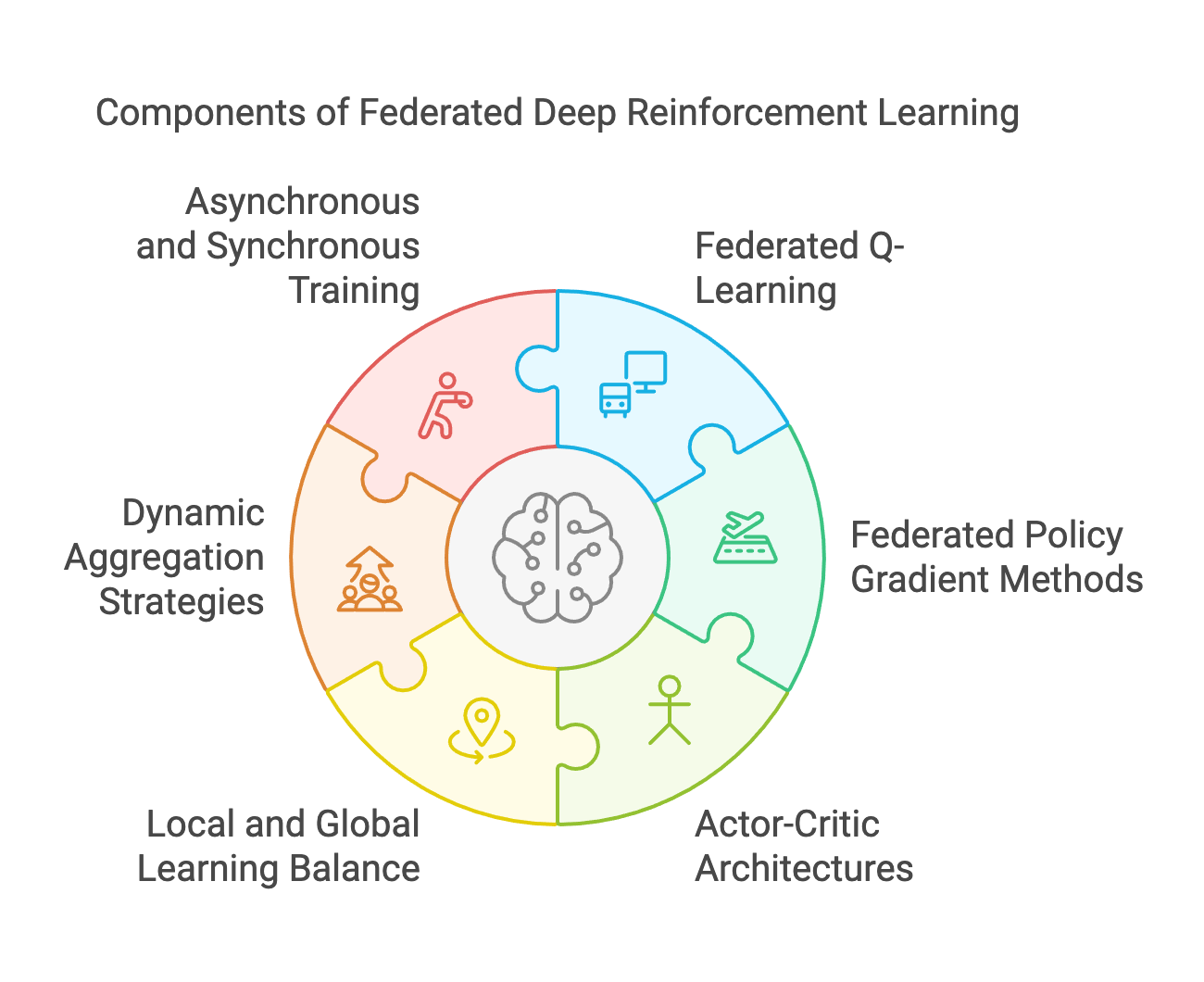
Figure 5: Key components of FDRL model.
At its heart lies the adaptation of traditional reinforcement learning methods to federated settings. Federated Q-Learning brings the classic value-based learning approach into the decentralized domain, allowing agents to independently estimate value functions while periodically synchronizing with a global model. Similarly, Federated Policy Gradient methods refine the policy optimization process for distributed environments, enabling agents to collaboratively improve their policies through gradient aggregation without direct access to others’ data. Building on these approaches, Actor-Critic architectures take center stage in FDRL, combining value-based and policy-based methods to optimize both the policy (actor) and value function (critic) in a federated context. These architectures are particularly well-suited for complex environments, where the interplay between local and global learning objectives demands nuanced coordination.
FDRL also introduces conceptual strategies that address the unique challenges of decentralized learning. Balancing local and global learning is one of the most critical considerations. Each agent must optimize its policy based on localized interactions while ensuring that these updates align with the global model. This balance often requires dynamic aggregation strategies, which weigh individual contributions based on factors like data quality, environment diversity, or computational capabilities. Additionally, the choice between asynchronous and synchronous training paradigms presents another pivotal trade-off. Synchronous training provides consistency by aggregating updates at fixed intervals but risks bottlenecks due to slower agents. Asynchronous training, on the other hand, allows agents to update the global model independently, fostering efficiency but introducing challenges such as stale updates and coordination complexities.
To translate these theoretical concepts into actionable knowledge, this chapter concludes with a comprehensive practical implementation of a Federated Policy Gradient algorithm using Rust. Leveraging the tch-rs crate for tensor operations, the implementation demonstrates how to build robust, scalable FDRL systems that handle distributed learning tasks effectively. Rust’s emphasis on safety, concurrency, and performance makes it an ideal language for such applications, enabling developers to write high-performance code that is both reliable and efficient.
By exploring the intricacies of FDRL algorithms, learning paradigms, and practical implementations, this chapter equips you with the tools to design advanced decentralized learning systems. Whether applied to autonomous vehicles, distributed robotics, or smart infrastructure, FDRL represents a transformative approach to collaborative intelligence, unlocking new possibilities for AI in decentralized, privacy-sensitive domains.
Federated Q-Learning adapts the Q-Learning algorithm to a federated setting, where agents independently update their Q-values based on local experiences while periodically aggregating updates to form a global Q-table.
The standard Q-Learning update rule for an agent $k$ is:
$$Q_k(s, a) \leftarrow Q_k(s, a) + \alpha \left[ r + \gamma \max_{a'} Q_k(s', a') - Q_k(s, a) \right],$$
where:
$s$ and $s'$ are the current and next states,
$a$ and $a'$ are the current and next actions,
$r$ is the reward,
$\alpha$ is the learning rate,
$\gamma$ is the discount factor.
In a federated setting, each agent computes local Q-value updates, and these updates are aggregated periodically to form a global Q-table:
$$Q(s, a) = \frac{1}{K} \sum_{k=1}^K Q_k(s, a).$$
This global Q-table is broadcasted back to agents, ensuring that their local Q-values benefit from the collective learning across all agents.
Policy gradient methods in federated environments optimize policies parameterized by $\theta$ based on the expected return:
$$J(\theta) = \mathbb{E}_{\pi_\theta} \left[ \sum_{t=0}^\infty \gamma^t r_t \right].$$
The gradient of the objective, $\nabla J(\theta)$, is approximated using sampled trajectories:
$$\nabla J(\theta) \approx \frac{1}{T} \sum_{t=0}^T \nabla_\theta \log \pi_\theta(a_t | s_t) R_t,$$
where $R_t$ is the return from time $t$.
In a federated setting, each agent computes local policy gradients:
$$\nabla J_k(\theta) = \frac{1}{T_k} \sum_{t=0}^{T_k} \nabla_\theta \log \pi_\theta(a_t | s_t) R_t.$$
These gradients are aggregated to update a global policy:
$$\theta \leftarrow \theta + \eta \frac{1}{K} \sum_{k=1}^K \nabla J_k(\theta),$$
where $\eta$ is the learning rate.
Actor-Critic methods combine the strengths of policy gradient (actor) and value-based methods (critic). In a federated context, each agent maintains local actor and critic networks:
Actor: $\pi_\theta(a | s)$,
Critic: $V_w(s)$, parameterized by $w$.
The actor’s policy is updated using:
$$\nabla J_k(\theta) = \mathbb{E} \left[ \nabla_\theta \log \pi_\theta(a | s) A_k(s, a) \right],$$
where $A_k(s, a) = r + \gamma V_w(s') - V_w(s)$ is the advantage.
The critic updates its value function parameters www using:
$$w \leftarrow w - \alpha \nabla_w \left( r + \gamma V_w(s') - V_w(s) \right)^2.$$
Periodically, agents share and aggregate their actor and critic parameters to form global updates, facilitating collaborative learning.
Traditional reinforcement learning (RL) algorithms require significant adaptation to function effectively in federated settings, as they must account for decentralized data and the need for efficient aggregation. In federated Q-learning, for instance, local Q-values are periodically aggregated into a global Q-table, enabling distributed learning across multiple agents. Policy gradient methods are adapted by averaging gradients calculated locally by agents, optimizing a shared global policy. Similarly, actor-critic methods in federated settings involve synchronizing actor and critic parameters across agents, a process that must be carefully managed to reduce communication overhead while maintaining model performance.
The FDRL emphasizes a balance between local learning, where agents optimize their policies based on locally observed data, and global learning, which integrates these updates into a unified global model. This balance is achieved through strategies such as weighted aggregation, which considers the volume of data available at each agent, and regularization techniques that align local models with the global policy. Training paradigms in FDRL can be synchronous, where updates are aggregated at fixed intervals to ensure consistency but may result in delays due to slower agents, or asynchronous, where agents update the global model independently, improving efficiency but risking stale updates. These adaptations ensure FDRL systems are both effective and scalable in decentralized environments.
The following Rust implementation demonstrates a federated Actor-Critic algorithm, leveraging the tch-rs crate for tensor operations and tokio for asynchronous communication. In this FDRL, multiple agents, typically located in distributed environments, collaboratively learn a shared policy or value function without directly sharing their local data. This approach is particularly useful in scenarios where privacy, communication efficiency, or data heterogeneity are key concerns, such as in IoT networks, autonomous systems, or healthcare applications. By leveraging the power of DRL for decision-making and federated learning for decentralized training, FDRL allows agents to benefit from collective intelligence while maintaining their autonomy and privacy.
[dependencies]
tokio = { version = "1.42", features = ["full"] }
serde = { version = "1.0", features = ["derive"] }
rand = { version = "0.8", features = ["std_rng"] }
tch = "0.12.0"
use tokio::sync::mpsc;
use tch::{nn};
use serde::{Serialize, Deserialize};
use rand::{Rng, SeedableRng};
use rand::rngs::StdRng;
// Define model parameters for actor and critic
#[derive(Serialize, Deserialize, Clone, Debug)]
struct ModelParams {
actor_params: Vec<f32>,
critic_params: Vec<f32>,
}
// Central server structure for federated aggregation
struct CentralServer {
receiver: mpsc::Receiver<ModelParams>,
senders: Vec<mpsc::Sender<ModelParams>>,
global_actor: Vec<f32>,
global_critic: Vec<f32>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelParams>, senders: Vec<mpsc::Sender<ModelParams>>) -> Self {
let global_actor = vec![0.0; 10]; // Initialize actor parameters
let global_critic = vec![0.0; 10]; // Initialize critic parameters
CentralServer {
receiver,
senders,
global_actor,
global_critic,
}
}
async fn run(&mut self) {
while let Some(params) = self.receiver.recv().await {
// Aggregate actor and critic parameters
for (i, param) in params.actor_params.iter().enumerate() {
self.global_actor[i] += param / self.senders.len() as f32;
}
for (i, param) in params.critic_params.iter().enumerate() {
self.global_critic[i] += param / self.senders.len() as f32;
}
// Broadcast updated global parameters
for sender in &self.senders {
sender.send(ModelParams {
actor_params: self.global_actor.clone(),
critic_params: self.global_critic.clone(),
})
.await
.unwrap();
}
}
}
}
// Define agent structure
struct Agent {
id: usize,
sender: mpsc::Sender<ModelParams>,
receiver: mpsc::Receiver<ModelParams>,
#[allow(dead_code)]
actor: nn::Linear,
#[allow(dead_code)]
critic: nn::Linear,
}
impl Agent {
fn new(
id: usize,
sender: mpsc::Sender<ModelParams>,
receiver: mpsc::Receiver<ModelParams>,
vs: &nn::Path,
) -> Self {
let actor = nn::linear(vs / "actor", 4, 10, Default::default());
let critic = nn::linear(vs / "critic", 4, 10, Default::default());
Agent {
id,
sender,
receiver,
actor,
critic,
}
}
async fn run(&mut self) {
loop {
let mut rng = StdRng::from_entropy();
// Simulate local training
let actor_update: Vec<f32> = (0..10).map(|_| rng.gen_range(-0.01..0.01)).collect();
let critic_update: Vec<f32> = (0..10).map(|_| rng.gen_range(-0.01..0.01)).collect();
drop(rng);
// Send updates to central server
self.sender
.send(ModelParams {
actor_params: actor_update.clone(),
critic_params: critic_update.clone(),
})
.await
.unwrap();
// Receive aggregated parameters
if let Some(_params) = self.receiver.recv().await {
println!("Agent {} updated models with global parameters", self.id);
}
tokio::time::sleep(tokio::time::Duration::from_secs(2)).await;
}
}
}
#[tokio::main]
async fn main() {
let (tx, rx) = mpsc::channel(10);
let mut senders = Vec::new();
let mut receivers = Vec::new();
for _ in 0..3 {
let (agent_tx, agent_rx) = mpsc::channel(10);
senders.push(agent_tx);
receivers.push(agent_rx);
}
let mut server = CentralServer::new(rx, senders.clone());
tokio::spawn(async move {
server.run().await;
});
for (id, receiver) in receivers.into_iter().enumerate() {
let sender = tx.clone();
tokio::spawn(async move {
let vs = nn::VarStore::new(tch::Device::Cpu);
let mut agent = Agent::new(id, sender, receiver, &vs.root());
agent.run().await;
});
}
tokio::time::sleep(tokio::time::Duration::from_secs(10)).await;
}
In this FDRL, each agent independently interacts with its local environment to collect experience and update its local reinforcement learning model, such as a policy network or Q-value function. Periodically, the agents send their model parameters (e.g., gradients or weights) to a central server, which aggregates these updates to create a global model using techniques like weighted averaging. The aggregated global model is then redistributed to the agents, allowing them to align their learning processes while preserving data privacy. The FDRL framework balances the trade-off between local computation and global communication, enabling efficient learning across diverse environments while addressing issues like non-IID data, communication constraints, and privacy requirements.
This simplified FDRL implementation represents a significant step forward in distributed intelligent systems, enabling robust and privacy-preserving collaborative learning across diverse environments. Its decentralized approach allows agents to adapt policies based on heterogeneous experiences, fostering resilience and scalability in dynamic multi-agent systems. However, challenges such as dealing with non-IID data, communication inefficiencies, and adversarial robustness remain open research areas. Despite these hurdles, FDRL holds immense promise for real-world applications, such as autonomous vehicles, personalized healthcare, and smart grids, where cooperative learning under constraints is essential.
This implementation highlights the interplay between local and global learning in a federated Actor-Critic setting, demonstrating the practical application of theoretical concepts in FDRL.
19.4. Communication and Coordination Mechanisms in FDRL
Communication and coordination lie at the heart of Federated Deep Reinforcement Learning (FDRL) systems, serving as the critical glue that binds decentralized agents into a cohesive learning framework. In FDRL, where agents operate across distributed environments, the ability to efficiently exchange, aggregate, and apply model updates is not merely a technical requirement but a fundamental enabler of collaborative intelligence. The decentralized nature of FDRL inherently amplifies the complexity of these interactions, requiring sophisticated communication protocols and coordination strategies to ensure robust and scalable learning systems.
Effective communication in FDRL is not just about transmitting data; it’s about ensuring that these exchanges occur efficiently, securely, and with minimal overhead. Agents often operate in environments with varying computational resources, network bandwidth, and latency. This diversity necessitates adaptive communication protocols that can handle such heterogeneity while maintaining synchronization across the system. Strategies such as gradient compression, sparse updates, and periodic synchronization help reduce bandwidth consumption without compromising model accuracy, much like optimizing a supply chain to ensure timely delivery of essential resources without unnecessary expenditure.
Coordination in FDRL takes this a step further, addressing the dynamic interplay between agents as they contribute to a shared learning objective. The challenge is to aggregate the diverse updates from agents—each influenced by their local environments—into a global model that is representative and actionable. This requires consensus mechanisms that can align individual contributions while mitigating the risks of conflicting updates or adversarial behavior. Robust coordination strategies ensure that the learning system remains stable even as agents drop out, fail, or experience communication disruptions, akin to maintaining harmony in a distributed orchestra where not all musicians may play simultaneously or perfectly.
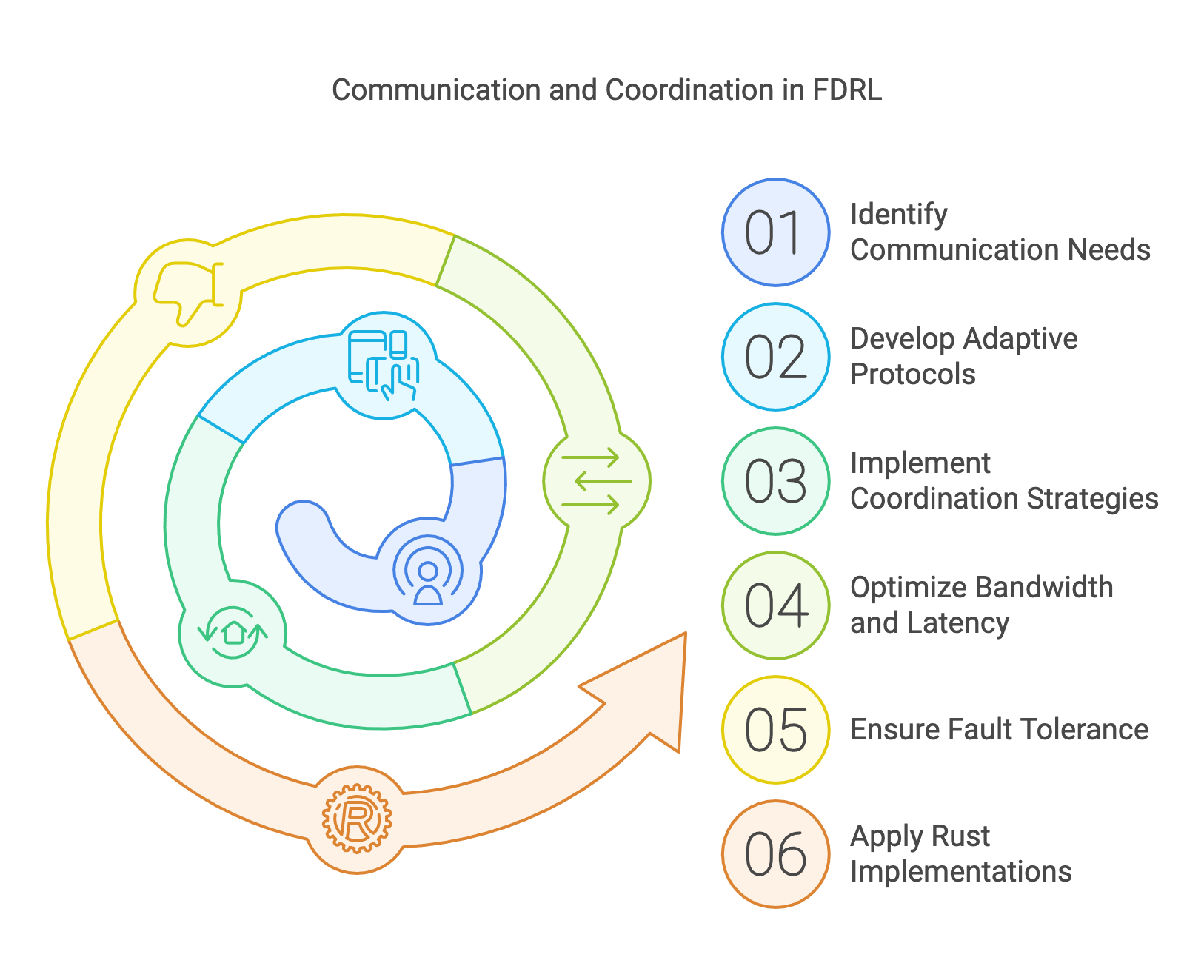
Figure 6: Development process of communication and coordination in FDRL.
This section delves deeply into the intricacies of these communication and coordination mechanisms, presenting advanced techniques for optimizing bandwidth, reducing latency, and ensuring fault tolerance. It examines the trade-offs between synchronous and asynchronous communication paradigms, highlighting their implications for scalability and convergence. Synchronous methods, though reliable, can be bottlenecked by slower agents, whereas asynchronous approaches, while faster, require careful handling of stale updates and potential inconsistencies. Techniques for handling failures and dropouts, such as resilient aggregation algorithms and redundancy in communication channels, are explored to ensure system robustness.
In FDRL, communication protocols govern the exchange of information between agents and the central server or directly among peer agents. These protocols aim to minimize communication overhead while preserving the fidelity of model updates.
Mathematically, let $\theta_k^t$ represent the local parameters of agent $k$ at iteration $t$. The communication protocol determines how these parameters are transmitted and aggregated into a global model $\theta^t$. A simple protocol is periodic aggregation $\theta^t = \frac{1}{K} \sum_{k=1}^K \theta_k^t,$ where $K$ is the number of agents. Advanced protocols may involve sparse updates or compressed representations of $\theta_k^t$, reducing the size of transmitted data.
Bandwidth optimization is a crucial aspect of scaling Federated Deep Reinforcement Learning (FDRL) systems, as it minimizes communication overhead while maintaining learning performance. One effective technique is model compression, which reduces the size of model updates by quantizing parameters to lower precision. For example, parameters can be approximated as $\theta_k^{\text{compressed}} = \text{round}(\theta_k^t \cdot 2^b) / 2^bθ$, where $b$ represents the number of bits used for quantization. Another approach is sparse updates, which transmit only the significant changes in model parameters. These updates can be expressed as $\Delta_k^t = \{ \theta_k^t - \theta_k^{t-1} \mid |\theta_k^t - \theta_k^{t-1}| > \epsilon \}$, where $\epsilon$ is a threshold for sparsity, ensuring only meaningful updates are communicated. Additionally, gradient compression involves transmitting gradients instead of entire models, with techniques like top-$k$ sparsification or random sampling to further reduce data size. These methods collectively enable efficient communication, making FDRL systems more scalable and cost-effective.
Communication delays can significantly impact the convergence and performance of FDRL algorithms. If $d_k$ represents the delay for agent $k$, the global update $\theta^t$ may lag $\theta^t = \frac{1}{K} \sum_{k=1}^K \theta_k^{t-d_k}.$ Asynchronous protocols mitigate this by allowing updates from agents to be aggregated without waiting for all agents:
$$\theta^t = \theta^{t-1} + \eta \frac{1}{K} \sum_{k=1}^K \nabla_k^{t-d_k}.$$
However, they must account for the risk of stale updates degrading learning dynamics.
In centralized communication, a server aggregates updates from agents and broadcasts the global model. This architecture simplifies coordination but introduces a bottleneck at the server and higher latency for agents farther from it.
In decentralized communication, agents exchange updates directly with their peers. This peer-to-peer model enhances scalability and fault tolerance but requires more sophisticated coordination mechanisms, such as consensus algorithms:
$$\theta_k^{t+1} = \theta_k^t + \alpha \sum_{j \in \mathcal{N}_k} (\theta_j^t - \theta_k^t),$$
where $\mathcal{N}_k$ represents the neighbors of agent $k$, and $\alpha$ is the consensus step size.
Effective coordination is crucial for ensuring that updates from multiple agents contribute cohesively toward a unified global policy in federated deep reinforcement learning. One common approach is round-based synchronization, where agents synchronize their updates with the central server at fixed intervals. This method ensures consistency by aligning updates from all agents, but it may introduce delays when some agents require more time to compute their updates.
Another strategy is dynamic weighting, which involves assigning weights to each agent's updates based on factors like data quality or the volume of local data. This approach ensures that agents with more representative or abundant data have a greater influence on the global model, thereby improving overall learning efficiency and fairness.
Prioritized aggregation further enhances coordination by focusing on updates that contribute most significantly to the learning objectives. This strategy allows the system to prioritize critical updates, ensuring faster convergence and improved model performance. Together, these coordination strategies create a robust framework for aligning decentralized updates into a coherent global policy, balancing efficiency and accuracy in federated learning systems.
Federated Deep Reinforcement Learning (FDRL) systems must be designed to handle challenges such as agent dropouts, network failures, and unreliable connections to maintain robust and efficient operation. One effective approach is the use of backup servers, which act as secondary systems capable of taking over the aggregation and coordination tasks if the primary server encounters a failure. This redundancy ensures that the learning process remains uninterrupted and minimizes the risk of data loss or prolonged downtime.
Another critical mechanism is resilient aggregation, which allows the system to proceed with global updates even when some agents are unavailable. By ignoring updates from dropped agents, the system calculates the global model based on the updates received from the active agents. This approach can be formalized as:
$$\theta^t = \frac{1}{|A_t|} \sum_{k \in A_t} \theta_k^t ,$$
where $A_t$ is the set of active agents at time $t$. This strategy prevents stalling and ensures that the system continues to learn effectively, even in scenarios where agent participation fluctuates. Together, these mechanisms enable FDRL systems to remain robust and adaptable in the face of dynamic and unpredictable network conditions.
Using Rust’s tokio crate for asynchronous programming and serde for serialization, we can implement an efficient communication module. The following code demonstrates communication between agents and a central server with error handling for communication failures.
[dependencies]
tokio = { version = "1.42", features = ["full"] }
serde = { version = "1.0", features = ["derive"] }
use tokio::sync::mpsc;
use serde::{Serialize, Deserialize};
use std::collections::HashMap;
// Define the structure for model updates
#[derive(Serialize, Deserialize, Debug, Clone)]
struct ModelUpdate {
agent_id: usize,
parameters: Vec<f32>, // Simplified parameter representation
}
// Central server for communication and aggregation
struct CentralServer {
receiver: mpsc::Receiver<ModelUpdate>,
senders: HashMap<usize, mpsc::Sender<ModelUpdate>>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelUpdate>, senders: HashMap<usize, mpsc::Sender<ModelUpdate>>) -> Self {
CentralServer { receiver, senders }
}
async fn run(&mut self) {
let mut aggregated_params: Vec<f32> = Vec::new();
let mut count = 0;
while let Some(update) = self.receiver.recv().await {
println!("Central Server received update from Agent {}", update.agent_id);
// Aggregate updates
if aggregated_params.is_empty() {
aggregated_params = update.parameters.clone();
} else {
for (i, param) in update.parameters.iter().enumerate() {
aggregated_params[i] += param;
}
}
count += 1;
if count == self.senders.len() {
for param in aggregated_params.iter_mut() {
*param /= self.senders.len() as f32; // Average parameters
}
println!("Global model updated: {:?}", aggregated_params);
// Broadcast global model to agents
for (&agent_id, sender) in &self.senders {
if let Err(e) = sender.send(ModelUpdate {
agent_id,
parameters: aggregated_params.clone(),
}).await {
println!("Failed to send update to Agent {}: {:?}", agent_id, e);
}
}
// Reset for the next round
aggregated_params.clear();
count = 0;
}
}
}
}
// Agent structure for local updates and communication
struct Agent {
id: usize,
sender: mpsc::Sender<ModelUpdate>,
receiver: mpsc::Receiver<ModelUpdate>,
local_params: Vec<f32>,
}
impl Agent {
fn new(id: usize, sender: mpsc::Sender<ModelUpdate>, receiver: mpsc::Receiver<ModelUpdate>) -> Self {
let local_params = vec![0.0; 10]; // Initialize local parameters
Agent {
id,
sender,
receiver,
local_params,
}
}
async fn run(&mut self) {
loop {
// Simulate local parameter updates
for param in self.local_params.iter_mut() {
*param += rand::random::<f32>() * 0.01; // Add small random updates
}
println!("Agent {} updated local parameters", self.id);
// Send local updates to the central server
if let Err(e) = self.sender.send(ModelUpdate {
agent_id: self.id,
parameters: self.local_params.clone(),
}).await {
println!("Failed to send update from Agent {}: {:?}", self.id, e);
}
// Receive global updates
if let Some(global_update) = self.receiver.recv().await {
println!("Agent {} received global update: {:?}", self.id, global_update.parameters);
self.local_params = global_update.parameters.clone();
}
tokio::time::sleep(tokio::time::Duration::from_secs(1)).await;
}
}
}
#[tokio::main]
async fn main() {
let num_agents = 3;
let (tx, rx) = mpsc::channel(100);
let mut senders: HashMap<usize, mpsc::Sender<ModelUpdate>> = HashMap::new();
let mut receivers: HashMap<usize, mpsc::Receiver<ModelUpdate>> = HashMap::new();
// Create communication channels for agents
for id in 0..num_agents {
let (agent_tx, agent_rx) = mpsc::channel(100);
senders.insert(id, agent_tx);
receivers.insert(id, agent_rx);
}
// Initialize the central server
let mut server = CentralServer::new(rx, senders.clone());
tokio::spawn(async move {
server.run().await;
});
// Initialize agents
for id in 0..num_agents {
let sender = tx.clone();
let receiver = receivers.remove(&id).unwrap();
let mut agent = Agent::new(id, sender, receiver);
tokio::spawn(async move {
agent.run().await;
});
}
tokio::time::sleep(tokio::time::Duration::from_secs(10)).await;
}
This code implements a simplified FDRL framework using asynchronous messaging channels (tokio::sync::mpsc) for communication between agents and a central server. Each agent simulates local training by periodically updating its local parameters with small random changes. These updated parameters are sent to the central server, which aggregates updates from all agents. Once updates from all agents are received, the server averages the parameters to produce a global model and broadcasts it back to the agents. Agents then update their local parameters with the global model and continue the cycle. This process ensures decentralized learning while maintaining communication efficiency and data privacy.
The code demonstrates a foundational approach to FDRL, showcasing the key principles of decentralized learning and collaborative intelligence. It highlights the ability of agents to improve their local models using aggregated global knowledge without directly sharing raw data, which is critical for preserving privacy in sensitive applications like healthcare or autonomous systems. However, the simplicity of the model may not handle challenges like non-IID data distributions, communication bottlenecks, or malicious agents effectively. Real-world FDRL systems often require advanced techniques for robust aggregation, fairness, and security to ensure scalability and reliability in diverse environments. This framework serves as a stepping stone toward building such sophisticated systems.
In summary, this section has explored the critical role of communication and coordination in FDRL, discussing mathematical models, optimization techniques, and fault-tolerant strategies. The Rust implementation demonstrated how to design an efficient communication module capable of handling aggregation, bandwidth optimization, and error resilience. These insights and tools form the backbone of scalable, robust FDRL systems, bridging theoretical foundations with real-world applications.
19.5. Privacy and Security in FDRL
Privacy and security are foundational pillars of Federated Deep Reinforcement Learning (FDRL), defining its capacity to function in environments where sensitive data must remain confidential. In an era marked by increasing concerns over data breaches, regulatory constraints, and ethical AI practices, FDRL stands out as a framework designed to prioritize privacy without compromising on collaborative learning. By enabling multiple agents to train a global model while retaining their data locally, FDRL addresses one of the most pressing challenges in artificial intelligence: reconciling the need for data-driven insights with the imperative for data protection.
At the heart of privacy-preserving FDRL are advanced mechanisms such as differential privacy and secure aggregation protocols. Differential privacy ensures that individual contributions from agents remain anonymous, safeguarding against attempts to infer sensitive information from model updates. This technique introduces a layer of noise to the shared data, effectively masking individual details while preserving the statistical utility of the aggregated information. Secure aggregation protocols complement this by enabling agents to collectively compute the global model without revealing their individual inputs, much like contributing puzzle pieces to form a picture without ever disclosing the design of the individual pieces.
Figure 7: Balancing privacy and utility in FDRL implementation.
The importance of privacy in FDRL extends beyond technical safeguards; it is deeply intertwined with trust. For an FDRL system to function effectively, participating agents—whether individuals, organizations, or devices—must trust that their data will not be exposed or misused. This trust is formalized through trust models, which define the relationships and assumptions between agents and the central server (or among peer agents in decentralized systems). Whether the system operates on centralized trust, where a server manages aggregation securely, or decentralized trust, where agents use cryptographic techniques to collaborate directly, the trust model shapes the system’s architecture and security protocols.
Balancing privacy with utility is a nuanced challenge in FDRL. Introducing privacy-preserving techniques, such as noise injection or encryption, can sometimes degrade the performance of the global model. Striking the right balance requires adaptive strategies that dynamically adjust privacy levels based on the sensitivity of the data, the stage of training, and the requirements of the application domain. For instance, in healthcare, preserving patient confidentiality might take precedence over minor reductions in model accuracy, whereas in industrial robotics, performance optimization might hold greater weight.
Equally important is the need for FDRL systems to comply with stringent regulatory frameworks such as GDPR (General Data Protection Regulation) and HIPAA (Health Insurance Portability and Accountability Act). Compliance demands not only the implementation of technical privacy safeguards but also transparency in how data is used, mechanisms for auditing and accountability, and respect for the rights of data owners. Designing FDRL systems that meet these standards ensures not only their legality but also their ethical integrity.
This chapter delves deeply into these aspects, providing both theoretical insights and practical implementations of privacy-preserving techniques in FDRL. We explore mechanisms to mitigate security threats, such as model inversion attacks, where adversaries attempt to reconstruct sensitive data from shared model updates, and poisoning attacks, where malicious agents intentionally introduce corrupt data to degrade the global model. Strategies for resilience, such as anomaly detection, redundant validation, and robust aggregation, are discussed as critical components of a secure FDRL framework.
To bridge theory with application, the chapter includes hands-on Rust implementations of key privacy-preserving techniques. Using Rust’s concurrency and cryptographic libraries, we demonstrate how to implement differential privacy, secure multiparty computation, and fault-tolerant aggregation protocols. These examples highlight Rust’s ability to handle the complexity of secure and efficient distributed systems while providing the performance required for real-world applications.
By balancing advanced privacy mechanisms with practical implementation strategies, this chapter equips you to design FDRL systems that not only respect the confidentiality of individual agents but also achieve robust and reliable performance. Whether applied to sensitive fields like personalized medicine, financial analysis, or collaborative robotics, the principles and tools presented here lay the foundation for secure, ethical, and effective federated learning systems.
Differential Privacy (DP) provides a mathematical guarantee that the inclusion or exclusion of an individual agent's data does not significantly affect the outcome of a computation, thereby protecting sensitive information. In the context of FDRL, differential privacy is applied to the updates shared by agents during training.
The formal definition of differential privacy involves a parameterized privacy budget $\epsilon$. A randomized mechanism $\mathcal{M}$ satisfies $\epsilon$-differential privacy if, for all datasets $D_1$ and $D_2$ differing by at most one entry, and for any subset of outputs $S$:
$$\Pr[\mathcal{M}(D_1) \in S] \leq e^\epsilon \Pr[\mathcal{M}(D_2) \in S].$$
In FDRL, agents add noise $\mathcal{N}(0, \sigma^2)$ to their model updates before sharing them:
$$\theta_k^{\text{private}} = \theta_k + \mathcal{N}(0, \sigma^2),$$
where $\sigma$ is determined based on the desired privacy budget $\epsilon$.
Secure aggregation ensures that the global model is updated without revealing individual agent contributions. This is achieved using cryptographic techniques such as additive secret sharing and homomorphic encryption.
In additive secret sharing, each agent splits its model update $\theta_k$ into $n$ shares:
$$\theta_k = \sum_{i=1}^n \text{Share}_i,$$
and distributes these shares to $n$ other agents. During aggregation, the shares are combined to reconstruct the sum of updates:
$$\sum_{k=1}^K \theta_k = \sum_{i=1}^n \sum_{k=1}^K \text{Share}_{k, i}.$$
This ensures that no single party has access to the full update of any agent.
FDRL systems are vulnerable to several potential security threats that can compromise the integrity and confidentiality of the learning process. One such threat is model inversion attacks, where adversaries exploit the shared model updates to infer sensitive information about the local data of agents. This can lead to privacy breaches, particularly in scenarios where data is highly sensitive, such as healthcare or financial domains. Another challenge is poisoning attacks, where malicious agents deliberately upload incorrect or manipulated updates to the server. This undermines the performance of the global model, potentially steering it toward suboptimal or harmful behaviors. Additionally, eavesdropping poses a significant risk, as unauthorized interception of communications between agents and the central server can lead to leakage of model parameters and other sensitive data.
Mitigating these threats requires a multi-faceted approach. Robust cryptographic protocols such as encryption can secure the communication channels, preventing unauthorized access to transmitted data. Implementing anomaly detection mechanisms allows the system to identify and isolate malicious agents or suspicious updates, preserving the integrity of the global model. Furthermore, ensuring secure communication channels through techniques like Transport Layer Security (TLS) can safeguard interactions between agents and the server, reducing the risk of eavesdropping and tampering. Together, these strategies create a resilient FDRL system capable of maintaining privacy and robustness in adversarial settings.
Adding noise to model updates for differential privacy is crucial for preserving individual data confidentiality in FDRL, but it can also degrade the global model's utility if not handled carefully. To address this trade-off, adaptive noise scaling is often employed, where the level of noise is dynamically adjusted based on the model's convergence state and the sensitivity of the underlying data. This approach ensures that sufficient noise is added to protect privacy without excessively compromising the model's accuracy. Another strategy involves clipping gradients, which limits the magnitude of gradients before adding noise. This prevents outliers from disproportionately influencing the updates, striking a balance between privacy and model utility.
The trust model underlying the federated architecture plays a significant role in shaping security protocols. In centralized trust models, the server is assumed to be trustworthy, and agents securely share their updates with it. This model simplifies aggregation but requires robust measures to secure communications with the server. Conversely, decentralized trust models rely on agents trusting their peers rather than a central authority. In this scenario, consensus protocols are used to aggregate updates, ensuring that no single entity controls the process. Understanding these trust assumptions is critical for designing appropriate privacy-preserving and security mechanisms tailored to the architecture.
FDRL implementations must also adhere to stringent data protection regulations like the General Data Protection Regulation (GDPR) and the California Consumer Privacy Act (CCPA). Compliance requires minimizing data collection and promoting data localization to ensure that sensitive information remains within the originating jurisdiction. Additionally, transparency is key, with organizations expected to provide clear information about data usage and model training processes. Agents should also have mechanisms to audit and control their participation, enabling them to opt out or adjust their level of involvement. These measures ensure that FDRL systems not only protect privacy but also align with ethical and legal standards.
The following Rust code demonstrates how to add noise to model updates for differential privacy using the rand crate.
[dependencies]
rand = { version = "0.8", features = ["std_rng"] }
rand_distr = "0.4.3"
use rand::thread_rng;
use rand_distr::{Distribution, Normal};
// Function to add Gaussian noise for differential privacy
fn add_noise(update: Vec<f32>, noise_std_dev: f32) -> Vec<f32> {
let normal = Normal::new(0.0, noise_std_dev as f64).unwrap(); // Create a Normal distribution
let mut rng = thread_rng();
update
.iter()
.map(|&x| x + normal.sample(&mut rng) as f32)
.collect()
}
fn main() {
let model_update = vec![0.5, 0.8, -0.3, 1.2];
let noise_std_dev = 0.1; // Standard deviation for Gaussian noise
let noisy_update = add_noise(model_update.clone(), noise_std_dev);
println!("Original Update: {:?}", model_update);
println!("Noisy Update: {:?}", noisy_update);
}
The following implementation uses additive secret sharing for secure aggregation.
use rand::Rng;
// Function to split an update into shares
fn split_into_shares(update: Vec<f32>, num_shares: usize) -> Vec<Vec<f32>> {
let mut rng = rand::thread_rng();
let mut shares = vec![vec![0.0; update.len()]; num_shares];
for (i, &value) in update.iter().enumerate() {
let mut sum = 0.0;
for share in shares.iter_mut().take(num_shares - 1) {
share[i] = rng.gen_range(-1.0..1.0);
sum += share[i];
}
shares[num_shares - 1][i] = value - sum;
}
shares
}
// Function to aggregate shares
fn aggregate_shares(shares: Vec<Vec<f32>>) -> Vec<f32> {
let _num_shares = shares.len();
let update_len = shares[0].len();
let mut aggregated = vec![0.0; update_len];
for share in shares {
for (i, &value) in share.iter().enumerate() {
aggregated[i] += value;
}
}
aggregated
}
fn main() {
let model_update = vec![0.5, 0.8, -0.3, 1.2];
let num_shares = 3;
// Split the update into shares
let shares = split_into_shares(model_update.clone(), num_shares);
println!("Shares: {:?}", shares);
// Aggregate the shares
let aggregated_update = aggregate_shares(shares);
println!("Aggregated Update: {:?}", aggregated_update);
assert_eq!(model_update, aggregated_update); // Verify correctness
}
The code implements differential privacy and secure aggregation to enhance the privacy and security of federated deep reinforcement learning. The add_noise function adds Gaussian noise to model updates, using the rand crate's Normal distribution to generate noise, ensuring that individual data points remain confidential. For secure aggregation, the split_into_shares function divides a model update into multiple additive shares, distributing them among agents to prevent any single party from reconstructing the full update. The aggregate_shares function then sums these shares to reconstruct the original update securely. To maintain reliability, the code includes error handling and validation mechanisms that ensure the aggregated update is consistent with the original one, providing both accuracy and robust security in the federated learning process.
In summary, this section addressed the critical aspects of privacy and security in FDRL, combining mathematical rigor with practical implementations. By leveraging differential privacy, secure aggregation protocols, and robust defenses against potential threats, FDRL systems can achieve a balance between data confidentiality and model performance. The Rust implementations provided in this chapter highlight the language's capabilities for building efficient, secure, and privacy-preserving systems in federated environments. As we proceed, these foundations will enable the development of increasingly sophisticated and trustworthy FDRL architectures.
19.6. Scalability and Efficiency in FDRL
Scalability and efficiency are fundamental to the success of Federated Deep Reinforcement Learning (FDRL), where systems often operate in complex, distributed environments with varying numbers of agents, fluctuating communication requirements, and resource constraints. As FDRL applications expand across diverse domains—from coordinating fleets of autonomous vehicles to optimizing smart grid operations—the ability to scale effectively and manage resources efficiently becomes critical. Without robust scalability, the system risks performance bottlenecks, delayed training, and an inability to adapt to growing or changing environments. Similarly, without optimized efficiency, the computational and communication overheads can outweigh the benefits of federated learning, rendering the system impractical for real-world deployment.
Scalability in FDRL involves the system’s capacity to maintain performance as the number of agents increases or the complexity of the environment grows. This requires a careful balance between local computations performed by individual agents and global aggregation processes that integrate their contributions. Distributed computing paradigms play a central role in this balance, allowing computational tasks to be offloaded to edge devices, peer-to-peer networks, or cloud infrastructures. By decentralizing the workload, these paradigms reduce reliance on centralized servers and improve resilience to agent dropouts or network disruptions.
Figure 8: Process to enchange FDRL scalability and efficiency.
Efficiency in FDRL focuses on minimizing resource consumption—such as computational power, memory, and bandwidth—while maintaining effective learning. Strategies for achieving this include reducing the frequency of communication rounds, compressing model updates, and employing asynchronous aggregation techniques to mitigate delays caused by slower agents. These optimizations ensure that even resource-constrained environments, such as IoT networks or remote healthcare facilities, can participate effectively in federated learning.
Adaptive federated learning designs further enhance scalability and efficiency by dynamically adjusting to changing conditions. For instance, systems can use adaptive agent selection to prioritize updates from agents with the most significant contributions or highest-quality data. Similarly, workload distribution can be optimized to balance computational tasks across agents with varying capabilities, preventing bottlenecks caused by underpowered devices. This adaptability ensures that the system remains robust and responsive, even as environmental conditions or agent participation fluctuates.
This section explores these critical elements in detail, introducing metrics for evaluating scalability and strategies for optimizing efficiency. We examine the challenges of handling heterogeneous agents with diverse computational capacities and data distributions, as well as the trade-offs between synchronous and asynchronous training paradigms. Synchronous methods, while consistent and reliable, can be hindered by slow agents or communication delays, whereas asynchronous approaches promote faster updates but require sophisticated mechanisms to handle stale or conflicting contributions.
Scalability in Federated Deep Reinforcement Learning (FDRL) refers to the system's ability to maintain or improve performance as the number of agents, communication rounds, or computational demands increases. Evaluating scalability involves several metrics. Agent scalability measures the maximum number of agents the system can support without significant degradation in convergence or latency. Another key metric is the number of communication rounds required to achieve a certain level of model accuracy, as excessive rounds can hinder efficiency. Computational load, expressed as time complexity $O(T)$, where $T$ represents the number of training steps, reflects the processing requirements per agent and at the central server. For instance, in an FDRL system with $K$ agents, the total communication overhead per round is approximated as $C = K \cdot S$, where $S$ represents the size of the model update sent by each agent. Ensuring scalability requires minimizing $C$ while maintaining robust convergence to achieve system-wide efficiency.
Efficiency in FDRL involves reducing computational and communication costs through innovative strategies. Gradient compression is one approach, transmitting only significant components of gradients, such as the top-$k$ gradients, denoted as $\Delta \theta_k = \text{top}_k(\nabla \theta_k)$. Sparse updates reduce communication frequency by synchronizing only at selected intervals. For example, at every $\tau$-th communication round, the global model update is calculated as $\theta^t = \frac{1}{K} \sum_{k=1}^K \theta_k^t$, while at other rounds, the model remains unchanged at $\theta^{t-1}$. Efficient aggregation techniques, such as hierarchical aggregation, further optimize server-side operations, reducing time complexity to $O(\log K)$. These strategies balance communication and computational costs to enhance system performance.
Resource allocation is another critical component in FDRL, focusing on optimizing the distribution of computational and communication resources among agents. If $R_k$ represents the resources allocated to agent $k$, the objective is to maximize the overall utility of the system while adhering to resource constraints. Mathematically, this is expressed as $\max \sum_{k=1}^K U_k(R_k)$, subject to $\sum_{k=1}^K R_k \leq R_{\text{total}}$, where $U_k(R_k)$ is the utility function of agent $k$, and $R_{\text{total}}$ is the total available resource. Proper allocation ensures that agents can contribute effectively to the global model while avoiding bottlenecks, ultimately improving the scalability and robustness of the FDRL system.
The FDRL can significantly benefit from distributed computing paradigms like edge computing and cloud federation, which enhance scalability and efficiency. In edge computing, agents operate on devices situated near the data source, such as IoT sensors, which minimizes latency and reduces bandwidth requirements. This proximity enables real-time processing and supports environments where immediate actions are critical. In contrast, cloud federation distributes tasks across multiple cloud servers, providing elastic scaling of resources to accommodate varying workloads. This approach ensures that FDRL systems can manage a growing number of agents and increasingly complex computational demands without sacrificing performance or efficiency.
Effective load balancing is essential in FDRL to prevent bottlenecks and maintain uniform task distribution across agents. Dynamic task assignment adapts workloads in real-time, matching computational tasks to each agent's capacity, thereby optimizing resource utilization. Weighted aggregation further enhances load balancing by prioritizing updates from faster or more reliable agents. This technique assigns weights to agent updates based on their computational capacity, represented as $\theta^t = \sum_{k=1}^K w_k \theta_k^t$, where $w_k = \frac{1}{R_k}$, and $R_k$ is the resource availability of agent $k$. By weighting contributions in proportion to their resource efficiency, the system ensures that updates are both timely and impactful.
Adaptive Federated Learning in FDRL introduces flexibility to accommodate resource constraints and varying agent participation. Dynamic agent selection involves choosing a subset of agents for each training round based on available resources, ensuring that only agents capable of contributing effectively participate. This reduces overhead and improves efficiency, particularly in large-scale systems. Elastic synchronization further adapts the system to resource constraints by enabling asynchronous updates, allowing agents to submit updates independently of synchronization intervals. These adaptive techniques ensure that FDRL systems remain scalable and efficient, even in resource-constrained or highly dynamic environments. By integrating these distributed paradigms, load balancing strategies, and adaptive mechanisms, FDRL systems can achieve robust performance and scalability in diverse applications.
Rust’s performance-oriented features, such as zero-cost abstractions, strong type safety, and efficient memory management, make it well-suited for scalable FDRL implementations. The following example demonstrates efficient resource utilization using concurrency primitives.
The following code implements a scalable FDRL framework using tokio for concurrency and rayon for parallel processing.
[dependencies]
tokio = { version = "1.42", features = ["full"] }
serde = { version = "1.0", features = ["derive"] }
rayon = "1.10.0"
use tokio::sync::mpsc;
use rayon::prelude::*;
use serde::{Serialize, Deserialize};
use std::time::Instant;
// Define model update structure
#[derive(Serialize, Deserialize, Clone, Debug)]
struct ModelUpdate {
agent_id: usize,
parameters: Vec<f32>,
}
// Central server for managing updates
struct CentralServer {
receiver: mpsc::Receiver<ModelUpdate>,
senders: Vec<mpsc::Sender<ModelUpdate>>,
global_model: Vec<f32>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelUpdate>, senders: Vec<mpsc::Sender<ModelUpdate>>) -> Self {
let global_model = vec![0.0; 100]; // Initialize global model with 100 parameters
CentralServer {
receiver,
senders,
global_model,
}
}
async fn run(&mut self) {
loop {
let start_time = Instant::now();
// Collect updates from agents
let mut updates: Vec<ModelUpdate> = vec![];
while let Ok(update) = self.receiver.try_recv() {
updates.push(update);
}
// Aggregate updates using parallel processing
self.global_model = self.global_model
.par_iter()
.enumerate()
.map(|(i, ¶m)| {
updates.iter().fold(param, |acc, update| acc + update.parameters[i])
/ updates.len() as f32
})
.collect();
println!("Global model updated: {:?}", &self.global_model[..10]); // Display first 10 params
println!(
"Aggregation completed in {:?}",
Instant::now().duration_since(start_time)
);
// Broadcast global model back to agents
for sender in &self.senders {
let global_update = ModelUpdate {
agent_id: 0,
parameters: self.global_model.clone(),
};
if let Err(e) = sender.send(global_update).await {
println!("Failed to send global update: {:?}", e);
}
}
tokio::time::sleep(tokio::time::Duration::from_secs(2)).await;
}
}
}
// Agent for local training and communication
struct Agent {
id: usize,
sender: mpsc::Sender<ModelUpdate>,
receiver: mpsc::Receiver<ModelUpdate>,
local_model: Vec<f32>,
}
impl Agent {
fn new(id: usize, sender: mpsc::Sender<ModelUpdate>, receiver: mpsc::Receiver<ModelUpdate>) -> Self {
let local_model = vec![0.0; 100]; // Initialize local model
Agent {
id,
sender,
receiver,
local_model,
}
}
async fn run(&mut self) {
loop {
// Simulate local training
for param in self.local_model.iter_mut() {
*param += rand::random::<f32>() * 0.01; // Add small random updates
}
println!("Agent {} updated local model.", self.id);
// Send updates to central server
let update = ModelUpdate {
agent_id: self.id,
parameters: self.local_model.clone(),
};
if let Err(e) = self.sender.send(update).await {
println!("Failed to send update from Agent {}: {:?}", self.id, e);
}
// Receive global model update
if let Some(global_update) = self.receiver.recv().await {
println!(
"Agent {} received global update: {:?}",
self.id, &global_update.parameters[..10]
);
self.local_model = global_update.parameters.clone();
}
tokio::time::sleep(tokio::time::Duration::from_secs(1)).await;
}
}
}
#[tokio::main]
async fn main() {
let num_agents = 5;
let (tx, rx) = mpsc::channel(100);
let mut senders = vec![];
let mut receivers = vec![];
for _ in 0..num_agents {
let (agent_tx, agent_rx) = mpsc::channel(100);
senders.push(agent_tx);
receivers.push(agent_rx);
}
let mut server = CentralServer::new(rx, senders.clone());
tokio::spawn(async move {
server.run().await;
});
for id in 0..num_agents {
let sender = tx.clone();
let receiver = receivers.remove(0);
let mut agent = Agent::new(id, sender, receiver);
tokio::spawn(async move {
agent.run().await;
});
}
tokio::time::sleep(tokio::time::Duration::from_secs(20)).await;
}
The code implements an FDRL system where the central server and agents interact asynchronously and in parallel to maintain an efficient training process. The central server receives model updates from agents through asynchronous communication channels managed by tokio::mpsc. These updates are aggregated in parallel using the rayon crate, enabling scalable and efficient processing of updates even as the number of agents increases. After aggregation, the server broadcasts the updated global model back to the agents, ensuring synchronization across the system. Each agent performs local training by independently updating its model parameters based on its environment and data. These updates are sent to the server, and the agents subsequently synchronize their models with the aggregated global model received from the server. The use of tokio for managing asynchronous tasks ensures that communication between agents and the server is non-blocking, while rayon enables efficient parallel computation during aggregation, demonstrating an optimized combination of concurrency and parallelism for FDRL.
In summary, this section emphasized the importance of scalability and efficiency in FDRL, providing mathematical insights and practical strategies for optimizing resource utilization and handling large-scale multi-agent systems. By leveraging Rust's concurrency primitives and performance features, we demonstrated how to implement scalable FDRL systems capable of adapting to varying computational and communication constraints. As FDRL continues to grow in complexity and application, these techniques will play a critical role in ensuring its practical viability.
19.7. Applications of Federated Deep Reinforcement Learning
Federated Deep Reinforcement Learning (FDRL) represents a groundbreaking paradigm for addressing some of the most intricate and distributed challenges across a wide array of domains, including autonomous vehicles, smart grid management, personalized healthcare, and industrial automation. Its transformative potential lies in its ability to combine decentralized learning principles with reinforcement optimization, empowering multiple agents to collaborate intelligently while preserving the privacy and autonomy of their local environments. By enabling agents to learn collectively without the need for centralized data aggregation, FDRL strikes a crucial balance between collaborative performance and data confidentiality, making it an essential tool for privacy-sensitive, large-scale applications.
FDRL builds upon multi-agent reinforcement learning (MARL) by incorporating the federated learning paradigm, allowing agents to optimize local policies while contributing to a shared global model. This dual focus on local autonomy and global alignment provides a flexible architecture capable of addressing domain-specific challenges such as heterogeneous data distributions, dynamic environments, and resource constraints. For instance, in smart grid management, FDRL enables distributed energy nodes to optimize power allocation locally while collaboratively improving grid-wide efficiency. In autonomous driving, individual vehicles learn traffic navigation strategies that collectively reduce congestion and improve safety, demonstrating how FDRL integrates local and global objectives seamlessly.
A core strength of FDRL is its versatility across diverse domains, each presenting unique challenges and requirements. In healthcare, FDRL facilitates the development of intelligent systems for optimizing patient care protocols while ensuring compliance with privacy regulations like HIPAA and GDPR. In distributed robotics, it enables fleets of robots to coordinate tasks such as warehouse logistics or search-and-rescue operations, overcoming obstacles posed by communication latency and dynamic environments. The chapter explores these application areas in depth, examining how FDRL frameworks adapt to varying constraints and objectives, from minimizing energy consumption in IoT networks to ensuring equitable resource allocation in shared infrastructures.
Integral to the success of FDRL applications is the ability to define and measure performance through domain-specific evaluation metrics. Traditional metrics such as convergence speed and model accuracy are complemented by application-specific benchmarks that reflect real-world goals. For instance, collision rates and fuel efficiency serve as critical metrics in autonomous vehicles, while cost savings and load balancing are key indicators of success in smart grid management. By aligning evaluation criteria with practical outcomes, FDRL ensures its solutions are both impactful and actionable.
The mathematical foundation of FDRL applications relies on Multi-Agent Markov Decision Processes (MMDPs). Consider $K$ agents, each operating in local environments $E_k$. The global environment is modeled as:
$$\mathcal{M} = (\mathcal{S}, \mathcal{A}, \mathcal{T}, \mathcal{R}),$$
where:
$\mathcal{S}$ is the global state space.
$\mathcal{A} = \mathcal{A}_1 \times \mathcal{A}_2 \times \dots \times \mathcal{A}_K$is the joint action space.
$\mathcal{T}$ is the global transition function.
$\mathcal{R}$ is the global reward function.
Each agent $k$ optimizes a local policy $\pi_k(a_k | s)$, with the objective of maximizing a shared global reward:
$$J = \mathbb{E}\left[\sum_{t=0}^\infty \gamma^t \mathcal{R}(s_t, a_t)\right].$$
Formally, these challenges often translate into constraints or additional terms in the reward function:
$$\mathcal{R}(s, a) = r_{\text{task}}(s, a) - \lambda_{\text{privacy}} \|\nabla \theta\|^2,$$
where $r_{\text{task}}$ is the task-specific reward, and $\lambda_{\text{privacy}}$ penalizes violations of privacy constraints.
The FDRL framework adapts seamlessly to domain-specific challenges by addressing unique problems inherent to each application area. In healthcare, FDRL must navigate highly heterogeneous data distributed across multiple hospitals or clinics, where patient demographics, medical equipment, and treatment protocols differ significantly. Furthermore, strict privacy regulations such as HIPAA demand robust mechanisms to ensure that sensitive patient information is never exposed during federated learning. FDRL can offer privacy-preserving model updates and enable collaborative learning between institutions without compromising confidentiality.
In the finance sector, the dynamic and volatile nature of markets presents a unique challenge. Agents, representing trading algorithms or financial decision-makers, must react swiftly to changing conditions while optimizing for long-term gains. Real-time decision-making becomes critical, as delayed updates or poorly synchronized models can lead to significant losses. FDRL addresses these challenges by allowing distributed systems to learn collaboratively, improving model robustness and adaptability in high-stakes environments.
Autonomous systems, such as fleets of autonomous vehicles or robotic swarms, require effective coordination among agents with diverse goals and constraints. These agents must operate in dynamic, shared environments while avoiding conflicts and maximizing overall system efficiency. FDRL facilitates this by enabling decentralized learning, where agents can improve their individual policies while contributing to a global model that aligns their objectives. By addressing these domain-specific challenges, FDRL ensures scalability, efficiency, and robustness in diverse, real-world applications.
Evaluation metrics in Federated Deep Reinforcement Learning (FDRL) are carefully designed to align with the goals and challenges of specific application domains, ensuring that the systems meet practical and domain-specific needs. In healthcare, metrics such as model accuracy, fairness, and improvements in patient outcomes are critical. Accuracy measures the effectiveness of diagnostic or predictive models across diverse patient populations, while fairness ensures equitable performance across different demographic groups. Improvements in patient outcomes, such as reduced hospital readmission rates or better treatment efficacy, highlight the tangible impact of FDRL in real-world healthcare scenarios.
For smart grids, evaluation focuses on metrics like energy efficiency, load balancing, and cost reduction. Energy efficiency measures how effectively the system reduces energy wastage while meeting demand. Load balancing evaluates the system's ability to distribute power resources equitably across the grid, avoiding overloads or failures. Cost reduction captures the economic benefits of optimizing energy production, distribution, and consumption, making FDRL a valuable tool in managing modern energy systems.
In the domain of autonomous vehicles, metrics such as collision rates, travel time, and fuel efficiency play a pivotal role in assessing the system's performance. Low collision rates indicate the safety and reliability of multi-agent coordination, while shorter travel times demonstrate improved route optimization and traffic flow management. Fuel efficiency measures the system's ability to reduce energy consumption, supporting sustainability goals. These tailored evaluation metrics ensure that FDRL implementations are effective, safe, and aligned with the priorities of each specific domain.
FDRL offers transformative solutions across various domains by enabling decentralized agents to collaboratively optimize their objectives while addressing unique challenges. In smart grids, FDRL plays a pivotal role in optimizing energy distribution within decentralized networks. Agents in this system represent nodes like power stations or energy storage units. By dynamically learning to balance energy loads, these agents minimize energy losses and enhance cost savings. The reward function, $\mathcal{R}_{\text{grid}}(s, a) = -\text{Energy Loss} + \text{Cost Savings}$, encapsulates the system's goals, ensuring that energy resources are utilized efficiently while maintaining grid stability.
In autonomous vehicles, FDRL facilitates coordination in complex traffic systems by enabling vehicles to learn policies for essential maneuvers, such as lane changes, speed regulation, and intersection navigation. Each vehicle acts as an agent aiming to reduce travel time and fuel consumption, contributing to smoother traffic flow and lower environmental impact. The reward function, $\mathcal{R}_{\text{traffic}}(s, a) = -\text{Travel Time} - \text{Fuel Consumption}$, ensures that agents prioritize both efficiency and sustainability while navigating dynamic traffic environments.
In distributed robotics, FDRL supports collaborative efforts in tasks like warehouse management or search-and-rescue operations. Here, agents (robots) must coordinate their actions and share information effectively to achieve shared goals. FDRL addresses the inherent challenges of multi-agent coordination, such as communication bottlenecks and conflicting objectives, ensuring that robots work harmoniously in dynamic and often unpredictable environments. By tailoring learning processes to specific tasks and constraints, FDRL enables robots to maximize productivity and adaptability in these critical applications.
Integrating FDRL with real-world systems requires addressing key challenges to ensure seamless operation and compliance. Infrastructure compatibility is essential, as FDRL algorithms must be adaptable to existing hardware and network architectures, often involving edge devices, cloud servers, or IoT networks. Interoperability further demands the design of robust APIs to bridge FDRL systems with domain-specific platforms, enabling smooth integration into sectors like healthcare, finance, or autonomous systems. Additionally, strict adherence to data privacy regulations such as GDPR or HIPAA is paramount when handling sensitive information, ensuring that FDRL implementations not only protect user data but also meet legal and ethical standards across various domains.
The following Rust implementation demonstrates FDRL in a simulated traffic environment, where vehicles learn to coordinate at an intersection.
use tokio::sync::mpsc;
use serde::{Serialize, Deserialize};
use std::time::Duration;
// Define the environment state and action
#[derive(Serialize, Deserialize, Clone, Debug)]
struct TrafficState {
position: f32,
speed: f32,
lane: usize,
}
#[derive(Serialize, Deserialize, Clone, Debug)]
struct TrafficAction {
acceleration: f32,
lane_change: isize,
}
// Model updates exchanged between agents and the server
#[derive(Serialize, Deserialize, Clone, Debug)]
struct ModelUpdate {
agent_id: usize,
parameters: Vec<f32>,
}
// Simulated central server for aggregation
struct CentralServer {
receiver: mpsc::Receiver<ModelUpdate>,
senders: Vec<mpsc::Sender<ModelUpdate>>,
global_model: Vec<f32>,
}
impl CentralServer {
fn new(receiver: mpsc::Receiver<ModelUpdate>, senders: Vec<mpsc::Sender<ModelUpdate>>) -> Self {
let global_model = vec![0.0; 10];
CentralServer {
receiver,
senders,
global_model,
}
}
async fn run(&mut self) {
while let Some(update) = self.receiver.recv().await {
println!("Received update from Agent {}", update.agent_id);
// Aggregate updates (simple averaging)
for (i, param) in update.parameters.iter().enumerate() {
self.global_model[i] += param / self.senders.len() as f32;
}
println!("Global model updated: {:?}", &self.global_model[..5]);
// Broadcast updated model
for sender in &self.senders {
let global_update = ModelUpdate {
agent_id: 0,
parameters: self.global_model.clone(),
};
sender.send(global_update).await.unwrap();
}
tokio::time::sleep(Duration::from_secs(1)).await;
}
}
}
// Vehicle agent learning to navigate traffic
struct VehicleAgent {
id: usize,
local_model: Vec<f32>,
sender: mpsc::Sender<ModelUpdate>,
receiver: mpsc::Receiver<ModelUpdate>,
}
impl VehicleAgent {
fn new(
id: usize,
sender: mpsc::Sender<ModelUpdate>,
receiver: mpsc::Receiver<ModelUpdate>,
) -> Self {
let local_model = vec![0.0; 10];
VehicleAgent {
id,
local_model,
sender,
receiver,
}
}
async fn run(&mut self) {
loop {
// Simulate training by updating local model
for param in self.local_model.iter_mut() {
*param += rand::random::<f32>() * 0.01;
}
println!("Agent {} updated local model.", self.id);
// Send updates to the central server
self.sender
.send(ModelUpdate {
agent_id: self.id,
parameters: self.local_model.clone(),
})
.await
.unwrap();
// Receive global model update
if let Some(update) = self.receiver.recv().await {
println!(
"Agent {} received global update: {:?}",
self.id, &update.parameters[..5]
);
self.local_model = update.parameters;
}
tokio::time::sleep(Duration::from_secs(1)).await;
}
}
}
#[tokio::main]
async fn main() {
let num_agents = 3;
let (tx, rx) = mpsc::channel(100);
let mut senders = vec![];
let mut receivers = vec![];
for _ in 0..num_agents {
let (agent_tx, agent_rx) = mpsc::channel(100);
senders.push(agent_tx);
receivers.push(agent_rx);
}
let mut server = CentralServer::new(rx, senders.clone());
tokio::spawn(async move {
server.run().await;
});
for id in 0..num_agents {
let sender = tx.clone();
let receiver = receivers.remove(0);
let mut agent = VehicleAgent::new(id, sender, receiver);
tokio::spawn(async move {
agent.run().await;
});
}
tokio::time::sleep(Duration::from_secs(10)).await;
}
The code simulates a federated reinforcement learning system for traffic optimization, with key components tailored to model traffic dynamics. The TrafficState and TrafficAction structures encapsulate the state of the traffic system and the actions vehicles can take, such as lane changes or speed adjustments. The CentralServer serves as the coordinator, aggregating policy updates from all vehicles to compute a global model, which is then broadcasted back to the vehicles to maintain synchronization. Each VehicleAgent represents an individual vehicle that learns to navigate traffic by updating its local policy based on the global model received from the central server. This setup enables collaborative learning across multiple vehicles, promoting efficient navigation and reducing congestion in the simulated traffic environment.
In summary, this last section showcased the versatility of FDRL in solving distributed problems across diverse domains. By exploring theoretical frameworks, domain-specific challenges, and real-world integration strategies, we highlighted the breadth of FDRL applications. The practical implementations in Rust demonstrated how FDRL can be applied to coordinate autonomous vehicles and optimize smart grids, emphasizing the importance of scalability, efficiency, and privacy in building robust systems. As these technologies continue to evolve, FDRL stands at the forefront of enabling intelligent, decentralized decision-making at scale.
19.8. Conclusion
Chapter 19 provides a comprehensive exploration of FDRL, bridging theoretical concepts with practical Rust-based implementations. By dissecting the mathematical frameworks, elucidating key algorithms, and demonstrating effective communication and privacy-preserving strategies, the chapter offers a holistic understanding of FDRL. The practical examples and real-world applications underscore Rust's capabilities in handling the intricacies of federated systems, from performance optimization to secure and efficient communication protocols. As artificial intelligence advances towards more collaborative and privacy-conscious paradigms, the insights and techniques presented in this chapter empower readers to harness the full potential of FDRL. Equipped with both the theoretical knowledge and hands-on coding experience, practitioners are well-prepared to design, implement, and innovate within the evolving landscape of decentralized reinforcement learning systems.
19.8.1. Further Learning with GenAI
These prompts are meticulously crafted to guide your exploration and mastery of Federated Deep Reinforcement Learning. By engaging with these advanced topics, you will gain deep theoretical insights, develop sophisticated algorithmic strategies, and acquire practical skills in implementing FDRL models using Rust. This comprehensive approach ensures a well-rounded understanding of FDRL, preparing you to tackle complex, real-world multi-agent learning challenges effectively.
Define Federated Deep Reinforcement Learning (FDRL) and explain how it integrates federated learning with traditional reinforcement learning. Discuss the fundamental principles of FDRL, highlighting the synergy between decentralized data processing and reinforcement learning mechanisms.
Mathematically formulate the distributed optimization problem in FDRL and describe the role of consensus algorithms within this framework. Provide a detailed mathematical overview of how distributed optimization is achieved in FDRL, emphasizing the application of consensus algorithms to ensure coordinated learning across federated agents.
Identify and elaborate on the key terminologies in FDRL, such as federated agents, local and global models, communication protocols, and privacy-preserving techniques. Explain each term in depth, illustrating their interconnections and significance within the FDRL ecosystem.
Compare and contrast Federated Deep Reinforcement Learning with traditional centralized reinforcement learning approaches, highlighting the benefits and limitations of each. Provide a comprehensive comparison, focusing on aspects such as data privacy, computational efficiency, scalability, and convergence properties.
Explain the mathematical foundations of Federated Averaging (FedAvg) and how it is adapted for reinforcement learning in FDRL. Delve into the FedAvg algorithm, detailing its mathematical formulation and modifications required to accommodate the reinforcement learning paradigm within a federated setting.
Describe the consensus mechanisms used in FDRL for aggregating models across federated agents. Provide mathematical formulations and examples. Explore various consensus protocols, their mathematical underpinnings, and how they facilitate coherent model aggregation despite data heterogeneity and communication delays.
Introduce Differential Privacy and Secure Multiparty Computation (SMC) in the context of FDRL. How do these techniques mathematically ensure data privacy? Provide a rigorous mathematical explanation of Differential Privacy and SMC, illustrating their integration into FDRL to safeguard sensitive agent data during federated training.
Discuss the concept of distributed policy learning in FDRL. How are policies learned and updated across distributed agents without centralizing data? Explain the mathematical strategies that enable decentralized policy updates, ensuring that each agent contributes to the global policy while maintaining data locality.
Extend the Q-Learning algorithm to a federated setting. Provide the mathematical formulation and discuss its convergence properties in FDRL. Detail the adaptation of Q-Learning for multiple agents, including how updates are synchronized and aggregated in a federated environment, and analyze the conditions for convergence.
Formulate Policy Gradient methods for decentralized training across multiple agents in FDRL. How do these methods differ from their centralized counterparts? Provide a mathematical description of federated policy gradient algorithms, highlighting the differences in gradient computation and policy updates compared to centralized approaches.
Develop a mathematical model for Actor-Critic architectures within federated environments. How do these models facilitate learning in FDRL? Explain the Actor-Critic framework adapted for FDRL, detailing the mathematical interactions between actors and critics in a distributed setting and their impact on learning efficiency.
Discuss how asynchronous training methods are implemented in FDRL. Provide mathematical strategies to handle asynchronous updates and their implications on model performance. Explore asynchronous training techniques, including mathematical approaches to manage delayed updates and ensure stable convergence despite asynchronous agent interactions.
Mathematically model efficient communication protocols between federated agents and the central server in FDRL. Provide detailed mathematical models of communication protocols, focusing on optimizing bandwidth usage and minimizing latency while ensuring reliable data transmission.
Describe and mathematically formulate model compression techniques used in FDRL to optimize bandwidth. Explain various model compression strategies, such as quantization and sparsification, and provide mathematical formulations demonstrating their effectiveness in reducing communication overhead.
Analyze the impact of communication latency on the convergence and performance of FDRL algorithms. How can latency be mathematically mitigated? Discuss the mathematical relationship between communication delays and learning dynamics, proposing strategies to minimize latency effects and maintain algorithmic performance.
Compare decentralized and centralized communication architectures in FDRL. Provide mathematical insights into their effects on learning dynamics and scalability. Examine the mathematical differences between decentralized and centralized communication setups, analyzing how each architecture influences the scalability and efficiency of FDRL systems.
Define Differential Privacy in the context of FDRL and mathematically demonstrate how it protects agent data during federated learning. Provide a rigorous mathematical definition of Differential Privacy, illustrating its application in FDRL to ensure that individual agent data remains confidential during the training process.
Formulate Secure Aggregation protocols for FDRL. How do these cryptographic techniques mathematically ensure secure model aggregation without revealing individual agent data? Detail the mathematical principles behind Secure Aggregation protocols, explaining how they prevent the disclosure of individual model updates while enabling secure aggregation.
Identify and mathematically model potential attack vectors in FDRL environments, such as model inversion and poisoning attacks. Analyze different types of security threats in FDRL, providing mathematical models that describe how these attacks can compromise the integrity and privacy of the learning process.
Discuss the balance between privacy and utility in FDRL. How can mathematical strategies be employed to maintain model performance while ensuring data privacy? Explore mathematical approaches to achieving an optimal trade-off between maintaining high model accuracy and enforcing strict privacy constraints within FDRL frameworks.
Feel free to utilize these prompts to delve deeper into each aspect of Federated Deep Reinforcement Learning, enhancing both your theoretical knowledge and practical implementation capabilities in Rust.
19.8.2. Hands On Practices
Below are advanced and comprehensive assignments designed to deepen your understanding and practical skills in Federated Deep Reinforcement Learning (FDRL) using Rust. Each assignment is structured to encourage hands-on experimentation, critical thinking, and the application of theoretical knowledge to practical scenarios within FDRL.
Exercise 19.1: Implementing Federated Averaging (FedAvg) for MARL
Task:
Implement the Federated Averaging (FedAvg) algorithm in Rust for a multi-agent reinforcement learning (MARL) system. This implementation should enable multiple federated agents to collaboratively train a shared global policy without centralizing their individual data.
Challenge:
Federated Averaging Mechanism: Develop the FedAvg algorithm that aggregates local policy updates from multiple agents into a global policy. Ensure that the averaging process accounts for varying amounts of data and training iterations across agents.
Distributed Policy Updates: Implement mechanisms for agents to perform local training on their environments and securely send their policy updates to a central server for aggregation.
Concurrency Management: Utilize Rust’s concurrency features (e.g., threads, async/await) to handle simultaneous training and communication among multiple agents efficiently.
Scalability Considerations: Ensure that the FedAvg implementation can scale with an increasing number of agents without significant performance degradation.
Evaluation:
Convergence Analysis: Monitor the convergence of the global policy by tracking cumulative rewards and policy performance across training epochs. Compare the convergence rates of the federated approach against a centralized training baseline.
Communication Efficiency: Assess the bandwidth usage and latency of the FedAvg implementation by measuring the size and frequency of policy update transmissions between agents and the central server.
Policy Performance: Evaluate the effectiveness of the aggregated global policy in various simulated environments (e.g., grid worlds, multi-agent coordination tasks) to ensure that the federated approach maintains or improves performance.
Scalability Testing: Test the FedAvg implementation with different numbers of federated agents to verify its scalability and identify any performance bottlenecks.
Exercise 19.2: Developing Secure Multiparty Computation (SMC) Protocols in Rust for FDRL
Task:
Design and implement Secure Multiparty Computation (SMC) protocols in Rust to ensure secure aggregation of model updates in a Federated Deep Reinforcement Learning (FDRL) system. The goal is to aggregate agents' policy updates without revealing individual agent data to the central server or other agents.
Challenge:
Cryptographic Protocol Design: Develop mathematical formulations of SMC protocols that allow secure aggregation of model updates. Ensure that the protocols prevent any single party from accessing other agents' raw data.
Implementation of SMC in Rust: Utilize Rust’s strong type system and performance capabilities to implement the SMC protocols. Leverage existing Rust crates such as
rust-cryptoorbellmanfor cryptographic operations.Integration with FDRL Pipeline: Seamlessly integrate the SMC protocols with the existing FDRL training pipeline, ensuring that model updates are securely processed and aggregated without data leakage.
Performance Optimization: Optimize the SMC implementation to minimize computational overhead and latency, maintaining the efficiency of the federated training process.
Evaluation:
Security Validation: Conduct rigorous security testing to ensure that the SMC protocols effectively prevent unauthorized access to individual agent data during the aggregation process.
Performance Benchmarking: Measure the computational overhead and latency introduced by the SMC protocols. Compare these metrics against a non-secure aggregation baseline to evaluate the efficiency of the implementation.
Accuracy Assessment: Verify that the secure aggregation process does not degrade the accuracy or performance of the global policy. Ensure that the aggregated model performs comparably to models trained without SMC.
Scalability Testing: Test the SMC protocols with varying numbers of federated agents to assess their scalability and identify potential performance bottlenecks.
Exercise 19.3: Creating a Rust-based Simulation Environment for Federated Policy Gradient Methods
Task:
Develop a comprehensive simulation environment in Rust tailored for testing and validating Federated Policy Gradient methods in FDRL. This environment should support multiple federated agents interacting within a shared or distinct set of environments, facilitating the training and evaluation of federated policy gradient algorithms.
Challenge:
Environment Design: Create modular and extensible environment components that can be easily configured for different multi-agent scenarios (e.g., cooperative games, competitive tasks).
Agent Integration: Implement federated agents capable of performing local policy gradient updates and communicating their gradients to the central server for aggregation.
Policy Gradient Implementation: Develop the core Policy Gradient algorithms (e.g., REINFORCE, Actor-Critic) within the federated framework, ensuring correct computation and synchronization of gradients.
Data Serialization and Communication: Utilize Rust crates like
serdefor efficient data serialization andtokiofor asynchronous communication between agents and the central server.
Evaluation:
Algorithm Validation: Test the federated policy gradient implementation in various simulated environments to verify its correctness and effectiveness in learning optimal policies.
Performance Metrics: Evaluate key performance indicators such as cumulative rewards, policy convergence rates, and computational efficiency across different multi-agent scenarios.
Flexibility Assessment: Assess the simulation environment’s ability to accommodate diverse federated policy gradient methods and multi-agent interactions, ensuring its versatility for future experiments.
Scalability Testing: Measure the environment’s performance with increasing numbers of federated agents and more complex tasks to ensure it can handle large-scale FDRL experiments.
Exercise 19.4: Implementing Differential Privacy in Federated Q-Learning Models in Rust
Task:
Integrate Differential Privacy mechanisms into a Federated Q-Learning model implemented in Rust. The objective is to protect individual agent data while allowing for effective federated training of the Q-Learning algorithm.
Challenge:
Differential Privacy Mechanisms: Develop mathematical formulations for adding noise to Q-value updates to achieve differential privacy guarantees. Choose appropriate noise distributions and scales based on privacy budgets.
Rust Implementation: Implement the noise addition mechanisms in Rust, ensuring that they are correctly applied to the Q-learning updates without introducing significant bias.
Policy Update Integration: Modify the federated Q-Learning pipeline to incorporate differentially private updates, maintaining the balance between privacy protection and learning performance.
Privacy Budget Management: Design strategies to manage and track the cumulative privacy budget across multiple training iterations, preventing excessive privacy loss.
Evaluation:
Privacy Guarantee Validation: Verify that the implemented Differential Privacy mechanisms meet the defined privacy standards (e.g., ε-differential privacy) through theoretical analysis and empirical testing.
Impact on Learning Performance: Assess the effect of noise addition on the accuracy and convergence of the federated Q-Learning model. Compare performance metrics against non-private and differentially private baselines.
Efficiency Assessment: Measure the computational overhead introduced by the Differential Privacy mechanisms, ensuring that the Rust implementation remains efficient.
Scalability Testing: Evaluate the model’s performance and privacy guarantees in environments with varying numbers of federated agents and different levels of data heterogeneity.
Exercise 19.5: Building a Federated Actor-Critic System in Rust for Autonomous Vehicle Coordination
Task:
Design and implement a Federated Actor-Critic system in Rust aimed at coordinating a fleet of autonomous vehicles. This system should enable decentralized training of actor and critic networks while maintaining a shared global policy for efficient vehicle coordination and navigation.
Challenge:
Actor-Critic Architecture Design: Develop separate actor and critic networks for each federated agent (autonomous vehicle), ensuring that the critic networks can incorporate global information during training.
Federated Training Integration: Implement federated training protocols that allow autonomous vehicles to update their local actor and critic networks based on shared global policies while preserving data privacy.
Synchronization Mechanism: Develop synchronization strategies for periodically aggregating local actor and critic updates into global models, leveraging Rust’s concurrency features for efficient communication and processing.
Safety and Coordination: Ensure that the federated actor-critic system prioritizes safety and effective coordination among autonomous vehicles, implementing mechanisms to prevent collisions and optimize traffic flow.
Evaluation:
Coordination Efficiency: Measure the effectiveness of the federated actor-critic system in coordinating multiple autonomous vehicles, focusing on metrics such as collision rates, traffic throughput, and navigation accuracy.
Convergence and Stability: Analyze the convergence behavior and stability of the federated training process by monitoring policy performance and critic accuracy over training epochs.
Privacy Preservation: Assess the system’s ability to maintain data privacy by ensuring that individual vehicle data remains confidential while contributing to the global policy.
Real-World Applicability: Test the federated actor-critic system in simulated autonomous driving environments with varying traffic densities and scenarios to evaluate its robustness and adaptability.
By completing these assignments, you will gain deep insights into advanced Federated Deep Reinforcement Learning concepts, develop practical skills in implementing and optimizing federated models using Rust, and enhance your ability to address the unique challenges associated with decentralized learning systems. These exercises bridge the gap between theoretical understanding and practical application, equipping you to build robust, efficient, and secure FDRL models for real-world applications.
Comments